2021-2022学年人教版数学八年级下册 第十九章 一次函数 复习与检测课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册 第十九章 一次函数 复习与检测课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 673.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 07:27:46 | ||
图片预览








文档简介
(共20张PPT)
19 复习与测试
知识梳理
知识点一:函数的概念
1.常量与变量
常量:数值始终不变的量;
变量:数值发生变化的量
2.函数的概念
一次函数的一般形式为y=kx+b,其中k、b是常数,K≠0.特别地,当b=0时,一次函数即Y=kx(k≠0),是正比例函数.一个x只能对应一个y。
3.自变量的取值范围
1. 一次函数的概念.
函数y=_______(k、b为常数,k______)叫做一次函数. 当b_____时,函数y=____(k____)叫做正比例函数.
kx +b
≠0
=0
≠0
kx
★理解一次函数概念应注意下面两点:
(1)解析式中自变量x的次数是___次,
比例系数_____.
(2)正比例函数是一次函数的特殊形式 .
1
k≠0
知识梳理
2.一次函数与一元一次不等式:
从“数”的角度看
从“形”的角度看
解不等式ax+b>0(a,
b是常数,a≠0) .
x为何值时函数y= ax+b的值大于0.
解不等式ax+b > 0(a,b是常数,a≠0) .
求直线y= ax+b在 x
轴上方的部分(射线)所对应的的横坐标的取值范围.
知识梳理
(1)一次函数y=kx+b(k≠0)的图象是过点
(0,__),(____,0)的__________.
一次函数的图象及性质.
(2)性质:当k>0时, 从左向右上升,即随着x的增大y也增大;
当k<0时, 从左向右下降,即随着 x的增大y反而减小.
b
一条直线
知识梳理
.直线 y=3x+6与x轴的交点的横坐标x的值是方程2x+a=0的解,则a的值是____.
.直线l1: 与直线l2: 在同一平面直角坐标系中,图象如图所示,则关于x的不等式
的解集为 ,方程组
的解为 .
4
x<-2
知识运用
知识梳理
知识点:正比例函数
1.正比例函数的概念
形如y=kx(k≠0)的函数叫做正比例函数
满足条件:①是乘积形式 ②k≠0; ③x的次数是1;
2.正比例函数的图像与性质
图像:正比例函数的图像是一条过原点的直线
性质:当k>0时,正比例函数图像经过一、三象限,y随着x的增大而增大
当k<0时,正比例函数图像经过二、四象限,y随着x的增大而减小
3.待定系数法求正比例函数
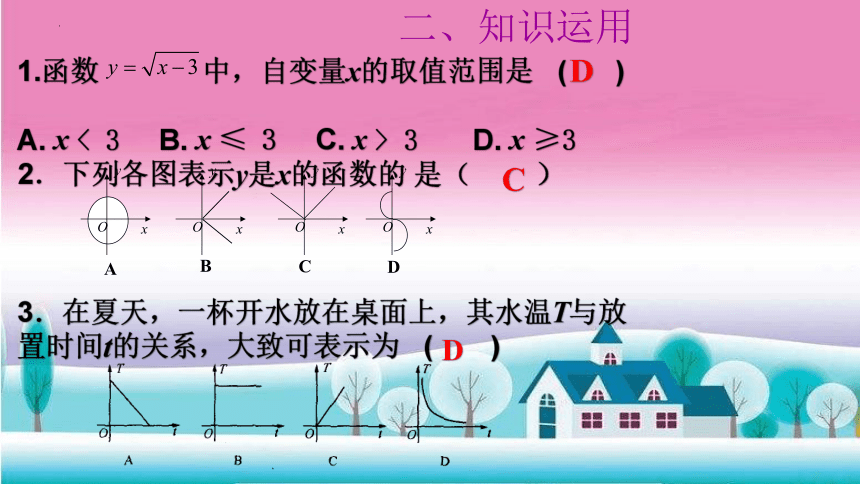
1.函数 中,自变量x的取值范围是 ( )
A. x < 3 B. x ≤ 3 C. x > 3 D. x ≥3
2.下列各图表示y是x的函数的 是( )
3.在夏天,一杯开水放在桌面上,其水温T与放置时间t的关系,大致可表示为 ( )
x
y
O
A
x
y
O
B
x
y
O
D
x
y
O
C
D
C
D
二、知识运用
200
400
104
261.5
450
218
x
y
提问1 :从图上你得到了哪些信息?这些信息对于解决问(1)有什么作用?
重庆市2013年7月1日开始实行电价阶梯收费,如果某居民每月应交电费 y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1)求y与x的函数解析式;
(2)利用函数解析式说明电力公司采用的收费标准;
(3)若某用户7月用电300度,则应缴费多少元?若该用户8月缴费479元,则该用户该月用了多少度电?
O
拓展提高
对应练习
解:(1)由图象可知,当0≤x≤200时,y是x的正比例函数,
设 ,将x=200,y=104代入,
得 ,
所以 ;
当200<x≤400时,设 ,将x=200, x=400,y=218
代入,得 解得 所以y=0.57x-10;
当400<x时,设 , 将x=400,y=218和将x=450,y=261.5代入,
得 解得 , 所以
重庆市2013年7月1日开始实行电价阶梯收费,如果某居民每月应交电费 y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1)求y与x的函数解析式;
(2)利用函数解析式说明电力公司采用的收费标准;
(3)若某用户7月用电300度,则应缴费多少元?若该用户8月缴费479元,则该用户该月用了多少度电?
拓展提高
对应练习
C
如图,在同一直角坐标系中,关于x的一
次函数y = x+ b与 y = bx+1的图象只可能是
( )
x
x
y
O
y
O
O
x
x
y
y
A
B
C
D
C
1.直线 y=2x-12与x轴的交点坐标为( )
A.(6,0) B.(-6,0)
C.(0,6) D.(0,-6)
2.已知一次函数 y=kx+b的图象如图所示,由图象可知,方程kx+b=0的解为 ,不等式kx+b>0的解集为 .
A
x= -1
x<-1
当堂检测
必做题
对应练习
塑料厂某车间生产甲、乙两种塑料的相关信息如下表,请你解答下列问题:
(1)设该车间每月生产甲、乙两种塑料各x吨,利润分别为 元和 元,分别求 和 关于x的函数解析式(注:利润=总收入-总支出);
(2)已知该车间每月生产甲、乙两种塑料均不超过400吨,若某月要生产甲、乙两种塑料共700吨,该月生产甲、乙塑料各多少吨,获得的总利润最大?最大利润是多少?
价
目
品
种
出厂价 成本价 排污处理费
甲种塑料 2100(元/吨) 800(元/吨) 200(元/吨)
乙种塑料 2400(元/吨) 1100(元/吨) 100(元/吨)
每月还需支付设备管理、
维护费20000元
当堂检测
思考题
知识梳理
知识点三:一次函数与一元一次方程
当一次函数y=kx+b的函数值为0时,自变量的值就是一元一次方程kx+b=0的解
(2)已知该车间每月生产甲、乙两种塑料均不超过400吨,若某月要生产甲、乙两种塑料共700吨,该月生产甲、乙塑料各多少吨,获得的总利润最大?最大利润是多少?
出厂价 成本价 排污处理费
甲种塑料 2100(元/吨) 800(元/吨) 200(元/吨)
乙种塑料 2400(元/吨) 1100(元/吨) 100(元/吨)
每月还需支付设备管理、
维护费20000元
解: (2)设该月生产甲种塑料x 吨,则乙种塑料 吨,总利润为W元,依题意得: .
由题意得 解得:
∵ ,∴W随着x的增大而减小,∴当时,W最大=790000(元).
此时, (吨).
因此,生产甲、乙塑料分别为300吨和400吨时总利润最大,最大利润为790000元.
价
目
品
种
通过这节课的复习,你对函数及一次函数有了
哪些新的认识?
在前面学习过程中存在的疑问得到解决了吗?
你还有哪些新的发现?
总结评价
同学们,再见
19 复习与测试
知识梳理
知识点一:函数的概念
1.常量与变量
常量:数值始终不变的量;
变量:数值发生变化的量
2.函数的概念
一次函数的一般形式为y=kx+b,其中k、b是常数,K≠0.特别地,当b=0时,一次函数即Y=kx(k≠0),是正比例函数.一个x只能对应一个y。
3.自变量的取值范围
1. 一次函数的概念.
函数y=_______(k、b为常数,k______)叫做一次函数. 当b_____时,函数y=____(k____)叫做正比例函数.
kx +b
≠0
=0
≠0
kx
★理解一次函数概念应注意下面两点:
(1)解析式中自变量x的次数是___次,
比例系数_____.
(2)正比例函数是一次函数的特殊形式 .
1
k≠0
知识梳理
2.一次函数与一元一次不等式:
从“数”的角度看
从“形”的角度看
解不等式ax+b>0(a,
b是常数,a≠0) .
x为何值时函数y= ax+b的值大于0.
解不等式ax+b > 0(a,b是常数,a≠0) .
求直线y= ax+b在 x
轴上方的部分(射线)所对应的的横坐标的取值范围.
知识梳理
(1)一次函数y=kx+b(k≠0)的图象是过点
(0,__),(____,0)的__________.
一次函数的图象及性质.
(2)性质:当k>0时, 从左向右上升,即随着x的增大y也增大;
当k<0时, 从左向右下降,即随着 x的增大y反而减小.
b
一条直线
知识梳理
.直线 y=3x+6与x轴的交点的横坐标x的值是方程2x+a=0的解,则a的值是____.
.直线l1: 与直线l2: 在同一平面直角坐标系中,图象如图所示,则关于x的不等式
的解集为 ,方程组
的解为 .
4
x<-2
知识运用
知识梳理
知识点:正比例函数
1.正比例函数的概念
形如y=kx(k≠0)的函数叫做正比例函数
满足条件:①是乘积形式 ②k≠0; ③x的次数是1;
2.正比例函数的图像与性质
图像:正比例函数的图像是一条过原点的直线
性质:当k>0时,正比例函数图像经过一、三象限,y随着x的增大而增大
当k<0时,正比例函数图像经过二、四象限,y随着x的增大而减小
3.待定系数法求正比例函数
1.函数 中,自变量x的取值范围是 ( )
A. x < 3 B. x ≤ 3 C. x > 3 D. x ≥3
2.下列各图表示y是x的函数的 是( )
3.在夏天,一杯开水放在桌面上,其水温T与放置时间t的关系,大致可表示为 ( )
x
y
O
A
x
y
O
B
x
y
O
D
x
y
O
C
D
C
D
二、知识运用
200
400
104
261.5
450
218
x
y
提问1 :从图上你得到了哪些信息?这些信息对于解决问(1)有什么作用?
重庆市2013年7月1日开始实行电价阶梯收费,如果某居民每月应交电费 y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1)求y与x的函数解析式;
(2)利用函数解析式说明电力公司采用的收费标准;
(3)若某用户7月用电300度,则应缴费多少元?若该用户8月缴费479元,则该用户该月用了多少度电?
O
拓展提高
对应练习
解:(1)由图象可知,当0≤x≤200时,y是x的正比例函数,
设 ,将x=200,y=104代入,
得 ,
所以 ;
当200<x≤400时,设 ,将x=200, x=400,y=218
代入,得 解得 所以y=0.57x-10;
当400<x时,设 , 将x=400,y=218和将x=450,y=261.5代入,
得 解得 , 所以
重庆市2013年7月1日开始实行电价阶梯收费,如果某居民每月应交电费 y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1)求y与x的函数解析式;
(2)利用函数解析式说明电力公司采用的收费标准;
(3)若某用户7月用电300度,则应缴费多少元?若该用户8月缴费479元,则该用户该月用了多少度电?
拓展提高
对应练习
C
如图,在同一直角坐标系中,关于x的一
次函数y = x+ b与 y = bx+1的图象只可能是
( )
x
x
y
O
y
O
O
x
x
y
y
A
B
C
D
C
1.直线 y=2x-12与x轴的交点坐标为( )
A.(6,0) B.(-6,0)
C.(0,6) D.(0,-6)
2.已知一次函数 y=kx+b的图象如图所示,由图象可知,方程kx+b=0的解为 ,不等式kx+b>0的解集为 .
A
x= -1
x<-1
当堂检测
必做题
对应练习
塑料厂某车间生产甲、乙两种塑料的相关信息如下表,请你解答下列问题:
(1)设该车间每月生产甲、乙两种塑料各x吨,利润分别为 元和 元,分别求 和 关于x的函数解析式(注:利润=总收入-总支出);
(2)已知该车间每月生产甲、乙两种塑料均不超过400吨,若某月要生产甲、乙两种塑料共700吨,该月生产甲、乙塑料各多少吨,获得的总利润最大?最大利润是多少?
价
目
品
种
出厂价 成本价 排污处理费
甲种塑料 2100(元/吨) 800(元/吨) 200(元/吨)
乙种塑料 2400(元/吨) 1100(元/吨) 100(元/吨)
每月还需支付设备管理、
维护费20000元
当堂检测
思考题
知识梳理
知识点三:一次函数与一元一次方程
当一次函数y=kx+b的函数值为0时,自变量的值就是一元一次方程kx+b=0的解
(2)已知该车间每月生产甲、乙两种塑料均不超过400吨,若某月要生产甲、乙两种塑料共700吨,该月生产甲、乙塑料各多少吨,获得的总利润最大?最大利润是多少?
出厂价 成本价 排污处理费
甲种塑料 2100(元/吨) 800(元/吨) 200(元/吨)
乙种塑料 2400(元/吨) 1100(元/吨) 100(元/吨)
每月还需支付设备管理、
维护费20000元
解: (2)设该月生产甲种塑料x 吨,则乙种塑料 吨,总利润为W元,依题意得: .
由题意得 解得:
∵ ,∴W随着x的增大而减小,∴当时,W最大=790000(元).
此时, (吨).
因此,生产甲、乙塑料分别为300吨和400吨时总利润最大,最大利润为790000元.
价
目
品
种
通过这节课的复习,你对函数及一次函数有了
哪些新的认识?
在前面学习过程中存在的疑问得到解决了吗?
你还有哪些新的发现?
总结评价
同学们,再见
