17-1勾股定理课件人教版数学八年级下册(共21张PPT)
文档属性
| 名称 | 17-1勾股定理课件人教版数学八年级下册(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 16:56:56 | ||
图片预览






文档简介
(共21张PPT)
17.1 勾股定理
学习目标
学习目标
1、学习勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2、培养在实际生活中发现问题总结规律的意识和能力。
重点
理解勾股定理的证明方法。
难点
会用面积法证明勾股定理。
A
B
C
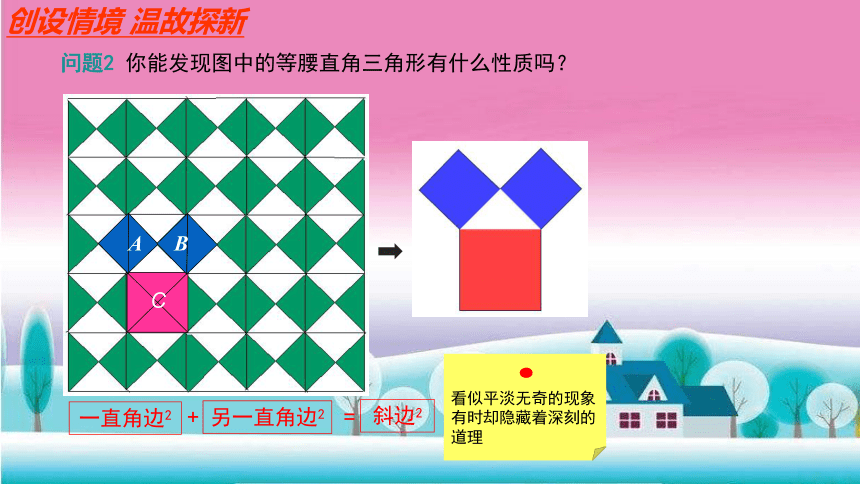
问题2 你能发现图中的等腰直角三角形有什么性质吗?
一直角边2
另一直角边2
斜边2
+
=
看似平淡无奇的现象有时却隐藏着深刻的道理
创设情境 温故探新
赵爽
拼一拼 请同学们准备四个完全相同的直角三角形,跟着我国汉代数学家赵爽拼图.
勾股定理的验证
二
合作交流探究新知
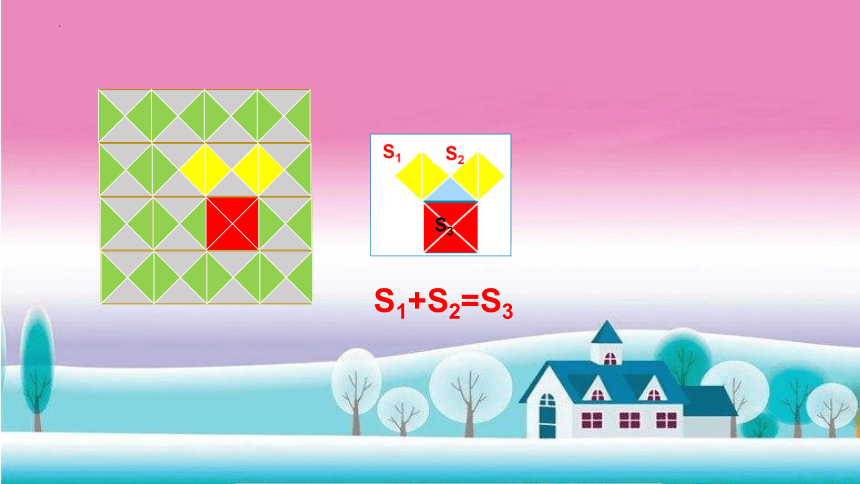
S1+S2=S3
探索与思考(利用补全面积法)
等腰直角三角形有这个性质,其它直角三角形是否也具有这样的性质?
A
B
C
SA =4×4=16
SB =6×6=36
SC (补全法)=10×10 - 4× ×4 ×6=52
SA + SB =SC
直角三角形两直角边的平方和等于斜边的平方。
进一步思考
是不是直角边不一样长的直角三角形都遵循这个规律呢?
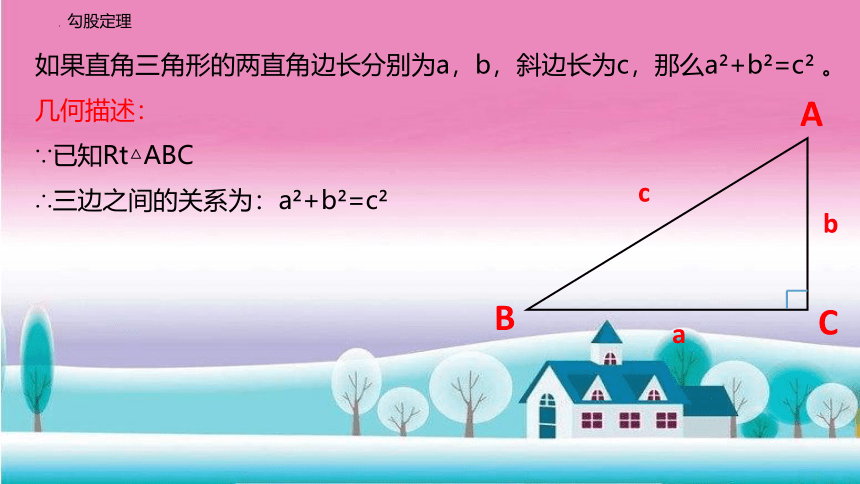
勾股定理
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a +b =c 。
几何描述:
∵已知Rt△ABC
∴三边之间的关系为:a +b =c
b
a
c
A
B
C
赵爽所用的这种方法是我国古代常用的“出入相补法”.在西方,人们称勾股定理为毕达哥拉斯定理.
赵爽弦图
c
b
a
黄
实
朱实
2000多年来,人们对勾股定理的证明颇感兴趣,不但因为这个定理重要、基本,还因为这个定理贴近人们的生活实际.以至于古往今来,上至帝王总统都愿意探讨、研究它的证明,新的证法不断出现.建议同学们课外认真阅读P30《勾股定理的证明》.
合作交流探究新知
C
B
C
A
“割”的方法
3
4
SC = 4×S小直角三角形 + S小正方形
小组讨论
请利用下面的全等直角三角形的图示摆放,根据图示的边长,选择其中一个图形,分析其面积关系后证明猜想,并与同学交流过程。
例2 已知:Rt△ABC中,AB=4,AC=3,则BC= .
5 或
4
3
A
C
B
4
3
C
A
B
温馨提示 当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下,一定要进行分类讨论,否则容易丢解.
范例研讨运用新知
(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
继续思考
A
B
C
C
B
A
在这些直角三角形中,两条直角边的平方和,等于斜边的平方.
2002国际数学会徽------赵爽弦图
切割
拼接
面积关系
勾股定理
探索勾股定理的证明过程
“赵爽弦图”巧妙的利用面积关系证明了勾股定理,是我国古代数学的骄傲,如下图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长的直角边长为,较短的直角边长为,若,大正方形的面积为,则小正方形的面积为__________.
【详解】解:如图所示:
∵ ,∴ ,
∵大正方形的面积为,
∴2ab=21-13=8,∴小正方形的面积为13- =13-2ab=13-8=5.
故答案为:5.
新课导入
提问
这节课我们就来学习用勾股定理解决实际问题.
利用勾股定理求直角三角形第三边长
在中,,,,则( )
A.4 B.3 C.2 D.1
【详解】
解:∵中,∠C=90°,且AB=5,BC=3,
∴AC==4.
故选:A.
观察
1.木板能横着或竖着从门框通过吗?
2.这个门框能通过的最大长度是多少?
不能
3.怎样判定这块木板能否通过木框?
求出斜边的长,与木板的宽比较.
勾股定理是初中阶段非常重要的定理,它是数形结合的典型体现。分析折叠问题中的图形,在复杂的图形中抽取基本图形,建立直角三角形模型,寻找恰当的等量关系式,利用勾股定理建立方程解决问题。
勾股定理
内容
在Rt △ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
课堂小结
同学们,再见
17.1 勾股定理
学习目标
学习目标
1、学习勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2、培养在实际生活中发现问题总结规律的意识和能力。
重点
理解勾股定理的证明方法。
难点
会用面积法证明勾股定理。
A
B
C
问题2 你能发现图中的等腰直角三角形有什么性质吗?
一直角边2
另一直角边2
斜边2
+
=
看似平淡无奇的现象有时却隐藏着深刻的道理
创设情境 温故探新
赵爽
拼一拼 请同学们准备四个完全相同的直角三角形,跟着我国汉代数学家赵爽拼图.
勾股定理的验证
二
合作交流探究新知
S1+S2=S3
探索与思考(利用补全面积法)
等腰直角三角形有这个性质,其它直角三角形是否也具有这样的性质?
A
B
C
SA =4×4=16
SB =6×6=36
SC (补全法)=10×10 - 4× ×4 ×6=52
SA + SB =SC
直角三角形两直角边的平方和等于斜边的平方。
进一步思考
是不是直角边不一样长的直角三角形都遵循这个规律呢?
勾股定理
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a +b =c 。
几何描述:
∵已知Rt△ABC
∴三边之间的关系为:a +b =c
b
a
c
A
B
C
赵爽所用的这种方法是我国古代常用的“出入相补法”.在西方,人们称勾股定理为毕达哥拉斯定理.
赵爽弦图
c
b
a
黄
实
朱实
2000多年来,人们对勾股定理的证明颇感兴趣,不但因为这个定理重要、基本,还因为这个定理贴近人们的生活实际.以至于古往今来,上至帝王总统都愿意探讨、研究它的证明,新的证法不断出现.建议同学们课外认真阅读P30《勾股定理的证明》.
合作交流探究新知
C
B
C
A
“割”的方法
3
4
SC = 4×S小直角三角形 + S小正方形
小组讨论
请利用下面的全等直角三角形的图示摆放,根据图示的边长,选择其中一个图形,分析其面积关系后证明猜想,并与同学交流过程。
例2 已知:Rt△ABC中,AB=4,AC=3,则BC= .
5 或
4
3
A
C
B
4
3
C
A
B
温馨提示 当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下,一定要进行分类讨论,否则容易丢解.
范例研讨运用新知
(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
继续思考
A
B
C
C
B
A
在这些直角三角形中,两条直角边的平方和,等于斜边的平方.
2002国际数学会徽------赵爽弦图
切割
拼接
面积关系
勾股定理
探索勾股定理的证明过程
“赵爽弦图”巧妙的利用面积关系证明了勾股定理,是我国古代数学的骄傲,如下图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长的直角边长为,较短的直角边长为,若,大正方形的面积为,则小正方形的面积为__________.
【详解】解:如图所示:
∵ ,∴ ,
∵大正方形的面积为,
∴2ab=21-13=8,∴小正方形的面积为13- =13-2ab=13-8=5.
故答案为:5.
新课导入
提问
这节课我们就来学习用勾股定理解决实际问题.
利用勾股定理求直角三角形第三边长
在中,,,,则( )
A.4 B.3 C.2 D.1
【详解】
解:∵中,∠C=90°,且AB=5,BC=3,
∴AC==4.
故选:A.
观察
1.木板能横着或竖着从门框通过吗?
2.这个门框能通过的最大长度是多少?
不能
3.怎样判定这块木板能否通过木框?
求出斜边的长,与木板的宽比较.
勾股定理是初中阶段非常重要的定理,它是数形结合的典型体现。分析折叠问题中的图形,在复杂的图形中抽取基本图形,建立直角三角形模型,寻找恰当的等量关系式,利用勾股定理建立方程解决问题。
勾股定理
内容
在Rt △ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
课堂小结
同学们,再见
