18-1-2平行四边形的判定课件人教版数学八年级下册(共21张PPT)
文档属性
| 名称 | 18-1-2平行四边形的判定课件人教版数学八年级下册(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 582.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 17:04:39 | ||
图片预览






文档简介
(共21张PPT)
18.1.2 平行四边形的判定
探索与思考
A
B
D
C
平行四边形的性质:
平行四边形对边相等
平行四边形对角线互相平分
根据逆命题内容,尝试依次画出四边形,它们是平行四边形吗?
平行四边形对角相等
平行四边形性质的逆命题:
两组对边分别相等的四边形是平行四边形。
两组对角分别相等的四边形是平行四边形。
对角线互相平分的四边形是平行四边形。
从教格言
让学生在轻松、快乐的氛围中成就梦想!
工人师傅在施工过程中不小心打破了一块平行四边形玻璃,刚好有两边是完好的,请同学们帮帮忙,有没有办法还原平行四边形?
A
B
C
小问题大学问
导 入 新 课
猜想:
两组对边分别相等的四边形是平行四边形.
探索平行四边形的判定条件
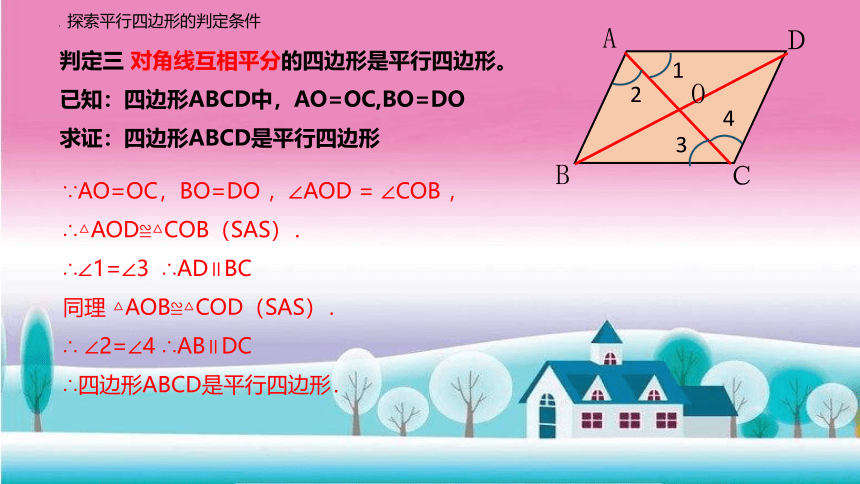
判定三 对角线互相平分的四边形是平行四边形。
已知:四边形ABCD中,AO=OC,BO=DO
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
O
∵AO=OC,BO=DO ,∠AOD = ∠COB ,
∴△AOD≌△COB(SAS).
∴∠1=∠3 ∴AD∥BC
同理 △AOB≌△COD(SAS).
∴ ∠2=∠4 ∴AB∥DC
∴四边形ABCD是平行四边形.
已知:如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
证明:如图,连接AC,
∵AB∥CD,
∴∠1=∠ .
又AB=CD,AC=CA,
∴△ABC≌ ( )
∴BC= ( )
∴四边形ABCD是平行四边形.( )
A
D
B
C
1
2
△CDA
SAS
AD
全等三角形的对应边相等
你还有其它证法吗?
A
D
B
C
1
2
o
探究新知
两组对边分别相等的四边形是平行四边形
2
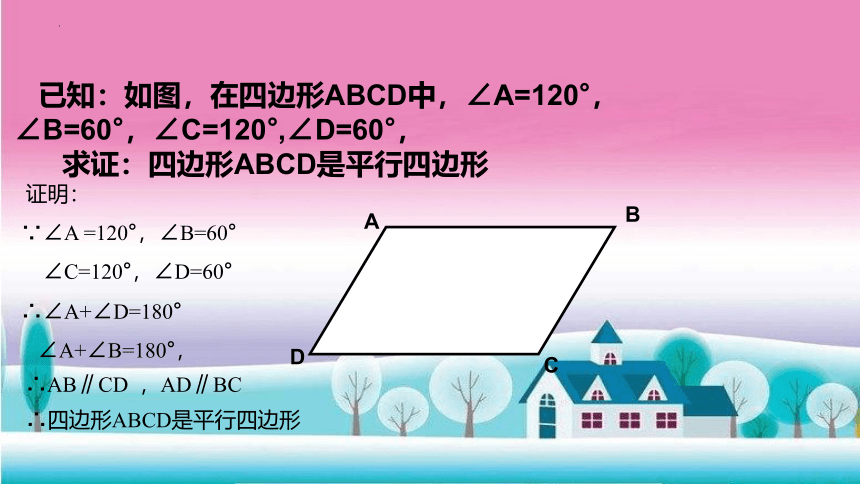
已知:如图,在四边形ABCD中,∠A=120°,
∠B=60°,∠C=120°,∠D=60°,
求证:四边形ABCD是平行四边形
C
B
D
A
∴∠A+∠D=180°
∠A+∠B=180°,
证明:
∴AB∥CD ,AD∥BC
∵∠A =120°,∠B=60°
∠C=120°,∠D=60°
∴四边形ABCD是平行四边形
与平行四边形判定有关的证明题
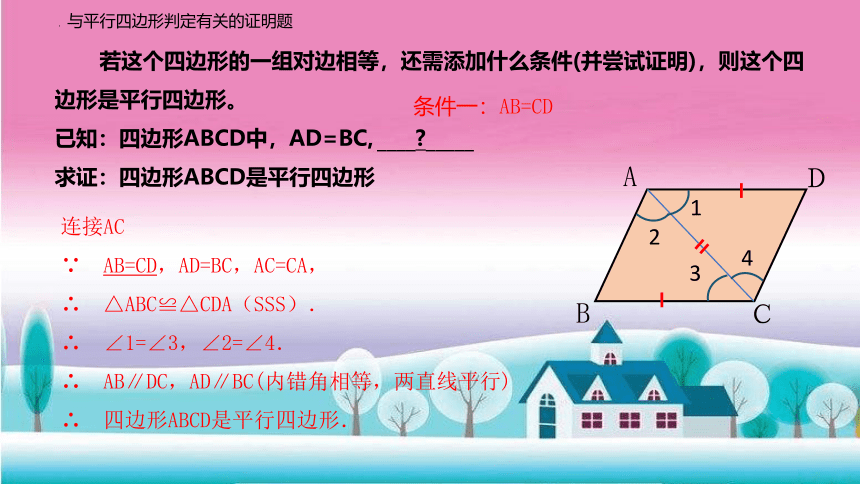
若这个四边形的一组对边相等,还需添加什么条件(并尝试证明),则这个四边形是平行四边形。
已知:四边形ABCD中,AD=BC, ____ _____
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
连接AC
∵ AB=CD,AD=BC,AC=CA,
∴ △ABC≌△CDA(SSS).
∴ ∠1=∠3,∠2=∠4.
∴ AB∥DC,AD∥BC(内错角相等,两直线平行)
∴ 四边形ABCD是平行四边形.
条件一:AB=CD
平行四边形的判定:
A
B
D
C
∵∠A=∠C ,∠B=∠D
∴四边形ABCD是平行四边形
两组对角分别相等的四边形是平行四边形.
你知道为什么了吗?
问题:为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了.你能说出其中的数学道理吗?
一组对边平行且相等的四边形是平行四边形
平行四边形的判定条件
文字语言 图形语言 几何语言
定义法 两组对边分别平行的四边形是平行四边形 ∵AB//CD, AD//BC,
∴四边形ABCD是平行四边形
判定方法1 两组对边分别相等的四边形是平行四边形 ∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形
判定方法2 两组对角分别相等的四边形是平行四边形 ∵∠A= ∠C, ∠B= ∠D,
∴四边形ABCD是平行四边形
判定方法3 对角线互相平分的四边形是平行四边形 ∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
判断题:
1.相邻的两个角都互补的四边形是平行四边形. ( )
√
火眼金睛
2.一组对边平行另一组对边相等的四边形是平行四边形 .( )
×
3.对角线相等的四边形是平行四边形. ( )
×
4.有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形
(×)
B
C
A
D
B
C
A
D
如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF,DE=BF,
求证:四边形DEBF是平行四边形.
判定平行四边形的条件
四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:
①AD∥BC;②AD=BC;③OA=OC;④OB=OD
从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
【详解】
①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
①③可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
①④可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形.
故选B.
如图,AB =DC=EF, AD=BC,DE=CF, 则图
中有哪些互相平行的线段?
AB ∥ DC∥ EF
AD ∥ BC
DE ∥ CF
A
B
C
D
E
F
一个三角形有几条中位线?你能在△ABC中画出它所有的中位线吗?
A
B
C
D
E
F
有三条,如图,△ABC的中位线是DE、DF、EF.
如图,在 ABCD中,已知两条对角线相交于
点O, E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。
画一画
A
D
C
B
E
F
G
H
O
证明:
D
E
延长DE到F,使EF=DE.
连接AF、CF、DC .
∵AE=EC,DE=EF ,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形,
∴CF AD ,
∴CF BD ,
又∵ ,
∴DF BC .
∴ DE∥BC, .
如图,在△ABC中,点D,E分别是AB,AC边的中点,
求证:
证一证
从边来判定:
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角来判定:
两组对角分别相等的四边形是平行四边形
从对角线来判定:
两条对角线互相平分的四边形是平行四边形
归纳:
平行四边形的判定方法
同学们,再见
18.1.2 平行四边形的判定
探索与思考
A
B
D
C
平行四边形的性质:
平行四边形对边相等
平行四边形对角线互相平分
根据逆命题内容,尝试依次画出四边形,它们是平行四边形吗?
平行四边形对角相等
平行四边形性质的逆命题:
两组对边分别相等的四边形是平行四边形。
两组对角分别相等的四边形是平行四边形。
对角线互相平分的四边形是平行四边形。
从教格言
让学生在轻松、快乐的氛围中成就梦想!
工人师傅在施工过程中不小心打破了一块平行四边形玻璃,刚好有两边是完好的,请同学们帮帮忙,有没有办法还原平行四边形?
A
B
C
小问题大学问
导 入 新 课
猜想:
两组对边分别相等的四边形是平行四边形.
探索平行四边形的判定条件
判定三 对角线互相平分的四边形是平行四边形。
已知:四边形ABCD中,AO=OC,BO=DO
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
O
∵AO=OC,BO=DO ,∠AOD = ∠COB ,
∴△AOD≌△COB(SAS).
∴∠1=∠3 ∴AD∥BC
同理 △AOB≌△COD(SAS).
∴ ∠2=∠4 ∴AB∥DC
∴四边形ABCD是平行四边形.
已知:如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
证明:如图,连接AC,
∵AB∥CD,
∴∠1=∠ .
又AB=CD,AC=CA,
∴△ABC≌ ( )
∴BC= ( )
∴四边形ABCD是平行四边形.( )
A
D
B
C
1
2
△CDA
SAS
AD
全等三角形的对应边相等
你还有其它证法吗?
A
D
B
C
1
2
o
探究新知
两组对边分别相等的四边形是平行四边形
2
已知:如图,在四边形ABCD中,∠A=120°,
∠B=60°,∠C=120°,∠D=60°,
求证:四边形ABCD是平行四边形
C
B
D
A
∴∠A+∠D=180°
∠A+∠B=180°,
证明:
∴AB∥CD ,AD∥BC
∵∠A =120°,∠B=60°
∠C=120°,∠D=60°
∴四边形ABCD是平行四边形
与平行四边形判定有关的证明题
若这个四边形的一组对边相等,还需添加什么条件(并尝试证明),则这个四边形是平行四边形。
已知:四边形ABCD中,AD=BC, ____ _____
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
连接AC
∵ AB=CD,AD=BC,AC=CA,
∴ △ABC≌△CDA(SSS).
∴ ∠1=∠3,∠2=∠4.
∴ AB∥DC,AD∥BC(内错角相等,两直线平行)
∴ 四边形ABCD是平行四边形.
条件一:AB=CD
平行四边形的判定:
A
B
D
C
∵∠A=∠C ,∠B=∠D
∴四边形ABCD是平行四边形
两组对角分别相等的四边形是平行四边形.
你知道为什么了吗?
问题:为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了.你能说出其中的数学道理吗?
一组对边平行且相等的四边形是平行四边形
平行四边形的判定条件
文字语言 图形语言 几何语言
定义法 两组对边分别平行的四边形是平行四边形 ∵AB//CD, AD//BC,
∴四边形ABCD是平行四边形
判定方法1 两组对边分别相等的四边形是平行四边形 ∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形
判定方法2 两组对角分别相等的四边形是平行四边形 ∵∠A= ∠C, ∠B= ∠D,
∴四边形ABCD是平行四边形
判定方法3 对角线互相平分的四边形是平行四边形 ∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
判断题:
1.相邻的两个角都互补的四边形是平行四边形. ( )
√
火眼金睛
2.一组对边平行另一组对边相等的四边形是平行四边形 .( )
×
3.对角线相等的四边形是平行四边形. ( )
×
4.有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形
(×)
B
C
A
D
B
C
A
D
如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF,DE=BF,
求证:四边形DEBF是平行四边形.
判定平行四边形的条件
四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:
①AD∥BC;②AD=BC;③OA=OC;④OB=OD
从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
【详解】
①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
①③可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
①④可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形.
故选B.
如图,AB =DC=EF, AD=BC,DE=CF, 则图
中有哪些互相平行的线段?
AB ∥ DC∥ EF
AD ∥ BC
DE ∥ CF
A
B
C
D
E
F
一个三角形有几条中位线?你能在△ABC中画出它所有的中位线吗?
A
B
C
D
E
F
有三条,如图,△ABC的中位线是DE、DF、EF.
如图,在 ABCD中,已知两条对角线相交于
点O, E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。
画一画
A
D
C
B
E
F
G
H
O
证明:
D
E
延长DE到F,使EF=DE.
连接AF、CF、DC .
∵AE=EC,DE=EF ,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形,
∴CF AD ,
∴CF BD ,
又∵ ,
∴DF BC .
∴ DE∥BC, .
如图,在△ABC中,点D,E分别是AB,AC边的中点,
求证:
证一证
从边来判定:
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角来判定:
两组对角分别相等的四边形是平行四边形
从对角线来判定:
两条对角线互相平分的四边形是平行四边形
归纳:
平行四边形的判定方法
同学们,再见
