19-2-2一次函数课件人教版八年级数学下册(共18张PPT)
文档属性
| 名称 | 19-2-2一次函数课件人教版八年级数学下册(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 849.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 17:15:34 | ||
图片预览






文档简介
(共18张PPT)
19.2.2 一次函数
学习目标
1.理解一次函数的概念,明确一次函数与正比例函数之间的联系。
2.会画一次函数的图象,掌握一次函数的性质。
3.能灵活运用一次函数的图象与性质解答有关问题。
下图是生活中弹簧称、电子称,同学们想过它们的原理吗?
引入
填空
函数图象上,则点的坐标是 .
正比例函数图象经过点
.
.某城市的市内电话的月收费额y(单位:元)包括:月租费22元,拨打电话x分钟的计时费按0.01元/分钟收取;
.把一个长10cm、宽5cm的长方形的长减少xcm,宽不变,长方形的面积y(单位:cm2)随x的值而变化.
y=-5x+50 (0≤ x ≤10)
y=0.01x+22
问题
表示函数的三种方法:
图像法
列表法
解析式法
…
气温 … -10 -13 …
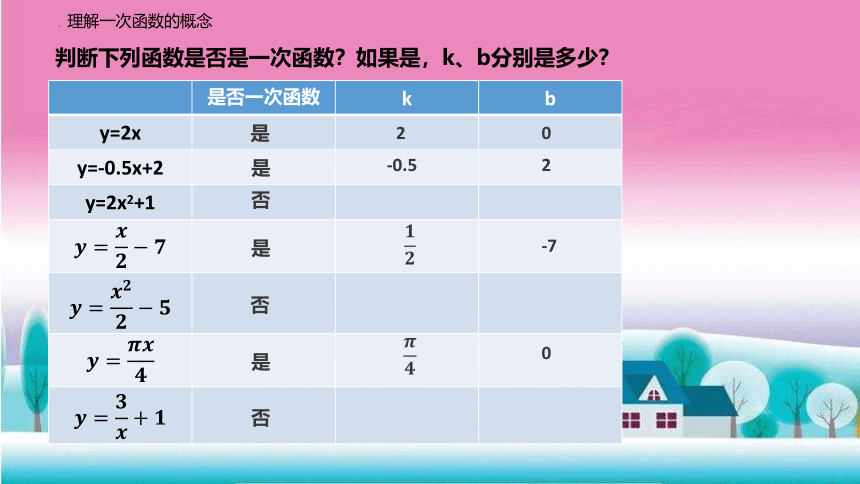
理解一次函数的概念
判断下列函数是否是一次函数?如果是,k、b分别是多少?
是否一次函数 k b
y=2x
y=-0.5x+2
y=2x2+1
是
是
是
是
2
0
-0.5
2
-7
0
否
否
否
问题
问题2 下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式,这些函数解析式有哪些共同特征?
某城市的市内电话的月收费额(单位:元)包括月租费22元和拨打电话的计时费(0.1元/ );
待定系数法
先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法。具体步骤如下图:
概念解析
一般地,形如(, 为常数, )的函数叫做一次函数.
思考 当时, 是什么函数?
( 为常数, )
正比例函数
观察与思考
画函数y=2x+1与y=2x-1的图象:
1.列表:
2.描点:
3.连线:
x 0 1
y=2x+1 1 3
y=2x-1 -1 1
x 0 1
y=-x+1 1 0
y=-x-1 -1 -2
y=-x+1(b>0)
y=-x-1 (b<0)
y=2x+1(b>0)
y=2x-1(b<0)
一次函数y=kx+b(b>0)与y轴的交点在原点上方;
一次函数y=kx+b(b<0)与y轴的交点在原点下方;
一次函数y=kx+b(k>0),y随x增大而增大;
一次函数y=kx+b(k<0),y随x增大而减小;
4.观察图像有何特点:
课堂练习
练习3 已知一次函数,
当3时,5,当4时,9,求的值.
解:由已知得:
解得:
一次函数的解析式为
理解一次函数的性质
在平面直角坐标系中,一次函数y=kx+b的图象如图所示,则k和b的取值范围是( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
【详解】∵一次函数y=kx+b的图象经过一、二、四象限,
∴k<0,b>0,
故选C.
理解一次函数的性质
当k<0时,一次函数y=kx-k的图象不经过( )
(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
解:因为一次函数,k<0,而b>0(-k>0),
所以图像经过一、二、四象限,
故不进过第三象限,
选C.
什么叫一次函数?
一般地,形如(, 为常数, )的函数叫做一次函数.
表示某个常数与自变量的积与常数的和。
它的右端是一个关于自变量的一次式,故为一次函数。
应用一次函数模型解决实际问题;
书写分段函数的解析式时要注意自变量的取值范围不重不漏.
对于一次函数,需要变量的几对对应值才能确定函数解析式?怎样求函数解析式?
课堂小结
知道函数的两组对应值,就可以确定的值,从而可以确定函数的解析式。
同学们,再见
19.2.2 一次函数
学习目标
1.理解一次函数的概念,明确一次函数与正比例函数之间的联系。
2.会画一次函数的图象,掌握一次函数的性质。
3.能灵活运用一次函数的图象与性质解答有关问题。
下图是生活中弹簧称、电子称,同学们想过它们的原理吗?
引入
填空
函数图象上,则点的坐标是 .
正比例函数图象经过点
.
.某城市的市内电话的月收费额y(单位:元)包括:月租费22元,拨打电话x分钟的计时费按0.01元/分钟收取;
.把一个长10cm、宽5cm的长方形的长减少xcm,宽不变,长方形的面积y(单位:cm2)随x的值而变化.
y=-5x+50 (0≤ x ≤10)
y=0.01x+22
问题
表示函数的三种方法:
图像法
列表法
解析式法
…
气温 … -10 -13 …
理解一次函数的概念
判断下列函数是否是一次函数?如果是,k、b分别是多少?
是否一次函数 k b
y=2x
y=-0.5x+2
y=2x2+1
是
是
是
是
2
0
-0.5
2
-7
0
否
否
否
问题
问题2 下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式,这些函数解析式有哪些共同特征?
某城市的市内电话的月收费额(单位:元)包括月租费22元和拨打电话的计时费(0.1元/ );
待定系数法
先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法。具体步骤如下图:
概念解析
一般地,形如(, 为常数, )的函数叫做一次函数.
思考 当时, 是什么函数?
( 为常数, )
正比例函数
观察与思考
画函数y=2x+1与y=2x-1的图象:
1.列表:
2.描点:
3.连线:
x 0 1
y=2x+1 1 3
y=2x-1 -1 1
x 0 1
y=-x+1 1 0
y=-x-1 -1 -2
y=-x+1(b>0)
y=-x-1 (b<0)
y=2x+1(b>0)
y=2x-1(b<0)
一次函数y=kx+b(b>0)与y轴的交点在原点上方;
一次函数y=kx+b(b<0)与y轴的交点在原点下方;
一次函数y=kx+b(k>0),y随x增大而增大;
一次函数y=kx+b(k<0),y随x增大而减小;
4.观察图像有何特点:
课堂练习
练习3 已知一次函数,
当3时,5,当4时,9,求的值.
解:由已知得:
解得:
一次函数的解析式为
理解一次函数的性质
在平面直角坐标系中,一次函数y=kx+b的图象如图所示,则k和b的取值范围是( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
【详解】∵一次函数y=kx+b的图象经过一、二、四象限,
∴k<0,b>0,
故选C.
理解一次函数的性质
当k<0时,一次函数y=kx-k的图象不经过( )
(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
解:因为一次函数,k<0,而b>0(-k>0),
所以图像经过一、二、四象限,
故不进过第三象限,
选C.
什么叫一次函数?
一般地,形如(, 为常数, )的函数叫做一次函数.
表示某个常数与自变量的积与常数的和。
它的右端是一个关于自变量的一次式,故为一次函数。
应用一次函数模型解决实际问题;
书写分段函数的解析式时要注意自变量的取值范围不重不漏.
对于一次函数,需要变量的几对对应值才能确定函数解析式?怎样求函数解析式?
课堂小结
知道函数的两组对应值,就可以确定的值,从而可以确定函数的解析式。
同学们,再见
