人教版数学八年级下册第十八章 平行四边形 复习课件(共18张PPT)
文档属性
| 名称 | 人教版数学八年级下册第十八章 平行四边形 复习课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 562.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 20:56:50 | ||
图片预览




文档简介
(共18张PPT)
18 复习与测试
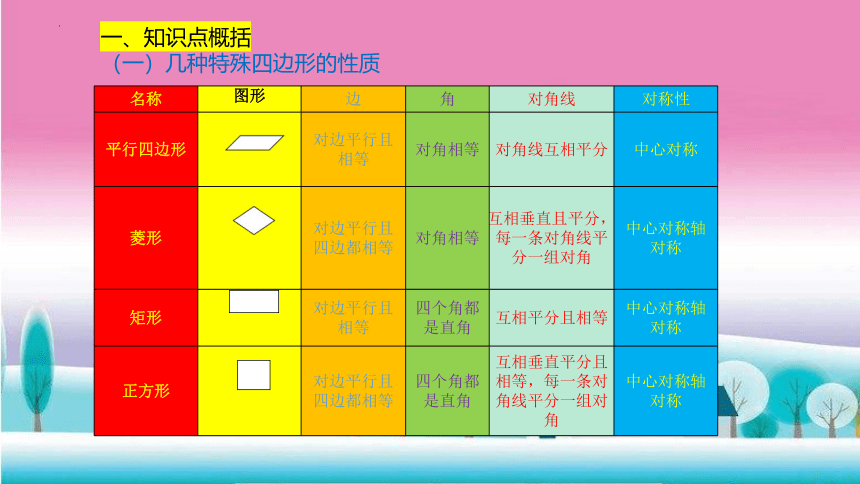
名称 图形 边 角 对角线 对称性
平行四边形 对边平行且相等 对角相等 对角线互相平分 中心对称
菱形 对边平行且四边都相等 对角相等 互相垂直且平分,每一条对角线平分一组对角 中心对称轴对称
矩形 对边平行且相等 四个角都是直角 互相平分且相等 中心对称轴对称
正方形 对边平行且四边都相等 四个角都是直角 互相垂直平分且相等,每一条对角线平分一组对角 中心对称轴对称
一、知识点概括
(一)几种特殊四边形的性质
1、 四边形ABCD是平行四边形,则下列叙述不正确的是( )
A、任意两个相邻角都互补 B、任意两个相邻边都相等
C、对边平行且相等 D、对角线互相平分
2、下列四边形不是矩形的是( )
A、有三个角都是直角的四边形 B、四个角都相等的四边形
C、一组对边平行,且对角相等的四边形
D、对角线相等且互相平分的四边形
3、能判定一个四边形是菱形的是( )
A、对角线互相平分且相等 B、对角线互相垂直且平分
C、对角线互相垂直且一组对角相等
D、对角线互相垂直且一条对角线平分一组对角
4、正方形具有而菱形不一定具有的性质是( )
A、四条边都相等 B、对角线相等
C、对角线垂直且互相平分 D、对角线平分一组对角
5、下列图形中,是中心对称图形,但不是轴对称图形的是( )
A、正方形 B、矩形 C、菱形 D、平行四边形
一.基础训练
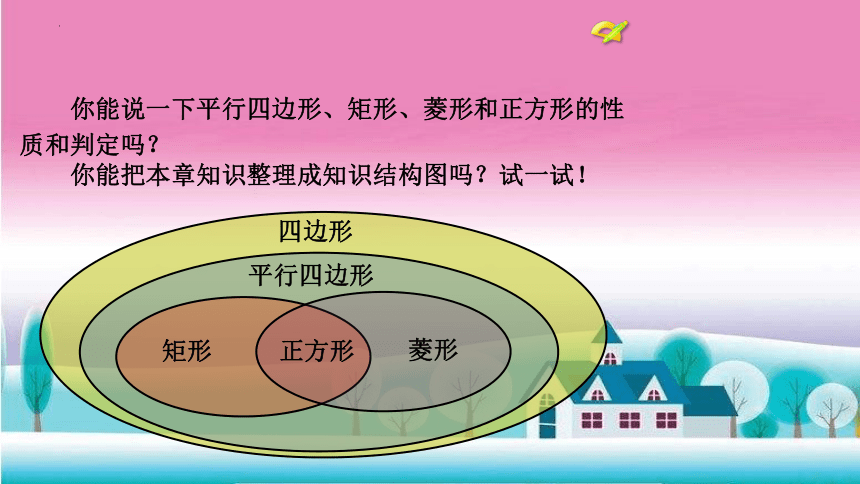
你能说一下平行四边形、矩形、菱形和正方形的性
质和判定吗?
你能把本章知识整理成知识结构图吗?试一试!
矩形
菱形
正方形
平行四边形
四边形
四边形 条件
①定义:两组对边分别平行 ②两组对边分别相等
③一组对边平行且相等 ④对角线互相平分
①定义:有一外角是直角的平行四边形
②三个角是直角的四边形
③对角线相等的平行四边形
①定义:一组邻边相等的平行四边形
②四条边都相等的四边形
③对角线互相垂直的平行四边形
①定义:一组邻边相等且有一个角是直角的平行四边形
②有一组邻边相等的矩形 ③有一个角是直角的菱形
几种特殊四边形的常用判定方法
二
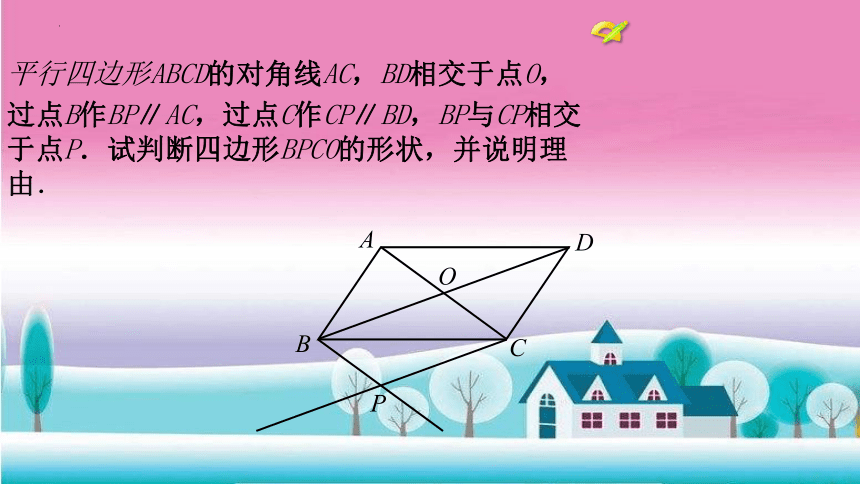
平行四边形ABCD的对角线AC,BD相交于点O,
过点B作BP∥AC,过点C作CP∥BD,BP与CP相交于点P.试判断四边形BPCO的形状,并说明理由.
A
B
C
D
O
P
考点一 平行四边形的性质与判定
考点讲练
例1 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.
(1)求证:四边形DEGF是平行四边形;
(2)如果点G是BC的中点,且BC=12,DC=10,求
四边形AGCD的面积.
解:(1)∵AG∥DC,AD∥BC,
∴四边形AGCD是平行四边形,
∴AG=DC.
如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是__________位置关系是_____
AF=BE
AF⊥BE
(图1)
理由:∵四边形ABCD是正方形
∴AB=DA=DC,∠BAD=∠ADC=90
又∵△ADE和△DCF是等边三角形
∴AE=DA,DF=DC,
∠DAE=60 ,∠CDF=60
∴AE=DF
∠BAD+∠DAE=∠ADC+∠CDF
∴∠BAE=∠ADF
∴△ABE≌△DAF(SAS)
∴ BE=AF,∠ABE=∠DAF
∵∠BAF+∠DAF=∠BAD=90
∴∠BAF+∠ABE=90
O
∴∠AOB=180 -(∠BAF+∠ABE)
=90
∴AF⊥BE
变式 若将 ABCD改为矩形ABCD,过点B作BP∥AC,过点C作CP∥BD,BP与CP相交于点P. BPCO是什么四边形?AOPB呢
A
B
C
D
O
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,求DF的值.
解:(2)图②中:AC+DE=DF.
图③中:AC+DF=DE.
(3)当如图①的情况,DF=AC-DE=6-4=2;
当如图②的情况,DF=AC+DE=6+4=10.
如图,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD,EC与BD相交于点G,与AD相交于点F,AF=AB
(1)求证:BD⊥EC;
(2)如图2,连接AG,求证:
(1)证明:∵四边形 是矩形,
点E在BA的延长线上,
∴
∴
两张等宽的纸条交叉重叠在一起,猜想重叠部分的四边形ABCD是菱形,能否为特殊的菱形?
F
E
例 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=
BC.若AB=12,求EF的长.
解:连接CD,
∵点D,E分别是边AB,AC的中点,
∴DE∥BC,DE= BC,DC= AB.
∵CF= BC,
∴DE ∥FC,DE =FC,
∴四边形DEFC是平行四边形,
∴DC=EF,
∴EF= AB=6.
.如图,∠MON=90°,正方形 ABCD的顶点A、B分别在OM、
ON上,AB=13,OB=5,E为
AC上一点,且∠EBC=∠CBN,
直线DE与ON交于点F.
(1)求证BE=DE;
(2)判断DF与ON的位置关系,
并说明理由;
(3)△BEF的周长为
(3)解:过D点作DG垂直于OM,交点为G,
∵四边形ABCD是正方形,
∴AD=AB,∠BAD=90°,
∴∠DAG+∠BAO=90°,
∵∠ABO+∠BAO=90°,
∴∠DAG=∠ABO,
又∵∠MON=90°,DG⊥OM,
∴△ADG≌△BAO,
∴DG=AO,GA=OB=5,
∵AB=13,OB=5,
根据勾股定理可得AO=12,
由(2)可知DF⊥ON,
又∵∠MON=90°,DG⊥OM,
∴四边形OFDG是矩形,
∴OF=DG=AO=12,DF=OG=17,
由(1)可知BE=DE,
∴△BEF的周长=DF+BF=17+(12-5)=24.
把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是?
例 如图,已知在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE;
(1)试判断四边形BECF是什么四边形?并说明理由;
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
解:(1)四边形BECF是菱形.
理由如下:∵EF垂直平分BC,
∴BF=FC,BE=EC,
∴∠3=∠1.
∵∠ACB=90°,
∴∠3+∠4=90°,∠1+∠2=90°,∴∠2=∠4,
∴EC=AE,∴BE=AE.
∵CF=AE,
∴BE=EC=CF=BF,
∴四边形BECF是菱形.
(2)当∠A=45°时,菱形BECF是正方形.
证明如下:∵∠A=45°,∠ACB=90°,
∴∠CBA=45°,∴∠EBF=2∠CBA=90°,
∴菱形BECF是正方形.
方法总结
正方形的判定方法:①先判定四边形是矩形,再判定这个矩形有一组邻边相等;②先判定四边形是菱形,再判定这个矩形有一个角为直角;③还可以先判定四边形是平行四边形,再用①或②进行判定.
同学们,再见
18 复习与测试
名称 图形 边 角 对角线 对称性
平行四边形 对边平行且相等 对角相等 对角线互相平分 中心对称
菱形 对边平行且四边都相等 对角相等 互相垂直且平分,每一条对角线平分一组对角 中心对称轴对称
矩形 对边平行且相等 四个角都是直角 互相平分且相等 中心对称轴对称
正方形 对边平行且四边都相等 四个角都是直角 互相垂直平分且相等,每一条对角线平分一组对角 中心对称轴对称
一、知识点概括
(一)几种特殊四边形的性质
1、 四边形ABCD是平行四边形,则下列叙述不正确的是( )
A、任意两个相邻角都互补 B、任意两个相邻边都相等
C、对边平行且相等 D、对角线互相平分
2、下列四边形不是矩形的是( )
A、有三个角都是直角的四边形 B、四个角都相等的四边形
C、一组对边平行,且对角相等的四边形
D、对角线相等且互相平分的四边形
3、能判定一个四边形是菱形的是( )
A、对角线互相平分且相等 B、对角线互相垂直且平分
C、对角线互相垂直且一组对角相等
D、对角线互相垂直且一条对角线平分一组对角
4、正方形具有而菱形不一定具有的性质是( )
A、四条边都相等 B、对角线相等
C、对角线垂直且互相平分 D、对角线平分一组对角
5、下列图形中,是中心对称图形,但不是轴对称图形的是( )
A、正方形 B、矩形 C、菱形 D、平行四边形
一.基础训练
你能说一下平行四边形、矩形、菱形和正方形的性
质和判定吗?
你能把本章知识整理成知识结构图吗?试一试!
矩形
菱形
正方形
平行四边形
四边形
四边形 条件
①定义:两组对边分别平行 ②两组对边分别相等
③一组对边平行且相等 ④对角线互相平分
①定义:有一外角是直角的平行四边形
②三个角是直角的四边形
③对角线相等的平行四边形
①定义:一组邻边相等的平行四边形
②四条边都相等的四边形
③对角线互相垂直的平行四边形
①定义:一组邻边相等且有一个角是直角的平行四边形
②有一组邻边相等的矩形 ③有一个角是直角的菱形
几种特殊四边形的常用判定方法
二
平行四边形ABCD的对角线AC,BD相交于点O,
过点B作BP∥AC,过点C作CP∥BD,BP与CP相交于点P.试判断四边形BPCO的形状,并说明理由.
A
B
C
D
O
P
考点一 平行四边形的性质与判定
考点讲练
例1 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.
(1)求证:四边形DEGF是平行四边形;
(2)如果点G是BC的中点,且BC=12,DC=10,求
四边形AGCD的面积.
解:(1)∵AG∥DC,AD∥BC,
∴四边形AGCD是平行四边形,
∴AG=DC.
如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是__________位置关系是_____
AF=BE
AF⊥BE
(图1)
理由:∵四边形ABCD是正方形
∴AB=DA=DC,∠BAD=∠ADC=90
又∵△ADE和△DCF是等边三角形
∴AE=DA,DF=DC,
∠DAE=60 ,∠CDF=60
∴AE=DF
∠BAD+∠DAE=∠ADC+∠CDF
∴∠BAE=∠ADF
∴△ABE≌△DAF(SAS)
∴ BE=AF,∠ABE=∠DAF
∵∠BAF+∠DAF=∠BAD=90
∴∠BAF+∠ABE=90
O
∴∠AOB=180 -(∠BAF+∠ABE)
=90
∴AF⊥BE
变式 若将 ABCD改为矩形ABCD,过点B作BP∥AC,过点C作CP∥BD,BP与CP相交于点P. BPCO是什么四边形?AOPB呢
A
B
C
D
O
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,求DF的值.
解:(2)图②中:AC+DE=DF.
图③中:AC+DF=DE.
(3)当如图①的情况,DF=AC-DE=6-4=2;
当如图②的情况,DF=AC+DE=6+4=10.
如图,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD,EC与BD相交于点G,与AD相交于点F,AF=AB
(1)求证:BD⊥EC;
(2)如图2,连接AG,求证:
(1)证明:∵四边形 是矩形,
点E在BA的延长线上,
∴
∴
两张等宽的纸条交叉重叠在一起,猜想重叠部分的四边形ABCD是菱形,能否为特殊的菱形?
F
E
例 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=
BC.若AB=12,求EF的长.
解:连接CD,
∵点D,E分别是边AB,AC的中点,
∴DE∥BC,DE= BC,DC= AB.
∵CF= BC,
∴DE ∥FC,DE =FC,
∴四边形DEFC是平行四边形,
∴DC=EF,
∴EF= AB=6.
.如图,∠MON=90°,正方形 ABCD的顶点A、B分别在OM、
ON上,AB=13,OB=5,E为
AC上一点,且∠EBC=∠CBN,
直线DE与ON交于点F.
(1)求证BE=DE;
(2)判断DF与ON的位置关系,
并说明理由;
(3)△BEF的周长为
(3)解:过D点作DG垂直于OM,交点为G,
∵四边形ABCD是正方形,
∴AD=AB,∠BAD=90°,
∴∠DAG+∠BAO=90°,
∵∠ABO+∠BAO=90°,
∴∠DAG=∠ABO,
又∵∠MON=90°,DG⊥OM,
∴△ADG≌△BAO,
∴DG=AO,GA=OB=5,
∵AB=13,OB=5,
根据勾股定理可得AO=12,
由(2)可知DF⊥ON,
又∵∠MON=90°,DG⊥OM,
∴四边形OFDG是矩形,
∴OF=DG=AO=12,DF=OG=17,
由(1)可知BE=DE,
∴△BEF的周长=DF+BF=17+(12-5)=24.
把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是?
例 如图,已知在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE;
(1)试判断四边形BECF是什么四边形?并说明理由;
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
解:(1)四边形BECF是菱形.
理由如下:∵EF垂直平分BC,
∴BF=FC,BE=EC,
∴∠3=∠1.
∵∠ACB=90°,
∴∠3+∠4=90°,∠1+∠2=90°,∴∠2=∠4,
∴EC=AE,∴BE=AE.
∵CF=AE,
∴BE=EC=CF=BF,
∴四边形BECF是菱形.
(2)当∠A=45°时,菱形BECF是正方形.
证明如下:∵∠A=45°,∠ACB=90°,
∴∠CBA=45°,∴∠EBF=2∠CBA=90°,
∴菱形BECF是正方形.
方法总结
正方形的判定方法:①先判定四边形是矩形,再判定这个矩形有一组邻边相等;②先判定四边形是菱形,再判定这个矩形有一个角为直角;③还可以先判定四边形是平行四边形,再用①或②进行判定.
同学们,再见
