人教版数学七年级下册第五章相交线与平行线 复习课件(共19张PPT)
文档属性
| 名称 | 人教版数学七年级下册第五章相交线与平行线 复习课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 411.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 20:58:09 | ||
图片预览




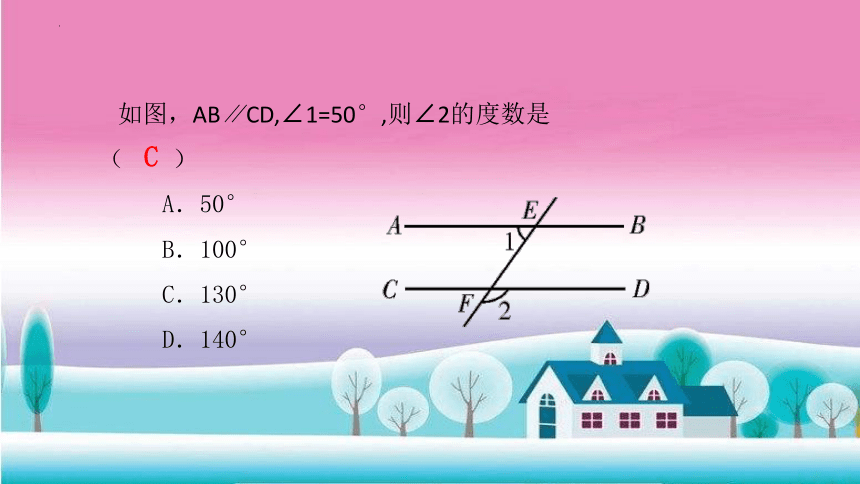
文档简介
(共19张PPT)
5 复习与测试
1.进一步熟悉平行线的判定方法和性质;
2.能综合运用平行线的性质和判定进行推理和计算;(重点、难点)
一、学习目标
1、 根据定义
2、平行于同一条直线的两条直线互相平行
3、 在同一平面内,垂直于同一条直线的两条直线平行
4、同位角相等,两直线平行
5、内错角相等,两直线平行
6、同旁内角互补,两直线平行
(形)直线平行
>
角的关系(数)
1、两直线平行,同位角相等
2、两直线平行,内错角相等
3、两直线平行,同旁内角互补
平行线的判定方法
平行线的性质
直线平行(形)
(数)角的关系
>
判定
性质
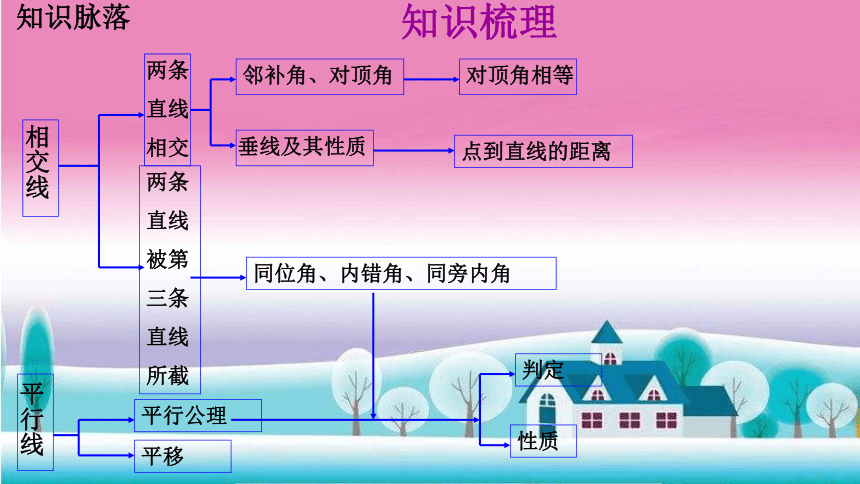
知识脉落
相交线
两条
直线
相交
邻补角、对顶角
对顶角相等
垂线及其性质
点到直线的距离
两条
直线
被第
三条
直线
所截
同位角、内错角、同旁内角
平行线
平行公理
平移
判定
性质
知识梳理
例2 如图,直线AB、CD,EF相交于点O,∠1=40°,∠BOC=110°,求∠2的度数.
解:因为∠1=40°,
∠BOC=110°(已知),
所以∠BOF=∠BOC-∠1
=110°-40°=70°.
因为∠BOF=∠2(对顶角相等),
所以∠2=70°(等量代换).
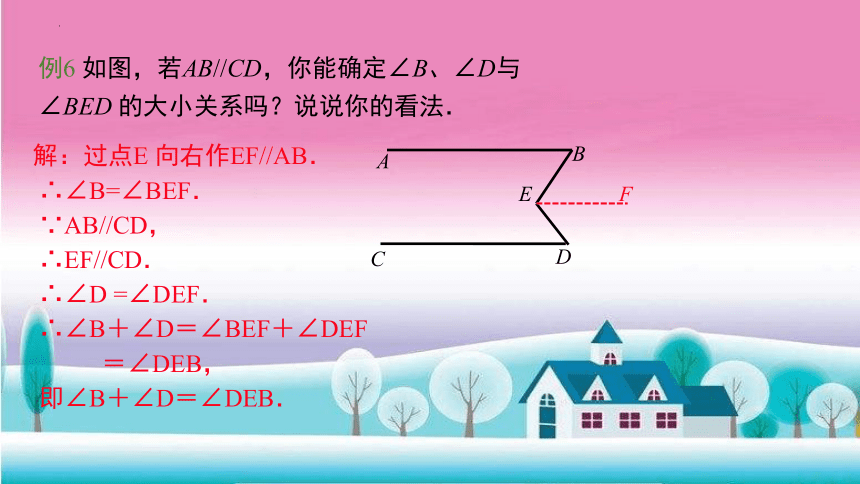
例6 如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法.
B
D
C
E
A
解:过点E 向右作EF//AB.
∴∠B=∠BEF.
∵AB//CD,
∴EF//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF
=∠DEB,
即∠B+∠D=∠DEB.
F
如图,AB∥CD,∠1=50°,则∠2的度数是 ( )
A.50°
B.100°
C.130°
D.140°
C
平移的性质:
1、平移后的图形改变的是图形的 ,不改变图形的______和______.
2、图形平移的方向,________(填一定或不一定)是水平的.
3、新图形的每一点,都是由_____图形的某一点移动后得到的,这两个点叫做_______,连接各组对应点的线段______________.
4、经过平移所得的图形与原来的图形的对应线段 ,对应角 ,对应点所连的线段_____________.
位置
形状
大小
原
不一定
对应点
平行(或在同一天直线上)且相等
相等
相等
平行且相等
知识梳理
1.如图,直线AB、CD、EF相交,若∠1 +∠5=180°,
找出图中与∠1 相等的角.
D
B
E
O
A
C
F
解:∵ ∠1= ∠3(对顶角相等),
1
2
3
4
5
6
8
7
∠5+∠8=180 °,且∠1 +∠5=180°,
∴∠8= ∠1.
∵ ∠8= ∠6(对顶角相等),
∴∠6= ∠1.
如图,AB∥CD,∠A=∠C, 试判断AD与BC的位置关系 为什么
解: AD∥BC,理由如下:
∵∠A=∠C
∵ AB∥CD
∴ ∠A+∠D=180°( )
两直线平行,同旁内角互补
∴ ∠A+∠D=180°( )
∴ AD∥BC( )
等量代换
同旁内角互补,两直线平行
解法一:
A
B
C
D
O
(二)、垂直:
2、画法:
3、性质:
两条直线相交所形成的四个角中有一个是直角时叫两条直线互相垂直。
过一点画一条直线的垂线。
P
a
Q
(1)、过一点有且只有一条直线垂直于已知直线。
p
A
B
C
D
E
(2)、 垂线段最短。
点到直线的距离:
b
b
c
1、定义:
知识梳理
下列命题是真命题的有( )
A、相等的角是对顶角
B、不是对顶角的角不相等
C、对顶角必相等
D、有公共顶点的角是对顶角
E 、邻补角的和一定是180度
F、互补的两个角一定是邻补角
G、两条直线相交,只要其中一个角的大小确定了,那么另外三个角的大小就确定了
C、E、G
知识运用
填空:如图,
(1)∠1= 时,AB∥CD;
(2)AD∥BC时,∠3= .
D
1
2
3
4
5
A
B
C
F
E
∠2
∠5
或∠4
如图,AD⊥BC,垂足为D,点E在线段AB上,∠C+∠ADE=90°. 求证:DE∥AC;
证明:∵AD⊥BC,
∴∠C+∠CAD=90°.
∵∠C+∠ADE=90°,
∴∠CAD=∠ADE.
∴DE∥AC.
(垂直的定义)
(等量代换)
(内错角相等,两直线平行)
若两条平行线被第三条直线所截,则一组内错角的平分线互相( )
A 垂直 B 平行 C 重合 D 相交
两条平行线被第三条直线所截,下列说法错误是:( )
A.同旁内角的平分线互相垂直
B.内错角的平分线互相平行
C.同旁内角的平分线互相平行
D.同位角的平分线互相平行.
C
B
如图,已知∠AEM=∠DGN,则你能说明AB平行于CD吗?
变式:若∠AEM=∠DGN,EF、GH分别平分∠AEG和∠CGN,则图中还有平行线吗?
EF∥GH
如果要构造第三条直线与AB或CD平行,在什么地方作呢?
A
B
D
C
E
解: 如图,过点E作EF∥AB
1
2
F
∴ ∠B+∠1=180°
( )
∵ ∠B+∠BED +∠D=360°
即∠B+∠1 +∠2+∠D=360°
∴ ∠2+∠D=180°
∴ EF∥CD( )
∵ EF∥AB
∴ AB∥CD( )
两直线平行,同旁内角互补
同旁内角互补,两直线平行
平行于同一直线的两直线平行
解法一:
总结评价
目标再现
18
1 掌握本章的知识脉落.
2 巩固本章基础知识,掌握本章的
基本技能,灵活运用本章的知识解
决实际问题.
同学们,再见
5 复习与测试
1.进一步熟悉平行线的判定方法和性质;
2.能综合运用平行线的性质和判定进行推理和计算;(重点、难点)
一、学习目标
1、 根据定义
2、平行于同一条直线的两条直线互相平行
3、 在同一平面内,垂直于同一条直线的两条直线平行
4、同位角相等,两直线平行
5、内错角相等,两直线平行
6、同旁内角互补,两直线平行
(形)直线平行
>
角的关系(数)
1、两直线平行,同位角相等
2、两直线平行,内错角相等
3、两直线平行,同旁内角互补
平行线的判定方法
平行线的性质
直线平行(形)
(数)角的关系
>
判定
性质
知识脉落
相交线
两条
直线
相交
邻补角、对顶角
对顶角相等
垂线及其性质
点到直线的距离
两条
直线
被第
三条
直线
所截
同位角、内错角、同旁内角
平行线
平行公理
平移
判定
性质
知识梳理
例2 如图,直线AB、CD,EF相交于点O,∠1=40°,∠BOC=110°,求∠2的度数.
解:因为∠1=40°,
∠BOC=110°(已知),
所以∠BOF=∠BOC-∠1
=110°-40°=70°.
因为∠BOF=∠2(对顶角相等),
所以∠2=70°(等量代换).
例6 如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法.
B
D
C
E
A
解:过点E 向右作EF//AB.
∴∠B=∠BEF.
∵AB//CD,
∴EF//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF
=∠DEB,
即∠B+∠D=∠DEB.
F
如图,AB∥CD,∠1=50°,则∠2的度数是 ( )
A.50°
B.100°
C.130°
D.140°
C
平移的性质:
1、平移后的图形改变的是图形的 ,不改变图形的______和______.
2、图形平移的方向,________(填一定或不一定)是水平的.
3、新图形的每一点,都是由_____图形的某一点移动后得到的,这两个点叫做_______,连接各组对应点的线段______________.
4、经过平移所得的图形与原来的图形的对应线段 ,对应角 ,对应点所连的线段_____________.
位置
形状
大小
原
不一定
对应点
平行(或在同一天直线上)且相等
相等
相等
平行且相等
知识梳理
1.如图,直线AB、CD、EF相交,若∠1 +∠5=180°,
找出图中与∠1 相等的角.
D
B
E
O
A
C
F
解:∵ ∠1= ∠3(对顶角相等),
1
2
3
4
5
6
8
7
∠5+∠8=180 °,且∠1 +∠5=180°,
∴∠8= ∠1.
∵ ∠8= ∠6(对顶角相等),
∴∠6= ∠1.
如图,AB∥CD,∠A=∠C, 试判断AD与BC的位置关系 为什么
解: AD∥BC,理由如下:
∵∠A=∠C
∵ AB∥CD
∴ ∠A+∠D=180°( )
两直线平行,同旁内角互补
∴ ∠A+∠D=180°( )
∴ AD∥BC( )
等量代换
同旁内角互补,两直线平行
解法一:
A
B
C
D
O
(二)、垂直:
2、画法:
3、性质:
两条直线相交所形成的四个角中有一个是直角时叫两条直线互相垂直。
过一点画一条直线的垂线。
P
a
Q
(1)、过一点有且只有一条直线垂直于已知直线。
p
A
B
C
D
E
(2)、 垂线段最短。
点到直线的距离:
b
b
c
1、定义:
知识梳理
下列命题是真命题的有( )
A、相等的角是对顶角
B、不是对顶角的角不相等
C、对顶角必相等
D、有公共顶点的角是对顶角
E 、邻补角的和一定是180度
F、互补的两个角一定是邻补角
G、两条直线相交,只要其中一个角的大小确定了,那么另外三个角的大小就确定了
C、E、G
知识运用
填空:如图,
(1)∠1= 时,AB∥CD;
(2)AD∥BC时,∠3= .
D
1
2
3
4
5
A
B
C
F
E
∠2
∠5
或∠4
如图,AD⊥BC,垂足为D,点E在线段AB上,∠C+∠ADE=90°. 求证:DE∥AC;
证明:∵AD⊥BC,
∴∠C+∠CAD=90°.
∵∠C+∠ADE=90°,
∴∠CAD=∠ADE.
∴DE∥AC.
(垂直的定义)
(等量代换)
(内错角相等,两直线平行)
若两条平行线被第三条直线所截,则一组内错角的平分线互相( )
A 垂直 B 平行 C 重合 D 相交
两条平行线被第三条直线所截,下列说法错误是:( )
A.同旁内角的平分线互相垂直
B.内错角的平分线互相平行
C.同旁内角的平分线互相平行
D.同位角的平分线互相平行.
C
B
如图,已知∠AEM=∠DGN,则你能说明AB平行于CD吗?
变式:若∠AEM=∠DGN,EF、GH分别平分∠AEG和∠CGN,则图中还有平行线吗?
EF∥GH
如果要构造第三条直线与AB或CD平行,在什么地方作呢?
A
B
D
C
E
解: 如图,过点E作EF∥AB
1
2
F
∴ ∠B+∠1=180°
( )
∵ ∠B+∠BED +∠D=360°
即∠B+∠1 +∠2+∠D=360°
∴ ∠2+∠D=180°
∴ EF∥CD( )
∵ EF∥AB
∴ AB∥CD( )
两直线平行,同旁内角互补
同旁内角互补,两直线平行
平行于同一直线的两直线平行
解法一:
总结评价
目标再现
18
1 掌握本章的知识脉落.
2 巩固本章基础知识,掌握本章的
基本技能,灵活运用本章的知识解
决实际问题.
同学们,再见
