用几何法求二面角课件
图片预览



文档简介
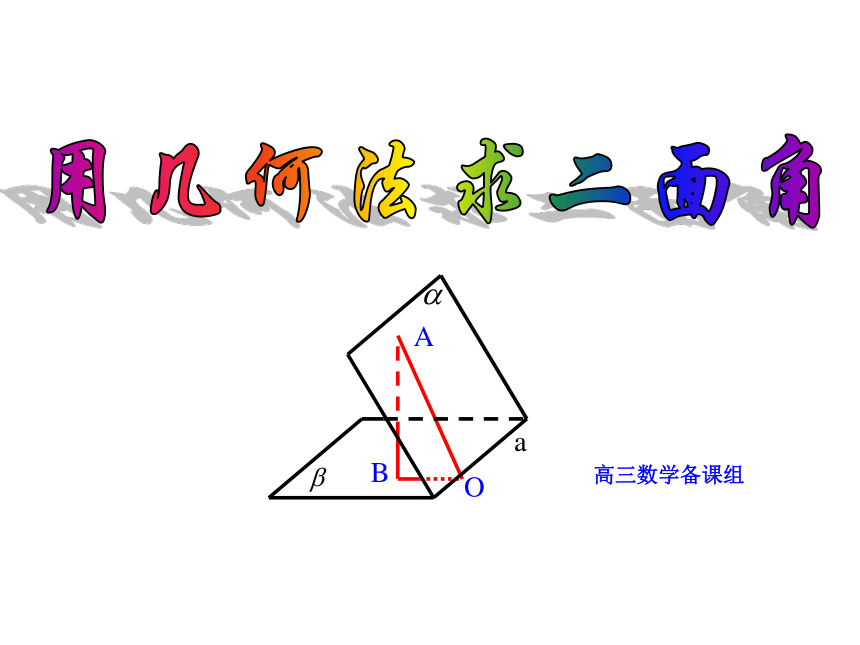
课件11张PPT。用几何法求二面角
高三数学备课组1、掌握二面角及二面角的平面角的概念。
2、掌握“找—证—求”二面角的平面角的基本方法,不断提高空间想象能力和运算求解能力。
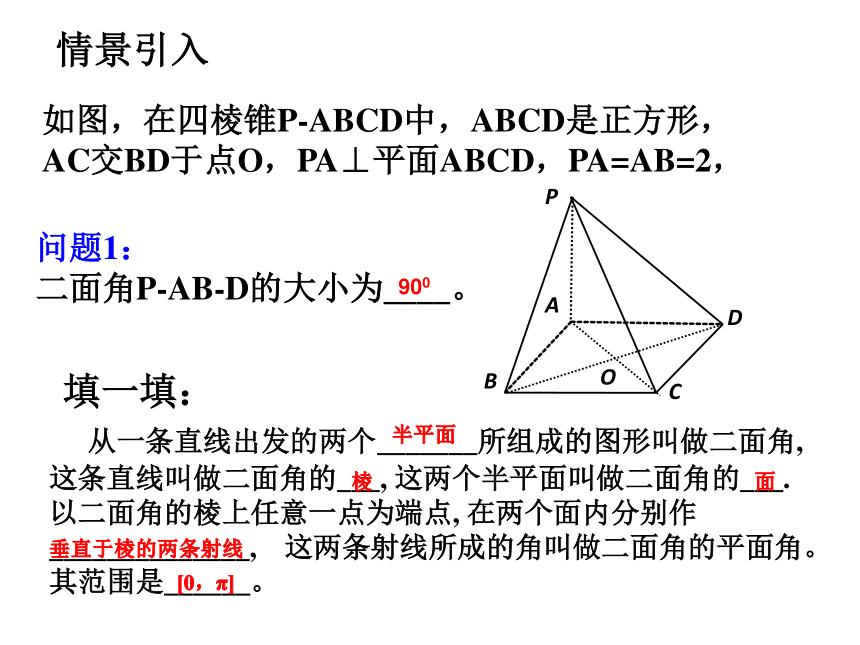
3、体会数学转化与化归的思想,增强把立体几何平面化处理的意识。学习目标:情景引入如图,在四棱锥P-ABCD中,ABCD是正方形,
AC交BD于点O,PA⊥平面ABCD,PA=AB=2,问题1:
二面角P-AB-D的大小为____。900 从一条直线出发的两个_______所组成的图形叫做二面角, 这条直线叫做二面角的___, 这两个半平面叫做二面角的___.
以二面角的棱上任意一点为端点, 在两个面内分别作
______________, 这两条射线所成的角叫做二面角的平面角。
其范围是______。填一填:半平面棱面垂直于棱的两条射线[0,π]质疑探究 1
用几何法求解二面角的步骤是什么?一找二证三求如图,在四棱锥P-ABCD中,ABCD是正方形,
AC交BD于点O,PA⊥平面ABCD,PA=AB=2,问题2:二面角P-CD-A的大小为_____。
问题3:请你在图中作出二面角P-BD-A的平面角,它的正切值为_______。
问题4:请你在图中作出二面角P-AC-B的平面角,它的大小为_____。450900H质疑探究 2
如何找二面角的平面角?关键是什么?质疑探究 2
如何找二面角的平面角?关键是什么?在一个平面内选一点A向
另一平面作垂线AB,垂足为B,
再过点B向棱a作垂线BO,
垂足为O,连结AO,
则∠AOB就是二面角的平面角。
可简记为“两垂一连”。 ABO关键是找或作出其中一个面的垂线如图,在四棱锥P-ABCD中,ABCD是正方形,
AC交BD于点O,PA⊥平面ABCD,PA=AB=2,问题5:求二面角B-PC-A的正弦值。E解:过B作BE⊥PC,连结OE,
由题4可知BO⊥面PAC,
而PC 面PAC,所以BO⊥PC,
又BE∩BO=B 所以PC⊥面BEO,
而EO 面BEO所以PC⊥EO,
所以∠BEO是二面角B-PC-A的平面角
在直角三角形PBC中,BO= ,
体验高考 O∠BEO是二面角B-PC-A的平面角,求解同上题小结:用几何法求解二面角的步骤?最关键的地方是什么?一找二证三求,
关键是找出二面角的平面角,
而找平面角的关键是找或作出其中一个面的垂线。作业
在四棱锥P-ABCD中,ABCD是平行四边形,
PA⊥平面ABCD,PA=AB=a,∠ABC=30°,
求二面角P-BC-A的正切值大小。
高三数学备课组1、掌握二面角及二面角的平面角的概念。
2、掌握“找—证—求”二面角的平面角的基本方法,不断提高空间想象能力和运算求解能力。
3、体会数学转化与化归的思想,增强把立体几何平面化处理的意识。学习目标:情景引入如图,在四棱锥P-ABCD中,ABCD是正方形,
AC交BD于点O,PA⊥平面ABCD,PA=AB=2,问题1:
二面角P-AB-D的大小为____。900 从一条直线出发的两个_______所组成的图形叫做二面角, 这条直线叫做二面角的___, 这两个半平面叫做二面角的___.
以二面角的棱上任意一点为端点, 在两个面内分别作
______________, 这两条射线所成的角叫做二面角的平面角。
其范围是______。填一填:半平面棱面垂直于棱的两条射线[0,π]质疑探究 1
用几何法求解二面角的步骤是什么?一找二证三求如图,在四棱锥P-ABCD中,ABCD是正方形,
AC交BD于点O,PA⊥平面ABCD,PA=AB=2,问题2:二面角P-CD-A的大小为_____。
问题3:请你在图中作出二面角P-BD-A的平面角,它的正切值为_______。
问题4:请你在图中作出二面角P-AC-B的平面角,它的大小为_____。450900H质疑探究 2
如何找二面角的平面角?关键是什么?质疑探究 2
如何找二面角的平面角?关键是什么?在一个平面内选一点A向
另一平面作垂线AB,垂足为B,
再过点B向棱a作垂线BO,
垂足为O,连结AO,
则∠AOB就是二面角的平面角。
可简记为“两垂一连”。 ABO关键是找或作出其中一个面的垂线如图,在四棱锥P-ABCD中,ABCD是正方形,
AC交BD于点O,PA⊥平面ABCD,PA=AB=2,问题5:求二面角B-PC-A的正弦值。E解:过B作BE⊥PC,连结OE,
由题4可知BO⊥面PAC,
而PC 面PAC,所以BO⊥PC,
又BE∩BO=B 所以PC⊥面BEO,
而EO 面BEO所以PC⊥EO,
所以∠BEO是二面角B-PC-A的平面角
在直角三角形PBC中,BO= ,
体验高考 O∠BEO是二面角B-PC-A的平面角,求解同上题小结:用几何法求解二面角的步骤?最关键的地方是什么?一找二证三求,
关键是找出二面角的平面角,
而找平面角的关键是找或作出其中一个面的垂线。作业
在四棱锥P-ABCD中,ABCD是平行四边形,
PA⊥平面ABCD,PA=AB=a,∠ABC=30°,
求二面角P-BC-A的正切值大小。
