用几何法求二面角教案(黄汉明)
文档属性
| 名称 | 用几何法求二面角教案(黄汉明) |

|
|
| 格式 | zip | ||
| 文件大小 | 114.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-14 00:00:00 | ||
图片预览

文档简介
用几何法求二面角教案(参考)
教学目标:
1.知识与技能:掌握二面角及二面角的平面角的概念并能用几何法求解。
2.过程与方法:通过实例教学提高逻辑思维能力,渗透等价转化思想;通过图形结构分析,掌握由定义出发“找—证—求”二面角的平面角的几何方法,提高空间想象能力和运算求解能力。
3.情感态度与价值观:培养学生探究数学的兴趣,增强把立体几何平面化处理的意识。
教学重点:用几何法求二面角。
教学难点:找二面角的平面角。
教学过程:
一.情景引入
教师:同学们好,这节课我们一起来探讨一下求二面角的几何法,至于向量法等我们复习到向量的应用再来研究。这两年高考都考到二面角,用传统的几何法解决都很方便,但是
得分率并不高,大家说说这是为什么?
学生全体:太难了,找不到这个角
教师:那我们就针对这个难点,
探究一下如何找二面角的平面角好吗?
学生全体:好。
教师:请看题。做好了举手回答。
如图,在四棱锥P-ABCD中,ABCD是正方形,
AC交BD于点O,PA⊥平面ABCD,PA=AB=2,
问题1:二面角P—AB—D的大小为__900__。
填一填
从一条直线出发的两个 半平面 所组成的图形叫做二面角,这条直线叫做二面角的 棱 ,这两个半平面叫做二面角的 面 。以二面角的棱上任意一点为端点,在两个面内分别作 垂直于棱的 两条射线,这两条射线所成的角叫做二面角的平面角,其范围是 [0,π] 。
质疑探究 1 用几何法求解二面角的步骤是什么?
学生A:一找二证三求。
二.题组变式训练
问题2:二面角P—CD—A的大小为___450___。
教师:请同学们找出平面角并说明理由
学生B:平面角是∠PDA,因为棱是CD,CD⊥DA,CD⊥DP,由定义可得
问题3:请你在上图中作出二面角P—BD—A的平面角,它的正切值为。
问题4:请你在上图中作出二面角P—AC—B的平面角,它的大小为 900 。
教师:请两个同学上来分别作图,并说明理由,解出值(也可以提问,教师作图)
学生C:连接PO,则∠POA是二面角的平面角,因为可以证明棱BD垂直面PAO,即BD垂直OA和OP,由定义可得。tan∠POA=PA/AO=
学生D:取PC中点H,连结HO,HB,则∠HOB是二面角的平面角,因为可以证明棱AC垂直OB和OH,由定义可得。
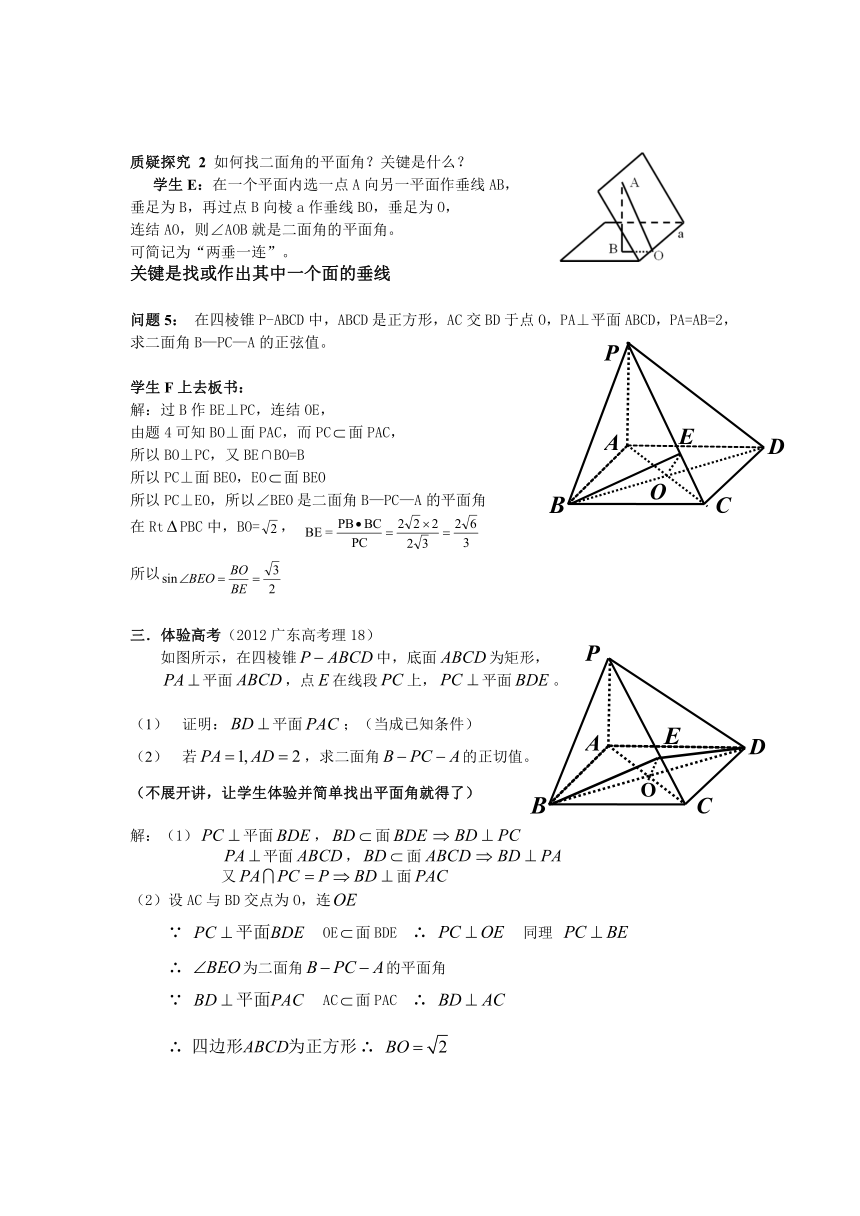
质疑探究 2 如何找二面角的平面角?关键是什么?
学生E:在一个平面内选一点A向另一平面作垂线AB,
垂足为B,再过点B向棱a作垂线BO,垂足为O,
连结AO,则∠AOB就是二面角的平面角。
可简记为“两垂一连”。
关键是找或作出其中一个面的垂线
问题5: 在四棱锥P-ABCD中,ABCD是正方形,AC交BD于点O,PA⊥平面ABCD,PA=AB=2,求二面角B—PC—A的正弦值。
学生F上去板书:
解:过B作BE⊥PC,连结OE,
由题4可知BO⊥面PAC,而PC面PAC,
所以BO⊥PC,又BE∩BO=B
所以PC⊥面BEO,EO面BEO
所以PC⊥EO,所以∠BEO是二面角B—PC—A的平面角
在RtPBC中,BO=,
所以
三.体验高考(2012广东高考理18)
如图所示,在四棱锥中,底面为矩形,
平面,点在线段上,平面。
证明:平面;(当成已知条件)
若,求二面角的正切值。
(不展开讲,让学生体验并简单找出平面角就得了)
解:(1)平面,面
平面,面
又面
(2)设AC与BD交点为O,连
∵ OE面BDE ∴ 同理
∴ 为二面角的平面角
∵ AC面PAC ∴
∴ ∴
在,
∴
∴ 二面角的平面角的正切值为3
四.小结:
用几何法求解二面角的步骤?最关键的地方是什么?
学生:一找二证三求,关键是找出二面角的平面角,而找平面角的关键是找或作出其中一个面的垂线。
五.作业:
在四棱锥P-ABCD中,ABCD是平行四边形,PA⊥平面ABCD,PA=AB=a,∠ABC=30°,求二面角P-BC-A的正切值大小。
解:(垂线法)如图PA⊥平面BD 过A作AH⊥BC于H,连结PH则PH⊥BC 又AH⊥BC
故∠PHA是二面角P-BC-A的平面角, 在Rt△ABH中,AH=ABsin∠ABC=aSin30°= 在Rt△PHA中,tan∠PHA=PA/AH=
六.板书设计:
七.教学后记:
八.课后练习
1.在四棱锥P-ABCD中,ABCD为正方形,PA⊥平面ABCD,PA=AB=a,求平面PBA与平面PDC所成二面角的大小为_________________
解(补形化为定义法)如图 将四棱锥P-ABCD补形得正方体ABCD-PQMN,
则PQ⊥PA、PD,于是∠APD是两面所成二面角的平面角。
在Rt△PAD中,PA=AD,则∠APD=45°。
即平面BAP与平面PDC所成二面角的大小为45°
2.(2011广东)在锥体P-ABCD中,ABCD是边长为1的菱形,且∠DAB=60,,PB=2, E,F分别是BC,PC的中点.
(1)证明:AD 平面DEF;
(2) 求二面角P-AD-B的余弦值。
(1)证明:取的中点,连接
∵,∴
∵在边长为1的菱形中,
∴△是等边三角形∴,
∴平面∴
∵分别是的中点∴∥,∥
∴,,∴平面
(2)解:由(1)知,
∴是二面角的平面角
易求得
∴
∴二面角的余弦值为
教学目标:
1.知识与技能:掌握二面角及二面角的平面角的概念并能用几何法求解。
2.过程与方法:通过实例教学提高逻辑思维能力,渗透等价转化思想;通过图形结构分析,掌握由定义出发“找—证—求”二面角的平面角的几何方法,提高空间想象能力和运算求解能力。
3.情感态度与价值观:培养学生探究数学的兴趣,增强把立体几何平面化处理的意识。
教学重点:用几何法求二面角。
教学难点:找二面角的平面角。
教学过程:
一.情景引入
教师:同学们好,这节课我们一起来探讨一下求二面角的几何法,至于向量法等我们复习到向量的应用再来研究。这两年高考都考到二面角,用传统的几何法解决都很方便,但是
得分率并不高,大家说说这是为什么?
学生全体:太难了,找不到这个角
教师:那我们就针对这个难点,
探究一下如何找二面角的平面角好吗?
学生全体:好。
教师:请看题。做好了举手回答。
如图,在四棱锥P-ABCD中,ABCD是正方形,
AC交BD于点O,PA⊥平面ABCD,PA=AB=2,
问题1:二面角P—AB—D的大小为__900__。
填一填
从一条直线出发的两个 半平面 所组成的图形叫做二面角,这条直线叫做二面角的 棱 ,这两个半平面叫做二面角的 面 。以二面角的棱上任意一点为端点,在两个面内分别作 垂直于棱的 两条射线,这两条射线所成的角叫做二面角的平面角,其范围是 [0,π] 。
质疑探究 1 用几何法求解二面角的步骤是什么?
学生A:一找二证三求。
二.题组变式训练
问题2:二面角P—CD—A的大小为___450___。
教师:请同学们找出平面角并说明理由
学生B:平面角是∠PDA,因为棱是CD,CD⊥DA,CD⊥DP,由定义可得
问题3:请你在上图中作出二面角P—BD—A的平面角,它的正切值为。
问题4:请你在上图中作出二面角P—AC—B的平面角,它的大小为 900 。
教师:请两个同学上来分别作图,并说明理由,解出值(也可以提问,教师作图)
学生C:连接PO,则∠POA是二面角的平面角,因为可以证明棱BD垂直面PAO,即BD垂直OA和OP,由定义可得。tan∠POA=PA/AO=
学生D:取PC中点H,连结HO,HB,则∠HOB是二面角的平面角,因为可以证明棱AC垂直OB和OH,由定义可得。
质疑探究 2 如何找二面角的平面角?关键是什么?
学生E:在一个平面内选一点A向另一平面作垂线AB,
垂足为B,再过点B向棱a作垂线BO,垂足为O,
连结AO,则∠AOB就是二面角的平面角。
可简记为“两垂一连”。
关键是找或作出其中一个面的垂线
问题5: 在四棱锥P-ABCD中,ABCD是正方形,AC交BD于点O,PA⊥平面ABCD,PA=AB=2,求二面角B—PC—A的正弦值。
学生F上去板书:
解:过B作BE⊥PC,连结OE,
由题4可知BO⊥面PAC,而PC面PAC,
所以BO⊥PC,又BE∩BO=B
所以PC⊥面BEO,EO面BEO
所以PC⊥EO,所以∠BEO是二面角B—PC—A的平面角
在RtPBC中,BO=,
所以
三.体验高考(2012广东高考理18)
如图所示,在四棱锥中,底面为矩形,
平面,点在线段上,平面。
证明:平面;(当成已知条件)
若,求二面角的正切值。
(不展开讲,让学生体验并简单找出平面角就得了)
解:(1)平面,面
平面,面
又面
(2)设AC与BD交点为O,连
∵ OE面BDE ∴ 同理
∴ 为二面角的平面角
∵ AC面PAC ∴
∴ ∴
在,
∴
∴ 二面角的平面角的正切值为3
四.小结:
用几何法求解二面角的步骤?最关键的地方是什么?
学生:一找二证三求,关键是找出二面角的平面角,而找平面角的关键是找或作出其中一个面的垂线。
五.作业:
在四棱锥P-ABCD中,ABCD是平行四边形,PA⊥平面ABCD,PA=AB=a,∠ABC=30°,求二面角P-BC-A的正切值大小。
解:(垂线法)如图PA⊥平面BD 过A作AH⊥BC于H,连结PH则PH⊥BC 又AH⊥BC
故∠PHA是二面角P-BC-A的平面角, 在Rt△ABH中,AH=ABsin∠ABC=aSin30°= 在Rt△PHA中,tan∠PHA=PA/AH=
六.板书设计:
七.教学后记:
八.课后练习
1.在四棱锥P-ABCD中,ABCD为正方形,PA⊥平面ABCD,PA=AB=a,求平面PBA与平面PDC所成二面角的大小为_________________
解(补形化为定义法)如图 将四棱锥P-ABCD补形得正方体ABCD-PQMN,
则PQ⊥PA、PD,于是∠APD是两面所成二面角的平面角。
在Rt△PAD中,PA=AD,则∠APD=45°。
即平面BAP与平面PDC所成二面角的大小为45°
2.(2011广东)在锥体P-ABCD中,ABCD是边长为1的菱形,且∠DAB=60,,PB=2, E,F分别是BC,PC的中点.
(1)证明:AD 平面DEF;
(2) 求二面角P-AD-B的余弦值。
(1)证明:取的中点,连接
∵,∴
∵在边长为1的菱形中,
∴△是等边三角形∴,
∴平面∴
∵分别是的中点∴∥,∥
∴,,∴平面
(2)解:由(1)知,
∴是二面角的平面角
易求得
∴
∴二面角的余弦值为
