第八届“卡西欧”杯全国数学优质课大赛《角的比较和运算》教学设计
文档属性
| 名称 | 第八届“卡西欧”杯全国数学优质课大赛《角的比较和运算》教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 97.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-14 22:41:15 | ||
图片预览



文档简介
《角的比较和运算》教学设计
长春市解放大路学校
李明华
一、教学内容解析
角的比较和运算是在学生学习了角的基本知识之后对角的内容的延续学习,更是对几何图形中有关联的量的认识加深的内容.本节课重点是掌握角的大小比较方法,能进行简单的角的和、差运算;难点是辨析图形中角与角的关系.学好本节课对于学生今后的几何学习有很大的启迪作用.
二、学生学情分析
角的比较和运算是初中七年级上册的内容,学生刚刚开始接触数学中几何部分内容,对于几何学生仅限于对图形的简单认识而不能了解图形中潜在的联系,对于简单的几何逻辑推理语言仅仅在线段相关问题中使用过.借助于本节课内容的传授能够帮助学生建立简单的条件与结论对应的概念,学会使用数学语言描述数学问题本质.
三、教学策略分析
引课
用肢体语言所能展现的几何图形引入新课,让学生意识到数学来源于生活,高于生活,还要最终服务于生活.
角的比较
运用类比的方法让学生学会用已有的知识探知未知的知识,基于学生对线段大小比较方法的掌握,在抛出角的大小比较后,让学生自行寻找角的大小比较方法.希望可以让学生养成良好的数学基本素养,为学生提供思考的空间,养成善于思考,勤于思考的习惯.
归纳,在学生提出比较的方法之后,要培养学生归纳的习惯.数学的灵感来源于不断地对数学知识的归纳,形成自己的数学触感.归纳能力也是学生所要具备的一种基本能力,在教学中我会多引导学生发现、总结,既可以提高学生对数学的探知兴趣还能提高学生归纳的能力,进而增加学生学习数学的能力.
角的和、差
辨析能力的培养,在一个图形中认识几个角之间内在联系为重点,让学生学会把一个式子转化成为多个同等变形的式子,养成学生对同一公式不同表现形式的掌握,认识复杂图形中的内在联系.学会发现一个变化的数学问题中不变的量或关系,并能根据这个量或关系解决相应问题.
培养逻辑推理语言,角平分线的定义中除了让学生能够将定义引申为条件与结论的对应,还要简述几何语言,让学生体会数学逻辑连接词的作用,并且能在今后的学习中学会恰当使用这样的连接词,来阐述数学问题的因果.
课题:4.6.2角的比较和运算
教
学
目
标
知 识
技 能
1.会比较角的大小,掌握角的大小比较方法.
2.理解角的和、差关系,学会辨析图形中角的关系,能够计算角的和、差.
3.理解角的平分线的概念并会辨析图形中角的数量关系.
过 程
方 法
让学生经历从探究两个角的大小比较,三个角的大小比较的过程,归纳出比较角的大小的方法.
经历对角的和、差及角的平分线认知过程,体会图形中位置与数量的关联.
利用角的和差关系,使用三角板中的角画其它度数的角,培养学生发现数学本质的能力.
情 感
态 度
初步体会和掌握用几何知识解决问题的方法,培养学生的识图能力.
教 学 重 点
掌握角的比较方法会比较两个角的大小.
辨析并且准确运算图形中角的和、差.
理解角的平分线的概念并会辨析图形中角的数量关系.
教 学 难 点
1.用类比的方法提炼角的大小比较方法.
2.从图形中抽象出角的关系.
教具与教学手段
为学生准备画好角的透明卡片、三角板、量角器,并利用多媒体配合教学.
教学
环节
教 学 内 容
教学活动
学生活动
设计
意图
引
入
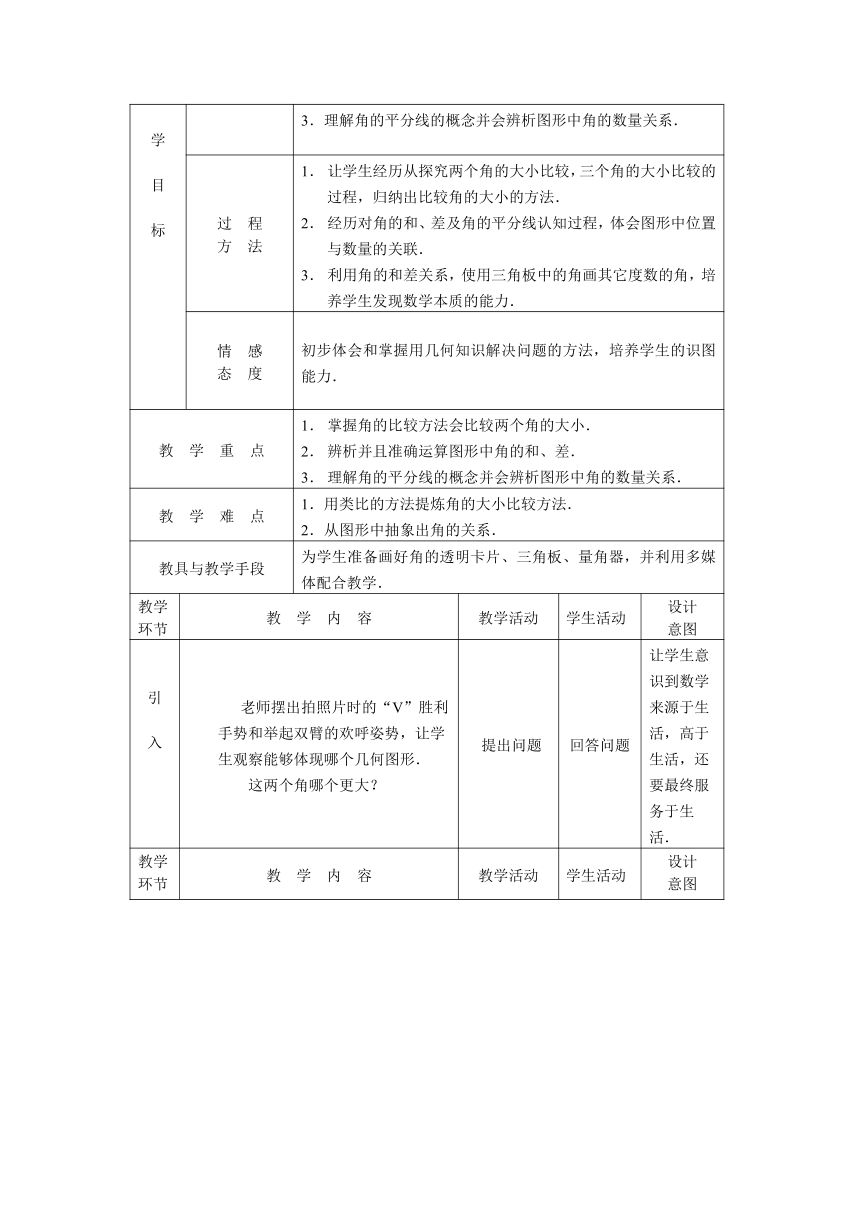
老师摆出拍照片时的“V”胜利手势和举起双臂的欢呼姿势,让学生观察能够体现哪个几何图形.
这两个角哪个更大?
提出问题
回答问题
让学生意识到数学来源于生活,高于生活,还要最终服务于生活.
教学
环节
教 学 内 容
教学活动
学生活动
设计
意图
角
的
比
较
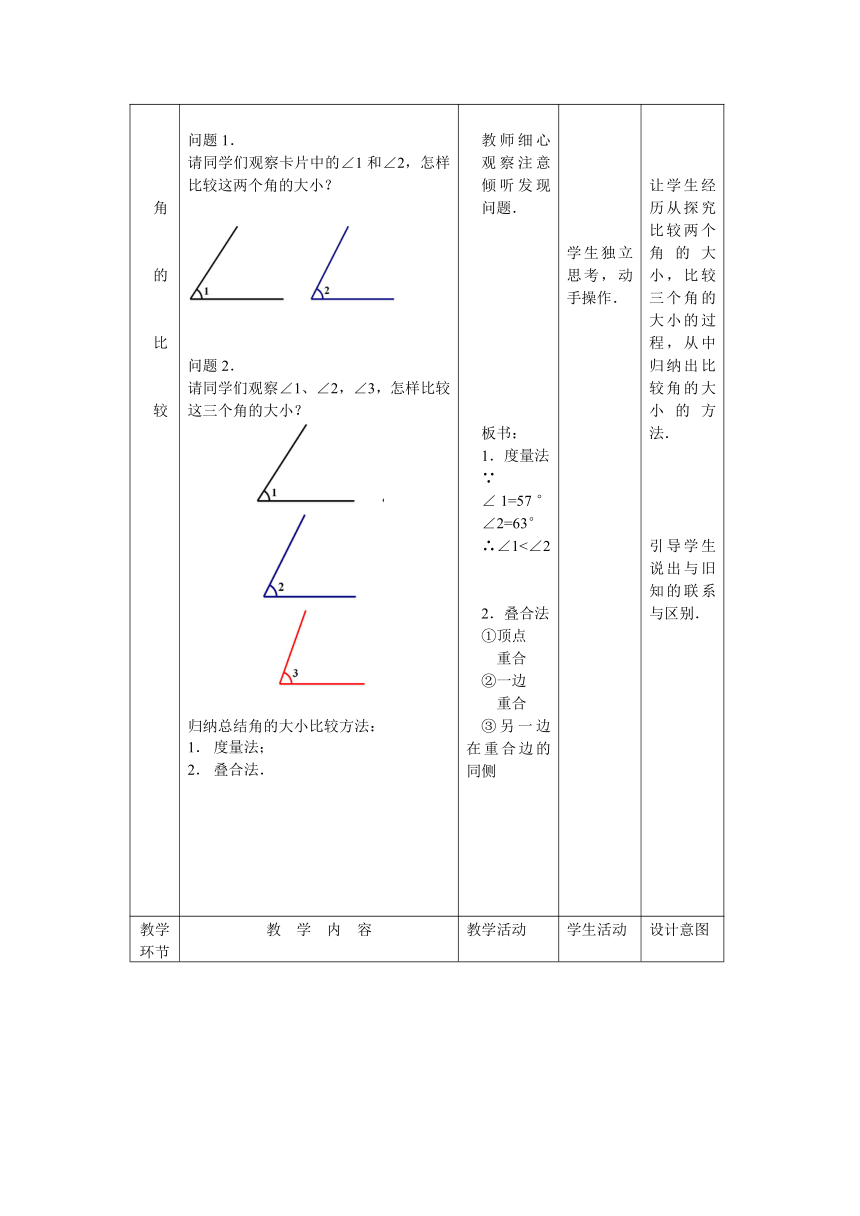
问题1.
请同学们观察卡片中的∠1和∠2,怎样比较这两个角的大小?
问题2.
请同学们观察∠1、∠2,∠3,怎样比较这三个角的大小?
归纳总结角的大小比较方法:
度量法;
叠合法.
教师细心观察注意倾听发现问题.
板书:
1.度量法
∵
∠1=57°∠2=63°
∴∠1<∠2
2.叠合法
①顶点
重合
②一边
重合
③另一边在重合边的同侧
学生独立思考,动手操作.
让学生经历从探究比较两个角的大小,比较三个角的大小的过程,从中归纳出比较角的大小的方法.
引导学生说出与旧知的联系与区别.
教学
环节
教 学 内 容
教学活动
学生活动
设计意图
练
习
先观察图中的两个角,其中哪一个角较大?然后用恰当的方法进行比较,看看你的观察结果是否正确.
学生在学案上作答.教师巡视,及时帮助学生解决困难.
积极参与
并独立度量或作图.
巩固知识,让学生体会,几何问题不能仅仅依靠观察,更需要用科学的方法进行验证.
角
的
和
差
运
算
观察图中的角你能通过此图直接说出哪些角的大小关系?
∠AOC比∠AOB大多少?
得到角之间的等量关系:
∠AOC-∠AOB=∠COB,
∠AOC -∠BOC =∠AOB,
∠AOB+∠COB=∠AOC.
可见,两个角相加或相减,得到的和或差也是角.
教师引导学生发现问题,理解角的和差关系.
独立思考,积极回答.
让学生学会把一个式子转化成为多个同等变形的式子,养成学生对同一公式不同表现形式的掌握,认识复杂图形中的内在联系.
教学
环节
教 学 内 容
教学活动
学生活动
设计意图
练
习
1.如图,若∠AOC=35°,
∠BOC=40°,则∠AOB= 度.
2.如图,若∠AOB= 60°,
∠BOC=40°,则∠AOC= 度.
3.如图,若∠AOB=75°,
∠AOC=60°,则∠BOC= 度.
4.若∠AOB =60°,∠AOC =30°,
则∠BOC = 度.
板书解题
过程:
引导学生口述简单的推理过程.
独立思考
认真解答
学生分析并将结果板演.
培养逻辑推理语言
简述几何语言,让学生体会数学逻辑连接词的作用.
将已知中的图形略去,让学生体会改变已知后给答案带来变化,并注意几何问题中没有给出图形要注意分类讨论.
教学
环节
教 学 内 容
教学活动
学生活动
设计意图
角
的
平
分
线
根据上题中答案之一的图形,∠AOB =60°,∠AOC =30°,∠BOC =30°,引出角平分线的概念.
如果OC是∠AOB的平分线,则它应具备哪些条件?
根据同学们的总结,你能否用几何语言描述图中的角具有怎样的数量关系?
1.∠AOC =∠BOC =∠AOB
2.∠AOB =2∠BOC =2∠AOC
角的平分线概念的几何表示:
∵OC是∠AOB的角平分线,
∴∠AOC =∠BOC =∠AOB
板书:
角的平
分线
根据图形中角的特殊关系归纳角的平分线应满足的条件.
体现由一般到特殊的数学过程,让学生经历总结归纳概念的过程.
再次感受一个等量关系的变形在图形中体现的不同角度.
培养逻辑推理语言
练
习
1.如图,∠AOB=180°,
OC是∠AOB的平分线,
巩固知识
培养逻辑推理语言
教学
环节
教 学 内 容
教学活动
学生活动
设计意图
练
习
则∠AOC= = 度.
2.如图,∠AOC=65°,
OC是∠AOB的平分线,则
∠BOC=∠ = 度;
∠AOB= ∠AOC= 度.
简述几何语言,让学生体会数学逻辑连接词的作用,并且能在今后的学习中学会恰当使用这样的连接词,来阐述数学问题的因果.
思
维
提
升
如图,∠AOB=80°,OC是∠AOB的角平分线,则∠AOC= =40°.
OE、OF分别是∠AOC和∠BOC的平分线,则∠EOF= °.
变式1:
将OC是∠AOB的角平分线的条件删去,
求∠EOF= °.
变式2:
改变OC的位置,求∠EOF= °.
变式3:
改变OB的位置,求∠EOF= °.
通过几何画板软件改变已知条件,动态演示.
从简单的几何模型过渡到复杂的图形,尝试从中抽取基本模型.感受动态几何中变量与不变的量之间的关系.
将最基本的角平分线模型叠加,提出新的问题,一是要让学生再次感受已知条件的改变对结果带来的影响,二是使学生感受动态几何中变化的量与不变的量之间的关系,培养学生几何直觉和模型观念
教学
环节
教 学 内 容
教学活动
学生活动
设计意图
动
手
操
作
你能利用手中的三角板画出15°的角吗?利用手中的三角板还可以画出哪些的角?
动手操作.教师巡视指导.
体会角的和差关系,培养学生的几何直觉和动手操作能力,并从中探究这些角度之间的内在联系.
课
堂
小
结
1.角的比较方法:
①度量法 ②叠合法
2.角的和、差运算
3.角平分线
教师小结
有利于培养归纳、总结的习惯和能力
