1.4空间向量的应用 综合拔高练 同步练习(Word版含解析)
文档属性
| 名称 | 1.4空间向量的应用 综合拔高练 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 467.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览




文档简介
1.4综合拔高练
考点1 用空间向量判断线面位置关系
1.(2019江苏,16,14分,)如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB=BC.求证:
(1)A1B1∥平面DEC1;
(2)BE⊥C1E.
考点2 用空间向量求异面直线所成的角
2.(2019上海,17,14分,)如图,在正三棱锥P-ABC中,PA=PB=PC=2,AB=BC=AC=.
(1)若PB的中点为M,BC的中点为N,求AC与MN的夹角;
(2)求P-ABC的体积.
考点3 用空间向量求直线与平面所成的角
3.(2019天津,17,13分,)如图,AE⊥平面ABCD,CF∥AE,AD∥BC,AD⊥AB,AB=AD=1,AE=BC=2.
(1)求证:BF∥平面ADE;
(2)求直线CE与平面BDE所成角的正弦值;
(3)若二面角E-BD-F的余弦值为,求线段CF的长.
4.(2019浙江,19,15分,)如图,已知三棱柱ABC-A1B1C1,平面A1ACC1⊥平面ABC,∠ABC=90°,∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点.
(1)证明:EF⊥BC;
(2)求直线EF与平面A1BC所成角的余弦值.
考点4 用空间向量求两个平面的夹角
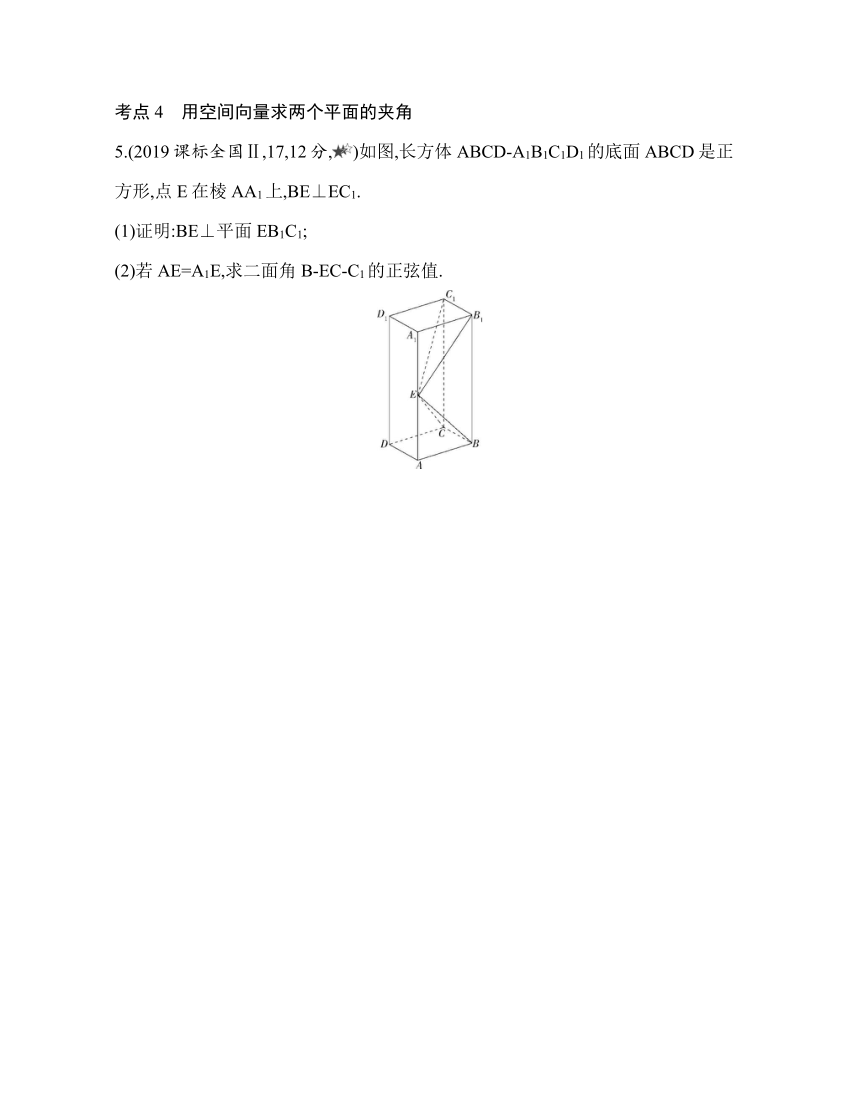
5.(2019课标全国Ⅱ,17,12分,)如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B-EC-C1的正弦值.
6.(2019课标全国Ⅲ,19,12分,)图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角B-CG-A的大小.
考点5 用空间向量求空间距离
7.(2019课标全国Ⅰ,19,12分,)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
考点6 用空间向量解决探索性问题
8.(2019北京,16,14分,)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且=.
(1)求证:CD⊥平面PAD;
(2)求二面角F-AE-P的余弦值;
(3)设点G在PB上,且=.判断直线AG是否在平面AEF内,说明理由.
三年模拟练
应用实践
1.(2020北京通州三模数学试题,)如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=,点E为线段AA1上的点,且AE=.
(1)求证:BE⊥平面ACB1;
(2)求平面ACD1与平面ACB1夹角的余弦值;
(3)判断棱A1B1上是否存在点F,使得直线DF∥平面ACB1,若存在,求线段A1F的长;若不存在,说明理由.深度解析
2.(2020黑龙江哈尔滨师范大学附中高三上期中,)如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,PA⊥底面ABCD,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.
(1)求证:面EMF⊥面PAC;
(2)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求的值.
3.(2020湖南长沙第一中学高三上月考,)如图所示,在梯形ABCD中,AB∥CD,∠BCD=120°,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF.
(1)求证:EF⊥平面BCF;
(2)点M在线段EF上运动,设平面MAB与平面FCB的夹角为θ,试求cos θ的取值范围.
4.(2020山东枣庄部分重点高中高三上,)等边△ABC的边长为3,点D,E分别是边AB,AC上的点,且满足==(如图1).将△ADE沿DE折起到△A1DE的位置,使平面A1DE⊥平面BCED,连接A1B、A1C(如图2).
(1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角为60° 若存在,求出线段BP的长度;若不存在,请说明理由.
答案全解全析
五年高考练
1.证明 (1)取A1C1的中点E1,连接EE1.
由题易得,EC,EB,EE1两两垂直,以E为原点,EC,EB,EE1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,如图.
设AC=2c,AB=1,AA1=a(c>0,a>0).
则E(0,0,0),B(0,,0),D,,0,A1(-c,0,a),B1(0,,a),C1(c,0,a),
所以=(c,,0),=,,0,
所以=2,所以∥,所以A1B1∥ED.
因为ED 平面DEC1,A1B1 平面DEC1,
所以A1B1∥平面DEC1.
(2)由(1)得=(0,,0),=(c,0,a),
而·=0,所以⊥,所以BE⊥C1E.
2.解析 (1)过点P作底面ABC的垂线,垂足为O,则O为底面三角形的中心,连接BO,以O为原点,OB所在直线为x轴,OP所在直线为z轴,过O点平行于AC的直线为y轴,建立空间直角坐标系,则A,C,
M,N.
则=(0,,0),=.
设AC与MN所成角为θ,
则cos θ==,
∴AC与MN的夹角为arccos .
(2)连接AO并延长,交BC于N,则AN=,AO=AN=1,
∴PO==,
∴VP-ABC=××××=.
3.解析 依题意,可以建立以A为原点,,,的方向分别为x轴,y轴,z轴正方向的空间直角坐标系(如图),
可得A(0,0,0),B(1,0,0),C(1,2,0),D(0,1,0),E(0,0,2).
设CF=h(h>0),则F(1,2,h).
(1)证明:依题意,=(1,0,0)是平面ADE的一个法向量,又=(0,2,h),所以·=0,
又因为直线BF 平面ADE,
所以BF∥平面ADE.
(2)依题意,=(-1,1,0),=(-1,0,2),=(-1,-2,2).
设n=(x,y,z)为平面BDE的法向量,
则
即
不妨令z=1,
可得n=(2,2,1),因此有cos<,n>==-.
所以直线CE与平面BDE所成角的正弦值为.
(3)设m=(x1,y1,z1)为平面BDF的法向量,
则
即
不妨令y1=1,可得m=.
由题意,得|cos|===,解得h=.经检验,符合题意.所以线段CF的长为.
4.解析 解法一:(1)证明:连接A1E,因为A1A=A1C,E是AC的中点,所以A1E⊥AC,
又平面A1ACC1⊥平面ABC,A1E 平面A1ACC1,平面A1ACC1∩平面ABC=AC,
所以A1E⊥平面ABC,
则A1E⊥BC.
又因为A1F∥AB,∠ABC=90°,
所以BC⊥A1F.
因为A1E∩A1F=A1,
所以BC⊥平面A1EF.
因此EF⊥BC.
(2)取BC的中点G,连接EG,GF,则四边形EGFA1是平行四边形.
由于A1E⊥平面ABC,故A1E⊥EG,
所以平行四边形EGFA1为矩形.
由(1)得BC⊥平面EGFA1,则平面A1BC⊥平面EGFA1,所以EF在平面A1BC上的射影在直线A1G上.
连接A1G交EF于O,则∠EOG是直线EF与平面A1BC所成的角(或其补角),
不妨设AC=4,则在Rt△A1EG中,A1E=2,EG=.
由于O为A1G的中点,故EO=OG==,
所以cos∠EOG==.
因此,直线EF与平面A1BC所成角的余弦值是.
解法二:(1)证明:连接A1E,因为A1A=A1C,E是AC的中点,所以A1E⊥AC.
又平面A1ACC1⊥平面ABC,A1E 平面A1ACC1,平面A1ACC1∩平面ABC=AC,
所以A1E⊥平面ABC.
如图,以E为原点,分别以射线EC,EA1为y,z轴的正半轴,建立空间直角坐标系Exyz.
不妨设AC=4,则E(0,0,0),A1(0,0,2),B(,1,0),B1(,3,2),F,C(0,2,0).
因此,=,
=(-,1,0).
由·=0得EF⊥BC.
(2)由(1)可得=(0,2,-2).
设平面A1BC的法向量为n=(x,y,z).
由
得
取x=1,则n=(1,,1),
设直线EF与平面A1BC所成角为θ,
则sin θ=|cos<,n>|==.
因此,直线EF与平面A1BC所成角的余弦值为.
5.解析 (1)证明:由已知得,B1C1⊥平面ABB1A1,BE 平面ABB1A1,
故B1C1⊥BE.
又BE⊥EC1,EC1∩B1C1=C1,
所以BE⊥平面EB1C1.
(2)由(1)知∠BEB1=90°.
由题设知Rt△ABE≌Rt△A1B1E,
所以∠AEB=45°,故AE=AB,AA1=2AB.
以D为坐标原点,的方向为x轴正方向,||为单位长,建立如图所示的空间直角坐标系Dxyz,
则C(0,1,0),B(1,1,0),C1(0,1,2),E(1,0,1),所以=(1,0,0),=(1,-1,1),=(0,0,2).
设平面EBC的法向量为n=(x,y,z),
则即
所以可取n=(0,-1,-1).
设平面ECC1的法向量为m=(x1,y1,z1),
则即
所以可取m=(1,1,0).
于是cos==-.
所以二面角B-EC-C1的正弦值为.
6.解析 (1)证明:由已知得AD∥BE,CG∥BE,所以AD∥CG,故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得AB⊥BE,AB⊥BC,BE∩BC=B,
故AB⊥平面BCGE.
又因为AB 平面ABC,
所以平面ABC⊥平面BCGE.
(2)作EH⊥BC,垂足为H.因为EH 平面BCGE,平面BCGE⊥平面ABC,所以EH⊥平面ABC.
由菱形BCGE的边长为2,∠EBC=60°,可求得BH=1,EH=.
以H为坐标原点,的方向为x轴的正方向,建立如图所示的空间直角坐标系Hxyz,
则A(-1,1,0),C(1,0,0),G(2,0,),所以=(1,0,),=(2,-1,0).
设平面ACGD的法向量为n=(x,y,z),
则
即
所以可取n=(3,6,-).
又平面BCGE的法向量可取m=(0,1,0),
所以cos==.
因此二面角B-CG-A的大小为30°.
7.解析 (1)证明:∵直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点,
∴DD1⊥平面ABCD,DE⊥AD,
以D为原点,DA,DE,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,
则M(1,,2),N(1,0,2),D(0,0,0),E(0,,0),C1(-1,,4),所以=(0,-,0),=(-1,,4),=(0,,0),
设平面C1DE的法向量为n=(x,y,z),
则即
取z=1,则n=(4,0,1).
∵·n=0,MN 平面C1DE,
∴MN∥平面C1DE.
(2)由(1)得C(-1,,0),
∴=(-1,,0),
而平面C1DE的一个法向量n=(4,0,1),
∴点C到平面C1DE的距离d===.
8.解析 (1)证明:因为PA⊥平面ABCD,
所以PA⊥CD,
又因为AD⊥CD,PA∩AD=A,
所以CD⊥平面PAD.
(2)过A作AD的垂线交BC于点M.
因为PA⊥平面ABCD,
所以PA⊥AM,PA⊥AD.
如图,建立空间直角坐标系Axyz,则A(0,0,0),B(2,-1,0),C(2,2,0),D(0,2,0),P(0,0,2).
因为E为PD的中点,所以E(0,1,1).
所以=(0,1,1),=(2,2,-2),=(0,0,2).
所以==,
=+=.
设平面AEF的法向量为n=(x,y,z),
则即
令z=1,则y=-1,x=-1.
于是n=(-1,-1,1).
又因为平面PAE的法向量p=(1,0,0),
所以cos==-.
由题知,二面角F-AE-P为锐角,
所以其余弦值为.
(3)直线AG在平面AEF内.理由如下:
因为点G在PB上,且=,=(2,-1,-2),所以==,=+=.
由(2)知,平面AEF的法向量n=(-1,-1,1).
所以·n=-++=0.
所以直线AG在平面AEF内.
三年模拟练
1.解析 (1)证明:因为A1A⊥底面ABCD,
所以A1A⊥AC.
又因为AB⊥AC,A1A∩AB=A,所以AC⊥平面ABB1A1,
又因为BE 平面ABB1A1,所以AC⊥BE.
因为==,∠EAB=∠ABB1=90°,
所以Rt△ABE∽Rt△BB1A,
所以∠ABE=∠AB1B.
因为∠BAB1+∠AB1B=90°,
所以∠BAB1+∠ABE=90°,
所以BE⊥AB1.
又AC∩AB1=A,所以BE⊥平面ACB1.
(2)易得AC⊥AB.如图,以A为原点建立空间直角坐标系,
依题意可得A(0,0,0),B(0,1,0),C(2,0,0),D(1,-2,0),D1(1,-2,2),E.
由(1)知,BE⊥平面ACB1,则=为平面ACB1的一个法向量,设n=(x,y,z)为平面ACD1的法向量.
由=(1,-2,2),=(2,0,0),
得即
不妨设z=1,可得n=(0,1,1).
因此|cos|==.
所以平面ACD1与平面ACB1夹角的余弦值为.
(3)设A1F=a(0≤a≤1),则F(0,a,2),=(-1,a+2,2).
·=(-1,a+2,2)·=a+2-1=0,解得a=-1(舍去).
所以直线DF的方向向量与平面ACB1的法向量不垂直,
所以棱A1B1上不存在点F,使直线DF∥平面ACB1.
解题反思 本题主要考查线面垂直、线面平行以及面面夹角的问题,熟记线面垂直的判定定理以及用空间向量的方法求面面夹角即可,属于常考题型.
2.解析 (1)证明:∵PA⊥面ABCD,EF 面ABCD,∴EF⊥AP.
在△ABC中,AB=AC,∠ABC=∠ACB=45°,∴AB⊥AC,
又AF∥BE,且AF=BE,∴四边形ABEF为平行四边形,∴AB∥EF,因此AC⊥EF,又AP∩AC=A,AP 面PAC,AC 面PAC,
∴EF⊥面PAC,
又EF 面EMF,∴面EMF⊥面PAC.
(2)分别以AE,AD,AP为x轴,y轴,z轴,建立空间直角坐标系Axyz,则B(,-,0),C(,,0),P(0,0,2),D(0,2,0),E(,0,0),∴=(,,-2),=(0,2,0),=(0,2,-2),=(,0,-2).
设平面PBC的法向量为n=(x,y,z),
则
令z=1,则x=,∴n=(,0,1),
易知平面ABCD的一个法向量m=(0,0,1).设=λ,λ∈[0,1],
则=λ=λ(0,2,-2),
∴=-=(,-2λ,-2+2λ).
∵直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,
∴|cos<,n>|=|cos<,m>|,
即=,
即=,解得λ=,故=λ=.
3.解析 (1)证明:连接AC,设AD=CD=BC=1,
∵AB∥CD,∠BCD=120°,∴AB=2,∠ABC=60°,
∴AC2=AB2+BC2-2AB·BC·cos 60°=3,
∴AB2=AC2+BC2,∴BC⊥AC.
∵四边形ACFE为矩形,∴AC⊥CF.
∵CF,BC 平面BCF,且CF∩BC=C,
∴AC⊥平面BCF.
∵EF∥AC,∴EF⊥平面BCF.
(2)以C为坐标原点,直线CA,CB,CF分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
令FM=λ(0≤λ≤),则A(,0,0),B(0,1,0),M(λ,0,1),
所以=(-,1,0),=(λ,-1,1),
设n1=(x,y,z)为平面MAB的法向量,
由得
取x=1,所以n1=(1,,-λ).
因为n2=(1,0,0)是平面FCB的一个法向量,所以cos θ===.
因为0≤λ≤,所以当λ=0时,cos θ有最小值;当λ=时,cos θ有最大值,
所以cos θ∈.
4.解析 (1)证明:在△ADE中,AD=1,AE=2,∠A=60°,
得DE==,
所以AD2+DE2=AE2,从而AD⊥DE,
所以在题图2中,A1D⊥DE.
又平面A1DE⊥平面BCED,平面A1DE∩平面BCED=DE,A1D 平面A1DE,
所以A1D⊥平面BCED.
(2)由(1)知,A1D,DB,DE两两垂直,以DB,DE,DA1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.
则B(2,0,0),A1(0,0,1),C,
则=,=(2,0,-1),
假设线段BC上存在点P,使直线PA1与平面A1BD所成的角为60°,
设=λ=,其中λ∈[0,1],
则=+=.
易知平面A1BD的一个法向量n=(0,1,0),
则sin 60°=|cos<,n>|=
==.
解得λ=,此时||=||=.
所以存在满足要求的点P,且线段BP的长度为.
考点1 用空间向量判断线面位置关系
1.(2019江苏,16,14分,)如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB=BC.求证:
(1)A1B1∥平面DEC1;
(2)BE⊥C1E.
考点2 用空间向量求异面直线所成的角
2.(2019上海,17,14分,)如图,在正三棱锥P-ABC中,PA=PB=PC=2,AB=BC=AC=.
(1)若PB的中点为M,BC的中点为N,求AC与MN的夹角;
(2)求P-ABC的体积.
考点3 用空间向量求直线与平面所成的角
3.(2019天津,17,13分,)如图,AE⊥平面ABCD,CF∥AE,AD∥BC,AD⊥AB,AB=AD=1,AE=BC=2.
(1)求证:BF∥平面ADE;
(2)求直线CE与平面BDE所成角的正弦值;
(3)若二面角E-BD-F的余弦值为,求线段CF的长.
4.(2019浙江,19,15分,)如图,已知三棱柱ABC-A1B1C1,平面A1ACC1⊥平面ABC,∠ABC=90°,∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点.
(1)证明:EF⊥BC;
(2)求直线EF与平面A1BC所成角的余弦值.
考点4 用空间向量求两个平面的夹角
5.(2019课标全国Ⅱ,17,12分,)如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B-EC-C1的正弦值.
6.(2019课标全国Ⅲ,19,12分,)图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角B-CG-A的大小.
考点5 用空间向量求空间距离
7.(2019课标全国Ⅰ,19,12分,)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
考点6 用空间向量解决探索性问题
8.(2019北京,16,14分,)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且=.
(1)求证:CD⊥平面PAD;
(2)求二面角F-AE-P的余弦值;
(3)设点G在PB上,且=.判断直线AG是否在平面AEF内,说明理由.
三年模拟练
应用实践
1.(2020北京通州三模数学试题,)如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=,点E为线段AA1上的点,且AE=.
(1)求证:BE⊥平面ACB1;
(2)求平面ACD1与平面ACB1夹角的余弦值;
(3)判断棱A1B1上是否存在点F,使得直线DF∥平面ACB1,若存在,求线段A1F的长;若不存在,说明理由.深度解析
2.(2020黑龙江哈尔滨师范大学附中高三上期中,)如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,PA⊥底面ABCD,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.
(1)求证:面EMF⊥面PAC;
(2)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求的值.
3.(2020湖南长沙第一中学高三上月考,)如图所示,在梯形ABCD中,AB∥CD,∠BCD=120°,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF.
(1)求证:EF⊥平面BCF;
(2)点M在线段EF上运动,设平面MAB与平面FCB的夹角为θ,试求cos θ的取值范围.
4.(2020山东枣庄部分重点高中高三上,)等边△ABC的边长为3,点D,E分别是边AB,AC上的点,且满足==(如图1).将△ADE沿DE折起到△A1DE的位置,使平面A1DE⊥平面BCED,连接A1B、A1C(如图2).
(1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角为60° 若存在,求出线段BP的长度;若不存在,请说明理由.
答案全解全析
五年高考练
1.证明 (1)取A1C1的中点E1,连接EE1.
由题易得,EC,EB,EE1两两垂直,以E为原点,EC,EB,EE1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,如图.
设AC=2c,AB=1,AA1=a(c>0,a>0).
则E(0,0,0),B(0,,0),D,,0,A1(-c,0,a),B1(0,,a),C1(c,0,a),
所以=(c,,0),=,,0,
所以=2,所以∥,所以A1B1∥ED.
因为ED 平面DEC1,A1B1 平面DEC1,
所以A1B1∥平面DEC1.
(2)由(1)得=(0,,0),=(c,0,a),
而·=0,所以⊥,所以BE⊥C1E.
2.解析 (1)过点P作底面ABC的垂线,垂足为O,则O为底面三角形的中心,连接BO,以O为原点,OB所在直线为x轴,OP所在直线为z轴,过O点平行于AC的直线为y轴,建立空间直角坐标系,则A,C,
M,N.
则=(0,,0),=.
设AC与MN所成角为θ,
则cos θ==,
∴AC与MN的夹角为arccos .
(2)连接AO并延长,交BC于N,则AN=,AO=AN=1,
∴PO==,
∴VP-ABC=××××=.
3.解析 依题意,可以建立以A为原点,,,的方向分别为x轴,y轴,z轴正方向的空间直角坐标系(如图),
可得A(0,0,0),B(1,0,0),C(1,2,0),D(0,1,0),E(0,0,2).
设CF=h(h>0),则F(1,2,h).
(1)证明:依题意,=(1,0,0)是平面ADE的一个法向量,又=(0,2,h),所以·=0,
又因为直线BF 平面ADE,
所以BF∥平面ADE.
(2)依题意,=(-1,1,0),=(-1,0,2),=(-1,-2,2).
设n=(x,y,z)为平面BDE的法向量,
则
即
不妨令z=1,
可得n=(2,2,1),因此有cos<,n>==-.
所以直线CE与平面BDE所成角的正弦值为.
(3)设m=(x1,y1,z1)为平面BDF的法向量,
则
即
不妨令y1=1,可得m=.
由题意,得|cos
4.解析 解法一:(1)证明:连接A1E,因为A1A=A1C,E是AC的中点,所以A1E⊥AC,
又平面A1ACC1⊥平面ABC,A1E 平面A1ACC1,平面A1ACC1∩平面ABC=AC,
所以A1E⊥平面ABC,
则A1E⊥BC.
又因为A1F∥AB,∠ABC=90°,
所以BC⊥A1F.
因为A1E∩A1F=A1,
所以BC⊥平面A1EF.
因此EF⊥BC.
(2)取BC的中点G,连接EG,GF,则四边形EGFA1是平行四边形.
由于A1E⊥平面ABC,故A1E⊥EG,
所以平行四边形EGFA1为矩形.
由(1)得BC⊥平面EGFA1,则平面A1BC⊥平面EGFA1,所以EF在平面A1BC上的射影在直线A1G上.
连接A1G交EF于O,则∠EOG是直线EF与平面A1BC所成的角(或其补角),
不妨设AC=4,则在Rt△A1EG中,A1E=2,EG=.
由于O为A1G的中点,故EO=OG==,
所以cos∠EOG==.
因此,直线EF与平面A1BC所成角的余弦值是.
解法二:(1)证明:连接A1E,因为A1A=A1C,E是AC的中点,所以A1E⊥AC.
又平面A1ACC1⊥平面ABC,A1E 平面A1ACC1,平面A1ACC1∩平面ABC=AC,
所以A1E⊥平面ABC.
如图,以E为原点,分别以射线EC,EA1为y,z轴的正半轴,建立空间直角坐标系Exyz.
不妨设AC=4,则E(0,0,0),A1(0,0,2),B(,1,0),B1(,3,2),F,C(0,2,0).
因此,=,
=(-,1,0).
由·=0得EF⊥BC.
(2)由(1)可得=(0,2,-2).
设平面A1BC的法向量为n=(x,y,z).
由
得
取x=1,则n=(1,,1),
设直线EF与平面A1BC所成角为θ,
则sin θ=|cos<,n>|==.
因此,直线EF与平面A1BC所成角的余弦值为.
5.解析 (1)证明:由已知得,B1C1⊥平面ABB1A1,BE 平面ABB1A1,
故B1C1⊥BE.
又BE⊥EC1,EC1∩B1C1=C1,
所以BE⊥平面EB1C1.
(2)由(1)知∠BEB1=90°.
由题设知Rt△ABE≌Rt△A1B1E,
所以∠AEB=45°,故AE=AB,AA1=2AB.
以D为坐标原点,的方向为x轴正方向,||为单位长,建立如图所示的空间直角坐标系Dxyz,
则C(0,1,0),B(1,1,0),C1(0,1,2),E(1,0,1),所以=(1,0,0),=(1,-1,1),=(0,0,2).
设平面EBC的法向量为n=(x,y,z),
则即
所以可取n=(0,-1,-1).
设平面ECC1的法向量为m=(x1,y1,z1),
则即
所以可取m=(1,1,0).
于是cos
所以二面角B-EC-C1的正弦值为.
6.解析 (1)证明:由已知得AD∥BE,CG∥BE,所以AD∥CG,故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得AB⊥BE,AB⊥BC,BE∩BC=B,
故AB⊥平面BCGE.
又因为AB 平面ABC,
所以平面ABC⊥平面BCGE.
(2)作EH⊥BC,垂足为H.因为EH 平面BCGE,平面BCGE⊥平面ABC,所以EH⊥平面ABC.
由菱形BCGE的边长为2,∠EBC=60°,可求得BH=1,EH=.
以H为坐标原点,的方向为x轴的正方向,建立如图所示的空间直角坐标系Hxyz,
则A(-1,1,0),C(1,0,0),G(2,0,),所以=(1,0,),=(2,-1,0).
设平面ACGD的法向量为n=(x,y,z),
则
即
所以可取n=(3,6,-).
又平面BCGE的法向量可取m=(0,1,0),
所以cos
因此二面角B-CG-A的大小为30°.
7.解析 (1)证明:∵直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点,
∴DD1⊥平面ABCD,DE⊥AD,
以D为原点,DA,DE,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,
则M(1,,2),N(1,0,2),D(0,0,0),E(0,,0),C1(-1,,4),所以=(0,-,0),=(-1,,4),=(0,,0),
设平面C1DE的法向量为n=(x,y,z),
则即
取z=1,则n=(4,0,1).
∵·n=0,MN 平面C1DE,
∴MN∥平面C1DE.
(2)由(1)得C(-1,,0),
∴=(-1,,0),
而平面C1DE的一个法向量n=(4,0,1),
∴点C到平面C1DE的距离d===.
8.解析 (1)证明:因为PA⊥平面ABCD,
所以PA⊥CD,
又因为AD⊥CD,PA∩AD=A,
所以CD⊥平面PAD.
(2)过A作AD的垂线交BC于点M.
因为PA⊥平面ABCD,
所以PA⊥AM,PA⊥AD.
如图,建立空间直角坐标系Axyz,则A(0,0,0),B(2,-1,0),C(2,2,0),D(0,2,0),P(0,0,2).
因为E为PD的中点,所以E(0,1,1).
所以=(0,1,1),=(2,2,-2),=(0,0,2).
所以==,
=+=.
设平面AEF的法向量为n=(x,y,z),
则即
令z=1,则y=-1,x=-1.
于是n=(-1,-1,1).
又因为平面PAE的法向量p=(1,0,0),
所以cos
由题知,二面角F-AE-P为锐角,
所以其余弦值为.
(3)直线AG在平面AEF内.理由如下:
因为点G在PB上,且=,=(2,-1,-2),所以==,=+=.
由(2)知,平面AEF的法向量n=(-1,-1,1).
所以·n=-++=0.
所以直线AG在平面AEF内.
三年模拟练
1.解析 (1)证明:因为A1A⊥底面ABCD,
所以A1A⊥AC.
又因为AB⊥AC,A1A∩AB=A,所以AC⊥平面ABB1A1,
又因为BE 平面ABB1A1,所以AC⊥BE.
因为==,∠EAB=∠ABB1=90°,
所以Rt△ABE∽Rt△BB1A,
所以∠ABE=∠AB1B.
因为∠BAB1+∠AB1B=90°,
所以∠BAB1+∠ABE=90°,
所以BE⊥AB1.
又AC∩AB1=A,所以BE⊥平面ACB1.
(2)易得AC⊥AB.如图,以A为原点建立空间直角坐标系,
依题意可得A(0,0,0),B(0,1,0),C(2,0,0),D(1,-2,0),D1(1,-2,2),E.
由(1)知,BE⊥平面ACB1,则=为平面ACB1的一个法向量,设n=(x,y,z)为平面ACD1的法向量.
由=(1,-2,2),=(2,0,0),
得即
不妨设z=1,可得n=(0,1,1).
因此|cos
所以平面ACD1与平面ACB1夹角的余弦值为.
(3)设A1F=a(0≤a≤1),则F(0,a,2),=(-1,a+2,2).
·=(-1,a+2,2)·=a+2-1=0,解得a=-1(舍去).
所以直线DF的方向向量与平面ACB1的法向量不垂直,
所以棱A1B1上不存在点F,使直线DF∥平面ACB1.
解题反思 本题主要考查线面垂直、线面平行以及面面夹角的问题,熟记线面垂直的判定定理以及用空间向量的方法求面面夹角即可,属于常考题型.
2.解析 (1)证明:∵PA⊥面ABCD,EF 面ABCD,∴EF⊥AP.
在△ABC中,AB=AC,∠ABC=∠ACB=45°,∴AB⊥AC,
又AF∥BE,且AF=BE,∴四边形ABEF为平行四边形,∴AB∥EF,因此AC⊥EF,又AP∩AC=A,AP 面PAC,AC 面PAC,
∴EF⊥面PAC,
又EF 面EMF,∴面EMF⊥面PAC.
(2)分别以AE,AD,AP为x轴,y轴,z轴,建立空间直角坐标系Axyz,则B(,-,0),C(,,0),P(0,0,2),D(0,2,0),E(,0,0),∴=(,,-2),=(0,2,0),=(0,2,-2),=(,0,-2).
设平面PBC的法向量为n=(x,y,z),
则
令z=1,则x=,∴n=(,0,1),
易知平面ABCD的一个法向量m=(0,0,1).设=λ,λ∈[0,1],
则=λ=λ(0,2,-2),
∴=-=(,-2λ,-2+2λ).
∵直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,
∴|cos<,n>|=|cos<,m>|,
即=,
即=,解得λ=,故=λ=.
3.解析 (1)证明:连接AC,设AD=CD=BC=1,
∵AB∥CD,∠BCD=120°,∴AB=2,∠ABC=60°,
∴AC2=AB2+BC2-2AB·BC·cos 60°=3,
∴AB2=AC2+BC2,∴BC⊥AC.
∵四边形ACFE为矩形,∴AC⊥CF.
∵CF,BC 平面BCF,且CF∩BC=C,
∴AC⊥平面BCF.
∵EF∥AC,∴EF⊥平面BCF.
(2)以C为坐标原点,直线CA,CB,CF分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
令FM=λ(0≤λ≤),则A(,0,0),B(0,1,0),M(λ,0,1),
所以=(-,1,0),=(λ,-1,1),
设n1=(x,y,z)为平面MAB的法向量,
由得
取x=1,所以n1=(1,,-λ).
因为n2=(1,0,0)是平面FCB的一个法向量,所以cos θ===.
因为0≤λ≤,所以当λ=0时,cos θ有最小值;当λ=时,cos θ有最大值,
所以cos θ∈.
4.解析 (1)证明:在△ADE中,AD=1,AE=2,∠A=60°,
得DE==,
所以AD2+DE2=AE2,从而AD⊥DE,
所以在题图2中,A1D⊥DE.
又平面A1DE⊥平面BCED,平面A1DE∩平面BCED=DE,A1D 平面A1DE,
所以A1D⊥平面BCED.
(2)由(1)知,A1D,DB,DE两两垂直,以DB,DE,DA1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.
则B(2,0,0),A1(0,0,1),C,
则=,=(2,0,-1),
假设线段BC上存在点P,使直线PA1与平面A1BD所成的角为60°,
设=λ=,其中λ∈[0,1],
则=+=.
易知平面A1BD的一个法向量n=(0,1,0),
则sin 60°=|cos<,n>|=
==.
解得λ=,此时||=||=.
所以存在满足要求的点P,且线段BP的长度为.
