第一章专题强化练2 空间向量与立体几何的综合应用 同步练习(Word版含解析)
文档属性
| 名称 | 第一章专题强化练2 空间向量与立体几何的综合应用 同步练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 307.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 15:19:34 | ||
图片预览




文档简介
专题强化练2 空间向量与立体几何的综合应用
解答题
1.(2020陕西西安中学高二月考,)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
(1)求证:BD⊥平面PAC;
(2)若PA=AB,求PB与AC所成角的余弦值.
2.(2020安徽合肥六中高二上期末,)如图,在直三棱柱A1B1C1-ABC中,AC⊥AB,AC=AB=4,AA1=6,点E、F分别为CA1、AB的中点.
(1)证明:EF∥平面BCC1B1;
(2)求B1F与平面AEF所成角的正弦值.
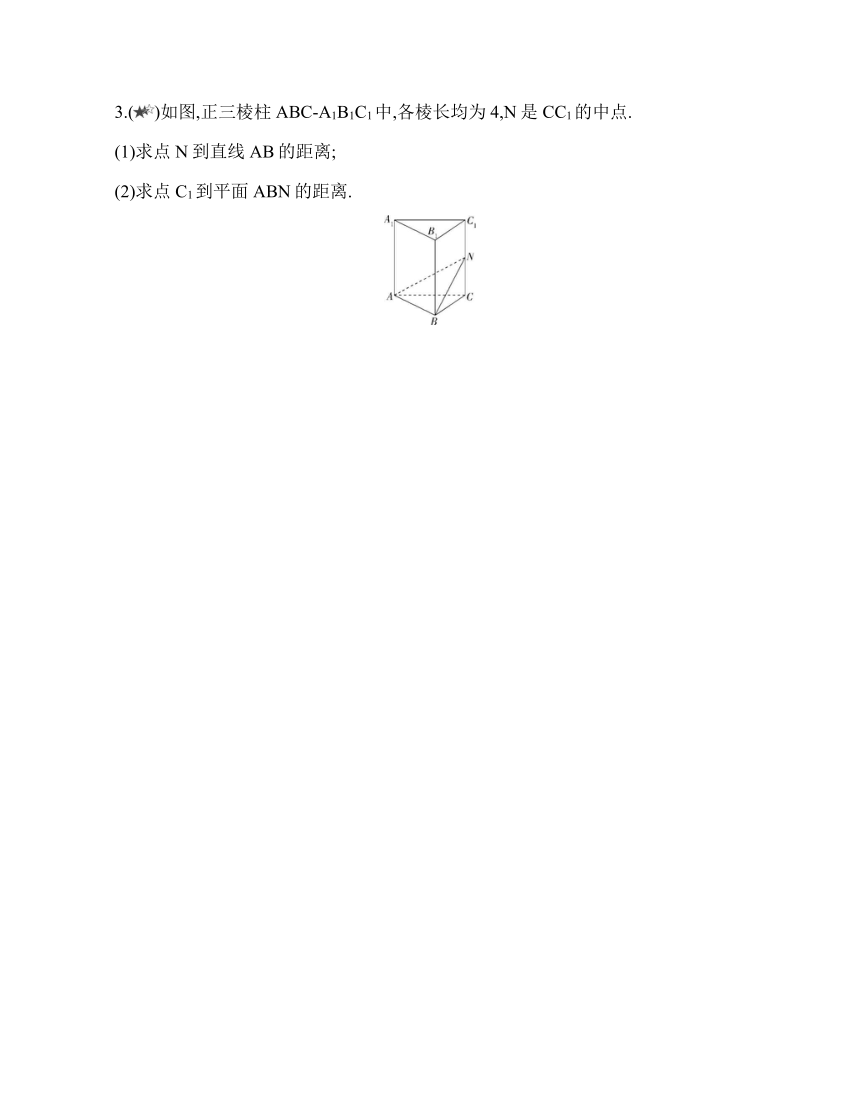
3.()如图,正三棱柱ABC-A1B1C1中,各棱长均为4,N是CC1的中点.
(1)求点N到直线AB的距离;
(2)求点C1到平面ABN的距离.
4.(2020山东烟台第一中学高三上联考,)如图所示的几何体中,BE⊥BC,EA⊥AC,BC=2,AC=2,∠ACB=45°,AD∥BC,BC=2AD.
(1)求证:AE⊥平面ABCD;
(2)若∠ABE=60°,点F在EC上,且满足EF=2FC,求平面FAD与平面ADC的夹角的余弦值.
5.()如图,一个正三角形ABC'和一个平行四边形ABDE在同一个平面内,其中AB=8,BD=AD=,AB,DE的中点分别为F,G.现沿直线AB将△ABC'翻折成△ABC,使二面角C-AB-D为120°,设CE的中点为H.
(1)求证:平面CDF∥平面AGH;
(2)求异面直线AB与CE所成角的正切值;
(3)求平面CDE与平面DEF的夹角的余弦值.
6.(2020重庆西南大学附中高二上期末,)如图,四棱锥P-ABCD中,底面ABCD为矩形,侧面PAD为正三角形,AD=2,AB=3,平面PAD⊥平面ABCD,E为棱PB上一点(不与P、B重合),平面ADE交棱PC于点F.
(1)求证:AD∥EF;
(2)若平面BAC与平面ACE夹角的余弦值为,求点B到平面AEC的距离.
7.()如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点.
(1)求异面直线AC与PB间的距离;
(2)在侧面PAB内找一点N,使NE⊥平面PAC,并求出N到AB和AP的距离.
8.(2020河南河大附中高二上期末,)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求平面DAE与平面AEC夹角的余弦值.深度解析
答案全解全析
解答题
1.解析 (1)证明:因为四边形ABCD是菱形,
所以AC⊥BD.
因为PA⊥平面ABCD,BD 平面ABCD,
所以PA⊥BD.
又因为AC∩PA=A,所以BD⊥平面PAC.
(2)设AC∩BD=O.
因为∠BAD=60°,AB=2,
所以BO=1,AO=CO=.
如图,以O为坐标原点,直线OB,OC分别为x轴,y轴,过点O平行于PA的直线为z轴,建立空间直角坐标系Oxyz,
则P(0,-,2),A(0,-,0),B(1,0,0),C(0,,0),
所以=(1,,-2),=(0,2,0).
设PB与AC所成角为θ,
则cos θ===,
即PB与AC所成角的余弦值为.
2.解析 (1)证明:如图,连接EC1、BC1,
因为三棱柱A1B1C1-ABC为直三棱柱,
所以E为AC1的中点.
又因为F为AB的中点,所以EF∥BC1.
又EF 平面BCC1B1,BC1 平面BCC1B1,所以EF∥平面BCC1B1.
(2)以A1为原点,A1C1、A1B1、A1A所在直线分别为x、y、z轴,建立如图所示的空间直角坐标系A1xyz,
则A(0,0,6),B1(0,4,0),E(2,0,3),F(0,2,6),
所以=(0,-2,6),=(2,0,-3),=(0,2,0),
设平面AEF的法向量为n=(x,y,z),则
令x=3,得n=(3,0,2),
记B1F与平面AEF所成角为θ,则sin θ=|cos<,n>|==.
3.解析 建立如图所示的空间直角坐标系,
则A(0,0,0),B(2,2,0),C(0,4,0),C1(0,4,4),∵N是CC1的中点,∴N(0,4,2).
(1)=(0,4,2),=(2,2,0),则||=2,||=4.设点N到直线AB的距离为d1,
则d1===4.
(2)设平面ABN的法向量为n=(x,y,z),则由n⊥,n⊥,
得令z=2,则y=-1,x=,即n=.
易知=(0,0,-2),设点C1到平面ABN的距离为d2,
则d2===.
4.解析 (1)证明:在△ABC中,BC=2,AC=2,∠ACB=45°,
由余弦定理可得AB2=BC2+AC2-2×BC×AC×cos 45°=4,所以AB=2(负值舍去),
因为AC2=AB2+BC2,
所以△ABC是直角三角形,AB⊥BC.
又BE⊥BC,AB∩BE=B,
所以BC⊥平面ABE.
因为AE 平面ABE,所以BC⊥AE,
因为EA⊥AC,AC∩BC=C,
所以AE⊥平面ABCD.
(2)由题易得EB=2AB=4,由(1)知,BC⊥平面ABE,所以平面BEC⊥平面ABE,如图,以B为原点,过点B且垂直于平面BEC的直线为z轴,BE,BC所在直线分别为x,y轴,建立空间直角坐标系Bxyz,则C(0,2,0),E(4,0,0),A(1,0,),D(1,1,),
因为EF=2FC,所以F,
易知=(0,1,0),=,
设平面FAD的法向量为n=(x,y,z),
则
即
令z=,则x=9,所以n=(9,0,).
由(1)知EA⊥平面ABCD,所以=(-3,0,)为平面ABCD的一个法向量.
设平面FAD与平面ADC的夹角为α,
则cos α===,
所以平面FAD与平面ADC的夹角的余弦值为.
5.解析 (1)证明:因为四边形ABDE为平行四边形,F、G分别为AB、DE的中点,
所以四边形FDGA为平行四边形,
所以FD∥AG.
又H、G分别为CE、DE的中点,
所以HG∥CD.
因为FD、CD 平面AGH,AG、HG 平面AGH,所以FD∥平面AGH,CD∥平面AGH,因为FD、CD 平面CDF,FD∩CD=D,所以平面CDF∥平面AGH.
(2)因为三角形ABC为正三角形,BD=AD,F为AB的中点,所以AB⊥CF,AB⊥DF,所以∠CFD为二面角C-AB-D的平面角,又CF∩DF=F,所以AB⊥平面CFD,因为AB 平面ABDE,所以平面CFD⊥平面ABDE.
作CO⊥平面ABDE于O,则O在直线DF上.又二面角C-AB-D的平面角为∠CFD=120°,所以O在线段DF的延长线上.易知CF=4,则FO=2,CO=6.
以F为原点,FD、FA所在直线分别为x轴、y轴,过点F平行于OC的直线为z轴,建立空间直角坐标系,如图,
则A(0,4,0),B(0,-4,0),D(3,0,0),E(3,8,0),C(-2,0,6),
所以=(0,-8,0),=(5,8,-6).
所以异面直线AB与CE所成角的余弦值为|cos<,>|===,
从而其正切值为=.
(3)由(2)知=(5,0,-6),=(0,8,0),设平面CDE的法向量为n1=(x,y,z),则由n1⊥,n1⊥得
令z=5,得n1=(6,0,5).
易知平面DEF的一个法向量n2=(0,0,1),所以平面CDE与平面DEF的夹角的余弦值为|cos|==.
6.解析 (1)证明:∵底面ABCD为矩形,
∴AD∥BC,
又∵AD 平面PBC,BC 平面PBC,
∴AD∥平面PBC.
又∵AD 平面ADE,平面ADE∩平面PBC=EF,∴AD∥EF.
(2)如图,取AD的中点O,连接PO,过点O作OH∥AB交BC于点H.
∵侧面PAD为正三角形,∴PO⊥AD,
∵平面PAD⊥平面ABCD,且交线为AD,
∴PO⊥平面ABCD,∵底面ABCD为矩形,∴AB⊥AD,∴OH⊥AD.
以O为原点,OA,OH,OP所在直线分别为x轴,y轴,z轴建立空间直角坐标系Oxyz,
则O(0,0,0),P(0,0,),A(1,0,0),B(1,3,0),C(-1,3,0),∴=(1,3,-),=(-2,3,0).
设=λ(0<λ<1),
则E(λ,3λ,-λ),
∴=(λ-1,3λ,-λ).
设平面AEC的法向量为n=(x1,y1,z1),
则
令x1=3,则y1=2,z1=.
∴平面AEC的一个法向量为n=.
易知=(0,0,)是平面ABC的一个法向量.
∴|cos<,n>|=
==,
解得λ=,∴E,
∴=.
又∵平面AEC的一个法向量n=(3,2,-3 ),
∴点B到平面AEC的距离为==.
7.解析 (1)由题意得AB⊥AD,PA⊥AD,PA⊥AB.
以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,建立空间直角坐标系,如图,
则A(0,0,0),C(,1,0),P(0,0,2),B(,0,0),
∴=(,1,0),=(,0,-2),=(0,0,2),
设异面直线AC、PB的公垂线的方向向量为n=(x,y,z),则n⊥,n⊥,
∴令x=1,则y=-,z=,即n=.
设异面直线AC、PB之间的距离为d,
则d===.
(2)设在侧面PAB内存在一点N(a,0,c),使NE⊥平面PAC,
由(1)知E,
∴=,
∴
解得∴N,
∴N到AB的距离为1,N 到AP的距离为.
8.解析 (1)证明:由题意可得,△ABD≌△CBD,从而AD=DC.
又△ACD是直角三角形,所以∠ADC=90°.
如图,取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO.
又△ABC是正三角形,所以BO⊥AC.
所以∠DOB为二面角D-AC-B的平面角.
在Rt△AOB中,BO2+AO2=AB2.
又AB=BD,所以BO2+DO2=BO2+AO2=AB2=BD2,
故∠DOB=90°.
所以平面ACD⊥平面ABC.
(2)由题设及(1)知,OA,OB,OD两两垂直,以O为坐标原点,,,的方向分别为x轴,y轴,z轴正方向,||为单位长,建立如图所示的空间直角坐标系Oxyz,则A(1,0,0),B(0,,0),C(-1,0,0),D(0,0,1).
由题设知,四面体ABCE的体积为四面体ABCD的体积的,从而E到平面ABC的距离为D到平面ABC的距离的,即E为DB的中点,得E.
故=(-1,0,1),=(-2,0,0),=.
设n=(x,y,z)是平面DAE的法向量,则即
可取n=.
设m是平面AEC的法向量,则同理可取m=(0,-1,),
则|cos|==.
所以平面DAE与平面AEC夹角的余弦值为.
解题反思 (1)求解本题要注意两点:一是两平面的法向量的夹角不一定是所求的两个平面的夹角;二是利用方程思想进行向量运算时,要认真细心,准确计算.(2)设m,n分别为平面α,β的法向量,则两个平面的夹角θ与互补或相等,故有
cos θ=|cos|=.
解答题
1.(2020陕西西安中学高二月考,)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
(1)求证:BD⊥平面PAC;
(2)若PA=AB,求PB与AC所成角的余弦值.
2.(2020安徽合肥六中高二上期末,)如图,在直三棱柱A1B1C1-ABC中,AC⊥AB,AC=AB=4,AA1=6,点E、F分别为CA1、AB的中点.
(1)证明:EF∥平面BCC1B1;
(2)求B1F与平面AEF所成角的正弦值.
3.()如图,正三棱柱ABC-A1B1C1中,各棱长均为4,N是CC1的中点.
(1)求点N到直线AB的距离;
(2)求点C1到平面ABN的距离.
4.(2020山东烟台第一中学高三上联考,)如图所示的几何体中,BE⊥BC,EA⊥AC,BC=2,AC=2,∠ACB=45°,AD∥BC,BC=2AD.
(1)求证:AE⊥平面ABCD;
(2)若∠ABE=60°,点F在EC上,且满足EF=2FC,求平面FAD与平面ADC的夹角的余弦值.
5.()如图,一个正三角形ABC'和一个平行四边形ABDE在同一个平面内,其中AB=8,BD=AD=,AB,DE的中点分别为F,G.现沿直线AB将△ABC'翻折成△ABC,使二面角C-AB-D为120°,设CE的中点为H.
(1)求证:平面CDF∥平面AGH;
(2)求异面直线AB与CE所成角的正切值;
(3)求平面CDE与平面DEF的夹角的余弦值.
6.(2020重庆西南大学附中高二上期末,)如图,四棱锥P-ABCD中,底面ABCD为矩形,侧面PAD为正三角形,AD=2,AB=3,平面PAD⊥平面ABCD,E为棱PB上一点(不与P、B重合),平面ADE交棱PC于点F.
(1)求证:AD∥EF;
(2)若平面BAC与平面ACE夹角的余弦值为,求点B到平面AEC的距离.
7.()如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点.
(1)求异面直线AC与PB间的距离;
(2)在侧面PAB内找一点N,使NE⊥平面PAC,并求出N到AB和AP的距离.
8.(2020河南河大附中高二上期末,)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求平面DAE与平面AEC夹角的余弦值.深度解析
答案全解全析
解答题
1.解析 (1)证明:因为四边形ABCD是菱形,
所以AC⊥BD.
因为PA⊥平面ABCD,BD 平面ABCD,
所以PA⊥BD.
又因为AC∩PA=A,所以BD⊥平面PAC.
(2)设AC∩BD=O.
因为∠BAD=60°,AB=2,
所以BO=1,AO=CO=.
如图,以O为坐标原点,直线OB,OC分别为x轴,y轴,过点O平行于PA的直线为z轴,建立空间直角坐标系Oxyz,
则P(0,-,2),A(0,-,0),B(1,0,0),C(0,,0),
所以=(1,,-2),=(0,2,0).
设PB与AC所成角为θ,
则cos θ===,
即PB与AC所成角的余弦值为.
2.解析 (1)证明:如图,连接EC1、BC1,
因为三棱柱A1B1C1-ABC为直三棱柱,
所以E为AC1的中点.
又因为F为AB的中点,所以EF∥BC1.
又EF 平面BCC1B1,BC1 平面BCC1B1,所以EF∥平面BCC1B1.
(2)以A1为原点,A1C1、A1B1、A1A所在直线分别为x、y、z轴,建立如图所示的空间直角坐标系A1xyz,
则A(0,0,6),B1(0,4,0),E(2,0,3),F(0,2,6),
所以=(0,-2,6),=(2,0,-3),=(0,2,0),
设平面AEF的法向量为n=(x,y,z),则
令x=3,得n=(3,0,2),
记B1F与平面AEF所成角为θ,则sin θ=|cos<,n>|==.
3.解析 建立如图所示的空间直角坐标系,
则A(0,0,0),B(2,2,0),C(0,4,0),C1(0,4,4),∵N是CC1的中点,∴N(0,4,2).
(1)=(0,4,2),=(2,2,0),则||=2,||=4.设点N到直线AB的距离为d1,
则d1===4.
(2)设平面ABN的法向量为n=(x,y,z),则由n⊥,n⊥,
得令z=2,则y=-1,x=,即n=.
易知=(0,0,-2),设点C1到平面ABN的距离为d2,
则d2===.
4.解析 (1)证明:在△ABC中,BC=2,AC=2,∠ACB=45°,
由余弦定理可得AB2=BC2+AC2-2×BC×AC×cos 45°=4,所以AB=2(负值舍去),
因为AC2=AB2+BC2,
所以△ABC是直角三角形,AB⊥BC.
又BE⊥BC,AB∩BE=B,
所以BC⊥平面ABE.
因为AE 平面ABE,所以BC⊥AE,
因为EA⊥AC,AC∩BC=C,
所以AE⊥平面ABCD.
(2)由题易得EB=2AB=4,由(1)知,BC⊥平面ABE,所以平面BEC⊥平面ABE,如图,以B为原点,过点B且垂直于平面BEC的直线为z轴,BE,BC所在直线分别为x,y轴,建立空间直角坐标系Bxyz,则C(0,2,0),E(4,0,0),A(1,0,),D(1,1,),
因为EF=2FC,所以F,
易知=(0,1,0),=,
设平面FAD的法向量为n=(x,y,z),
则
即
令z=,则x=9,所以n=(9,0,).
由(1)知EA⊥平面ABCD,所以=(-3,0,)为平面ABCD的一个法向量.
设平面FAD与平面ADC的夹角为α,
则cos α===,
所以平面FAD与平面ADC的夹角的余弦值为.
5.解析 (1)证明:因为四边形ABDE为平行四边形,F、G分别为AB、DE的中点,
所以四边形FDGA为平行四边形,
所以FD∥AG.
又H、G分别为CE、DE的中点,
所以HG∥CD.
因为FD、CD 平面AGH,AG、HG 平面AGH,所以FD∥平面AGH,CD∥平面AGH,因为FD、CD 平面CDF,FD∩CD=D,所以平面CDF∥平面AGH.
(2)因为三角形ABC为正三角形,BD=AD,F为AB的中点,所以AB⊥CF,AB⊥DF,所以∠CFD为二面角C-AB-D的平面角,又CF∩DF=F,所以AB⊥平面CFD,因为AB 平面ABDE,所以平面CFD⊥平面ABDE.
作CO⊥平面ABDE于O,则O在直线DF上.又二面角C-AB-D的平面角为∠CFD=120°,所以O在线段DF的延长线上.易知CF=4,则FO=2,CO=6.
以F为原点,FD、FA所在直线分别为x轴、y轴,过点F平行于OC的直线为z轴,建立空间直角坐标系,如图,
则A(0,4,0),B(0,-4,0),D(3,0,0),E(3,8,0),C(-2,0,6),
所以=(0,-8,0),=(5,8,-6).
所以异面直线AB与CE所成角的余弦值为|cos<,>|===,
从而其正切值为=.
(3)由(2)知=(5,0,-6),=(0,8,0),设平面CDE的法向量为n1=(x,y,z),则由n1⊥,n1⊥得
令z=5,得n1=(6,0,5).
易知平面DEF的一个法向量n2=(0,0,1),所以平面CDE与平面DEF的夹角的余弦值为|cos
6.解析 (1)证明:∵底面ABCD为矩形,
∴AD∥BC,
又∵AD 平面PBC,BC 平面PBC,
∴AD∥平面PBC.
又∵AD 平面ADE,平面ADE∩平面PBC=EF,∴AD∥EF.
(2)如图,取AD的中点O,连接PO,过点O作OH∥AB交BC于点H.
∵侧面PAD为正三角形,∴PO⊥AD,
∵平面PAD⊥平面ABCD,且交线为AD,
∴PO⊥平面ABCD,∵底面ABCD为矩形,∴AB⊥AD,∴OH⊥AD.
以O为原点,OA,OH,OP所在直线分别为x轴,y轴,z轴建立空间直角坐标系Oxyz,
则O(0,0,0),P(0,0,),A(1,0,0),B(1,3,0),C(-1,3,0),∴=(1,3,-),=(-2,3,0).
设=λ(0<λ<1),
则E(λ,3λ,-λ),
∴=(λ-1,3λ,-λ).
设平面AEC的法向量为n=(x1,y1,z1),
则
令x1=3,则y1=2,z1=.
∴平面AEC的一个法向量为n=.
易知=(0,0,)是平面ABC的一个法向量.
∴|cos<,n>|=
==,
解得λ=,∴E,
∴=.
又∵平面AEC的一个法向量n=(3,2,-3 ),
∴点B到平面AEC的距离为==.
7.解析 (1)由题意得AB⊥AD,PA⊥AD,PA⊥AB.
以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,建立空间直角坐标系,如图,
则A(0,0,0),C(,1,0),P(0,0,2),B(,0,0),
∴=(,1,0),=(,0,-2),=(0,0,2),
设异面直线AC、PB的公垂线的方向向量为n=(x,y,z),则n⊥,n⊥,
∴令x=1,则y=-,z=,即n=.
设异面直线AC、PB之间的距离为d,
则d===.
(2)设在侧面PAB内存在一点N(a,0,c),使NE⊥平面PAC,
由(1)知E,
∴=,
∴
解得∴N,
∴N到AB的距离为1,N 到AP的距离为.
8.解析 (1)证明:由题意可得,△ABD≌△CBD,从而AD=DC.
又△ACD是直角三角形,所以∠ADC=90°.
如图,取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO.
又△ABC是正三角形,所以BO⊥AC.
所以∠DOB为二面角D-AC-B的平面角.
在Rt△AOB中,BO2+AO2=AB2.
又AB=BD,所以BO2+DO2=BO2+AO2=AB2=BD2,
故∠DOB=90°.
所以平面ACD⊥平面ABC.
(2)由题设及(1)知,OA,OB,OD两两垂直,以O为坐标原点,,,的方向分别为x轴,y轴,z轴正方向,||为单位长,建立如图所示的空间直角坐标系Oxyz,则A(1,0,0),B(0,,0),C(-1,0,0),D(0,0,1).
由题设知,四面体ABCE的体积为四面体ABCD的体积的,从而E到平面ABC的距离为D到平面ABC的距离的,即E为DB的中点,得E.
故=(-1,0,1),=(-2,0,0),=.
设n=(x,y,z)是平面DAE的法向量,则即
可取n=.
设m是平面AEC的法向量,则同理可取m=(0,-1,),
则|cos
所以平面DAE与平面AEC夹角的余弦值为.
解题反思 (1)求解本题要注意两点:一是两平面的法向量的夹角不一定是所求的两个平面的夹角;二是利用方程思想进行向量运算时,要认真细心,准确计算.(2)设m,n分别为平面α,β的法向量,则两个平面的夹角θ与
cos θ=|cos
