实数导学案
图片预览



文档简介
13.1 .1 平方根(1)
一、学习目标
1.理解算术平方根的意义,会用根号表示正数的算术平方根,会求一个非负数的算术平方根,掌握算术平方根的非负性。
2.培养逆向思维能力。
二、问题导学(教材P68-72)
●温故知新
1.计算: , , ,
, , 。
2.填一填:,,,
3.若是有理数,则一定是 数。
●投石问路
1.学校要举行美术作品比赛,小鸥很高兴。他想裁出一块面积为25的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
2.什么是算术平方根?任何一个数都有算术平方根吗?若不是,那哪些数有,哪些数没有呢?
●问题摘要:
三、问题探究
●问题指导
(一)算术平方根的定义
1. 填表:
正方形面积
1
9
16
36
边长
表中的问题,实际上是已知一个正数的 ,求 的问题。
2. 算术平方根的定义
一般的,如果一个正数的 等于,即,那么这个正数叫做 算术平方根。
的算术平方根记为 ,读作“ ”, 叫做 。
规定:0的算术平方根是 .
3.小试牛刀:
(1)25的算术平方根是 ;
的算术平方根是 ;
的算术平方根是1;
的算术平方根是0;
(2) 3的算术平方根是 ;
的算术平方根是 ;
表示 ,= ;
= ; 。 (二)算术平方根的性质
1.填一填:
; ;
= ; 。
2.想一想: (≥0);
0
归纳:一个非负数的算术平方根一定是 ,一个非负数的算术平方根的平方一定等于 。要有意义,的取值范围是 。
(三)夹值法求算术平方根的近似值
1.讨论: 的近似值是多少?(精确到0.1)
2.估计的值( )
A.在3到4之间 B.在4到5之间
C.在5到6之间 D.在6到7之间
●问题检测
1. 4的算术平方根是( )
A. 2 B. -2
C. D. 16
2.下列计算正确的是( )
A. B.
C. D.
●问题梳理
●问题拓展
怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?
拼成的大正方形的边长是 。
四、问题达标(用时 分钟,得分: )
1.49的算术平方根是( )
A.7 B.-7 C. D.
2.下列说法正确的是( )
A.
B.
C.
D.
3.要使( )
A. >0 B. ≥0 C. >-4 D. ≥-4
4.估算的值( )
A.在1和2之间 B.在2和3之间
C.在3和4之间 D.在4和5之间
5. ;的算术平方根是 。
6. 若,则= 。
选作:已知的值。
五、学习反思
1.本节有哪些收获?(知识上,思想方法上)
2.课前的疑难解决了吗?有没有新的问题?
13.1 .2 平方根(2)
一、学习目标
1.理解平方根的意义,会用根号表示正数的平方根,会求一个非负数的平方根,掌握平方根的性质。
2.会利用平方根的概念解方程。
二、问题导学(教材P72-75)
●温故知新
1. ,
,。
2. 若,则 。
若,则 。
若,则 。
3.4的算术平方根是 ;
4的平方根是 。
●投石问路
1. 什么是平方根?任何一个数都有平方根吗?若不是,那哪些数有,哪些数没有呢?
2.什么叫开平方?开平方与平方运算有何关系?
3. 平方根与算术平方根有何区别和联系?
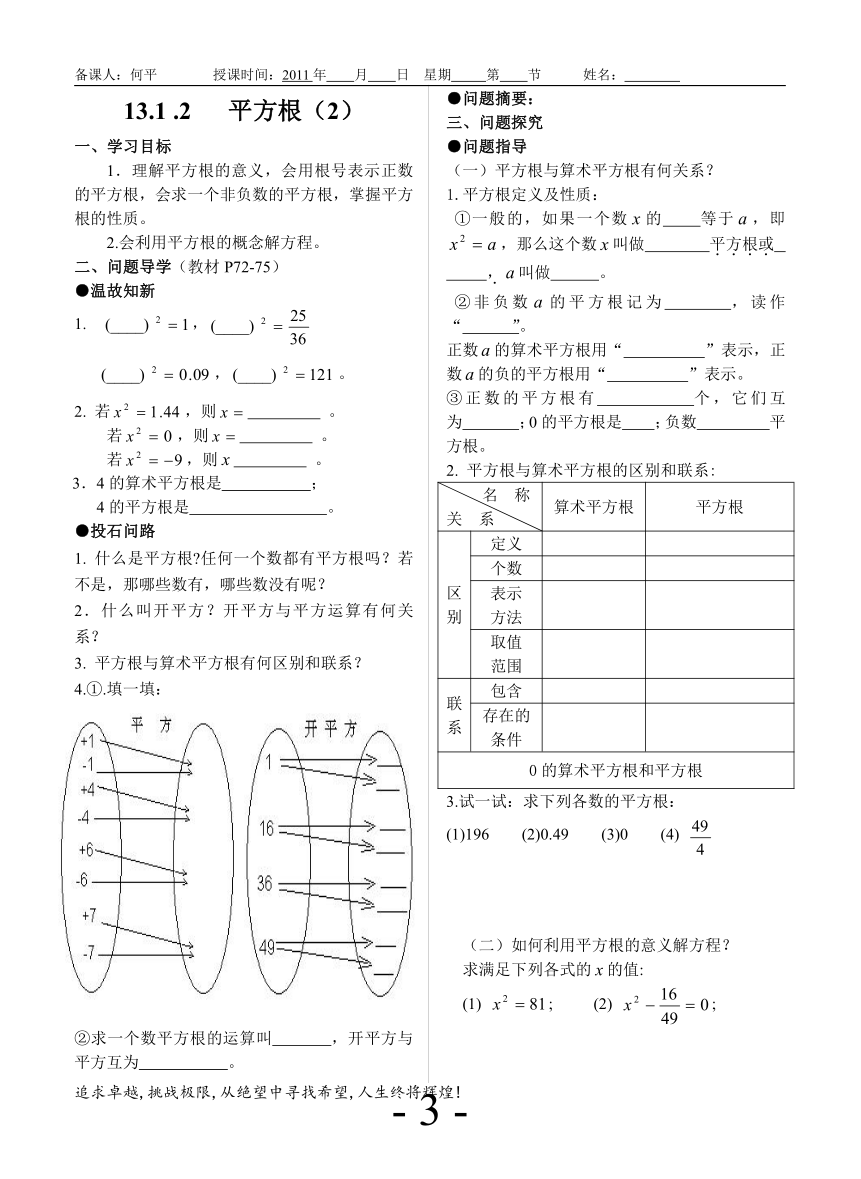
4.①.填一填:
②求一个数平方根的运算叫 ,开平方与平方互为 。
●问题摘要:
三、问题探究
●问题指导
(一)平方根与算术平方根有何关系?
1.平方根定义及性质:
①一般的,如果一个数的 等于,即,那么这个数叫做 平方根或
,叫做 。
②非负数的平方根记为 ,读作“ ”。
正数的算术平方根用“ ”表示,正数的负的平方根用“ ”表示。
③正数的平方根有 个,它们互为 ;0的平方根是 ;负数 平方根。
2. 平方根与算术平方根的区别和联系:
名 称
关 系
算术平方根
平方根
区别
定义
个数
表示
方法
取值
范围
联系
包含
存在的条件
0的算术平方根和平方根
3.试一试:求下列各数的平方根:
(1)196 (2)0.49 (3)0 (4)
(二)如何利用平方根的意义解方程?
求满足下列各式的的值:
(1) ; (2) ;
(3) ; (4)
归纳:①求立方根的运算,需转化为②常常将中看作一个整体。
●问题检测
1.仔细的选一选
(1)9的平方根是( )
A.3 B.-3 C.±3 D. ±
(2)下列说法中不正确的是( )
A.- 是5的平方根
B. 是5的平方根
C.5的平方根是
D.5的算术平方根是
3.求下列各式的值
(1); (2)-;(3)±.
●问题梳理
●问题拓展
如何化简?
1.填一填: , ,
= ,= ,
= …
想想看:=?
2. 试一试:
,,
四、问题达标(用时 分钟,得分: )
1. 的平方根是( )
A.4 B. ±4 C. 2 D .±2
2.下列说法不正确的是( )
A. 是3的算术平方根
B. 的平方根是±4
C.-9的平方根是±3
D.0的平方根和算术平方根都是0.
3.在下列式子中,正确的是( )
A. B.
C. D.
4. 求满足下列各式的的值:
(1) (2)
5.. ,小数部分是 。
6.已知、满足则的平方根是 。
五、学习反思
1.本节有哪些收获?(知识上,思想方法上)
2.课前的疑难解决了吗?有没有新的问题?
13.2 立方根
一、学习目标
1.了解立方根的概念,能用根号表示一个数的立方根。
2.能用类比平方根的方法学习立方根及开立方运算,并区立方根与平方根的不同。了解开立方与立方的关系。
3.能用有理数估计一个无理数的大致范围,培养估算的能力。会利用立方根的概念解方程
二、问题导学(教材P77-79)
●温故知新
1.计算: , , ,
, , , 。
2.填一填:,,,
●投石问路
1.要制作一种容积为27的正方体形状的包装箱,这种包装箱的边长应该是多少?
解:设这种包装箱的边长是,则有
=27
想一想:这个问题,其实就是已知一个数的立方,反过来求这个数。即已知
2.什么叫立方根?什么叫开立方?
①一般的,如果一个数的 等于,即,那么这个数叫做 立方根或
,叫做 。
求一个数的 的运算,叫做 .立方与 互为逆运算。
②填一填:
∵,∴125的立方根是 ;
∵,∴0的立方根是 ;
∵,∴-8的立方根是 ;
∵,∴的立方根是 ;
③.正数的立方根是 数; 0的立方根是 ;负数的立方根是 数。
●问题摘要:
三、问题探究
●问题指导
(一)立方根如何表示?
①一个数的立方根记为 ,读作“ ”。
②读作 ,叫 ,3叫 。
④表示 ,= ,
-27的立方根是 ,-3的立方根是 。
(二)平方根与立方根性质有何区别?
数项 目
正数
0
负数
平方根
立方根
(三)有何性质?
1.(1)∵
∴;
(2)∵
∴。
…
2.一般地,,
,。
(四)如何立方根的意义解方程?
求满足下列各式的的值:
(1) ; (2) ;
(3) ; (4)
归纳:①求立方根的运算,需转化为②常常将中看作一个整体。
●问题检测
1. -0.027的立方根是( )
A.0.3 B.±0.03 C.-0.3 D.0.003
2.若一个数的平方根是±8,则这个数的立方根是( )
A.4 B. ±4 C.2 D.±2
3. 求下列格式的值
(1) (2) (3) (4)
●问题梳理
●问题拓展
已知的算术平方根,的立方根,试求的值。
四、问题达标(用时 分钟,得分: )
1.下列说法正确的是( )
A. 的立方根是±
B. 的立方根是
C. -8没有立方根
D.-7的立方根是
2.如果,那么=( )
A.±1 B.1 C.-1 D.以上答案都不对
3.下列四个说法:①1的是算术平方根是1;②的立方根是±;③立方根等于本身的数只有0;④互为相反数的两个数的立方根互为相反数,其中正确的是( )
A. ①② B. ①③ C. ①④ D. ②④
4.估计39的立方根的大小在( )
A.2与3之间 B.3与4之间
C.4与5之间 D.5与6之间
5.下列计算错误的是( )
A. B.
C. D.
6. ,,
-8的立方根与81的平方根之和为 .
7.求满足下列各式的的值:
选作:已知,则求算术平方根是 。
五、学习反思
1.本节有哪些收获?(知识上,思想方法上)
2.课前的疑难解决了吗?有没有新的问题?
13.3.1 实数(1)
一、学习目标
1.了解无理数和实数的概念,能按要求对实数进行分类。
2.了解数轴上的点与实数一一对应,能用数轴上的点来表示无理数。进一步领会数形结合的思想。
3.会求实数的相反数和绝对值。
二、问题导学(教材P82-84)
●温故知新
把下列有理数写成小数的形式,你能发现什么?
3, , , , , 。
①任何一个有理数都可以写成 小数或 小数的形式。②反过来,任何 小数或 小数都是有理数。
2.回顾有理数分类,画出有理数的分类图。
什么叫数轴?把下列各数在数轴上表示出来
1.5 -3
●投石问路
1.什么叫无理数?
在前面我们学习了求一个数的平方根和立方根时,有些数的平方根或立方根是无限不循环小数,。。如:…都是无理数,π=3.14159265…也是无理数。我们把无限不循环小数叫做无理数。
小结:我们目前学习的无理数有下面三种形式
开方开不尽的数,如:,,,…②圆周率π,它是无限不循环小数
③类似0.1010010001…(每两个1之间依次多1个1)
2. 用根号表示的数一定是无理数吗?举例说明
3. 尝试画出无理数分类图。
●问题摘要:
三、问题探究
●问题指导
(一)什么叫实数?如何分类?
1.实数的定义: 和 统称实数。
2.实数的分类
(1)按定义分:
(2)按性质分:
试一试:
下列各数哪些是有理数?哪些是无理数?
3.1 .02020020002…,,-π,,,,。
(二):数轴上的点与什么数成一一对应?
我们知道有理数都可以在数轴上表示出来,但是数轴上的点是不是都表示有理数?无理数在数轴上有点吗?
实验:1.将一个直径为1个单位的圆在数轴上滚动一周,圆上的点由原点到达O',点O'的对应点是
思考:上面的实验说明了: 。
2.以一个单位长度为边画一个正方形,以原点为圆心,正方形的对角线为半径画弧,弧与数轴的交点表示: 、 。
上面的实验说明: 数可以用数轴上的点表示出来。也就是说数轴上的点有的表示: 、有的表示: 。
归纳:数轴上的点与 数成一 一对应。
(三)怎样求实数的相反数和绝对值?
在数轴上一个实数的绝对值是表示这个数的点到 的距离:两个互为相反数的实数就是表示这两个数的点一个在 ,一个在 ,它们到原点的距离 。
试试看:(1)相反数:π的相反数是 ,
的相反数是 ,0的相反数是 。..
小结:实数的相反数是 。
(2)绝对值:= ,= ,
= ,= ,
小结:一个正实数的绝对值 ,一个负实数的绝对值是 ,0的绝对值是 。
●问题检测
1.下列各数,一定是无理数的是( )
A.带根号的数 B.无限小数
C.不循环小数 D.无限不循环小数
2.在实数5、、、中,无理数是( )
A.5 B. C. D.
3. 的相反数是 ,绝对值是的数是 。
●问题梳理
●问题拓展
的相反数 ,的相反数 ;
四、问题达标(用时 分钟,得分: )
1.和数轴上的点一一对应的是( )
A.整数 B.有理数 C.无理数 D.实数
2.在实数π,,,,0.2121121112…(每两个2之间依次多1个1),中,无理数共有( )
A.2个 B.3个 C.4个 D.5个
3.有一个数值转换器,原理如图,当输入的为64时,输出的是( )
A.8 B. C.4 D.2
4.已知实数和互为相反数,实数和互为倒数,的倒数等于它本身,则- = 。
五、学习反思
1.本节有哪些收获?(知识上,思想方法上)
2.课前的疑难解决了吗?有没有新的问题?
13.3.2 实数(2)
一、学习目标
1.学会比较两个实数的大小,能熟练地进行实数运算。
2. 进一步领会数形结合的思想。
二、问题导学(教材P85-86)
●温故知新
1.在数轴上表示的数,右边的数总比左边的数 。
2.计算:= ,= ,= ,
= ,= ,= 。
3.计算:= 。
4.计算的结果是( )
A.3 B.7 C.-3 D. -7
●投石问路
1.有理数中的运算法则及性质是否在实数范围内也适用呢?
2.实数如何进行的大小比较呢?
比较大小: 2,
= , π
3.= ,= 。
●问题摘要:
三、问题探究
●问题指导
(一)实数的大小比较
下列式中,正确的是( )
A. B.
C. D.
小结:进行实数的大小比较时,应把各数统一转化成一种形式。如:第1题,把10转化成,把11转化成,把12转化成,
把1,32转化成,再比较大小,较简便。
(二)实数的运算
1.计算:
(1) (2)
2.小结:实数运算中,有理数的运算法则及运算性质等同样适用。
3. 计算下列各式的值:
(1)
(2)
(三)实数运算求近似值
计算(结果保留小数点后两位)
(1) (2)
●问题检测
1. P87第6题
2.( )
A.互为相反数 B.互为倒数
C.相等 D.以上都不对
3.化简:
(1)= ;
(2)= 。
4.若。
5. ,5.-3,,的大小顺序是( )
A. <-3<<
B. <-3<<
C. -3<<<
D. -3<<<
6.计算与化简:
7. P86练习第3题
●问题梳理
●问题拓展
1.化简:
2.
四、问题达标(用时 分钟,得分: )
1. 等于( )
A. B.3 C. D.1
2. 等于( )
A. B.2 C.1 D.0
3.下列四个数中与最接近的数是( )
A.2 B.3 C.4 D.5
4.在下列各式中,正确的是( )
A. B.
C. D.
5.计算下列各式
(1)
(2)
6.如图所示,在平行四边形ABCO中,已知A、C两点的坐标为A(,),C(2,0).
(1)求点B的得坐标;
(2)求平行四边形ABCO向左平移个单位长度后所得四边形的A′B′C′D′四个顶点的坐标;
(3)求平行四边形ABCO的面积。
五、学习反思
1.本节有哪些收获?(知识上,思想方法上)
2.课前的疑难解决了吗?有没有新的问题?
第13章 “实数”复习案
一、学习目标
1.了解平方根、算术平方根、立方根的概念,会用根号表示数的平方根、立方根。
2.了解开方与乘方互为逆运算,会用平方根运算求某些非负数的平方根,会用立方根运算求某些数的立方根。
3.了解无理数和实数的概念,知道实数与数轴上的点一 一对应,会比较实数的大小。
4.能用有理数估计一个无理数的大致范围。
5.掌握数形结合、转化、方程、整体思想在解题中的应用。
二、问题导学
●体系构建(教材P90)
三、.考点归类整理与练习
考点一:平方根与算术平方根
1.非负数的平方根表示为 ,算术平方根表示为 ,即就是平方根中 。
2.一个正数的平方根有 个,它们互为 ;0的平方根和算术平方根都是 ;负数 。
3.算术平方根具有 性。
4. 9的算术平方根是( )
A.±3 B.-3 C. 3 D.
5.121的平方根是±11的数学表达式是( )
A. B.
C. D.
6.下列式子中,正确的是( )
A. B.
C. D.
7.估算的值在( )
A.2和3之间 B. 3和4之间
C. 4和5之间 D. 5和6之间
8.已知,是实数,,则= 。
9.如果2-18=0,则的平方根是 。
10.若有意义,则= 。
考点二:立方根
1.数的立方根表示为 。一个正数的立方根是 ,负数的立方根是 ;0的立方根是 ;立方根等于本身的数有 。
2. ,
,
3.下列说法正确的是( )
A.一个数的立方根有两个,它们互为相反数;
B.负数没有立方根;
C.如果一个数有平方根,那么它一定有立方根;
D.一个数的立方根与被开方数同号。
4.一个数的平方根等于它本身,则这个数的立方根是( )
A.1 B.0 C.-1 D.1、-1或0
5.若式子有意义,则的取值范围是( )
A. ≥2 B.≤3 C.2≤≤3 D.以上都不对。
6.计算:= ,= ,
7. 的平方根是 ,-的立方根是 。
8.-27的立方根与的平方根的和是 。
考点三:实数及大小比较
1. 和 统称实数。
2.有限小数和无限 小数叫有理数,无限 无理数。
3.在实数,0,,π,-3.14, 中,无理数有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法正确的有( )
①无限小数一定是无理数;②带根号的数都是无理数;③实数可以分为正实数和负实数;④有理数和无理数统称实数。
A.1个 B.2个 C.3个 D.4个
5.已知为实数,则等于( )
A. B.- C. -1 D.0
6. 的相反数是 ,绝对值是 .,
7.比较大小:- -,
8.把下列各数填入相应的集合里:,21.3,,,0,,,1.3131131113…
(1)无理数集合:{ … }
(2)负分数集合:{ … }
(3)整数集合:{ … }
9. 已知 ,,则- ,- ,已知,且,则x≈ .
10.一个正数b的平方根分别是和,则a= ,b
考点四:实数的运算
.1.计算与化简
(1)
(2)
(3)
2.求满足下列各式的的值:
(1) (2)
3.如果是的整数部分,是的小数部分,求的值
6.如图所示,在平行四边形ABCD中,已知A、B、C三点的坐标为A(,),B(1,0),C(,0).
(1)求点D的坐标;
(2)将平行四边形ABCD向下平移个单位长度,求后所得四边形的四个顶点的坐标;
(3)求平行四边形ABCD的面积。
第13章 实数检测试题
(45分钟完卷)
班级: 姓名: 得分:
一、选择题(每小题4分,共20分)
1. 25的算术平方根是( )
A、5 B、–5 C、 D、
2.下列等式中,错误的是( )
A、 B、
C、 D、
3.在实数-7,0.9,,-,,中,无理数有( )
A、1个 B、2个 C、3个 D、4个
4.若,则估计的值所在的范围是( )
A、1<<2 B、2<<3
C、3<<4 D、4<<5
5.如图所示,下列存在算术平方根的是( )
A、 B、
C、 D、
二、填空题(每小题4分,共20分)
6.若,则= 。
7.若,则的立方根是 。
8.比较大小:5 ,
9.绝对值是的数是 ;的相反数是 。
10.若一个正数的平方根是和,则这个正数是
三、解答题:(共60分)
1.计算:(每小题7分,共21分)
(1)
(2)
(3)
2.求满足下列各式的的值: (每小题7分,共14分)
(1)
(2)
3.(1)若,其中a=6,b=8,求的值。(6分)
(2)若,其中=25,b=15,求a的值。(6分)
4.如图,坐标轴上点A,C的坐标分别为,0),(0,1),点A关于轴的对称点为B,设点B的坐标为,0)。(12分)
(1)求得值;
(2)试判断△ABC的形状,并求出△ABC得面积。
选作题:
1.数轴上的点A表示,点A 和数轴上的点B相距2个单位长度,则点B所表示的实数是 。
2.已知的整数部分为a,小数部分为b,则(1)a+b= (2)a-b=
3. 设、为实数,且,则=
一、学习目标
1.理解算术平方根的意义,会用根号表示正数的算术平方根,会求一个非负数的算术平方根,掌握算术平方根的非负性。
2.培养逆向思维能力。
二、问题导学(教材P68-72)
●温故知新
1.计算: , , ,
, , 。
2.填一填:,,,
3.若是有理数,则一定是 数。
●投石问路
1.学校要举行美术作品比赛,小鸥很高兴。他想裁出一块面积为25的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
2.什么是算术平方根?任何一个数都有算术平方根吗?若不是,那哪些数有,哪些数没有呢?
●问题摘要:
三、问题探究
●问题指导
(一)算术平方根的定义
1. 填表:
正方形面积
1
9
16
36
边长
表中的问题,实际上是已知一个正数的 ,求 的问题。
2. 算术平方根的定义
一般的,如果一个正数的 等于,即,那么这个正数叫做 算术平方根。
的算术平方根记为 ,读作“ ”, 叫做 。
规定:0的算术平方根是 .
3.小试牛刀:
(1)25的算术平方根是 ;
的算术平方根是 ;
的算术平方根是1;
的算术平方根是0;
(2) 3的算术平方根是 ;
的算术平方根是 ;
表示 ,= ;
= ; 。 (二)算术平方根的性质
1.填一填:
; ;
= ; 。
2.想一想: (≥0);
0
归纳:一个非负数的算术平方根一定是 ,一个非负数的算术平方根的平方一定等于 。要有意义,的取值范围是 。
(三)夹值法求算术平方根的近似值
1.讨论: 的近似值是多少?(精确到0.1)
2.估计的值( )
A.在3到4之间 B.在4到5之间
C.在5到6之间 D.在6到7之间
●问题检测
1. 4的算术平方根是( )
A. 2 B. -2
C. D. 16
2.下列计算正确的是( )
A. B.
C. D.
●问题梳理
●问题拓展
怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?
拼成的大正方形的边长是 。
四、问题达标(用时 分钟,得分: )
1.49的算术平方根是( )
A.7 B.-7 C. D.
2.下列说法正确的是( )
A.
B.
C.
D.
3.要使( )
A. >0 B. ≥0 C. >-4 D. ≥-4
4.估算的值( )
A.在1和2之间 B.在2和3之间
C.在3和4之间 D.在4和5之间
5. ;的算术平方根是 。
6. 若,则= 。
选作:已知的值。
五、学习反思
1.本节有哪些收获?(知识上,思想方法上)
2.课前的疑难解决了吗?有没有新的问题?
13.1 .2 平方根(2)
一、学习目标
1.理解平方根的意义,会用根号表示正数的平方根,会求一个非负数的平方根,掌握平方根的性质。
2.会利用平方根的概念解方程。
二、问题导学(教材P72-75)
●温故知新
1. ,
,。
2. 若,则 。
若,则 。
若,则 。
3.4的算术平方根是 ;
4的平方根是 。
●投石问路
1. 什么是平方根?任何一个数都有平方根吗?若不是,那哪些数有,哪些数没有呢?
2.什么叫开平方?开平方与平方运算有何关系?
3. 平方根与算术平方根有何区别和联系?
4.①.填一填:
②求一个数平方根的运算叫 ,开平方与平方互为 。
●问题摘要:
三、问题探究
●问题指导
(一)平方根与算术平方根有何关系?
1.平方根定义及性质:
①一般的,如果一个数的 等于,即,那么这个数叫做 平方根或
,叫做 。
②非负数的平方根记为 ,读作“ ”。
正数的算术平方根用“ ”表示,正数的负的平方根用“ ”表示。
③正数的平方根有 个,它们互为 ;0的平方根是 ;负数 平方根。
2. 平方根与算术平方根的区别和联系:
名 称
关 系
算术平方根
平方根
区别
定义
个数
表示
方法
取值
范围
联系
包含
存在的条件
0的算术平方根和平方根
3.试一试:求下列各数的平方根:
(1)196 (2)0.49 (3)0 (4)
(二)如何利用平方根的意义解方程?
求满足下列各式的的值:
(1) ; (2) ;
(3) ; (4)
归纳:①求立方根的运算,需转化为②常常将中看作一个整体。
●问题检测
1.仔细的选一选
(1)9的平方根是( )
A.3 B.-3 C.±3 D. ±
(2)下列说法中不正确的是( )
A.- 是5的平方根
B. 是5的平方根
C.5的平方根是
D.5的算术平方根是
3.求下列各式的值
(1); (2)-;(3)±.
●问题梳理
●问题拓展
如何化简?
1.填一填: , ,
= ,= ,
= …
想想看:=?
2. 试一试:
,,
四、问题达标(用时 分钟,得分: )
1. 的平方根是( )
A.4 B. ±4 C. 2 D .±2
2.下列说法不正确的是( )
A. 是3的算术平方根
B. 的平方根是±4
C.-9的平方根是±3
D.0的平方根和算术平方根都是0.
3.在下列式子中,正确的是( )
A. B.
C. D.
4. 求满足下列各式的的值:
(1) (2)
5.. ,小数部分是 。
6.已知、满足则的平方根是 。
五、学习反思
1.本节有哪些收获?(知识上,思想方法上)
2.课前的疑难解决了吗?有没有新的问题?
13.2 立方根
一、学习目标
1.了解立方根的概念,能用根号表示一个数的立方根。
2.能用类比平方根的方法学习立方根及开立方运算,并区立方根与平方根的不同。了解开立方与立方的关系。
3.能用有理数估计一个无理数的大致范围,培养估算的能力。会利用立方根的概念解方程
二、问题导学(教材P77-79)
●温故知新
1.计算: , , ,
, , , 。
2.填一填:,,,
●投石问路
1.要制作一种容积为27的正方体形状的包装箱,这种包装箱的边长应该是多少?
解:设这种包装箱的边长是,则有
=27
想一想:这个问题,其实就是已知一个数的立方,反过来求这个数。即已知
2.什么叫立方根?什么叫开立方?
①一般的,如果一个数的 等于,即,那么这个数叫做 立方根或
,叫做 。
求一个数的 的运算,叫做 .立方与 互为逆运算。
②填一填:
∵,∴125的立方根是 ;
∵,∴0的立方根是 ;
∵,∴-8的立方根是 ;
∵,∴的立方根是 ;
③.正数的立方根是 数; 0的立方根是 ;负数的立方根是 数。
●问题摘要:
三、问题探究
●问题指导
(一)立方根如何表示?
①一个数的立方根记为 ,读作“ ”。
②读作 ,叫 ,3叫 。
④表示 ,= ,
-27的立方根是 ,-3的立方根是 。
(二)平方根与立方根性质有何区别?
数项 目
正数
0
负数
平方根
立方根
(三)有何性质?
1.(1)∵
∴;
(2)∵
∴。
…
2.一般地,,
,。
(四)如何立方根的意义解方程?
求满足下列各式的的值:
(1) ; (2) ;
(3) ; (4)
归纳:①求立方根的运算,需转化为②常常将中看作一个整体。
●问题检测
1. -0.027的立方根是( )
A.0.3 B.±0.03 C.-0.3 D.0.003
2.若一个数的平方根是±8,则这个数的立方根是( )
A.4 B. ±4 C.2 D.±2
3. 求下列格式的值
(1) (2) (3) (4)
●问题梳理
●问题拓展
已知的算术平方根,的立方根,试求的值。
四、问题达标(用时 分钟,得分: )
1.下列说法正确的是( )
A. 的立方根是±
B. 的立方根是
C. -8没有立方根
D.-7的立方根是
2.如果,那么=( )
A.±1 B.1 C.-1 D.以上答案都不对
3.下列四个说法:①1的是算术平方根是1;②的立方根是±;③立方根等于本身的数只有0;④互为相反数的两个数的立方根互为相反数,其中正确的是( )
A. ①② B. ①③ C. ①④ D. ②④
4.估计39的立方根的大小在( )
A.2与3之间 B.3与4之间
C.4与5之间 D.5与6之间
5.下列计算错误的是( )
A. B.
C. D.
6. ,,
-8的立方根与81的平方根之和为 .
7.求满足下列各式的的值:
选作:已知,则求算术平方根是 。
五、学习反思
1.本节有哪些收获?(知识上,思想方法上)
2.课前的疑难解决了吗?有没有新的问题?
13.3.1 实数(1)
一、学习目标
1.了解无理数和实数的概念,能按要求对实数进行分类。
2.了解数轴上的点与实数一一对应,能用数轴上的点来表示无理数。进一步领会数形结合的思想。
3.会求实数的相反数和绝对值。
二、问题导学(教材P82-84)
●温故知新
把下列有理数写成小数的形式,你能发现什么?
3, , , , , 。
①任何一个有理数都可以写成 小数或 小数的形式。②反过来,任何 小数或 小数都是有理数。
2.回顾有理数分类,画出有理数的分类图。
什么叫数轴?把下列各数在数轴上表示出来
1.5 -3
●投石问路
1.什么叫无理数?
在前面我们学习了求一个数的平方根和立方根时,有些数的平方根或立方根是无限不循环小数,。。如:…都是无理数,π=3.14159265…也是无理数。我们把无限不循环小数叫做无理数。
小结:我们目前学习的无理数有下面三种形式
开方开不尽的数,如:,,,…②圆周率π,它是无限不循环小数
③类似0.1010010001…(每两个1之间依次多1个1)
2. 用根号表示的数一定是无理数吗?举例说明
3. 尝试画出无理数分类图。
●问题摘要:
三、问题探究
●问题指导
(一)什么叫实数?如何分类?
1.实数的定义: 和 统称实数。
2.实数的分类
(1)按定义分:
(2)按性质分:
试一试:
下列各数哪些是有理数?哪些是无理数?
3.1 .02020020002…,,-π,,,,。
(二):数轴上的点与什么数成一一对应?
我们知道有理数都可以在数轴上表示出来,但是数轴上的点是不是都表示有理数?无理数在数轴上有点吗?
实验:1.将一个直径为1个单位的圆在数轴上滚动一周,圆上的点由原点到达O',点O'的对应点是
思考:上面的实验说明了: 。
2.以一个单位长度为边画一个正方形,以原点为圆心,正方形的对角线为半径画弧,弧与数轴的交点表示: 、 。
上面的实验说明: 数可以用数轴上的点表示出来。也就是说数轴上的点有的表示: 、有的表示: 。
归纳:数轴上的点与 数成一 一对应。
(三)怎样求实数的相反数和绝对值?
在数轴上一个实数的绝对值是表示这个数的点到 的距离:两个互为相反数的实数就是表示这两个数的点一个在 ,一个在 ,它们到原点的距离 。
试试看:(1)相反数:π的相反数是 ,
的相反数是 ,0的相反数是 。..
小结:实数的相反数是 。
(2)绝对值:= ,= ,
= ,= ,
小结:一个正实数的绝对值 ,一个负实数的绝对值是 ,0的绝对值是 。
●问题检测
1.下列各数,一定是无理数的是( )
A.带根号的数 B.无限小数
C.不循环小数 D.无限不循环小数
2.在实数5、、、中,无理数是( )
A.5 B. C. D.
3. 的相反数是 ,绝对值是的数是 。
●问题梳理
●问题拓展
的相反数 ,的相反数 ;
四、问题达标(用时 分钟,得分: )
1.和数轴上的点一一对应的是( )
A.整数 B.有理数 C.无理数 D.实数
2.在实数π,,,,0.2121121112…(每两个2之间依次多1个1),中,无理数共有( )
A.2个 B.3个 C.4个 D.5个
3.有一个数值转换器,原理如图,当输入的为64时,输出的是( )
A.8 B. C.4 D.2
4.已知实数和互为相反数,实数和互为倒数,的倒数等于它本身,则- = 。
五、学习反思
1.本节有哪些收获?(知识上,思想方法上)
2.课前的疑难解决了吗?有没有新的问题?
13.3.2 实数(2)
一、学习目标
1.学会比较两个实数的大小,能熟练地进行实数运算。
2. 进一步领会数形结合的思想。
二、问题导学(教材P85-86)
●温故知新
1.在数轴上表示的数,右边的数总比左边的数 。
2.计算:= ,= ,= ,
= ,= ,= 。
3.计算:= 。
4.计算的结果是( )
A.3 B.7 C.-3 D. -7
●投石问路
1.有理数中的运算法则及性质是否在实数范围内也适用呢?
2.实数如何进行的大小比较呢?
比较大小: 2,
= , π
3.= ,= 。
●问题摘要:
三、问题探究
●问题指导
(一)实数的大小比较
下列式中,正确的是( )
A. B.
C. D.
小结:进行实数的大小比较时,应把各数统一转化成一种形式。如:第1题,把10转化成,把11转化成,把12转化成,
把1,32转化成,再比较大小,较简便。
(二)实数的运算
1.计算:
(1) (2)
2.小结:实数运算中,有理数的运算法则及运算性质等同样适用。
3. 计算下列各式的值:
(1)
(2)
(三)实数运算求近似值
计算(结果保留小数点后两位)
(1) (2)
●问题检测
1. P87第6题
2.( )
A.互为相反数 B.互为倒数
C.相等 D.以上都不对
3.化简:
(1)= ;
(2)= 。
4.若。
5. ,5.-3,,的大小顺序是( )
A. <-3<<
B. <-3<<
C. -3<<<
D. -3<<<
6.计算与化简:
7. P86练习第3题
●问题梳理
●问题拓展
1.化简:
2.
四、问题达标(用时 分钟,得分: )
1. 等于( )
A. B.3 C. D.1
2. 等于( )
A. B.2 C.1 D.0
3.下列四个数中与最接近的数是( )
A.2 B.3 C.4 D.5
4.在下列各式中,正确的是( )
A. B.
C. D.
5.计算下列各式
(1)
(2)
6.如图所示,在平行四边形ABCO中,已知A、C两点的坐标为A(,),C(2,0).
(1)求点B的得坐标;
(2)求平行四边形ABCO向左平移个单位长度后所得四边形的A′B′C′D′四个顶点的坐标;
(3)求平行四边形ABCO的面积。
五、学习反思
1.本节有哪些收获?(知识上,思想方法上)
2.课前的疑难解决了吗?有没有新的问题?
第13章 “实数”复习案
一、学习目标
1.了解平方根、算术平方根、立方根的概念,会用根号表示数的平方根、立方根。
2.了解开方与乘方互为逆运算,会用平方根运算求某些非负数的平方根,会用立方根运算求某些数的立方根。
3.了解无理数和实数的概念,知道实数与数轴上的点一 一对应,会比较实数的大小。
4.能用有理数估计一个无理数的大致范围。
5.掌握数形结合、转化、方程、整体思想在解题中的应用。
二、问题导学
●体系构建(教材P90)
三、.考点归类整理与练习
考点一:平方根与算术平方根
1.非负数的平方根表示为 ,算术平方根表示为 ,即就是平方根中 。
2.一个正数的平方根有 个,它们互为 ;0的平方根和算术平方根都是 ;负数 。
3.算术平方根具有 性。
4. 9的算术平方根是( )
A.±3 B.-3 C. 3 D.
5.121的平方根是±11的数学表达式是( )
A. B.
C. D.
6.下列式子中,正确的是( )
A. B.
C. D.
7.估算的值在( )
A.2和3之间 B. 3和4之间
C. 4和5之间 D. 5和6之间
8.已知,是实数,,则= 。
9.如果2-18=0,则的平方根是 。
10.若有意义,则= 。
考点二:立方根
1.数的立方根表示为 。一个正数的立方根是 ,负数的立方根是 ;0的立方根是 ;立方根等于本身的数有 。
2. ,
,
3.下列说法正确的是( )
A.一个数的立方根有两个,它们互为相反数;
B.负数没有立方根;
C.如果一个数有平方根,那么它一定有立方根;
D.一个数的立方根与被开方数同号。
4.一个数的平方根等于它本身,则这个数的立方根是( )
A.1 B.0 C.-1 D.1、-1或0
5.若式子有意义,则的取值范围是( )
A. ≥2 B.≤3 C.2≤≤3 D.以上都不对。
6.计算:= ,= ,
7. 的平方根是 ,-的立方根是 。
8.-27的立方根与的平方根的和是 。
考点三:实数及大小比较
1. 和 统称实数。
2.有限小数和无限 小数叫有理数,无限 无理数。
3.在实数,0,,π,-3.14, 中,无理数有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法正确的有( )
①无限小数一定是无理数;②带根号的数都是无理数;③实数可以分为正实数和负实数;④有理数和无理数统称实数。
A.1个 B.2个 C.3个 D.4个
5.已知为实数,则等于( )
A. B.- C. -1 D.0
6. 的相反数是 ,绝对值是 .,
7.比较大小:- -,
8.把下列各数填入相应的集合里:,21.3,,,0,,,1.3131131113…
(1)无理数集合:{ … }
(2)负分数集合:{ … }
(3)整数集合:{ … }
9. 已知 ,,则- ,- ,已知,且,则x≈ .
10.一个正数b的平方根分别是和,则a= ,b
考点四:实数的运算
.1.计算与化简
(1)
(2)
(3)
2.求满足下列各式的的值:
(1) (2)
3.如果是的整数部分,是的小数部分,求的值
6.如图所示,在平行四边形ABCD中,已知A、B、C三点的坐标为A(,),B(1,0),C(,0).
(1)求点D的坐标;
(2)将平行四边形ABCD向下平移个单位长度,求后所得四边形的四个顶点的坐标;
(3)求平行四边形ABCD的面积。
第13章 实数检测试题
(45分钟完卷)
班级: 姓名: 得分:
一、选择题(每小题4分,共20分)
1. 25的算术平方根是( )
A、5 B、–5 C、 D、
2.下列等式中,错误的是( )
A、 B、
C、 D、
3.在实数-7,0.9,,-,,中,无理数有( )
A、1个 B、2个 C、3个 D、4个
4.若,则估计的值所在的范围是( )
A、1<<2 B、2<<3
C、3<<4 D、4<<5
5.如图所示,下列存在算术平方根的是( )
A、 B、
C、 D、
二、填空题(每小题4分,共20分)
6.若,则= 。
7.若,则的立方根是 。
8.比较大小:5 ,
9.绝对值是的数是 ;的相反数是 。
10.若一个正数的平方根是和,则这个正数是
三、解答题:(共60分)
1.计算:(每小题7分,共21分)
(1)
(2)
(3)
2.求满足下列各式的的值: (每小题7分,共14分)
(1)
(2)
3.(1)若,其中a=6,b=8,求的值。(6分)
(2)若,其中=25,b=15,求a的值。(6分)
4.如图,坐标轴上点A,C的坐标分别为,0),(0,1),点A关于轴的对称点为B,设点B的坐标为,0)。(12分)
(1)求得值;
(2)试判断△ABC的形状,并求出△ABC得面积。
选作题:
1.数轴上的点A表示,点A 和数轴上的点B相距2个单位长度,则点B所表示的实数是 。
2.已知的整数部分为a,小数部分为b,则(1)a+b= (2)a-b=
3. 设、为实数,且,则=
