苏科版九下数学 6.4探索三角形相似的条件 学案(无答案)
文档属性
| 名称 | 苏科版九下数学 6.4探索三角形相似的条件 学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 204.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 00:00:00 | ||
图片预览

文档简介
探索三角形相似的条件
一、学习内容:中考复习小专题:三角形的中线
二、学习目标:巩固、梳理与中线相关的知识点,认识相关知识点之间的联系,培养学生发散思维和根据题目相关条件进行综合分析、解决问题的能力。
教学重点: 梳理与中线相关的知识点,认识相关知识点之间的联系。
教学难点: 根据题目相关条件进行综合分析、解决问题的能力。
三、课堂前测:
(1) 叫做三角形的中线。
(2)如图1,△ABC中,AB=AC=13,BC=10,BC边上的中线长为 。
(3)如图2,△ABC中,∠C=90°,AC=6,BC=8,AB边上的中线长为 。
图1 图2 图3
(4) 如图3,已知AD为△ABC的中线,且S△ABC=10,则S△ABD= 。
(5) 如图4,△ABC的两条中线BD、CE相交于点G,点G叫做三角形的 ,DG:BG= 。
图4 图5
(6) 如图5,已知△ABC∽△A’B’C’,且相似比为2:3,AD、A’D’分别为△ABC、△A’B’C’的中线,那么AD:A’D’ = 。
四、学习过程:
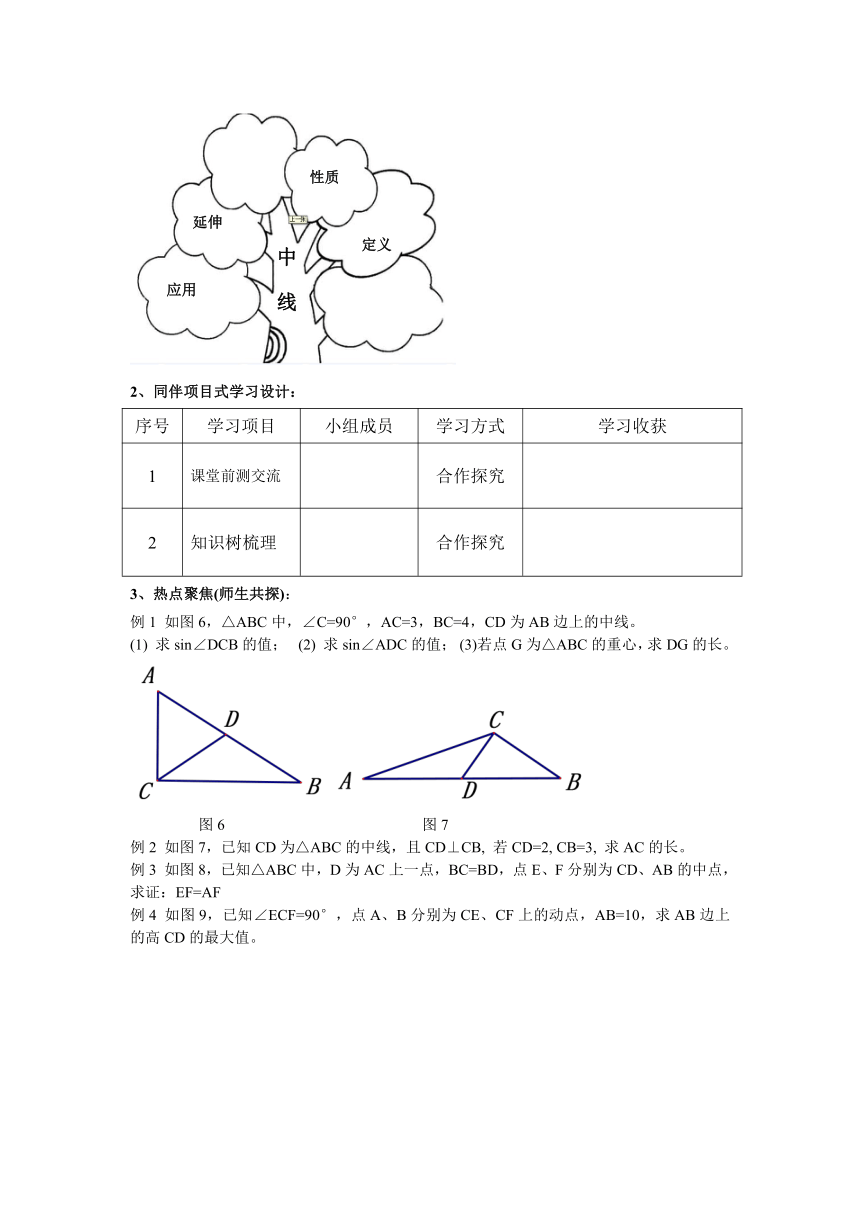
1、知识结构梳理:
2、同伴项目式学习设计:
序号 学习项目 小组成员 学习方式 学习收获
1 课堂前测交流 合作探究
2 知识树梳理 合作探究
3、热点聚焦(师生共探):
例1 如图6,△ABC中,∠C=90°,AC=3,BC=4,CD为AB边上的中线。
(1) 求sin∠DCB的值; (2) 求sin∠ADC的值; (3)若点G为△ABC的重心,求DG的长。
图6 图7
例2 如图7,已知CD为△ABC的中线,且CD⊥CB, 若CD=2, CB=3, 求AC的长。
例3 如图8,已知△ABC中,D为AC上一点,BC=BD,点E、F分别为CD、AB的中点,求证:EF=AF
例4 如图9,已知∠ECF=90°,点A、B分别为CE、CF上的动点,AB=10,求AB边上的高CD的最大值。
图8 图9
五、随堂反馈:
(一)基础知识简单应用层——自主学习我最棒!
1. 如图10,已知点E、F分别为四边形ABCD的边BC、CD的中点,如果四边形ABCD的面积为18,那么四边形AECF的面积是多少?
图10 图11
2. 如图11,四边形ABCD中,∠ABC=∠ADC=90°,点E、F分别为对角线AC、BD的中点,求证:EF⊥BD
(二)具有一定开放性和思辨性的知识应用层——训练反馈显身手!
★3.如图12,已知AD为△ABC的中线,如果AB=3, AC=5, 那么AD的取值范围是多少?
图12 图13
★4.如图13,△ABC中,AB=AC=13,BC=10,点G为△ABC的重心,求BG的长。
(三)能力训练提高层——拓展延伸展才华
★★5.如图14,△ABC中,∠C=90°,AC=3,BC=4,CD为AB边上的中线,点E、F分别在BC、AC上,且DE⊥DF,求EF的最小值。
图14
六、学习反思:
通过这节课的学习,你学习到什么新知识?获得了哪些经验?还有什么疑问?
学习反思 自我评价 小组评价 教师评价
(评价使用A、B、C、D四个等第)
应用
延伸
性质
定义
中线
一、学习内容:中考复习小专题:三角形的中线
二、学习目标:巩固、梳理与中线相关的知识点,认识相关知识点之间的联系,培养学生发散思维和根据题目相关条件进行综合分析、解决问题的能力。
教学重点: 梳理与中线相关的知识点,认识相关知识点之间的联系。
教学难点: 根据题目相关条件进行综合分析、解决问题的能力。
三、课堂前测:
(1) 叫做三角形的中线。
(2)如图1,△ABC中,AB=AC=13,BC=10,BC边上的中线长为 。
(3)如图2,△ABC中,∠C=90°,AC=6,BC=8,AB边上的中线长为 。
图1 图2 图3
(4) 如图3,已知AD为△ABC的中线,且S△ABC=10,则S△ABD= 。
(5) 如图4,△ABC的两条中线BD、CE相交于点G,点G叫做三角形的 ,DG:BG= 。
图4 图5
(6) 如图5,已知△ABC∽△A’B’C’,且相似比为2:3,AD、A’D’分别为△ABC、△A’B’C’的中线,那么AD:A’D’ = 。
四、学习过程:
1、知识结构梳理:
2、同伴项目式学习设计:
序号 学习项目 小组成员 学习方式 学习收获
1 课堂前测交流 合作探究
2 知识树梳理 合作探究
3、热点聚焦(师生共探):
例1 如图6,△ABC中,∠C=90°,AC=3,BC=4,CD为AB边上的中线。
(1) 求sin∠DCB的值; (2) 求sin∠ADC的值; (3)若点G为△ABC的重心,求DG的长。
图6 图7
例2 如图7,已知CD为△ABC的中线,且CD⊥CB, 若CD=2, CB=3, 求AC的长。
例3 如图8,已知△ABC中,D为AC上一点,BC=BD,点E、F分别为CD、AB的中点,求证:EF=AF
例4 如图9,已知∠ECF=90°,点A、B分别为CE、CF上的动点,AB=10,求AB边上的高CD的最大值。
图8 图9
五、随堂反馈:
(一)基础知识简单应用层——自主学习我最棒!
1. 如图10,已知点E、F分别为四边形ABCD的边BC、CD的中点,如果四边形ABCD的面积为18,那么四边形AECF的面积是多少?
图10 图11
2. 如图11,四边形ABCD中,∠ABC=∠ADC=90°,点E、F分别为对角线AC、BD的中点,求证:EF⊥BD
(二)具有一定开放性和思辨性的知识应用层——训练反馈显身手!
★3.如图12,已知AD为△ABC的中线,如果AB=3, AC=5, 那么AD的取值范围是多少?
图12 图13
★4.如图13,△ABC中,AB=AC=13,BC=10,点G为△ABC的重心,求BG的长。
(三)能力训练提高层——拓展延伸展才华
★★5.如图14,△ABC中,∠C=90°,AC=3,BC=4,CD为AB边上的中线,点E、F分别在BC、AC上,且DE⊥DF,求EF的最小值。
图14
六、学习反思:
通过这节课的学习,你学习到什么新知识?获得了哪些经验?还有什么疑问?
学习反思 自我评价 小组评价 教师评价
(评价使用A、B、C、D四个等第)
应用
延伸
性质
定义
中线
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
