山东省莱州市部分学校2021-2022学年下学期九年级期中考试数学试卷(图片版含答案)
文档属性
| 名称 | 山东省莱州市部分学校2021-2022学年下学期九年级期中考试数学试卷(图片版含答案) |

|
|
| 格式 | |||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 00:00:00 | ||
图片预览


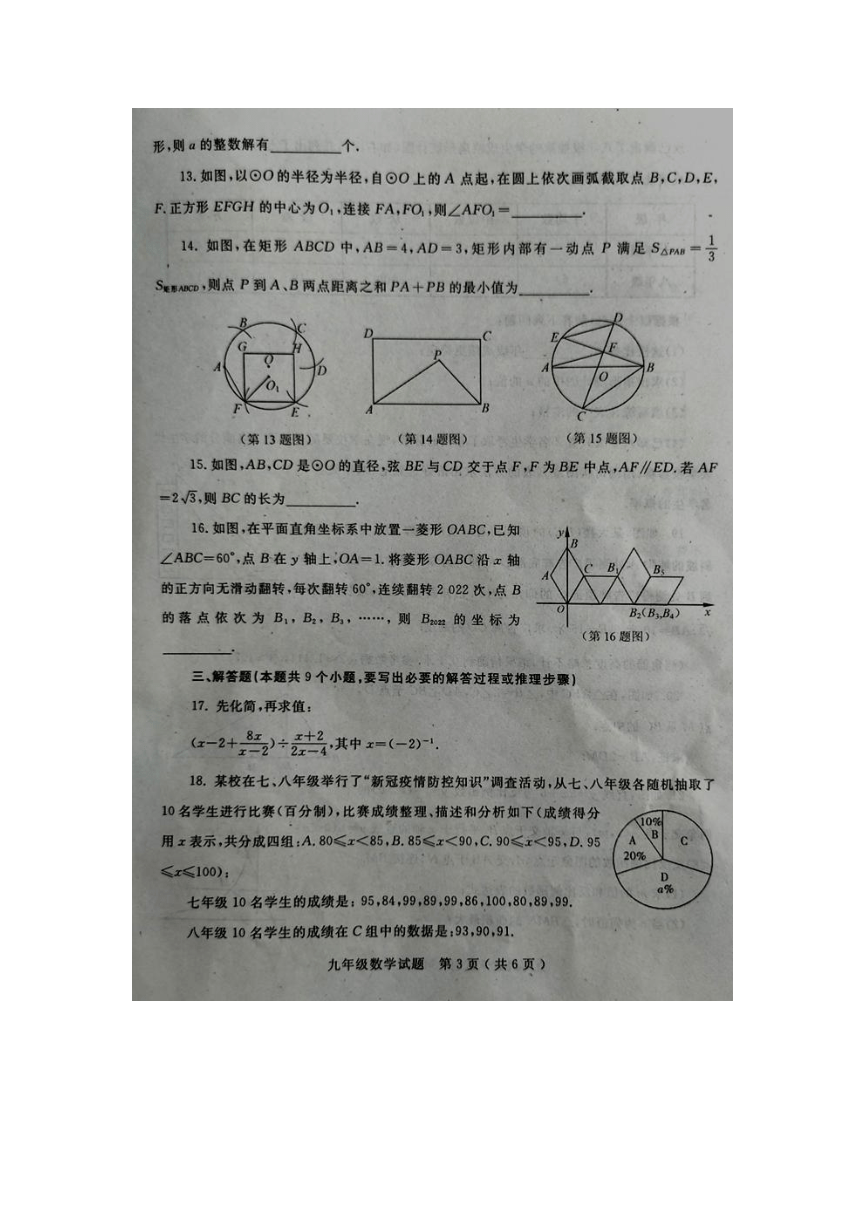
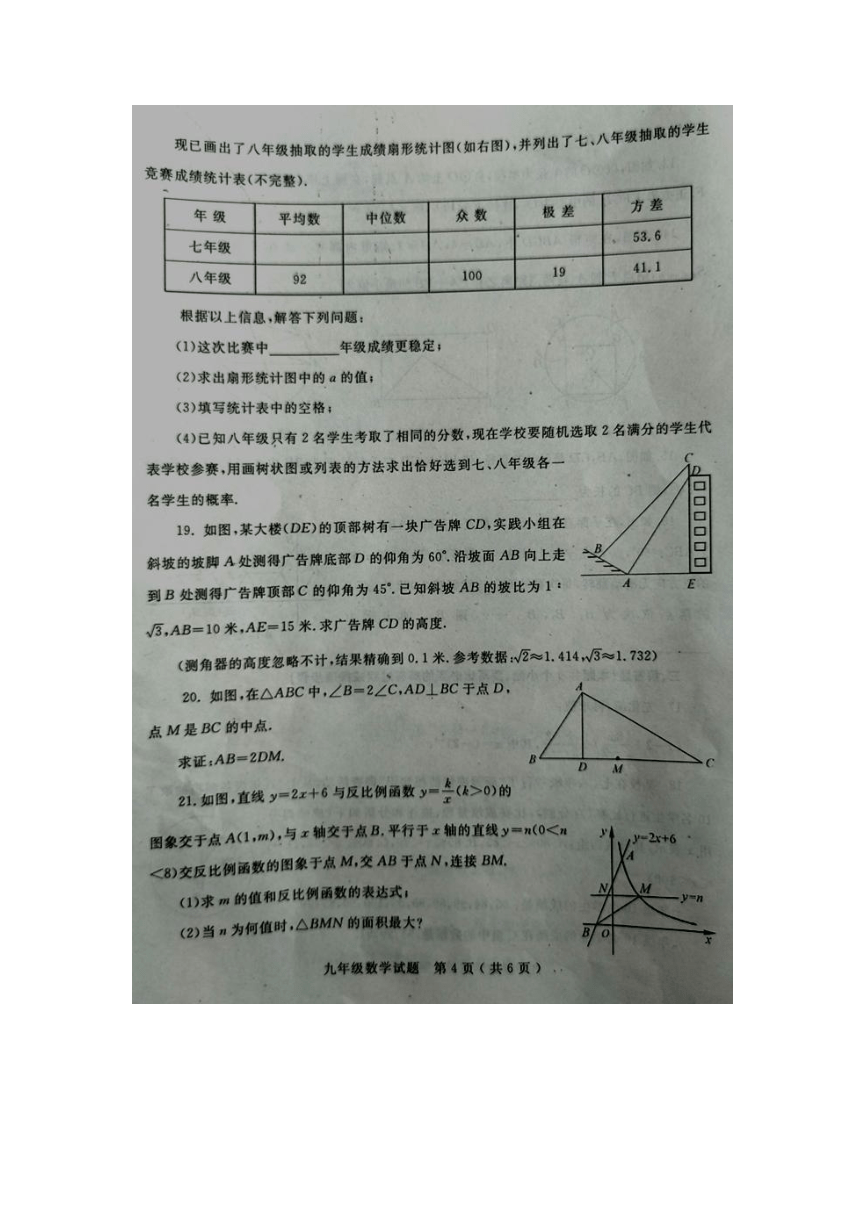

文档简介
2022 年春适应性检测
九年级数学试题参考答案及评分建议
一、选择题(本题共 10个小题,每小题 3分,共 30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D C B B D A A C
二、填空题(本题共 6 个小题,每小题 3分,共 18分)
11.k>-2 且 k≠-1 12.4 13.75° 14. 4 2 15.2 6 16.(1348, 3 )
三、解答题(本题共 9 个小题,共 72 分)
17.(本题共 5 分)
解:原式= …………………………………………………1 分
= ………………………………………………………………2 分
=2(x+2)
=2x+4. …………………………………………………………………………………4 分
当 x=﹣ 时,原式=﹣1+4=3.………………………………………………………5 分
18. (本题共 8 分)
(1)八 …………………………………………………………………………………1 分
(2)解:∵八年级 C 组有 3 个学生的成绩,
3
∴C 占总人数的 % 30%.
10
∴a% 100%-20%-10%-30%=40%,
∴a 40 . ……………………………………………………………………………2 分
(3)(每空 1 分,共 5 分)
年 级 平均数 中位数 众 数 极 差 方 差
七年级 92 92 99 20
八年级 92
(4)由题意可知,八年级满分有 2 人,若七年级满分 1 人和八年级满分 2 人分别用 A、
B、C 表示,树状图如下:
第 1 名 第 2 名 所有可能出现的结果
B (A,B)
A
C (A,C)
A (B,A)
开始 B
C (B,C)
A (C,A)
C
B (C,B)
共有 6 种等可能的结果,其中恰好选到七八年级各一名学生的情况有四种.
4 2
所以,P(恰好选到七八年级各一名学生)= . ………………………………8 分
6 3
19. (本题共 6 分)
解:过 B 作 BH⊥AE 于 H,作 BG⊥DE 于 G.
在 Rt△ABH 中, tan∠BAH= = ,
∴∠BAH=30°.
∴BH= AB=5,AH=AB·cos30°
3
=10× =5 .…………………………1 分
2
∵BH⊥HE,GE⊥HE,BG⊥DE,
∴四边形 BHEG 是矩形.
∴BG=HE=AH+AE=5 +15,GE=BH=5.…………………………………………2 分
在 Rt△BGC 中,∠CBG=45°,
∴CG=BG=5 +15.…………………………………………………………………3 分
∴CE=CG+GE=20+5 .
在 Rt△ADE 中,∠DAE=60°,AE=15,
∴DE=AE· tan 60°=15 .
∴CD=CE﹣DE=20+5 ﹣15 =20﹣10 ≈2.7(m).………………………5 分
答:广告牌 CD 高约 2.7 米. …………………………………………………………6 分
20. (本题共 6 分)
证明:取 AC 的中点 N,连接 MN,DN. ………………………………………………1 分
∵M 为 BC 的中点,
∴MN 为△ABC 的中位线,
∴MN∥AB,且 AB=2MN,……………………2 分
∴∠B=∠NMC.
∵∠B=2∠C,
∴∠NMC=2∠C.
∵DN 为 Rt△ADC 斜边上的中线,
∴DN=NC,
∴∠MDN=∠C.…………………………………………………………………………3 分
∴∠NMC=∠MDN+∠MND=2∠MDN,
∴∠MND=∠MDN,
∴DM=MN, ……………………………………………………………………………5 分
∴AB=2DM. ……………………………………………………………………………6 分
21. (本题共 7 分)
解:(1)∵直线 y=2x+6 经过点 A(1,m),
∴m=2×1+6=8.………………………………………………………………………1 分
∴A(1,8),
∵反比例函数经过点 A(1,8),
∴k=8,
∴反比例函数的表达式为 y= .………………………………………………………3 分
(2)由题意得,点 M,N 的坐标为 M( ,n),N( ,n), …………………4 分
∵0<n<8,
∴MN= ﹣ .
2
∴S△BMN= MN×n= ×( ﹣ )×n=﹣ (n﹣3) + , ……………6 分
∴n=3 时,△BMN 的面积最大,最大值为 .……………………………………7 分
22. (本题共 8 分) C
解:连接 OD,过点 C 作 CF⊥AB. ………………………1 分
O
∵AB 是⊙O 直径, ∴∠ACB=90°. A B
E F
1
∵∠CDB=∠CAB, tan CDB ,
2
BC 1
∴tan∠CAB= .……………………………………………………………D… …2 分
AC 2
2 2
∴设 BC= x,则 AC=2x, ∴AB= AC +BC = 5x .
1 5
∴OD= AB = x .……………………………………………………………………3 分
2 2
1 1
∵S△ABC= AC×BC= AB×CF, ∴2x·x= 5x ·CF,
2 2
2 5
∴CF= x .……………………………………………………………………………4 分
5
1
∵ = ∴∠ACD=∠BCD= ∠ACB=45°.
2
∴∠BOD=2∠BCD=90°.………………………………………………………………5 分
∵CF⊥AB, ∴∠CFE=90°. ∴∠CFE=∠BOD.
∵∠FEC=∠OED,
∴△CEF ∽△DEO. ……………………………………………………………………6 分
2 5
x
CE CF 4
∴ = = 5 = .……………………………………………………………7 分
DE DO 5 5
x
2
CE 4
∴ = . ……………………………………………………………………………8 分
CD 9
23. (本题共 10 分)
解:(1)设甲基地有蔬菜 a吨,乙基地有蔬菜b 吨,则
a b 500,
……………………………………………………………………1 分
a b 100.
a 200,
解得: …………………………………………………………………………2 分
b 300.
答:甲,乙基地分别有蔬菜 200 吨和 300 吨;…………………………………………3 分
(2)∵从乙基地运往 B 城蔬菜 x吨,
∴从乙基地运往 A 城蔬菜 (300 x) 吨,
从甲基地运往 B 城蔬菜 (260 x) 吨,
则从甲基地运往 A 城蔬菜 200-(260-x)= (x 60) 吨.
根据题意,得:
y 20(x 60) 25(260 x) 15(300 x) 30x 10x 9800 …………………………4 分
.
300 x 0
∵ 260 x 0
x 60 0
∴60 x 260 . …………………………………………………………………………5 分
∴y 与 x之间的函数关系式为 y 10x 9800(60 x 260);………………………6 分
(3)由题可得,
y 20(x 60) 25(260 x) 15(300 x) (30 a)x (10 a)x 9800 ………………7 分
当10 - a >0 ,即 0∴ x 60时, y最小 60 10 a 9800,
∵6(0 10 - a) 9800 10020 ,
19
∴0 < a ; …………………………………………………………………………8 分
3
当 10 -a=0,即 a=10 时,一次函数 y=(10-a)x+9800 的 y=9800,不合题意,舍去.
③当10 a 0,即 a 10时,一次函数 y=(10-a)x+9800 的 y 值随 x 的增大而减小,
∴ x 260 时, y最小 260 10 a 9800,
119 11
∵ 26(0 10 - a) 9800 10020 , ∴a 10 - ,
13 13
119
∵ <10 与 a 10不符,
13
∴这种情况不存在.………………………………………………………………………9 分
综上所述,a最大整数值为 6.…………………………………………………………10 分
24. (本题共 10 分)
(1)延长 DH 至点 H,使 DH=BE,连接 AH. ………………………………………1 分
∵四边形 ABCD 为正方形,
∴AB=AD,∠B=∠ADC=90°.∴∠B=∠ADH=90°. H
∵∠2=73°, ∴∠BAE=90°-∠2=17° . D A
1
在△ABE 和△ADH 中,
F 3
AB= AD Q
∠B=∠ADH=90 2
BE=DH C E B
P
∴△ABE≌△ADH. ………………………………………………………图…①… ……2 分
∴AE=AH,∠2=∠H=73°,∠BAE=∠DAH=17°.
∴∠HAF=∠DAH+∠1=17°+28°=45°.
∵∠EAF=90°-∠1-∠BAE=45° , ∴∠EAF=∠HAF.
又∵AE=AH,AF=AF,
∴△FAE≌△FAH.………………………………………………………………………3 分
∴∠3=∠AFH.
∵∠AFH=90°-∠1 =90°-28°=62°.
∴∠3==62°. ……………………………………………………………………………4 分
(2)AE 是∠FEB 的平分线,AF 是∠EFD 的平分线. ……………………………5 分
理由:延长 DH 至点 H,使 DH=BE,连接 AH .
同(1)可证△ABE≌△ADH.………………………6 分
H
D 4 A
3
2
Q F 1
∴AE=AH,∠AEB=∠H,∠1=∠4.
∵∠2=45°,
∴∠1+∠3=90°-∠2=45°,
∴∠4+∠3=90°-∠2=45° ,
即∠HAF=45°.
∴∠2=∠HAF.
又∵AE=AH, AF=AF,
∴△FAE≌△FAH.………………………………………………………………………7 分
∴∠AFE=∠AFH,∠AEF=∠H. ∴∠AEB=∠AEF.
∴AE 平分∠FEB ,AF 平分∠EFD.……………………………………………………8 分
(3)AE 仍然是∠FEB 的平分线,AF 不是∠EFD 的平分线. ……………………10 分
25. (本题共 12 分)
2
解:(1)∵抛物线 y= x +c 经过点 A(4,3),
∴3= ×16+c,
∴c=﹣1. ………………………………………………………………………………2 分
2
∴抛物线表达式为 y= x -1,顶点 B(0,-1). ……………………………………3 分
(2)证明:过 P 作 PH⊥l,垂足为 H.
设点 坐标( , 2P m m -1), y
∵ 2 2PH= m -1-(-2)= m +1,…………………4 分
3 A
, …………6 分 P
1 1
PO m2 ( m2 1)2 m2 1
4 4 O 4 x
B
∴PO=PH. H l
∴经过点 O 的⊙P 与直线 l 相切. ………………7 分
图①
(3)存在.………………………………………………………………………………8 分
理由:
∵BC= = ,AC= = ,AB= =4 .………9 分
∴BC=AC.
由(2)知,PO=PH,
PH HO
∴当 时,以 P,O,H 为顶点的三角形与△ABC 相似.
BC AB
2 1 2
同(2)设点 P(m, m -1),则 H(m,-2), PH= m +1,
4
2
∴HO= m + ( -2 )2 = m2 + 4 ,
1
m2 +1 m24 +4
∴ = .
10 4 2
解得 m=±1. …………………………………………………………………………11 分
∴点 P 坐标(1,﹣ )或(﹣1,﹣ ). …………………………………………12 分
y
3 A C
4
O x
B
l
图②
九年级数学试题参考答案及评分建议
一、选择题(本题共 10个小题,每小题 3分,共 30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D C B B D A A C
二、填空题(本题共 6 个小题,每小题 3分,共 18分)
11.k>-2 且 k≠-1 12.4 13.75° 14. 4 2 15.2 6 16.(1348, 3 )
三、解答题(本题共 9 个小题,共 72 分)
17.(本题共 5 分)
解:原式= …………………………………………………1 分
= ………………………………………………………………2 分
=2(x+2)
=2x+4. …………………………………………………………………………………4 分
当 x=﹣ 时,原式=﹣1+4=3.………………………………………………………5 分
18. (本题共 8 分)
(1)八 …………………………………………………………………………………1 分
(2)解:∵八年级 C 组有 3 个学生的成绩,
3
∴C 占总人数的 % 30%.
10
∴a% 100%-20%-10%-30%=40%,
∴a 40 . ……………………………………………………………………………2 分
(3)(每空 1 分,共 5 分)
年 级 平均数 中位数 众 数 极 差 方 差
七年级 92 92 99 20
八年级 92
(4)由题意可知,八年级满分有 2 人,若七年级满分 1 人和八年级满分 2 人分别用 A、
B、C 表示,树状图如下:
第 1 名 第 2 名 所有可能出现的结果
B (A,B)
A
C (A,C)
A (B,A)
开始 B
C (B,C)
A (C,A)
C
B (C,B)
共有 6 种等可能的结果,其中恰好选到七八年级各一名学生的情况有四种.
4 2
所以,P(恰好选到七八年级各一名学生)= . ………………………………8 分
6 3
19. (本题共 6 分)
解:过 B 作 BH⊥AE 于 H,作 BG⊥DE 于 G.
在 Rt△ABH 中, tan∠BAH= = ,
∴∠BAH=30°.
∴BH= AB=5,AH=AB·cos30°
3
=10× =5 .…………………………1 分
2
∵BH⊥HE,GE⊥HE,BG⊥DE,
∴四边形 BHEG 是矩形.
∴BG=HE=AH+AE=5 +15,GE=BH=5.…………………………………………2 分
在 Rt△BGC 中,∠CBG=45°,
∴CG=BG=5 +15.…………………………………………………………………3 分
∴CE=CG+GE=20+5 .
在 Rt△ADE 中,∠DAE=60°,AE=15,
∴DE=AE· tan 60°=15 .
∴CD=CE﹣DE=20+5 ﹣15 =20﹣10 ≈2.7(m).………………………5 分
答:广告牌 CD 高约 2.7 米. …………………………………………………………6 分
20. (本题共 6 分)
证明:取 AC 的中点 N,连接 MN,DN. ………………………………………………1 分
∵M 为 BC 的中点,
∴MN 为△ABC 的中位线,
∴MN∥AB,且 AB=2MN,……………………2 分
∴∠B=∠NMC.
∵∠B=2∠C,
∴∠NMC=2∠C.
∵DN 为 Rt△ADC 斜边上的中线,
∴DN=NC,
∴∠MDN=∠C.…………………………………………………………………………3 分
∴∠NMC=∠MDN+∠MND=2∠MDN,
∴∠MND=∠MDN,
∴DM=MN, ……………………………………………………………………………5 分
∴AB=2DM. ……………………………………………………………………………6 分
21. (本题共 7 分)
解:(1)∵直线 y=2x+6 经过点 A(1,m),
∴m=2×1+6=8.………………………………………………………………………1 分
∴A(1,8),
∵反比例函数经过点 A(1,8),
∴k=8,
∴反比例函数的表达式为 y= .………………………………………………………3 分
(2)由题意得,点 M,N 的坐标为 M( ,n),N( ,n), …………………4 分
∵0<n<8,
∴MN= ﹣ .
2
∴S△BMN= MN×n= ×( ﹣ )×n=﹣ (n﹣3) + , ……………6 分
∴n=3 时,△BMN 的面积最大,最大值为 .……………………………………7 分
22. (本题共 8 分) C
解:连接 OD,过点 C 作 CF⊥AB. ………………………1 分
O
∵AB 是⊙O 直径, ∴∠ACB=90°. A B
E F
1
∵∠CDB=∠CAB, tan CDB ,
2
BC 1
∴tan∠CAB= .……………………………………………………………D… …2 分
AC 2
2 2
∴设 BC= x,则 AC=2x, ∴AB= AC +BC = 5x .
1 5
∴OD= AB = x .……………………………………………………………………3 分
2 2
1 1
∵S△ABC= AC×BC= AB×CF, ∴2x·x= 5x ·CF,
2 2
2 5
∴CF= x .……………………………………………………………………………4 分
5
1
∵ = ∴∠ACD=∠BCD= ∠ACB=45°.
2
∴∠BOD=2∠BCD=90°.………………………………………………………………5 分
∵CF⊥AB, ∴∠CFE=90°. ∴∠CFE=∠BOD.
∵∠FEC=∠OED,
∴△CEF ∽△DEO. ……………………………………………………………………6 分
2 5
x
CE CF 4
∴ = = 5 = .……………………………………………………………7 分
DE DO 5 5
x
2
CE 4
∴ = . ……………………………………………………………………………8 分
CD 9
23. (本题共 10 分)
解:(1)设甲基地有蔬菜 a吨,乙基地有蔬菜b 吨,则
a b 500,
……………………………………………………………………1 分
a b 100.
a 200,
解得: …………………………………………………………………………2 分
b 300.
答:甲,乙基地分别有蔬菜 200 吨和 300 吨;…………………………………………3 分
(2)∵从乙基地运往 B 城蔬菜 x吨,
∴从乙基地运往 A 城蔬菜 (300 x) 吨,
从甲基地运往 B 城蔬菜 (260 x) 吨,
则从甲基地运往 A 城蔬菜 200-(260-x)= (x 60) 吨.
根据题意,得:
y 20(x 60) 25(260 x) 15(300 x) 30x 10x 9800 …………………………4 分
.
300 x 0
∵ 260 x 0
x 60 0
∴60 x 260 . …………………………………………………………………………5 分
∴y 与 x之间的函数关系式为 y 10x 9800(60 x 260);………………………6 分
(3)由题可得,
y 20(x 60) 25(260 x) 15(300 x) (30 a)x (10 a)x 9800 ………………7 分
当10 - a >0 ,即 0
∵6(0 10 - a) 9800 10020 ,
19
∴0 < a ; …………………………………………………………………………8 分
3
当 10 -a=0,即 a=10 时,一次函数 y=(10-a)x+9800 的 y=9800,不合题意,舍去.
③当10 a 0,即 a 10时,一次函数 y=(10-a)x+9800 的 y 值随 x 的增大而减小,
∴ x 260 时, y最小 260 10 a 9800,
119 11
∵ 26(0 10 - a) 9800 10020 , ∴a 10 - ,
13 13
119
∵ <10 与 a 10不符,
13
∴这种情况不存在.………………………………………………………………………9 分
综上所述,a最大整数值为 6.…………………………………………………………10 分
24. (本题共 10 分)
(1)延长 DH 至点 H,使 DH=BE,连接 AH. ………………………………………1 分
∵四边形 ABCD 为正方形,
∴AB=AD,∠B=∠ADC=90°.∴∠B=∠ADH=90°. H
∵∠2=73°, ∴∠BAE=90°-∠2=17° . D A
1
在△ABE 和△ADH 中,
F 3
AB= AD Q
∠B=∠ADH=90 2
BE=DH C E B
P
∴△ABE≌△ADH. ………………………………………………………图…①… ……2 分
∴AE=AH,∠2=∠H=73°,∠BAE=∠DAH=17°.
∴∠HAF=∠DAH+∠1=17°+28°=45°.
∵∠EAF=90°-∠1-∠BAE=45° , ∴∠EAF=∠HAF.
又∵AE=AH,AF=AF,
∴△FAE≌△FAH.………………………………………………………………………3 分
∴∠3=∠AFH.
∵∠AFH=90°-∠1 =90°-28°=62°.
∴∠3==62°. ……………………………………………………………………………4 分
(2)AE 是∠FEB 的平分线,AF 是∠EFD 的平分线. ……………………………5 分
理由:延长 DH 至点 H,使 DH=BE,连接 AH .
同(1)可证△ABE≌△ADH.………………………6 分
H
D 4 A
3
2
Q F 1
∴AE=AH,∠AEB=∠H,∠1=∠4.
∵∠2=45°,
∴∠1+∠3=90°-∠2=45°,
∴∠4+∠3=90°-∠2=45° ,
即∠HAF=45°.
∴∠2=∠HAF.
又∵AE=AH, AF=AF,
∴△FAE≌△FAH.………………………………………………………………………7 分
∴∠AFE=∠AFH,∠AEF=∠H. ∴∠AEB=∠AEF.
∴AE 平分∠FEB ,AF 平分∠EFD.……………………………………………………8 分
(3)AE 仍然是∠FEB 的平分线,AF 不是∠EFD 的平分线. ……………………10 分
25. (本题共 12 分)
2
解:(1)∵抛物线 y= x +c 经过点 A(4,3),
∴3= ×16+c,
∴c=﹣1. ………………………………………………………………………………2 分
2
∴抛物线表达式为 y= x -1,顶点 B(0,-1). ……………………………………3 分
(2)证明:过 P 作 PH⊥l,垂足为 H.
设点 坐标( , 2P m m -1), y
∵ 2 2PH= m -1-(-2)= m +1,…………………4 分
3 A
, …………6 分 P
1 1
PO m2 ( m2 1)2 m2 1
4 4 O 4 x
B
∴PO=PH. H l
∴经过点 O 的⊙P 与直线 l 相切. ………………7 分
图①
(3)存在.………………………………………………………………………………8 分
理由:
∵BC= = ,AC= = ,AB= =4 .………9 分
∴BC=AC.
由(2)知,PO=PH,
PH HO
∴当 时,以 P,O,H 为顶点的三角形与△ABC 相似.
BC AB
2 1 2
同(2)设点 P(m, m -1),则 H(m,-2), PH= m +1,
4
2
∴HO= m + ( -2 )2 = m2 + 4 ,
1
m2 +1 m24 +4
∴ = .
10 4 2
解得 m=±1. …………………………………………………………………………11 分
∴点 P 坐标(1,﹣ )或(﹣1,﹣ ). …………………………………………12 分
y
3 A C
4
O x
B
l
图②
同课章节目录
