四年级下学期数学《认识三角形和四边形》单元分层作业(无答案)北师大版
文档属性
| 名称 | 四年级下学期数学《认识三角形和四边形》单元分层作业(无答案)北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 522.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 12:09:15 | ||
图片预览


文档简介
单元名称 认识三角形和四边形 课题 图形分类 节次 第二单元第1课时
作业类型 作业内容 设计意图
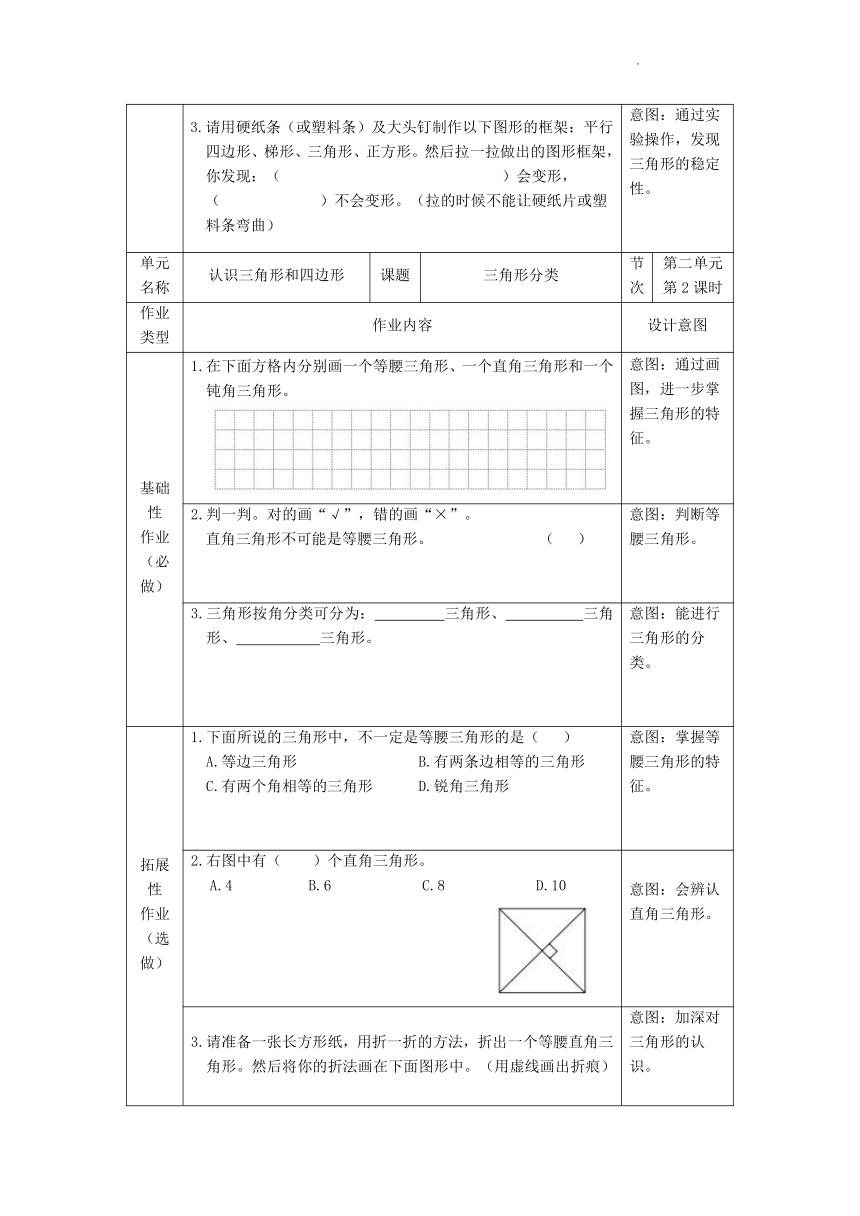
基础性 作业 (必做) 1.按要求将图形对应的字母填在括号里。 上面图形中,平面图形有( ),立体图形有 ( )。在平面图形中,( )是直线图形, ( )是曲线图形。 意图:能对图形进行分类。
2.观察下面图形,图中有( )个梯形,有( )个三角形,有( )个平行四边形。 意图:能正确认识、数图形。
3.围篱笆。 意图:知道三角形的稳定性。
拓展性 作业 (选做) 1.按要求分一分,并说说你的分类的方法。 意图:能按要求对图形进行分类。
2.请在下面图形内画一条线段,将图形分成一个平行四边形和 一个三角形。 意图:运用图形特征,按要求画图形。
3.请用硬纸条(或塑料条)及大头钉制作以下图形的框架:平行四边形、梯形、三角形、正方形。然后拉一拉做出的图形框架,你发现:( )会变形,( )不会变形。(拉的时候不能让硬纸片或塑料条弯曲) 意图:通过实验操作,发现三角形的稳定性。
单元名称 认识三角形和四边形 课题 三角形分类 节次 第二单元第2课时
作业类型 作业内容 设计意图
基础性 作业 (必做) 1.在下面方格内分别画一个等腰三角形、一个直角三角形和一个钝角三角形。 意图:通过画图,进一步掌握三角形的特征。
2.判一判。对的画“√”,错的画“×”。 直角三角形不可能是等腰三角形。 ( ) 意图:判断等腰三角形。
3.三角形按角分类可分为: 三角形、 三角形、 三角形。 意图:能进行三角形的分类。
拓展性 作业 (选做) 1.下面所说的三角形中,不一定是等腰三角形的是( ) A.等边三角形 B.有两条边相等的三角形 C.有两个角相等的三角形 D.锐角三角形 意图:掌握等腰三角形的特征。
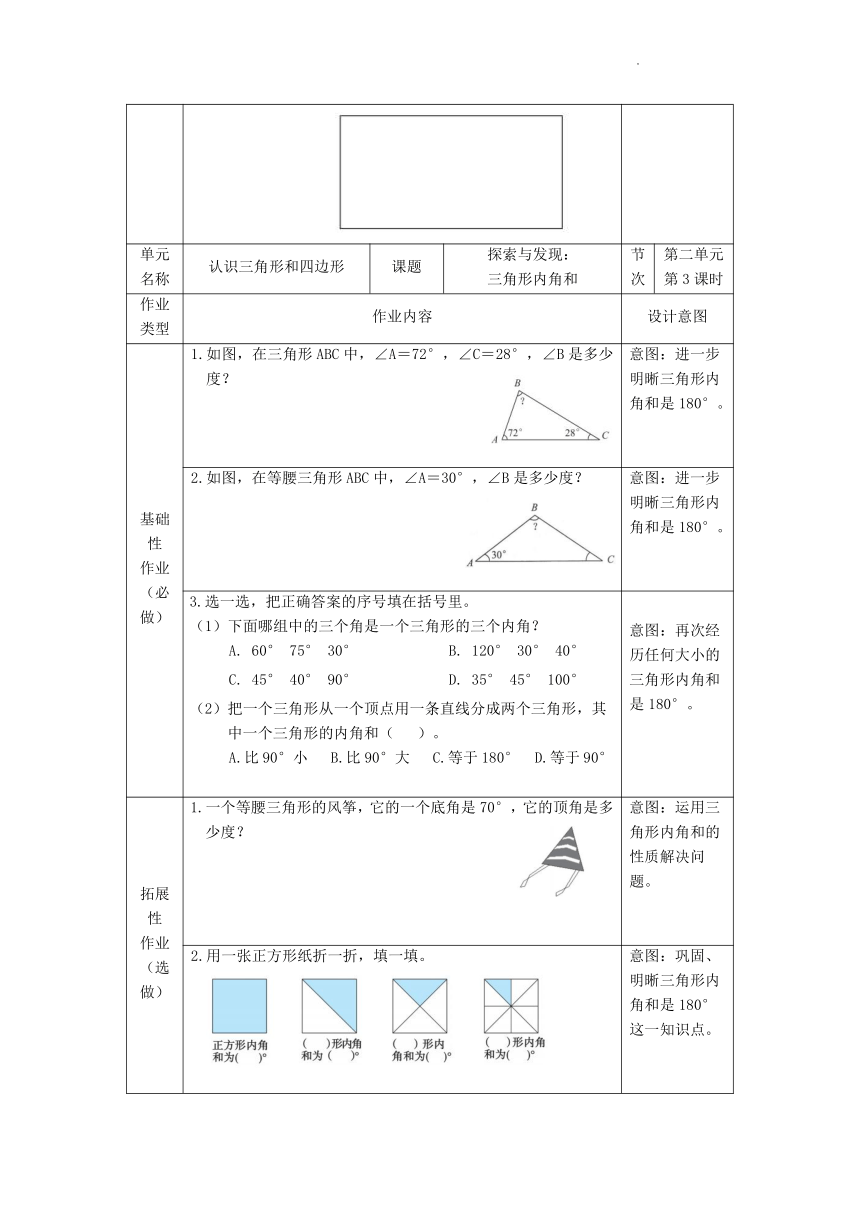
2.右图中有( )个直角三角形。 A.4 B.6 C.8 D.10 意图:会辨认直角三角形。
3.请准备一张长方形纸,用折一折的方法,折出一个等腰直角三角形。然后将你的折法画在下面图形中。(用虚线画出折痕) 意图:加深对三角形的认识。
单元名称 认识三角形和四边形 课题 探索与发现: 三角形内角和 节次 第二单元第3课时
作业类型 作业内容 设计意图
基础性 作业 (必做) 1.如图,在三角形ABC中,∠A=72°,∠C=28°,∠B是多少度? 意图:进一步明晰三角形内角和是180°。
2.如图,在等腰三角形ABC中,∠A=30°,∠B是多少度? 意图:进一步明晰三角形内角和是180°。
3.选一选,把正确答案的序号填在括号里。 (1)下面哪组中的三个角是一个三角形的三个内角? A. 60° 75° 30° B. 120° 30° 40° C. 45° 40° 90° D. 35° 45° 100° (2)把一个三角形从一个顶点用一条直线分成两个三角形,其中一个三角形的内角和( )。 A.比90°小 B.比90°大 C.等于180° D.等于90° 意图:再次经历任何大小的三角形内角和是180°。
拓展性 作业 (选做) 1.一个等腰三角形的风筝,它的一个底角是70°,它的顶角是多少度? 意图:运用三角形内角和的性质解决问题。
2.用一张正方形纸折一折,填一填。 意图:巩固、明晰三角形内角和是180°这一知识点。
3.鹏鹏把△ABC分成了△ABD和△ADC,你知道哪一个三角形的内角和比较大?想一想,说一说。 意图:任何大小的三角形内角和是180°。
单元名称 认识三角形和四边形 课题 探索与发现: 三角形内角和(试一试) 节次 第二单元第4课时
作业类型 作业内容 设计意图
基础性 作业 (必做) 1.选一选,把正确答案的序号填在括号里。 (1)钝角三角形的两个锐角之和( )。 A.大于90° B.小于90 C.等于90° D.小于60° (2)一个三角形中,有两条边相等,有一个内角是60°,这个三角形( )。 A. 一定是钝角三角形 B.一定是等边三角形 C.一定是直角三角形 D.不能确定是什么三角形 意图:运用三角形内角和和分类特征进行推理。
2.调皮的淘气不小心将同学画的三角形弄脏了,被遮住的那两个角的度数可能是( )。并简要说说你的理由。 意图:综合运用三角形内角和进行推理。
3.判一判。 (1)有一个角是60°的三角形一定是等边三角形。 ( ) (2)有两个角是锐角的三角形一定是锐角三角形。 ( ) (3)直角三角形中的两个锐角的和正好是90°。 ( ) (4)等腰三角形一定是锐角三角形。 ( ) 意图:运用三角形内角和等于180°解决问题。
拓展性 作业 (选做) 1.下图是3块三角形玻璃破碎后的碎片,你知道它们原来各是什么三角形吗?想 一想,写一写。 意图:巩固三角形内角和等于180°。
2.先写出下面各三角形的名字,再填一填。 至少用( )个等腰直角三角形能拼成一个正方形。 至少用( )个( )能拼成一个长方形。 至少用( )个( )能拼成一个平行四边形。 至少用( )个( )能拼成一个梯形。 意图:复习各类三角形特征并与四边形建立联系。
3.利用“三角形内角和是180°”这一结论,你能计算下面图形的内角和吗?试着画一画,再算一算。 意图:三角形内角和的拓展运用。
单元名称 认识三角形和四边形 课题 探索与发现: 三角形边的关系 节次 第二单元第5课时
作业类型 作业内容 设计意图
基础性 作业 (必做) 1.下面能围成三角形的一组数据是( )。 A.3厘米 5厘米 9厘米 B.4厘米 6厘米 9厘米 C.4.3厘米 5.2厘米 10厘米 D.2.5分米 3.5分米 7分米 意图:进一步认识三边关系。
2.观察右边三角形,然后在○里填上“>”“<”或“=”。 意图:运用三边关系。
3.有五根小棒a,b,c,d,e,长度分别为3厘米、5厘米、7厘米、8厘米、10厘米。任意取出其中的三根,可以摆成几种不同的三角形?请照例子写在下面。(能写几种就写几种) 意图:运用三角形三边关系判断3根小棒能否摆出三角形。
拓展性 作业 (选做) 1.用下面的小棒摆三角形。 (1)你能摆出几种等边三角形呢?摆一摆,画一画。 (2)用这9根小棒摆成一个等边三角形和两个等腰三角形,摆 一摆,画一画。 意图:重在操作的探索活动。
2.判一判。 (1)三根同样长的小棒一定可以围成一个三角形。 ( ) (2)在三角形中,任意两边之和一定大于或等于第三 三边。( ) (3)一个三角形的两条边分别为3厘米、2厘米,那么第三条边可能是1厘米。 ( ) (4)等边三角形的三个角相等,三条边也相等。 ( ) 意图:综合练习三边关系。
3.要想钉成三角形,第三根木条最短( )厘米,最长( )厘米。(木条长度取整厘米数) 意图:运用三角形三边关系解决综合问题。
单元名称 认识三角形和四边形 课题 四边形分类 节次 第二单元 第6课时
作业类型 作业内容 设计意图
基础性 作业 (必做) 1.找房子。把图形序号填在相应的房子里。 意图:进一步明晰平行四边形和梯形的特征。
2.判一判,对的画“√”,错的画“×”。 (1)有一组对边平行的四边形就是平行四边形。 ( ) (2)长方形、正方形都是特殊的平行四边形。 ( ) (3)四边相等的平行四边形一定是正方形。 ( ) 意图:巩固长方形、正方形和平行四边形之间的联系。
3.选一选。把正确答案的序号填在括号里。 (1)下列图形中不属于平行四边形的是( )。 (2)下面各图形中具有稳定性的是( )。 A.平行四边形 B.梯形 C.三角形 D.正方形 意图:进一步认识平行四边形。
拓展性 作业 (选做) 1.准备三张长方形纸片和一把剪刀,沿着直线剪一刀,剪出符合要求的图形。在图中画出你的剪法。 意图:既清晰图形特征,又为后面图形变换探索面积公式以及解决相关问题做铺垫。
2.想一想,填一填。 量一量上面每个梯形的腰,发现它的两条腰( ),这样的梯形就是( )梯形。 意图:通过量比活动,进一步认识梯形。
3.你知道正方形、长方形、平行四边形、梯形的特征吗?在 里打“√”,并与同伴说说。 意图:学生体会到已学习的图形之间的联系。
单元名称 认识三角形 和四边形 课题 练习二 节次 第二单元第7课时
作业类型 作业内容 设计意图
基础性 作业 (必做) 1.填一填。 (1)锐角三角形有( )个角是锐角;直角三角形有( )个角是直角;钝角三角形有( )个角是钝角。 (2)在30°, 100°, 1°, 89°, 91°和300°六个角中,( )角是锐角,( )的角是钝角。 (3)一个三角形的两条边分别是8厘米和5厘米,第三条边一定比( )米长,比( )厘米短。 意图:综合运用三角形内角和、三角形边的关系解决问题。
2.选一选。把正确答案的序号填在括号里。 (1)一个三角形中,有一个角是65°,另外的两个角可能是( )。 A.85°,20° B. 45°, 80° C. 55°, 60° (2)一个三角形的三个内角都不小于60° ,这个三角形一定是( )三角形。 A.钝角 B. 直角 C. 等边 (3)用放大5倍的放大镜看一个三角形,这个三角形内角和是( ) A.360° B.900° C. 180° 意图:综合运用三角形内角和、三角形分类解决问题。
3.在点子图上按要求画图。 意图:通过画图形,进一步加深对图形的特征的认识。
拓展性 作业 (选做) 1.直角三角形中,∠A的度数是多少? 意图:综合运用三角形内角和。
2.钝角三角形中已知∠A=140°∠C=25°,求∠B的度数。 意图:综合运用三角形内角和。
3.求出下图中∠1,∠2,∠3的度数。 意图:综合运用三角形内角和。
作业类型 作业内容 设计意图
基础性 作业 (必做) 1.按要求将图形对应的字母填在括号里。 上面图形中,平面图形有( ),立体图形有 ( )。在平面图形中,( )是直线图形, ( )是曲线图形。 意图:能对图形进行分类。
2.观察下面图形,图中有( )个梯形,有( )个三角形,有( )个平行四边形。 意图:能正确认识、数图形。
3.围篱笆。 意图:知道三角形的稳定性。
拓展性 作业 (选做) 1.按要求分一分,并说说你的分类的方法。 意图:能按要求对图形进行分类。
2.请在下面图形内画一条线段,将图形分成一个平行四边形和 一个三角形。 意图:运用图形特征,按要求画图形。
3.请用硬纸条(或塑料条)及大头钉制作以下图形的框架:平行四边形、梯形、三角形、正方形。然后拉一拉做出的图形框架,你发现:( )会变形,( )不会变形。(拉的时候不能让硬纸片或塑料条弯曲) 意图:通过实验操作,发现三角形的稳定性。
单元名称 认识三角形和四边形 课题 三角形分类 节次 第二单元第2课时
作业类型 作业内容 设计意图
基础性 作业 (必做) 1.在下面方格内分别画一个等腰三角形、一个直角三角形和一个钝角三角形。 意图:通过画图,进一步掌握三角形的特征。
2.判一判。对的画“√”,错的画“×”。 直角三角形不可能是等腰三角形。 ( ) 意图:判断等腰三角形。
3.三角形按角分类可分为: 三角形、 三角形、 三角形。 意图:能进行三角形的分类。
拓展性 作业 (选做) 1.下面所说的三角形中,不一定是等腰三角形的是( ) A.等边三角形 B.有两条边相等的三角形 C.有两个角相等的三角形 D.锐角三角形 意图:掌握等腰三角形的特征。
2.右图中有( )个直角三角形。 A.4 B.6 C.8 D.10 意图:会辨认直角三角形。
3.请准备一张长方形纸,用折一折的方法,折出一个等腰直角三角形。然后将你的折法画在下面图形中。(用虚线画出折痕) 意图:加深对三角形的认识。
单元名称 认识三角形和四边形 课题 探索与发现: 三角形内角和 节次 第二单元第3课时
作业类型 作业内容 设计意图
基础性 作业 (必做) 1.如图,在三角形ABC中,∠A=72°,∠C=28°,∠B是多少度? 意图:进一步明晰三角形内角和是180°。
2.如图,在等腰三角形ABC中,∠A=30°,∠B是多少度? 意图:进一步明晰三角形内角和是180°。
3.选一选,把正确答案的序号填在括号里。 (1)下面哪组中的三个角是一个三角形的三个内角? A. 60° 75° 30° B. 120° 30° 40° C. 45° 40° 90° D. 35° 45° 100° (2)把一个三角形从一个顶点用一条直线分成两个三角形,其中一个三角形的内角和( )。 A.比90°小 B.比90°大 C.等于180° D.等于90° 意图:再次经历任何大小的三角形内角和是180°。
拓展性 作业 (选做) 1.一个等腰三角形的风筝,它的一个底角是70°,它的顶角是多少度? 意图:运用三角形内角和的性质解决问题。
2.用一张正方形纸折一折,填一填。 意图:巩固、明晰三角形内角和是180°这一知识点。
3.鹏鹏把△ABC分成了△ABD和△ADC,你知道哪一个三角形的内角和比较大?想一想,说一说。 意图:任何大小的三角形内角和是180°。
单元名称 认识三角形和四边形 课题 探索与发现: 三角形内角和(试一试) 节次 第二单元第4课时
作业类型 作业内容 设计意图
基础性 作业 (必做) 1.选一选,把正确答案的序号填在括号里。 (1)钝角三角形的两个锐角之和( )。 A.大于90° B.小于90 C.等于90° D.小于60° (2)一个三角形中,有两条边相等,有一个内角是60°,这个三角形( )。 A. 一定是钝角三角形 B.一定是等边三角形 C.一定是直角三角形 D.不能确定是什么三角形 意图:运用三角形内角和和分类特征进行推理。
2.调皮的淘气不小心将同学画的三角形弄脏了,被遮住的那两个角的度数可能是( )。并简要说说你的理由。 意图:综合运用三角形内角和进行推理。
3.判一判。 (1)有一个角是60°的三角形一定是等边三角形。 ( ) (2)有两个角是锐角的三角形一定是锐角三角形。 ( ) (3)直角三角形中的两个锐角的和正好是90°。 ( ) (4)等腰三角形一定是锐角三角形。 ( ) 意图:运用三角形内角和等于180°解决问题。
拓展性 作业 (选做) 1.下图是3块三角形玻璃破碎后的碎片,你知道它们原来各是什么三角形吗?想 一想,写一写。 意图:巩固三角形内角和等于180°。
2.先写出下面各三角形的名字,再填一填。 至少用( )个等腰直角三角形能拼成一个正方形。 至少用( )个( )能拼成一个长方形。 至少用( )个( )能拼成一个平行四边形。 至少用( )个( )能拼成一个梯形。 意图:复习各类三角形特征并与四边形建立联系。
3.利用“三角形内角和是180°”这一结论,你能计算下面图形的内角和吗?试着画一画,再算一算。 意图:三角形内角和的拓展运用。
单元名称 认识三角形和四边形 课题 探索与发现: 三角形边的关系 节次 第二单元第5课时
作业类型 作业内容 设计意图
基础性 作业 (必做) 1.下面能围成三角形的一组数据是( )。 A.3厘米 5厘米 9厘米 B.4厘米 6厘米 9厘米 C.4.3厘米 5.2厘米 10厘米 D.2.5分米 3.5分米 7分米 意图:进一步认识三边关系。
2.观察右边三角形,然后在○里填上“>”“<”或“=”。 意图:运用三边关系。
3.有五根小棒a,b,c,d,e,长度分别为3厘米、5厘米、7厘米、8厘米、10厘米。任意取出其中的三根,可以摆成几种不同的三角形?请照例子写在下面。(能写几种就写几种) 意图:运用三角形三边关系判断3根小棒能否摆出三角形。
拓展性 作业 (选做) 1.用下面的小棒摆三角形。 (1)你能摆出几种等边三角形呢?摆一摆,画一画。 (2)用这9根小棒摆成一个等边三角形和两个等腰三角形,摆 一摆,画一画。 意图:重在操作的探索活动。
2.判一判。 (1)三根同样长的小棒一定可以围成一个三角形。 ( ) (2)在三角形中,任意两边之和一定大于或等于第三 三边。( ) (3)一个三角形的两条边分别为3厘米、2厘米,那么第三条边可能是1厘米。 ( ) (4)等边三角形的三个角相等,三条边也相等。 ( ) 意图:综合练习三边关系。
3.要想钉成三角形,第三根木条最短( )厘米,最长( )厘米。(木条长度取整厘米数) 意图:运用三角形三边关系解决综合问题。
单元名称 认识三角形和四边形 课题 四边形分类 节次 第二单元 第6课时
作业类型 作业内容 设计意图
基础性 作业 (必做) 1.找房子。把图形序号填在相应的房子里。 意图:进一步明晰平行四边形和梯形的特征。
2.判一判,对的画“√”,错的画“×”。 (1)有一组对边平行的四边形就是平行四边形。 ( ) (2)长方形、正方形都是特殊的平行四边形。 ( ) (3)四边相等的平行四边形一定是正方形。 ( ) 意图:巩固长方形、正方形和平行四边形之间的联系。
3.选一选。把正确答案的序号填在括号里。 (1)下列图形中不属于平行四边形的是( )。 (2)下面各图形中具有稳定性的是( )。 A.平行四边形 B.梯形 C.三角形 D.正方形 意图:进一步认识平行四边形。
拓展性 作业 (选做) 1.准备三张长方形纸片和一把剪刀,沿着直线剪一刀,剪出符合要求的图形。在图中画出你的剪法。 意图:既清晰图形特征,又为后面图形变换探索面积公式以及解决相关问题做铺垫。
2.想一想,填一填。 量一量上面每个梯形的腰,发现它的两条腰( ),这样的梯形就是( )梯形。 意图:通过量比活动,进一步认识梯形。
3.你知道正方形、长方形、平行四边形、梯形的特征吗?在 里打“√”,并与同伴说说。 意图:学生体会到已学习的图形之间的联系。
单元名称 认识三角形 和四边形 课题 练习二 节次 第二单元第7课时
作业类型 作业内容 设计意图
基础性 作业 (必做) 1.填一填。 (1)锐角三角形有( )个角是锐角;直角三角形有( )个角是直角;钝角三角形有( )个角是钝角。 (2)在30°, 100°, 1°, 89°, 91°和300°六个角中,( )角是锐角,( )的角是钝角。 (3)一个三角形的两条边分别是8厘米和5厘米,第三条边一定比( )米长,比( )厘米短。 意图:综合运用三角形内角和、三角形边的关系解决问题。
2.选一选。把正确答案的序号填在括号里。 (1)一个三角形中,有一个角是65°,另外的两个角可能是( )。 A.85°,20° B. 45°, 80° C. 55°, 60° (2)一个三角形的三个内角都不小于60° ,这个三角形一定是( )三角形。 A.钝角 B. 直角 C. 等边 (3)用放大5倍的放大镜看一个三角形,这个三角形内角和是( ) A.360° B.900° C. 180° 意图:综合运用三角形内角和、三角形分类解决问题。
3.在点子图上按要求画图。 意图:通过画图形,进一步加深对图形的特征的认识。
拓展性 作业 (选做) 1.直角三角形中,∠A的度数是多少? 意图:综合运用三角形内角和。
2.钝角三角形中已知∠A=140°∠C=25°,求∠B的度数。 意图:综合运用三角形内角和。
3.求出下图中∠1,∠2,∠3的度数。 意图:综合运用三角形内角和。
