六年级下学期数学《圆柱与圆锥》单元分层作业(同步练习)(无答案)北师大版
文档属性
| 名称 | 六年级下学期数学《圆柱与圆锥》单元分层作业(同步练习)(无答案)北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 473.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 12:13:58 | ||
图片预览


文档简介
单元名称 圆柱与圆锥 课题 面的旋转 节次 第一单元第1课时
作业类型 作业内容 设计意图
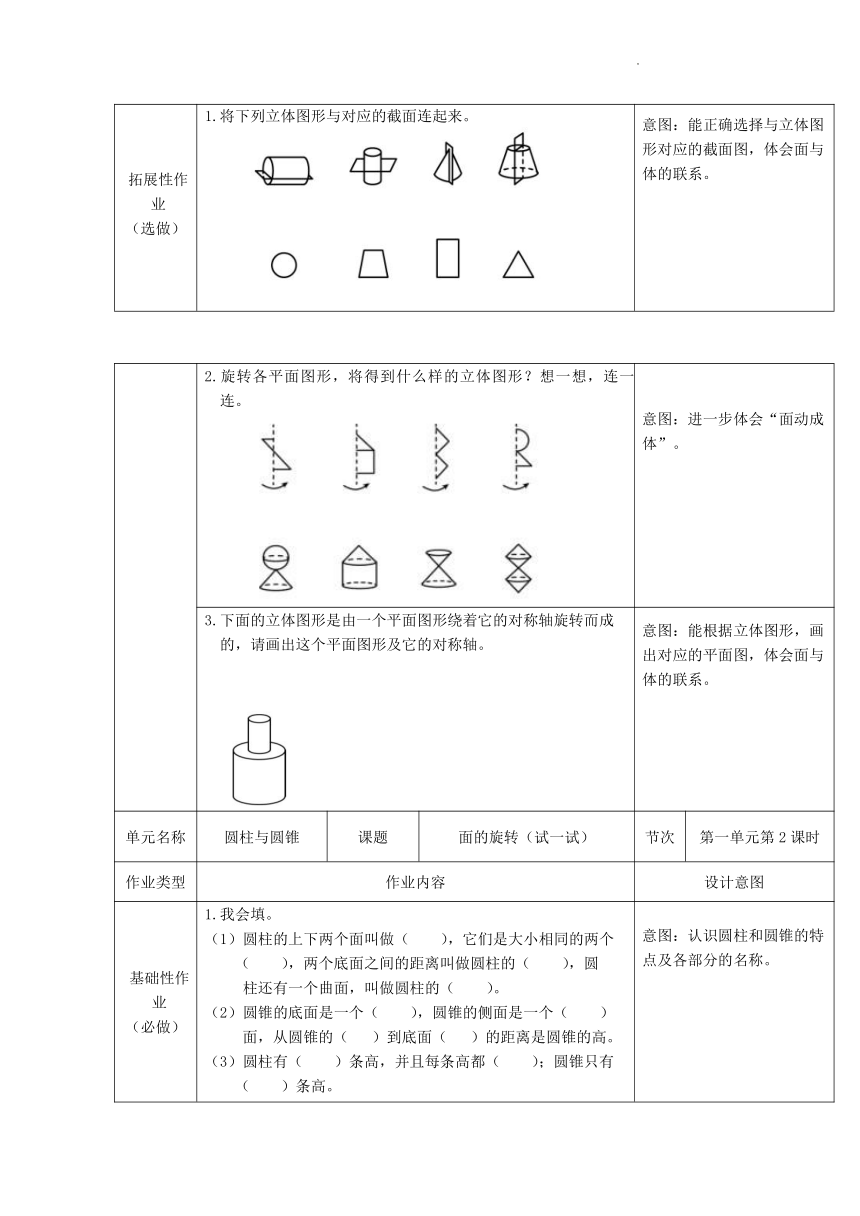
基础性作业 (必做) 1.我会填。 点的运动形成( ),线的运动形成( ),面的运动形成( )。 一个长方形以它的一条边为轴旋转一周,得到一个 ( );直角三角形绕它的一条直角边旋转一周,得到一个( )。 意图:体会“点、线、面、体”之间的联系;通过面的 旋转认识圆柱和圆锥。
2.下列图形绕虚线旋转一周,哪个会形成圆柱?哪个会形成圆锥?用线连一连。 意图:体会“面动成体”, 认识圆柱和圆锥。
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 意图:能正确辨认圆柱和圆锥。
拓展性作业 (选做) 1.将下列立体图形与对应的截面连起来。 意图:能正确选择与立体图形对应的截面图,体会面与体的联系。
2.旋转各平面图形,将得到什么样的立体图形?想一想,连一连。 意图:进一步体会“面动成体”。
3.下面的立体图形是由一个平面图形绕着它的对称轴旋转而成的,请画出这个平面图形及它的对称轴。 意图:能根据立体图形,画出对应的平面图,体会面与体的联系。
单元名称 圆柱与圆锥 课题 面的旋转(试一试) 节次 第一单元第2课时
作业类型 作业内容 设计意图
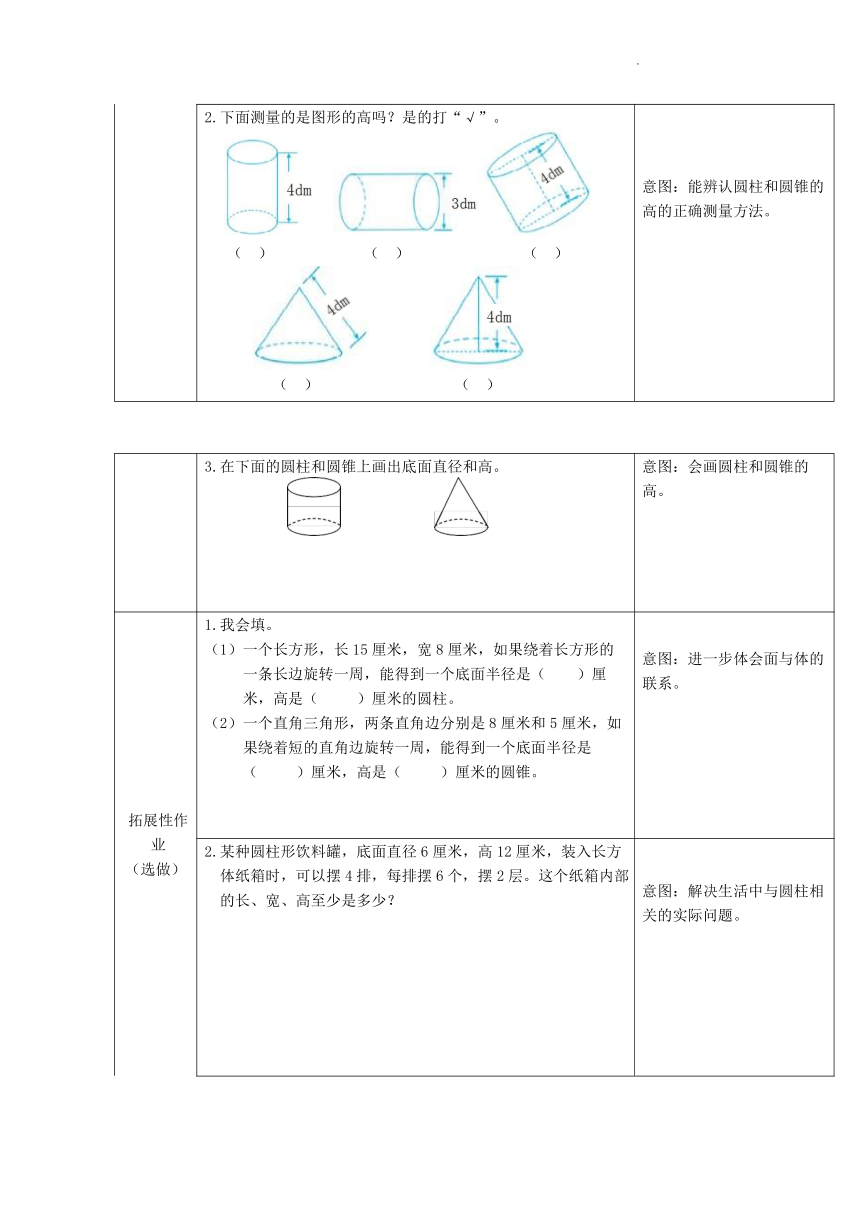
基础性作业 (必做) 1.我会填。 圆柱的上下两个面叫做( ),它们是大小相同的两个 ( ),两个底面之间的距离叫做圆柱的( ),圆 柱还有一个曲面,叫做圆柱的( )。 圆锥的底面是一个( ),圆锥的侧面是一个( ) 面,从圆锥的( )到底面( )的距离是圆锥的高。 圆柱有( )条高,并且每条高都( );圆锥只有 ( )条高。 意图:认识圆柱和圆锥的特 点及各部分的名称。
2.下面测量的是图形的高吗?是的打“√”。 ( ) ( ) ( ) ( ) ( ) 意图:能辨认圆柱和圆锥的 高的正确测量方法。
3.在下面的圆柱和圆锥上画出底面直径和高。 意图:会画圆柱和圆锥的高。
拓展性作业 (选做) 1.我会填。 一个长方形,长15厘米,宽8厘米,如果绕着长方形的一条长边旋转一周,能得到一个底面半径是( )厘米,高是( )厘米的圆柱。 一个直角三角形,两条直角边分别是8厘米和5厘米,如果绕着短的直角边旋转一周,能得到一个底面半径是 ( )厘米,高是( )厘米的圆锥。 意图:进一步体会面与体的联系。
2.某种圆柱形饮料罐,底面直径6厘米,高12厘米,装入长方体纸箱时,可以摆4排,每排摆6个,摆2层。这个纸箱内部的长、宽、高至少是多少? 意图:解决生活中与圆柱相 关的实际问题。
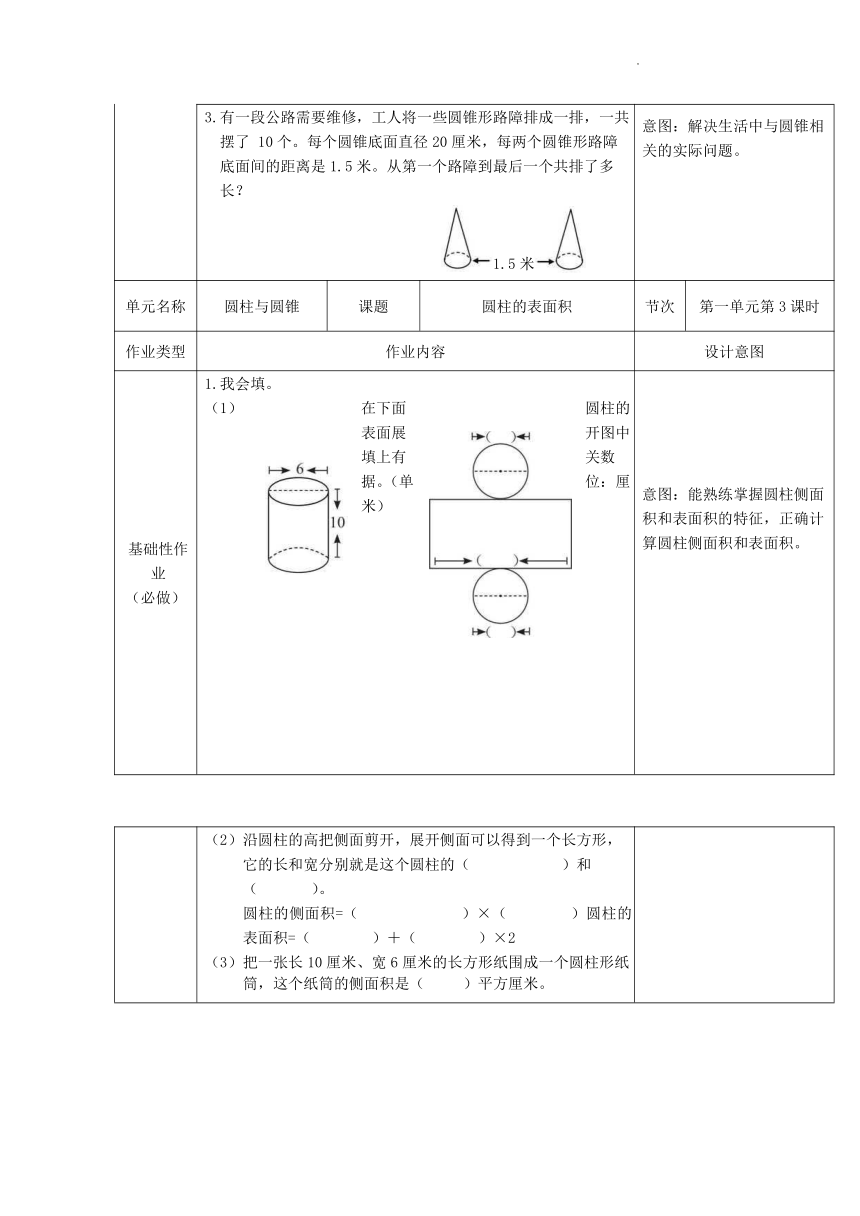
3.有一段公路需要维修,工人将一些圆锥形路障排成一排,一共摆了 10个。每个圆锥底面直径20厘米,每两个圆锥形路障底面间的距离是1.5米。从第一个路障到最后一个共排了多长? 意图:解决生活中与圆锥相 关的实际问题。
单元名称 圆柱与圆锥 课题 圆柱的表面积 节次 第一单元第3课时
作业类型 作业内容 设计意图
基础性作业 (必做) 1.我会填。 (1)在下面圆柱的表面展开图中填上有关数据。(单位:厘米) 意图:能熟练掌握圆柱侧面积和表面积的特征,正确计算圆柱侧面积和表面积。
沿圆柱的高把侧面剪开,展开侧面可以得到一个长方形,它的长和宽分别就是这个圆柱的( )和 ( )。 圆柱的侧面积=( )×( )圆柱的表面积=( )+( )×2 把一张长10厘米、宽6厘米的长方形纸围成一个圆柱形纸筒,这个纸筒的侧面积是( )平方厘米。
2.我会判断。对的画“√”,错的画“×”。 (1)圆柱的侧面积等于底面直径乘高。 ( )(2)沿圆柱的高把侧面剪开,可以得到一个长方形或正方形。 ( ) 把一个圆柱体切成两个小圆柱,表面积比原来增加了两个底面的面积。 ( ) 一个圆柱的底面直径与高相等,它的侧面沿高展开后是一个正方形。 ( ) 如果两个圆柱体的侧面积相等,那么它们的底面周长也一定相等。 ( ) 意图:能根据圆柱侧面积和表面积的相关知识解决实际问题。
3.求圆柱的表面积。 圆柱的底面半径是5分米,高是4分米。 意图:能正确计算圆柱的表面积。
拓展性作业 (选做) 1.我会填。 圆柱的侧面展开图是一个正方形时,圆柱的( )和圆柱的( )相等。 要计算压路机滚动一周能压多大面积的路面,就是求压路机滚筒(圆柱)的( )。 意图:能根据圆柱侧面展开图的知识解决实际问题。
2.求圆柱的表面积。 圆柱的底面直径是8厘米,高是直径的1.5倍。 意图:能正确计算圆柱的表面积。
3.下面哪个是圆柱的表面展开图?说说你是如何判定的。 意图:能正确辨认圆柱的表面展开图。
单元名称 圆柱与圆锥 课题 圆柱的表面积(试一试) 节次 第一单元第4课时
作业类型 作业内容 设计意图
基础性作业 (必做) 1.右图是一个用铝皮做成的饮料罐。(单位:厘米) 这个饮料罐的底面积是多少平方厘米? 要在饮料罐的侧面贴满一圈包装纸,至少需要多大面积的包装纸? 做一个这样的饮料罐,至少需要多少平方厘米的铝皮? 意图:能运用圆柱表面积的计算方法解决实际问题。
2.一个圆柱的底面周长是12.56厘米,高是3厘米,这个圆柱的表面积是多少平方厘米? 意图:能正确计算圆柱的表面积。
3.一个无盖的圆柱形水桶,高是60厘米,底面半径是20厘米,将水桶的外表面涂漆,涂漆的面积是多少平方厘米? 意图:能运用圆柱表面积的计算方法解决实际问题。
拓展性作业 (选做) 1.一个圆柱形通风管的底面直径是20厘米,长是40厘米。做 20根这样的通风管,至少要用多少平方厘米的铁皮? 意图:能运用圆柱侧面积的计算方法解决实际问题。
2.一个圆柱形的饼干盒,它的侧面展开后是一个正方形,已知饼干盒的底面周长是25.12厘米,这个饼干盒的表面积是多少平方厘米? 意图:能正确计算圆柱的表面积。
3.如果用下图中的长方形纸作侧面围成一个圆柱,请你选择合适的圆作底面。 直径4.5cm 直径5cm 直径6cm 意图:能根据圆柱侧面展开 图选择合适的底面。
单元名称 圆柱与圆锥 课题 圆柱的体积 节次 第一单元第5课时
作业类型 作业内容 设计意图
基础性作业 (必做) 1.我会填。 如图所示,将圆柱切拼成一个近似长方体。 长方体的底面近似一个( )形,它的长等于圆柱的 ( )的一半,它的宽等于圆柱的( )。 长方体的底面积等于圆柱的( ),长方体的高等于圆柱的( ), 由于在切拼的过程中体积保持不变,所以: 圆柱的体积=长方体的体积=( )×( )。 一个圆柱按上图方法切拼成的长方体底面的宽是3厘米,高8厘米,这个圆柱的体积是( )立方厘米。 意图:理解、掌握圆柱体积的计算方法。
2.填表。 意图:读懂表格,能根据圆柱体积计算公式正确计算。
底面积/平方米 高/米 圆柱的体积/立方米
3.96 4
4 9.6
5 2.55
3.计算下面各圆柱的体积。(单位:厘米) 意图:能正确计算圆柱的体积。
拓展性作业 (选做) 1.我会填。 一个圆柱体的底面积是105平方分米,高是4分米,体积是( )立方分米。 一根长2米的圆木,截成两段小圆柱后,表面积增加48 平方厘米,这根圆木原来的体积是( )立方厘米。 意图:能运用圆柱体积计算方法解决简单的实际问题。
2.下面哪个杯子里的水最多?算一算。(单位:cm) 意图:能运用圆柱体积计算 方法计算杯子的容积。
3.算一算,这个杯子能不能装下这袋牛奶。 意图:能运用圆柱体积计算方法解决简单的实际问题。
单元名称 圆柱与圆锥 课题 圆柱的体积(试一试) 节次 第一单元第6课时
作业类型 作业内容 设计意图
基础性作业 (必做) 1.我会判断。 长方体、正方体、圆柱体的体积都可以用“V=Sh”来计 算。 ( ) 圆柱的底面半径和高都扩大到原来的2倍,它的体积扩大 到原来的4倍。 ( ) 意图:能运用圆柱体积计算方法解决简单的实际问题。
2.我会选择。 把一个棱长是4分米的正方体木块切削成一个最大的圆柱,这个圆柱的体积是( )立方分米。 A.50.24 B. 64 C. 12.56 D. 200.96 体积单位和面积单位相比较,( )。 A.体积单位大 B.面积单位大 C.一样大 D.无法比较 等底等高的圆柱体、正方体、长方体的体积相比较, ( )。 A.正方体体积大 B.长方体体积大 C.圆柱体体积大 D.一样大 意图:能运用圆柱体积的相 关知识解决简单的实际问题。
(4)正方体的表面积是6平方厘米,它的体积是( )立方厘米。 A.6 B. 4 C. 1 D. 5
3.一个圆柱的体积是150.72立方厘米,底面周长是12.56厘米,它的高是多少厘米? 意图:能运用圆柱体积计算方法解决简单的实际问题。
拓展性作业 (选做) 1.一根圆柱形木料的底面直径是4分米,长3米。它的表面积是多少平方分米?它的体积是多少立方分米? 意图:能正确计算圆柱的表面积和体积。
2.一个底面积是125.6平方米的圆柱形蓄水池,容积是314立方米。如果再深挖0.5米,水池容积是多少立方米? 意图:能运用圆柱体积计算方法解决简单的实际问题。
3.在乌鸦喝水的故事中,聪明的乌鸦为了能喝到水,就把小石子放入水瓶中。 如果这个瓶子是个圆柱形,它的底面半径是 4厘米,放入石子后(石子完全浸没水中)水面上升了5厘米。同学们,你们能计算出放入石子的体积吗? 意图:能运用圆柱体积计算方法解决简单的实际问题。
单元名称 圆柱与圆锥 课题 圆锥的体积 节次 第一单元第7课时
作业类型 作业内容 设计意图
基础性作业 (必做) 1.我会填。 一个圆柱和一个圆锥的底面积和高分别相等,圆锥的体积是圆柱体积的( ),圆柱的体积是圆锥体积的 ( )倍。 圆锥的底面半径是6厘米,高是20厘米,它的体积是 ( )厘米。 把一个圆柱削成最大的圆锥,若圆锥体积是72立方厘米, 就要削去( )立方厘米。 一个圆柱体和一个圆锥体的底面积和体积分别相等,已知 圆柱体的高是6厘米,那么圆锥体的高是( )厘米。 意图:理解等底等高的圆柱和圆锥体积之间的联系,掌握圆锥体积的计算方法。
2.我会判断。 圆锥的体积是圆柱体积的 。 ( ) 有一个圆柱体和一个圆锥体,它们的底面半径相等,高也相等,圆柱的体积是6立方分米,则圆锥的体积是2立方分米。 ( ) 一个圆锥体的底面积扩大到原来的6倍,高不变,这个圆锥的体积也扩大到原来的6倍。 ( ) 一个正方体和一个圆锥体的底面积和高分别相等,则这个正方体体积是圆锥体积的3倍。 ( ) 意图:能运用圆锥体积计算方法解决简单的实际问题。
3.求圆锥的体积。 底面半径是3厘米,高是5厘米。 底面周长是12.56分米,高是6分米。 意图:能正确计算圆锥的体积。
拓展性作业 (选做) 1.下图是两个等底等高的圆柱和圆锥。如果圆柱与圆锥的体积之和是62.4分米 3,求圆柱与圆锥的体积。 意图:能运用等底等高的圆柱和圆锥体积之间的联系解决简单的实际问题。
2.沙漏是我国古代一种计时工具,如图所示(单位:分米)。现在沙漏已经装满了沙,如果每小时流出8升沙,那么沙漏里的沙全部流出需要多少小时? 意图:能运用圆锥体积计算方法解决简单的实际问题。
3.我会解决问题。 如图所示,有甲、乙两个容器(单位:厘米),先将甲容器注满水,然后将水倒入乙容器,求乙容器的水深。 意图:能运用圆柱和圆锥体积计算公式解决简单的实际问题。
单元名称 圆柱与圆锥 课题 练习一 节次 第一单元第8课时
作业类型 作业内容 设计意图
基础性作业 (必做) 1.我会填。 一根底面直径是20厘米、高2米的圆柱形铁皮通风管,沿着高剪开得到一个长方形,它的长是( )米,宽是 ( )米。 一个圆柱的侧面积是25.12平方分米,底面直径是4分米,它的高是( )分米。 一根圆柱形铁棒,底面半径是2厘米,长是100厘米,它的体积是( )立方厘米。 把一个体积是18立方厘米的圆柱削成一个最大的圆锥,削成的圆锥体积是( )立方厘米。 意图:能运用圆柱和圆锥的相关知识解决实际问题。
2.我会判断。 圆柱的侧面展开图不可能是平行四边形。 ( ) 一段圆柱形木料,削成一个最大的圆锥,削去的体积是削成的圆锥体积的2倍。 ( ) 直角三角形绕一条边旋转后形成的立体图形一定是圆锥。 ( ) 一个圆柱和一个圆锥的体积和底面积分别相等,圆锥的高是9厘米,则圆柱的高是3厘米。 ( ) 意图:能运用圆柱和圆锥的相关知识解决实际问题
3.我会解决问题。 工地上有一个圆锥形沙堆,它的底面周长是12.56米,高是1.5米。把这些沙子铺在长4米、宽2米的长方体沙坑内,可以铺多厚? 一个直角三角形的两条直角边分别是10厘米和9厘米,以10厘米长的直角边为轴旋转一周,所得到的图形的体积是多少? 下图是一块长方形铁皮,利用图中的阴影部分,刚好能做成一个油桶(接头处忽略不计),求这个油桶的容积。 (单位:分米) 意图:能运用圆柱和圆锥的相关知识解决实际问题。
拓展性作业 (选做) 1.我会填。 一个圆柱和一个圆锥等底等高,圆锥的体积比圆柱的体积少0.8立方分米,那么圆锥的体积是( )立方分米,圆柱的体积是( )立方分米。 一个圆柱的底面半径是8厘米,高是15厘米,它的表面积是( )平方厘米。 把一个圆柱形钢材横截成3段小圆柱,增加了( )个底面。 意图:能运用圆柱和圆锥的相关知识解决实际问题。
2.我会选。 一个圆锥的底面半径扩大到原来的3倍,高不变,它的体积扩大到原来的( )倍。 3 B. 6 C. 9 在一个高15厘米的圆锥形容器中盛满水,再把水倒入它等底等高的圆柱形容器中,圆柱形容器内水的高度是 ( )厘米。 5 B. 10 C. 15 把一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是( )立方分米。 50.24 B. 100.48 C. 64 意图:能运用圆柱和圆锥的相关知识解决实际问题。
3.我会解决问题。 一台压路机的前轮是圆柱形,轮宽2米,直径1.2米。前轮转动一周,压路的面积是多少平方米? 用塑料绳捆扎一个圆柱形的蛋糕盒(如下图所示,单位:厘米),打结处正好是底面圆心,打结用去绳长25厘米。 ①扎这个盒子至少用去塑料绳多少厘米? ②在它的侧面贴满一圈商标纸,至少需要多少平方厘米商标纸? 意图:能运用圆柱和圆锥的相关知识解决实际问题。
作业类型 作业内容 设计意图
基础性作业 (必做) 1.我会填。 点的运动形成( ),线的运动形成( ),面的运动形成( )。 一个长方形以它的一条边为轴旋转一周,得到一个 ( );直角三角形绕它的一条直角边旋转一周,得到一个( )。 意图:体会“点、线、面、体”之间的联系;通过面的 旋转认识圆柱和圆锥。
2.下列图形绕虚线旋转一周,哪个会形成圆柱?哪个会形成圆锥?用线连一连。 意图:体会“面动成体”, 认识圆柱和圆锥。
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 意图:能正确辨认圆柱和圆锥。
拓展性作业 (选做) 1.将下列立体图形与对应的截面连起来。 意图:能正确选择与立体图形对应的截面图,体会面与体的联系。
2.旋转各平面图形,将得到什么样的立体图形?想一想,连一连。 意图:进一步体会“面动成体”。
3.下面的立体图形是由一个平面图形绕着它的对称轴旋转而成的,请画出这个平面图形及它的对称轴。 意图:能根据立体图形,画出对应的平面图,体会面与体的联系。
单元名称 圆柱与圆锥 课题 面的旋转(试一试) 节次 第一单元第2课时
作业类型 作业内容 设计意图
基础性作业 (必做) 1.我会填。 圆柱的上下两个面叫做( ),它们是大小相同的两个 ( ),两个底面之间的距离叫做圆柱的( ),圆 柱还有一个曲面,叫做圆柱的( )。 圆锥的底面是一个( ),圆锥的侧面是一个( ) 面,从圆锥的( )到底面( )的距离是圆锥的高。 圆柱有( )条高,并且每条高都( );圆锥只有 ( )条高。 意图:认识圆柱和圆锥的特 点及各部分的名称。
2.下面测量的是图形的高吗?是的打“√”。 ( ) ( ) ( ) ( ) ( ) 意图:能辨认圆柱和圆锥的 高的正确测量方法。
3.在下面的圆柱和圆锥上画出底面直径和高。 意图:会画圆柱和圆锥的高。
拓展性作业 (选做) 1.我会填。 一个长方形,长15厘米,宽8厘米,如果绕着长方形的一条长边旋转一周,能得到一个底面半径是( )厘米,高是( )厘米的圆柱。 一个直角三角形,两条直角边分别是8厘米和5厘米,如果绕着短的直角边旋转一周,能得到一个底面半径是 ( )厘米,高是( )厘米的圆锥。 意图:进一步体会面与体的联系。
2.某种圆柱形饮料罐,底面直径6厘米,高12厘米,装入长方体纸箱时,可以摆4排,每排摆6个,摆2层。这个纸箱内部的长、宽、高至少是多少? 意图:解决生活中与圆柱相 关的实际问题。
3.有一段公路需要维修,工人将一些圆锥形路障排成一排,一共摆了 10个。每个圆锥底面直径20厘米,每两个圆锥形路障底面间的距离是1.5米。从第一个路障到最后一个共排了多长? 意图:解决生活中与圆锥相 关的实际问题。
单元名称 圆柱与圆锥 课题 圆柱的表面积 节次 第一单元第3课时
作业类型 作业内容 设计意图
基础性作业 (必做) 1.我会填。 (1)在下面圆柱的表面展开图中填上有关数据。(单位:厘米) 意图:能熟练掌握圆柱侧面积和表面积的特征,正确计算圆柱侧面积和表面积。
沿圆柱的高把侧面剪开,展开侧面可以得到一个长方形,它的长和宽分别就是这个圆柱的( )和 ( )。 圆柱的侧面积=( )×( )圆柱的表面积=( )+( )×2 把一张长10厘米、宽6厘米的长方形纸围成一个圆柱形纸筒,这个纸筒的侧面积是( )平方厘米。
2.我会判断。对的画“√”,错的画“×”。 (1)圆柱的侧面积等于底面直径乘高。 ( )(2)沿圆柱的高把侧面剪开,可以得到一个长方形或正方形。 ( ) 把一个圆柱体切成两个小圆柱,表面积比原来增加了两个底面的面积。 ( ) 一个圆柱的底面直径与高相等,它的侧面沿高展开后是一个正方形。 ( ) 如果两个圆柱体的侧面积相等,那么它们的底面周长也一定相等。 ( ) 意图:能根据圆柱侧面积和表面积的相关知识解决实际问题。
3.求圆柱的表面积。 圆柱的底面半径是5分米,高是4分米。 意图:能正确计算圆柱的表面积。
拓展性作业 (选做) 1.我会填。 圆柱的侧面展开图是一个正方形时,圆柱的( )和圆柱的( )相等。 要计算压路机滚动一周能压多大面积的路面,就是求压路机滚筒(圆柱)的( )。 意图:能根据圆柱侧面展开图的知识解决实际问题。
2.求圆柱的表面积。 圆柱的底面直径是8厘米,高是直径的1.5倍。 意图:能正确计算圆柱的表面积。
3.下面哪个是圆柱的表面展开图?说说你是如何判定的。 意图:能正确辨认圆柱的表面展开图。
单元名称 圆柱与圆锥 课题 圆柱的表面积(试一试) 节次 第一单元第4课时
作业类型 作业内容 设计意图
基础性作业 (必做) 1.右图是一个用铝皮做成的饮料罐。(单位:厘米) 这个饮料罐的底面积是多少平方厘米? 要在饮料罐的侧面贴满一圈包装纸,至少需要多大面积的包装纸? 做一个这样的饮料罐,至少需要多少平方厘米的铝皮? 意图:能运用圆柱表面积的计算方法解决实际问题。
2.一个圆柱的底面周长是12.56厘米,高是3厘米,这个圆柱的表面积是多少平方厘米? 意图:能正确计算圆柱的表面积。
3.一个无盖的圆柱形水桶,高是60厘米,底面半径是20厘米,将水桶的外表面涂漆,涂漆的面积是多少平方厘米? 意图:能运用圆柱表面积的计算方法解决实际问题。
拓展性作业 (选做) 1.一个圆柱形通风管的底面直径是20厘米,长是40厘米。做 20根这样的通风管,至少要用多少平方厘米的铁皮? 意图:能运用圆柱侧面积的计算方法解决实际问题。
2.一个圆柱形的饼干盒,它的侧面展开后是一个正方形,已知饼干盒的底面周长是25.12厘米,这个饼干盒的表面积是多少平方厘米? 意图:能正确计算圆柱的表面积。
3.如果用下图中的长方形纸作侧面围成一个圆柱,请你选择合适的圆作底面。 直径4.5cm 直径5cm 直径6cm 意图:能根据圆柱侧面展开 图选择合适的底面。
单元名称 圆柱与圆锥 课题 圆柱的体积 节次 第一单元第5课时
作业类型 作业内容 设计意图
基础性作业 (必做) 1.我会填。 如图所示,将圆柱切拼成一个近似长方体。 长方体的底面近似一个( )形,它的长等于圆柱的 ( )的一半,它的宽等于圆柱的( )。 长方体的底面积等于圆柱的( ),长方体的高等于圆柱的( ), 由于在切拼的过程中体积保持不变,所以: 圆柱的体积=长方体的体积=( )×( )。 一个圆柱按上图方法切拼成的长方体底面的宽是3厘米,高8厘米,这个圆柱的体积是( )立方厘米。 意图:理解、掌握圆柱体积的计算方法。
2.填表。 意图:读懂表格,能根据圆柱体积计算公式正确计算。
底面积/平方米 高/米 圆柱的体积/立方米
3.96 4
4 9.6
5 2.55
3.计算下面各圆柱的体积。(单位:厘米) 意图:能正确计算圆柱的体积。
拓展性作业 (选做) 1.我会填。 一个圆柱体的底面积是105平方分米,高是4分米,体积是( )立方分米。 一根长2米的圆木,截成两段小圆柱后,表面积增加48 平方厘米,这根圆木原来的体积是( )立方厘米。 意图:能运用圆柱体积计算方法解决简单的实际问题。
2.下面哪个杯子里的水最多?算一算。(单位:cm) 意图:能运用圆柱体积计算 方法计算杯子的容积。
3.算一算,这个杯子能不能装下这袋牛奶。 意图:能运用圆柱体积计算方法解决简单的实际问题。
单元名称 圆柱与圆锥 课题 圆柱的体积(试一试) 节次 第一单元第6课时
作业类型 作业内容 设计意图
基础性作业 (必做) 1.我会判断。 长方体、正方体、圆柱体的体积都可以用“V=Sh”来计 算。 ( ) 圆柱的底面半径和高都扩大到原来的2倍,它的体积扩大 到原来的4倍。 ( ) 意图:能运用圆柱体积计算方法解决简单的实际问题。
2.我会选择。 把一个棱长是4分米的正方体木块切削成一个最大的圆柱,这个圆柱的体积是( )立方分米。 A.50.24 B. 64 C. 12.56 D. 200.96 体积单位和面积单位相比较,( )。 A.体积单位大 B.面积单位大 C.一样大 D.无法比较 等底等高的圆柱体、正方体、长方体的体积相比较, ( )。 A.正方体体积大 B.长方体体积大 C.圆柱体体积大 D.一样大 意图:能运用圆柱体积的相 关知识解决简单的实际问题。
(4)正方体的表面积是6平方厘米,它的体积是( )立方厘米。 A.6 B. 4 C. 1 D. 5
3.一个圆柱的体积是150.72立方厘米,底面周长是12.56厘米,它的高是多少厘米? 意图:能运用圆柱体积计算方法解决简单的实际问题。
拓展性作业 (选做) 1.一根圆柱形木料的底面直径是4分米,长3米。它的表面积是多少平方分米?它的体积是多少立方分米? 意图:能正确计算圆柱的表面积和体积。
2.一个底面积是125.6平方米的圆柱形蓄水池,容积是314立方米。如果再深挖0.5米,水池容积是多少立方米? 意图:能运用圆柱体积计算方法解决简单的实际问题。
3.在乌鸦喝水的故事中,聪明的乌鸦为了能喝到水,就把小石子放入水瓶中。 如果这个瓶子是个圆柱形,它的底面半径是 4厘米,放入石子后(石子完全浸没水中)水面上升了5厘米。同学们,你们能计算出放入石子的体积吗? 意图:能运用圆柱体积计算方法解决简单的实际问题。
单元名称 圆柱与圆锥 课题 圆锥的体积 节次 第一单元第7课时
作业类型 作业内容 设计意图
基础性作业 (必做) 1.我会填。 一个圆柱和一个圆锥的底面积和高分别相等,圆锥的体积是圆柱体积的( ),圆柱的体积是圆锥体积的 ( )倍。 圆锥的底面半径是6厘米,高是20厘米,它的体积是 ( )厘米。 把一个圆柱削成最大的圆锥,若圆锥体积是72立方厘米, 就要削去( )立方厘米。 一个圆柱体和一个圆锥体的底面积和体积分别相等,已知 圆柱体的高是6厘米,那么圆锥体的高是( )厘米。 意图:理解等底等高的圆柱和圆锥体积之间的联系,掌握圆锥体积的计算方法。
2.我会判断。 圆锥的体积是圆柱体积的 。 ( ) 有一个圆柱体和一个圆锥体,它们的底面半径相等,高也相等,圆柱的体积是6立方分米,则圆锥的体积是2立方分米。 ( ) 一个圆锥体的底面积扩大到原来的6倍,高不变,这个圆锥的体积也扩大到原来的6倍。 ( ) 一个正方体和一个圆锥体的底面积和高分别相等,则这个正方体体积是圆锥体积的3倍。 ( ) 意图:能运用圆锥体积计算方法解决简单的实际问题。
3.求圆锥的体积。 底面半径是3厘米,高是5厘米。 底面周长是12.56分米,高是6分米。 意图:能正确计算圆锥的体积。
拓展性作业 (选做) 1.下图是两个等底等高的圆柱和圆锥。如果圆柱与圆锥的体积之和是62.4分米 3,求圆柱与圆锥的体积。 意图:能运用等底等高的圆柱和圆锥体积之间的联系解决简单的实际问题。
2.沙漏是我国古代一种计时工具,如图所示(单位:分米)。现在沙漏已经装满了沙,如果每小时流出8升沙,那么沙漏里的沙全部流出需要多少小时? 意图:能运用圆锥体积计算方法解决简单的实际问题。
3.我会解决问题。 如图所示,有甲、乙两个容器(单位:厘米),先将甲容器注满水,然后将水倒入乙容器,求乙容器的水深。 意图:能运用圆柱和圆锥体积计算公式解决简单的实际问题。
单元名称 圆柱与圆锥 课题 练习一 节次 第一单元第8课时
作业类型 作业内容 设计意图
基础性作业 (必做) 1.我会填。 一根底面直径是20厘米、高2米的圆柱形铁皮通风管,沿着高剪开得到一个长方形,它的长是( )米,宽是 ( )米。 一个圆柱的侧面积是25.12平方分米,底面直径是4分米,它的高是( )分米。 一根圆柱形铁棒,底面半径是2厘米,长是100厘米,它的体积是( )立方厘米。 把一个体积是18立方厘米的圆柱削成一个最大的圆锥,削成的圆锥体积是( )立方厘米。 意图:能运用圆柱和圆锥的相关知识解决实际问题。
2.我会判断。 圆柱的侧面展开图不可能是平行四边形。 ( ) 一段圆柱形木料,削成一个最大的圆锥,削去的体积是削成的圆锥体积的2倍。 ( ) 直角三角形绕一条边旋转后形成的立体图形一定是圆锥。 ( ) 一个圆柱和一个圆锥的体积和底面积分别相等,圆锥的高是9厘米,则圆柱的高是3厘米。 ( ) 意图:能运用圆柱和圆锥的相关知识解决实际问题
3.我会解决问题。 工地上有一个圆锥形沙堆,它的底面周长是12.56米,高是1.5米。把这些沙子铺在长4米、宽2米的长方体沙坑内,可以铺多厚? 一个直角三角形的两条直角边分别是10厘米和9厘米,以10厘米长的直角边为轴旋转一周,所得到的图形的体积是多少? 下图是一块长方形铁皮,利用图中的阴影部分,刚好能做成一个油桶(接头处忽略不计),求这个油桶的容积。 (单位:分米) 意图:能运用圆柱和圆锥的相关知识解决实际问题。
拓展性作业 (选做) 1.我会填。 一个圆柱和一个圆锥等底等高,圆锥的体积比圆柱的体积少0.8立方分米,那么圆锥的体积是( )立方分米,圆柱的体积是( )立方分米。 一个圆柱的底面半径是8厘米,高是15厘米,它的表面积是( )平方厘米。 把一个圆柱形钢材横截成3段小圆柱,增加了( )个底面。 意图:能运用圆柱和圆锥的相关知识解决实际问题。
2.我会选。 一个圆锥的底面半径扩大到原来的3倍,高不变,它的体积扩大到原来的( )倍。 3 B. 6 C. 9 在一个高15厘米的圆锥形容器中盛满水,再把水倒入它等底等高的圆柱形容器中,圆柱形容器内水的高度是 ( )厘米。 5 B. 10 C. 15 把一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是( )立方分米。 50.24 B. 100.48 C. 64 意图:能运用圆柱和圆锥的相关知识解决实际问题。
3.我会解决问题。 一台压路机的前轮是圆柱形,轮宽2米,直径1.2米。前轮转动一周,压路的面积是多少平方米? 用塑料绳捆扎一个圆柱形的蛋糕盒(如下图所示,单位:厘米),打结处正好是底面圆心,打结用去绳长25厘米。 ①扎这个盒子至少用去塑料绳多少厘米? ②在它的侧面贴满一圈商标纸,至少需要多少平方厘米商标纸? 意图:能运用圆柱和圆锥的相关知识解决实际问题。
