2013年高考模拟系列试卷(2)【新课标版】(理)
文档属性
| 名称 | 2013年高考模拟系列试卷(2)【新课标版】(理) |  | |
| 格式 | zip | ||
| 文件大小 | 272.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-15 16:48:45 | ||
图片预览



文档简介
2013年高考模拟系列试卷(二)
数学试题【新课标版】(理科)
题 号
第Ⅰ卷
第Ⅱ卷
总分
一
二
17
18
19
20
21
22
得 分
注意事项:
1.本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题,共60分)
一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的
1、设集合,,则等于 ( )
A.R B. C. D.
2、在复平面内,复数表示的点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3、若,则( )
A. B. C. D.
4、设数列是公差不为零的等差数列,它的前项和为,且、、成等比数列,则等于( )
A.6 B.7 C.4 D.3
5、已知点和圆上一动点,动点满足,则点的轨迹方程是( )
A.B.C. D.
6、命题“存在,使”的否定为( )
A.任意,使
B.任意,使
C.存在,使
D.存在,使
7、设,函数的图象可能是( )
8、程序框图如下:
如果上述程序运行的结果S的值比2013小,若使输出的S最大,那么判断框中应填入( )
A. B. C. D.
9、图为一个空间几何体的三视图,其中俯视图是下边一个等边三角形,其内切圆的半径是1,正视图和侧视图是上边两个图形,数据如图,则此几何体的体积是( )
A. B. C. D.
10、在的展开式中,常数项为( )
A. B.5376 C. D.84
11、如果点P在平面区域上,点Q在曲线(x-1)2+(y-1)2=1上,那么|PQ|的最小值为( )
A.-1 B. C. D.-1
12、已知椭圆C:的左右焦点为,过的直线与圆相切于点A,并与椭圆C交与不同的两点P,Q,如图,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为 ( )
A. B. C. D.
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上
13、由曲线和直线所围成的面积为 。
14、如图,△ABC是圆内接三角形,圆心O在BC上,若AB=6,BD=3.6,将一颗豆子随机地扔到该圆内,用M表示事件“豆子落在△ABC内”,N表示事件“豆子落在△ABD内”,则P(N|M)= .
15、某市居民用户12月份燃气用量(单位:m3)的频率分布直方图如图所示,现抽取了500户进行调查,则用气量在[26,36)的户数为 。
16、在△ABC中,D为AB上任一点,h为AB边上的高,△ADC、△BDC、△ABC的内切圆半径分别为,则有如下的等式恒成立:.在三棱锥P-ABC中D位AB上任一点,h为过点P的三棱锥的高,三棱锥P-ADC、P-BDC、P-ABC的内切球的半径分别为,请类比平面三角形中的结论,写出类似的一个恒等式为 .
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤
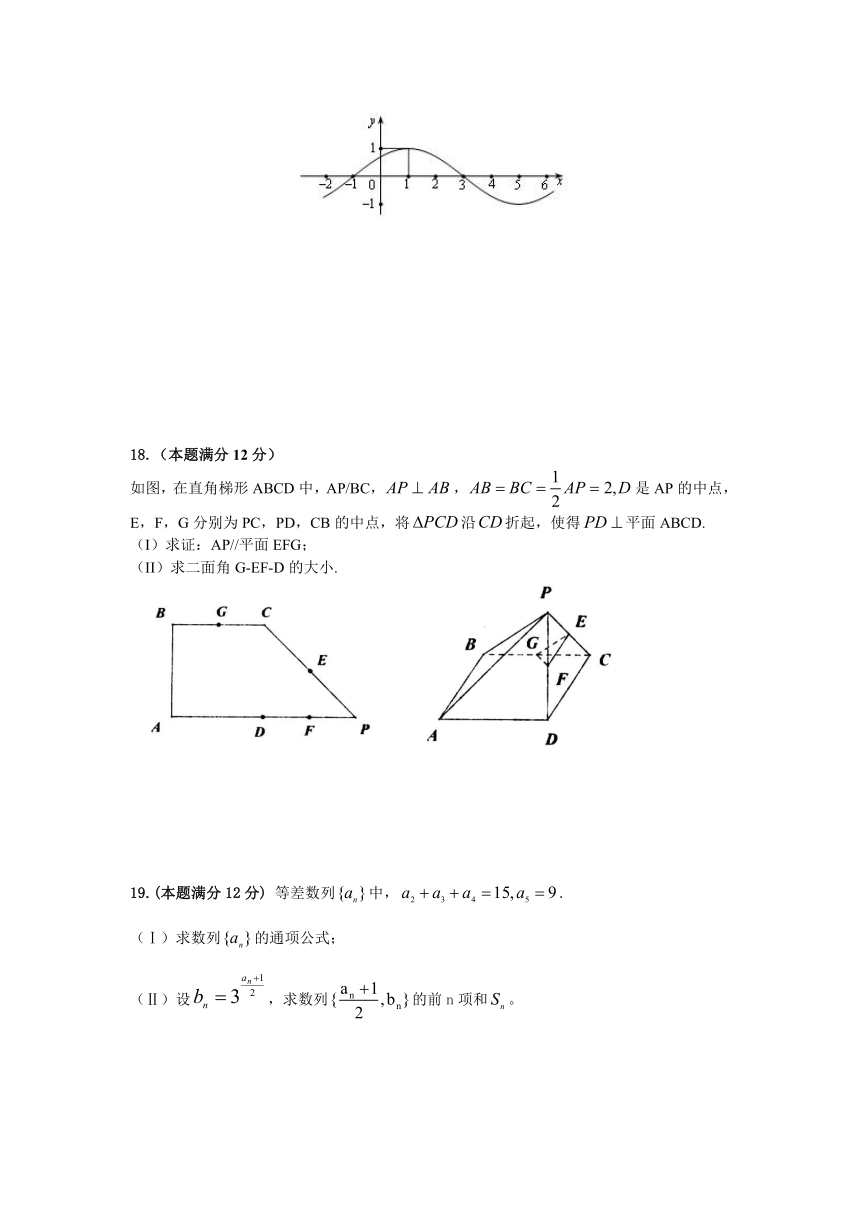
17.(本题满分12分)已知函数,(其中),其部分图像如图所示.
(I)求函数的解析式;
(Ⅱ)已知横坐标分别为、、的三点、、都在函数的图像上,求的值.
18.(本题满分12分)
如图,在直角梯形ABCD中,AP/BC,,是AP的中点,E,F,G分别为PC,PD,CB的中点,将沿折起,使得平面ABCD.
(I)求证:AP//平面EFG;
(II)求二面角G-EF-D的大小.
19.(本题满分12分) 等差数列中,.
(Ⅰ)求数列的通项公式;
(Ⅱ)设,求数列的前n项和。
20.(本小题满分12分)
若盒中装有同一型号的灯泡共10只,其中有8只合格品,2只次品。
某工人师傅有放回地连续从该盒中取灯泡3次,每次取一只灯泡,求2次取到次品的概率;
(Ⅱ)某工人师傅有该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡所用灯泡只数的分布列和数学期望。
21.(本题满分13分)已知函数,.
(I)若函数,求函数的单调区间;
(Ⅱ)设直线为函数的图象上一点处的切线.证明:在区间上存在唯一的,使得直线l与曲线相切.
22.(本题满分13分)
已知椭圆过点,其长轴、焦距和短轴的长的平方依次成等差数列.直线与轴正半轴和轴分别交于点、,与椭圆分别交于点、,各点均不重合且满足
(I)求椭圆的标准方程;
(Ⅱ)若,试证明:直线过定点并求此定点.
参考答案
一选择题(每题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
A
B
C
B
B
C
B
A
C
C
二填空题(每题4分,满分16分,将答案填在答题纸上)
13. 14. 15. 16.
三解答题
17.【解析】(Ⅰ)由图可知, 最小正周期 所以.
又 ,且,
所以,.所以.
(Ⅱ)解法一:因为
所以,,
从而.
由得.
解法二:因为,
,所以,
,
,
则.
由得.
18.【解析】 (Ⅰ) 证明: 由题知,直线两两垂直,以为原点,以
为方向向量建立空间直角坐标系,如图所示.
则.
所以 . ……2分
设平面的法向量为,
取. ……………………4分
∵,
又平面,
//平面. ……………………6分
(Ⅱ)由已知底面ABCD是正方形,.又∵面ABCD,
.又,
平面PCD,向量是平面PCD的一个法向量, = . ……9分
又由(Ⅰ)知平面EFG的法向量为,
结合图知二面角的平面角为 ……………………12分
19.【解析】(Ⅰ)设数列
且,解得………2分
所以数列……4分
(Ⅱ)由(Ⅰ)可得,所以………6分
所以………
两式相减得……………10 分
…………12分
20.【解析】设一次取次品记为事件A,由古典概型概率公式得:……2 分
有放回连续取3次,其中2次取得次品记为事件B,由独立重复试验得:………4分
(2)依据知X的可能取值为1.2.3………5
且………6 ………7
………8
则X的分布列如下表:
X
1
2
3
p
……10分
………12分
21.【解析】(Ⅰ),.
∵且,∴,∴函数的单调递增区间为.
(Ⅱ)∵,∴,∴切线的方程为,
即, ①
设直线与曲线相切于点,∵,∴,∴.∴直线也为, 即, ②
由①②得,∴.
下证:在区间(1,+)上存在且唯一.
由(1)可知,在区间上递增.
又,,
结合零点存在性定理,说明方程必在区间上有唯一的根,这个根就是所求的唯一.故结论成立.
22.【解析】(Ⅰ)设椭圆方程为,焦距为2c, -------1分
由题意知 b=1,且,又
得. -------------3分
所以椭圆的方程为 ---------5分
(Ⅱ) 由题意设,设l方程为,
由知
∴,由题意,∴ -----------------7分
同理由知
∵,∴ (*) ------8分
联立得
∴需 (**)
且有 (***) -------10分
(***)代入(*)得,∴,
由题意,∴(满足(**)), ----------12分
得l方程为,过定点(1,0),即P为定点. ---------------13分
数学试题【新课标版】(理科)
题 号
第Ⅰ卷
第Ⅱ卷
总分
一
二
17
18
19
20
21
22
得 分
注意事项:
1.本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题,共60分)
一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的
1、设集合,,则等于 ( )
A.R B. C. D.
2、在复平面内,复数表示的点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3、若,则( )
A. B. C. D.
4、设数列是公差不为零的等差数列,它的前项和为,且、、成等比数列,则等于( )
A.6 B.7 C.4 D.3
5、已知点和圆上一动点,动点满足,则点的轨迹方程是( )
A.B.C. D.
6、命题“存在,使”的否定为( )
A.任意,使
B.任意,使
C.存在,使
D.存在,使
7、设,函数的图象可能是( )
8、程序框图如下:
如果上述程序运行的结果S的值比2013小,若使输出的S最大,那么判断框中应填入( )
A. B. C. D.
9、图为一个空间几何体的三视图,其中俯视图是下边一个等边三角形,其内切圆的半径是1,正视图和侧视图是上边两个图形,数据如图,则此几何体的体积是( )
A. B. C. D.
10、在的展开式中,常数项为( )
A. B.5376 C. D.84
11、如果点P在平面区域上,点Q在曲线(x-1)2+(y-1)2=1上,那么|PQ|的最小值为( )
A.-1 B. C. D.-1
12、已知椭圆C:的左右焦点为,过的直线与圆相切于点A,并与椭圆C交与不同的两点P,Q,如图,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为 ( )
A. B. C. D.
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上
13、由曲线和直线所围成的面积为 。
14、如图,△ABC是圆内接三角形,圆心O在BC上,若AB=6,BD=3.6,将一颗豆子随机地扔到该圆内,用M表示事件“豆子落在△ABC内”,N表示事件“豆子落在△ABD内”,则P(N|M)= .
15、某市居民用户12月份燃气用量(单位:m3)的频率分布直方图如图所示,现抽取了500户进行调查,则用气量在[26,36)的户数为 。
16、在△ABC中,D为AB上任一点,h为AB边上的高,△ADC、△BDC、△ABC的内切圆半径分别为,则有如下的等式恒成立:.在三棱锥P-ABC中D位AB上任一点,h为过点P的三棱锥的高,三棱锥P-ADC、P-BDC、P-ABC的内切球的半径分别为,请类比平面三角形中的结论,写出类似的一个恒等式为 .
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤
17.(本题满分12分)已知函数,(其中),其部分图像如图所示.
(I)求函数的解析式;
(Ⅱ)已知横坐标分别为、、的三点、、都在函数的图像上,求的值.
18.(本题满分12分)
如图,在直角梯形ABCD中,AP/BC,,是AP的中点,E,F,G分别为PC,PD,CB的中点,将沿折起,使得平面ABCD.
(I)求证:AP//平面EFG;
(II)求二面角G-EF-D的大小.
19.(本题满分12分) 等差数列中,.
(Ⅰ)求数列的通项公式;
(Ⅱ)设,求数列的前n项和。
20.(本小题满分12分)
若盒中装有同一型号的灯泡共10只,其中有8只合格品,2只次品。
某工人师傅有放回地连续从该盒中取灯泡3次,每次取一只灯泡,求2次取到次品的概率;
(Ⅱ)某工人师傅有该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡所用灯泡只数的分布列和数学期望。
21.(本题满分13分)已知函数,.
(I)若函数,求函数的单调区间;
(Ⅱ)设直线为函数的图象上一点处的切线.证明:在区间上存在唯一的,使得直线l与曲线相切.
22.(本题满分13分)
已知椭圆过点,其长轴、焦距和短轴的长的平方依次成等差数列.直线与轴正半轴和轴分别交于点、,与椭圆分别交于点、,各点均不重合且满足
(I)求椭圆的标准方程;
(Ⅱ)若,试证明:直线过定点并求此定点.
参考答案
一选择题(每题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
A
B
C
B
B
C
B
A
C
C
二填空题(每题4分,满分16分,将答案填在答题纸上)
13. 14. 15. 16.
三解答题
17.【解析】(Ⅰ)由图可知, 最小正周期 所以.
又 ,且,
所以,.所以.
(Ⅱ)解法一:因为
所以,,
从而.
由得.
解法二:因为,
,所以,
,
,
则.
由得.
18.【解析】 (Ⅰ) 证明: 由题知,直线两两垂直,以为原点,以
为方向向量建立空间直角坐标系,如图所示.
则.
所以 . ……2分
设平面的法向量为,
取. ……………………4分
∵,
又平面,
//平面. ……………………6分
(Ⅱ)由已知底面ABCD是正方形,.又∵面ABCD,
.又,
平面PCD,向量是平面PCD的一个法向量, = . ……9分
又由(Ⅰ)知平面EFG的法向量为,
结合图知二面角的平面角为 ……………………12分
19.【解析】(Ⅰ)设数列
且,解得………2分
所以数列……4分
(Ⅱ)由(Ⅰ)可得,所以………6分
所以………
两式相减得……………10 分
…………12分
20.【解析】设一次取次品记为事件A,由古典概型概率公式得:……2 分
有放回连续取3次,其中2次取得次品记为事件B,由独立重复试验得:………4分
(2)依据知X的可能取值为1.2.3………5
且………6 ………7
………8
则X的分布列如下表:
X
1
2
3
p
……10分
………12分
21.【解析】(Ⅰ),.
∵且,∴,∴函数的单调递增区间为.
(Ⅱ)∵,∴,∴切线的方程为,
即, ①
设直线与曲线相切于点,∵,∴,∴.∴直线也为, 即, ②
由①②得,∴.
下证:在区间(1,+)上存在且唯一.
由(1)可知,在区间上递增.
又,,
结合零点存在性定理,说明方程必在区间上有唯一的根,这个根就是所求的唯一.故结论成立.
22.【解析】(Ⅰ)设椭圆方程为,焦距为2c, -------1分
由题意知 b=1,且,又
得. -------------3分
所以椭圆的方程为 ---------5分
(Ⅱ) 由题意设,设l方程为,
由知
∴,由题意,∴ -----------------7分
同理由知
∵,∴ (*) ------8分
联立得
∴需 (**)
且有 (***) -------10分
(***)代入(*)得,∴,
由题意,∴(满足(**)), ----------12分
得l方程为,过定点(1,0),即P为定点. ---------------13分
同课章节目录
