2022年初三中考专题一隐圆问题(1)—定点定长模型(含解析)
文档属性
| 名称 | 2022年初三中考专题一隐圆问题(1)—定点定长模型(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 547.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 12:05:30 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2022年初三中考专题一隐圆问题(1)—定点定长模型
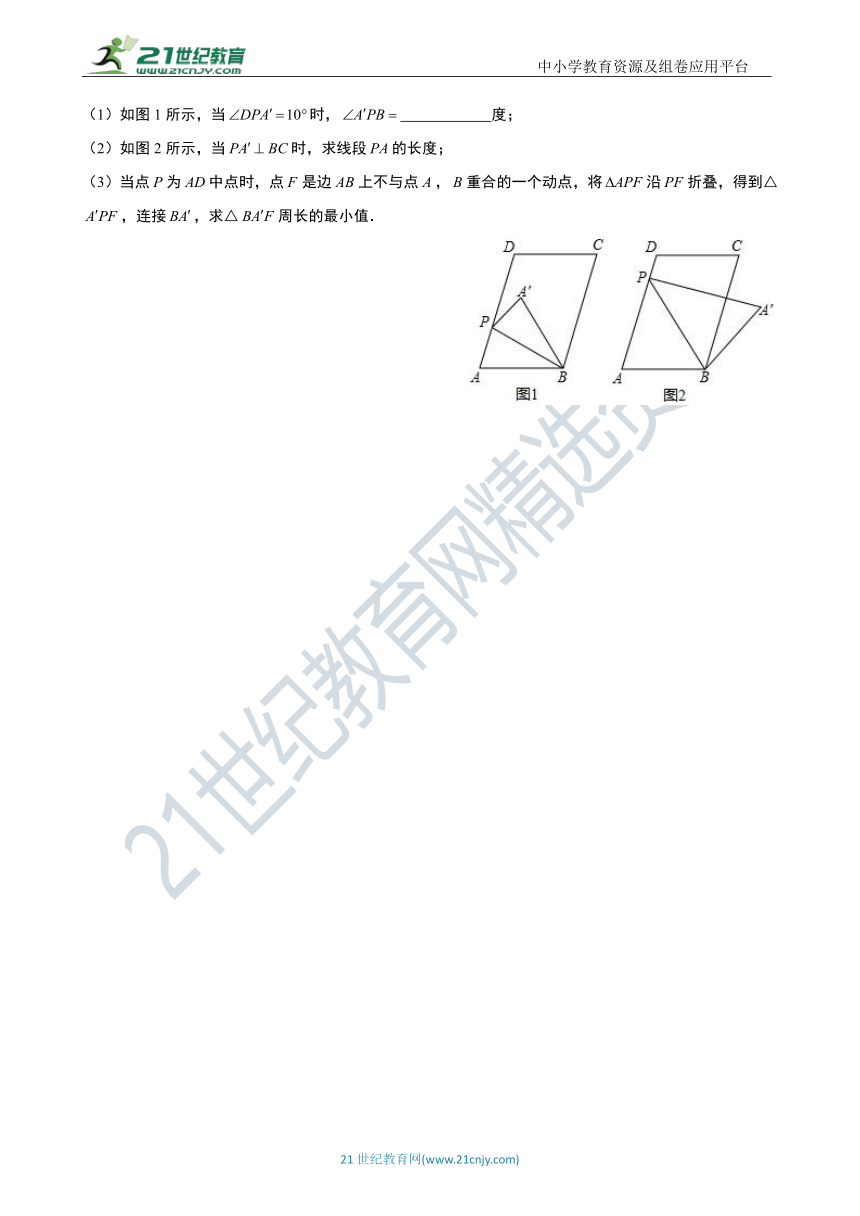
1.如图,在墙角的内部有一滑动杆,当端点沿直线向下滑动时,端点会随之自动地沿直线向右滑动,如果滑动杆从图中处滑动到处,那么滑动杆的中点所经过的路径是
A. B. C. D.
第1题图
2.如图,在矩形中,,,是边的中点,是线段上的动点,将沿所在直线折叠得到△,连接,则的最小值是
A.8 B.12 C. D.
第2题图 第3题图 第4题图
3.(2019 锦州)如图,在矩形中,,,是边的中点,是边上的动点,将沿所在直线折叠,得到△,连接,则的最小值是 .
4.如图,在菱形中,点是边的中点,动点在边上运动,以为折痕将折叠得到,连接,若,,则的最小值是 .
5.如图,在中,,,,是边上的动点(不与点重合),将沿所在的直线翻折,得到△,连接,则长度的最小值是 .
第5题图 第6题图
6.如图,在矩形中,,,是的中点,是边上的动点,将沿所在直线折叠,得到△,连接,则的最小值是 .
7.如图,在平行四边形中,,,,是射线上一点,连接,沿将折叠,得△.
(1)如图1所示,当时, 度;
(2)如图2所示,当时,求线段的长度;
(3)当点为中点时,点是边上不与点,重合的一个动点,将沿折叠,得到△,连接,求△周长的最小值.
【参考答案】
1、【解答】解:连接、,如图,
,为中点,
,
当端点沿直线向下滑动时,的中点到的距离始终为定长,
滑动杆的中点所经过的路径是以为圆心,为半径的一段圆弧.
故选:.
2、【解答】解:如图,的运动轨迹是以为圆心为半径的圆弧,
当点落在上时,取得最小值.
根据折叠的性质,可得△,
,,
是边的中点,,
,
,
,
.
故选:.
3、【解答】解:如图,
以为折痕将折叠得到,
,
点在以为圆心,为半径的半圆上,
,
当,,在同一直线上时,最短,
如图,过点作于点,
在边长为4的菱形中,,为的中点,
,,
,,
,
,
的最小值为,
故答案为:.
4、【解答】解:四边形是矩形
,,
是边的中点,
将沿所在直线折叠,
点在以点为圆心,为半径的圆上,
如图,当点在线段上时,有最小值,
的最小值
故答案为:
5、【解答】解:在中,由勾股定理可知:,
由轴对称的性质可知:,
当、、三点在一条直线上时,有最小值,
.
故答案为:1.
6、【解答】解:四边形是矩形,
,,
是边的中点,
,
将沿所在直线折叠,
,
点在以点为圆心,为半径的圆上,
如图,当点在线段上时,有最小值,
,
的最小值,故答案为:.
7、【解答】解:(1)如图1中,
,
,
由翻折的性质可知:.
故答案为85.
(2)如图2中,作于.
在中,,,,
,,
四边形是平行四边形,
,
,
,
,
,
,
.
(3)如图3中,作于,连接.
,,
,
,
,
由翻折可知:,,
的周长,
当的长度最小时,的周长最小,
,
,
的最小值为,
的周长的最小值为.
21世纪教育网(www.21cnjy.com)
2022年初三中考专题一隐圆问题(1)—定点定长模型
1.如图,在墙角的内部有一滑动杆,当端点沿直线向下滑动时,端点会随之自动地沿直线向右滑动,如果滑动杆从图中处滑动到处,那么滑动杆的中点所经过的路径是
A. B. C. D.
第1题图
2.如图,在矩形中,,,是边的中点,是线段上的动点,将沿所在直线折叠得到△,连接,则的最小值是
A.8 B.12 C. D.
第2题图 第3题图 第4题图
3.(2019 锦州)如图,在矩形中,,,是边的中点,是边上的动点,将沿所在直线折叠,得到△,连接,则的最小值是 .
4.如图,在菱形中,点是边的中点,动点在边上运动,以为折痕将折叠得到,连接,若,,则的最小值是 .
5.如图,在中,,,,是边上的动点(不与点重合),将沿所在的直线翻折,得到△,连接,则长度的最小值是 .
第5题图 第6题图
6.如图,在矩形中,,,是的中点,是边上的动点,将沿所在直线折叠,得到△,连接,则的最小值是 .
7.如图,在平行四边形中,,,,是射线上一点,连接,沿将折叠,得△.
(1)如图1所示,当时, 度;
(2)如图2所示,当时,求线段的长度;
(3)当点为中点时,点是边上不与点,重合的一个动点,将沿折叠,得到△,连接,求△周长的最小值.
【参考答案】
1、【解答】解:连接、,如图,
,为中点,
,
当端点沿直线向下滑动时,的中点到的距离始终为定长,
滑动杆的中点所经过的路径是以为圆心,为半径的一段圆弧.
故选:.
2、【解答】解:如图,的运动轨迹是以为圆心为半径的圆弧,
当点落在上时,取得最小值.
根据折叠的性质,可得△,
,,
是边的中点,,
,
,
,
.
故选:.
3、【解答】解:如图,
以为折痕将折叠得到,
,
点在以为圆心,为半径的半圆上,
,
当,,在同一直线上时,最短,
如图,过点作于点,
在边长为4的菱形中,,为的中点,
,,
,,
,
,
的最小值为,
故答案为:.
4、【解答】解:四边形是矩形
,,
是边的中点,
将沿所在直线折叠,
点在以点为圆心,为半径的圆上,
如图,当点在线段上时,有最小值,
的最小值
故答案为:
5、【解答】解:在中,由勾股定理可知:,
由轴对称的性质可知:,
当、、三点在一条直线上时,有最小值,
.
故答案为:1.
6、【解答】解:四边形是矩形,
,,
是边的中点,
,
将沿所在直线折叠,
,
点在以点为圆心,为半径的圆上,
如图,当点在线段上时,有最小值,
,
的最小值,故答案为:.
7、【解答】解:(1)如图1中,
,
,
由翻折的性质可知:.
故答案为85.
(2)如图2中,作于.
在中,,,,
,,
四边形是平行四边形,
,
,
,
,
,
,
.
(3)如图3中,作于,连接.
,,
,
,
,
由翻折可知:,,
的周长,
当的长度最小时,的周长最小,
,
,
的最小值为,
的周长的最小值为.
21世纪教育网(www.21cnjy.com)
同课章节目录
