上海市浦东新区上海市建平实验中学2021-2022学年九年级下学期中考模拟数学试卷(Word版 含答案)
文档属性
| 名称 | 上海市浦东新区上海市建平实验中学2021-2022学年九年级下学期中考模拟数学试卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 771.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-23 10:39:51 | ||
图片预览



文档简介
上海建平实验2021-2022学年九年级第二学期中考模拟试卷
一、选择题(本大题共有6题,每题4分,满分24分)
1.下列运算正确的是( )
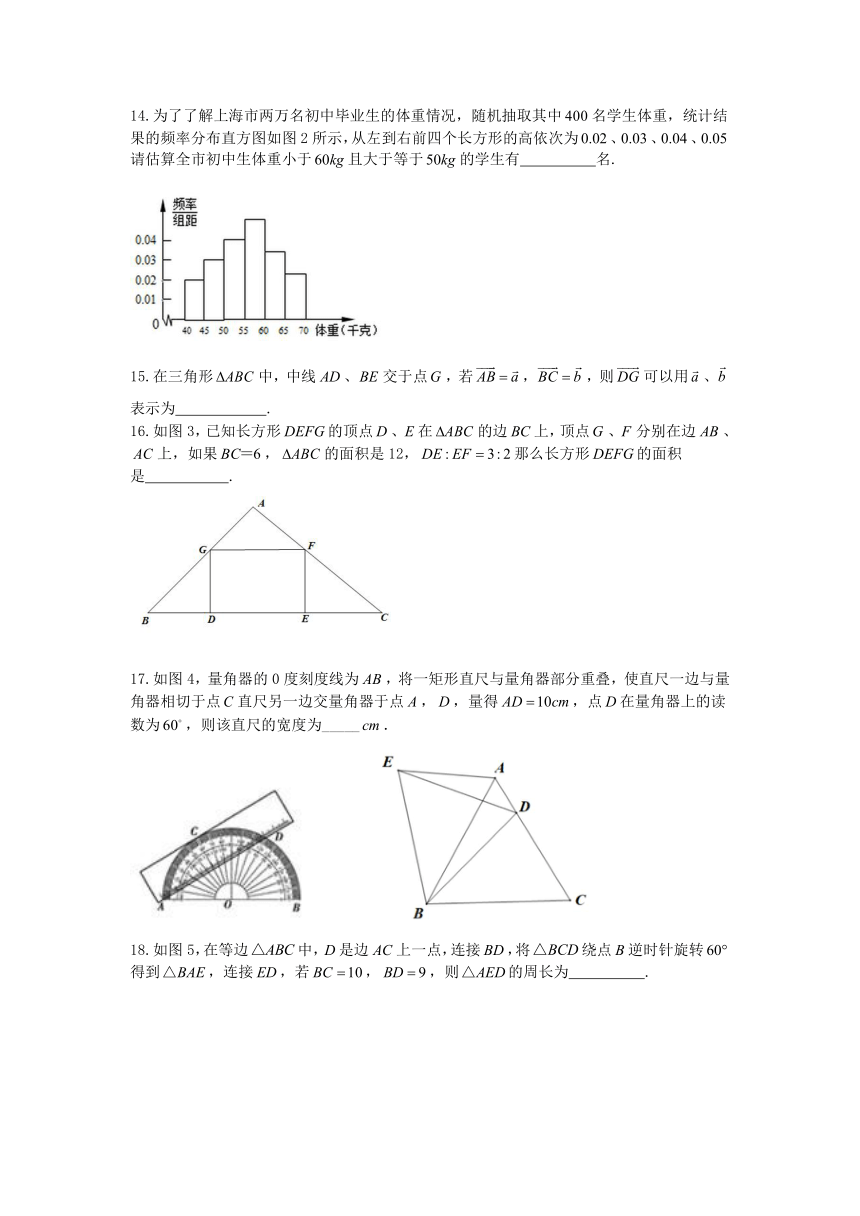
(A) (B) (C) (D)
2.下列关于的一元二次方程有实数根的是( )
(A) (B) (C) (D)
3.如果将抛物线向上平移个单位,那么所得抛物线的表达式( )
(A) (B) (C) (D)
4.数据0、、、、、、的平均数和中位数是( )
(A); (B); (C); (D);
5.已知点,,如果⊙的半径为,⊙的半径为,则⊙与⊙的位置关系是( )
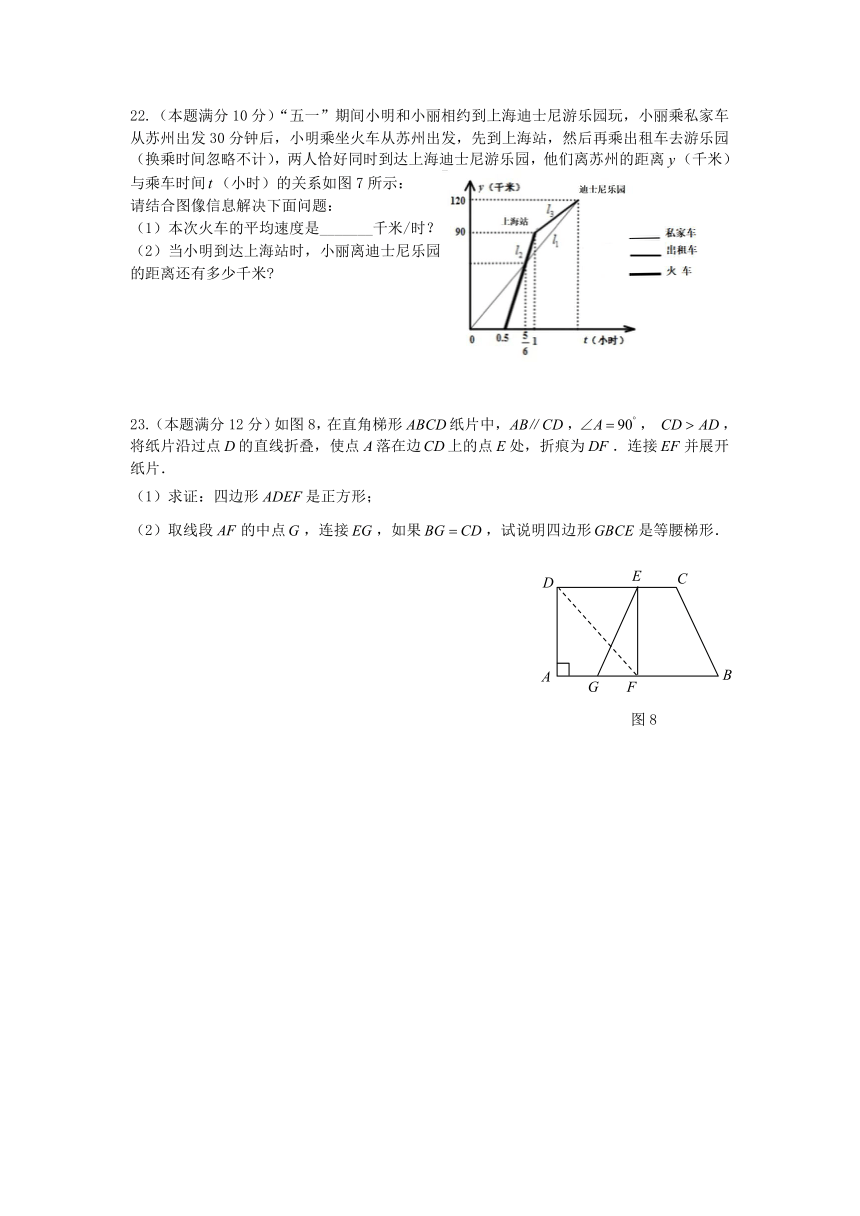
(A)内切 (B)相交 (C)外切 (D)外离
6.下列命题中,假命题是( )
(A)菱形对角线互相垂直平分
(B)平行四边形对角线互相平分
(C)经过半径的端点且垂直于这条半径的直线是圆的切线
(D)在等圆中,相等的弦所对的圆心角相等
二、填空题(本大题共有12题,每题4分,满分48分)
7.已知,那么 .
8.因式分解: .
9.不等式组的解集是 .
10.如果反比例函数的图像经过点,,则_______.(填“”或“”)
11.从、、、、、中,任取一个数,是素数的概率是 .
12.如图1,直线,直线交, ,于点,,;直线交, ,于点,,.已知,则=__________.
13.某公司卖出一批货物,第一季度卖出100万件,第二、三季度卖出的件数连续增长,第三季度卖出144万件.设第二、三季度平均增长率为,则根据题意可列方程为_____________.
14.为了了解上海市两万名初中毕业生的体重情况,随机抽取其中名学生体重,统计结果的频率分布直方图如图2所示,从左到右前四个长方形的高依次为、、、请估算全市初中生体重小于且大于等于的学生有 名.
15.在三角形中,中线、交于点,若,,则可以用、表示为 .
16.如图3,已知长方形的顶点、在的边上,顶点、分别在边、上,如果,的面积是12,那么长方形的面积是 .
17.如图4,量角器的0度刻度线为,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点直尺另一边交量角器于点,,量得,点在量角器上的读数为,则该直尺的宽度为_____.
18.如图5,在等边中,是边上一点,连接,将绕点逆时针旋转得到,连接,若,,则的周长为 .
三、填空题(本大题共7小题,满分78分)
19.(本题满分10分)计算:
20.(本题满分10分)解方程组:
21.(本题满分10分)如图6,在中,,,点为中点,联结,过点作,交的延长线于点.
(1)若,求的面积;
(2)求的值.
22.(本题满分10分)“五一”期间小明和小丽相约到上海迪士尼游乐园玩,小丽乘私家车从苏州出发30分钟后,小明乘坐火车从苏州出发,先到上海站,然后再乘出租车去游乐园(换乘时间忽略不计),两人恰好同时到达上海迪士尼游乐园,他们离苏州的距离(千米)与乘车时间(小时)的关系如图7所示:
请结合图像信息解决下面问题:
(1)本次火车的平均速度是_______千米/时?
(2)当小明到达上海站时,小丽离迪士尼乐园
的距离还有多少千米
23.(本题满分12分)如图8,在直角梯形纸片中,,, ,将纸片沿过点的直线折叠,使点落在边上的点处,折痕为.连接并展开纸片.
(1)求证:四边形是正方形;
(2)取线段的中点,连接,如果,试说明四边形是等腰梯形.
图8
24.(本题满分12分)在平面直角坐标系中,抛物线经过点,与轴交于点、(在的左侧),与轴交于点,且,抛物线顶点为点.
(1)求抛物线的解析式和顶点坐标;
(2)求的面积;
(3)在对称轴上找到一点,使得,求点的坐标.
25.(本题满分14分)已知为等腰直角三角形,,,延长至点,以为直径作圆,圆心为,联结与圆交于点,联结并延长交圆与点.
(1)联结,求证: ;
(2)设,,求与的函数关系式;
(3)当时,求的长.
-参考答案
一、选择题
1-6CAABAC
二、填空题
7.;8.;9.;10.;11.;12.2;13.;
14.;15.;16.6;17.;18.19
三、解答题
19.【答案】
【解析】原式=
=
=
20.【答案】,.
【解析】由题意得:
所以可得:或
解方程组得:,.
21.【答案】(1);(2)
【解析】(1)在中,
∴
又∵点为中点
∴
在中, ,即
解得:
∴
∴
(2)∵ ,
∴
∴
∴,即
由(1)可得:
∴
故的值为.
22.【答案】(1)千米/小时(2)48千米
【解析】(1)千米/小时
(2)设的解析式为,当时,y=0;当t=1时,y=90,
得:解得:,.
故把代入,得y=60,
设的解析式,当时,y=60,得:
∴a=72,∴y=72t,
当t=1,y=72,∴120-72=48(千米)
答:当小明到达上海站时,小丽离迪士尼乐园的距离还有48千米.
23.【答案】见解析
【解析】(1)
∴
∵
∴
∴四边形为矩形
又∵
∴为正方形
(2)过作,垂足为
∵,
∴是梯形
∵
∴
又∵
∴ ..为矩形
∴
又∵
∴
∴
又∵
∴
又∵,
∴
∴
∴四边形为等腰梯形
24.【答案】(1);(2);(3)或.
【解析】(1)
将、代入解析式中,
解得
顶点
(2)
作轴,垂足为点
(3)由(2)已知,为直角三角形,
令对称轴与轴交点为,则
或
25.【答案】(1)略(2)(3)
【解析】(1)联结,∴
∴,
∴
∴
∴
∴
(2)∵∴
∴ ∴
∴
∴
在中,,
又∵
∴
(3)记与的交点为,与的交点为
∵
∴,,
∴
所以
联结,∴
∴,
∴
∴
∴
∴,
∴
∴
∴,∴,∴
过点作,
∴
一、选择题(本大题共有6题,每题4分,满分24分)
1.下列运算正确的是( )
(A) (B) (C) (D)
2.下列关于的一元二次方程有实数根的是( )
(A) (B) (C) (D)
3.如果将抛物线向上平移个单位,那么所得抛物线的表达式( )
(A) (B) (C) (D)
4.数据0、、、、、、的平均数和中位数是( )
(A); (B); (C); (D);
5.已知点,,如果⊙的半径为,⊙的半径为,则⊙与⊙的位置关系是( )
(A)内切 (B)相交 (C)外切 (D)外离
6.下列命题中,假命题是( )
(A)菱形对角线互相垂直平分
(B)平行四边形对角线互相平分
(C)经过半径的端点且垂直于这条半径的直线是圆的切线
(D)在等圆中,相等的弦所对的圆心角相等
二、填空题(本大题共有12题,每题4分,满分48分)
7.已知,那么 .
8.因式分解: .
9.不等式组的解集是 .
10.如果反比例函数的图像经过点,,则_______.(填“”或“”)
11.从、、、、、中,任取一个数,是素数的概率是 .
12.如图1,直线,直线交, ,于点,,;直线交, ,于点,,.已知,则=__________.
13.某公司卖出一批货物,第一季度卖出100万件,第二、三季度卖出的件数连续增长,第三季度卖出144万件.设第二、三季度平均增长率为,则根据题意可列方程为_____________.
14.为了了解上海市两万名初中毕业生的体重情况,随机抽取其中名学生体重,统计结果的频率分布直方图如图2所示,从左到右前四个长方形的高依次为、、、请估算全市初中生体重小于且大于等于的学生有 名.
15.在三角形中,中线、交于点,若,,则可以用、表示为 .
16.如图3,已知长方形的顶点、在的边上,顶点、分别在边、上,如果,的面积是12,那么长方形的面积是 .
17.如图4,量角器的0度刻度线为,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点直尺另一边交量角器于点,,量得,点在量角器上的读数为,则该直尺的宽度为_____.
18.如图5,在等边中,是边上一点,连接,将绕点逆时针旋转得到,连接,若,,则的周长为 .
三、填空题(本大题共7小题,满分78分)
19.(本题满分10分)计算:
20.(本题满分10分)解方程组:
21.(本题满分10分)如图6,在中,,,点为中点,联结,过点作,交的延长线于点.
(1)若,求的面积;
(2)求的值.
22.(本题满分10分)“五一”期间小明和小丽相约到上海迪士尼游乐园玩,小丽乘私家车从苏州出发30分钟后,小明乘坐火车从苏州出发,先到上海站,然后再乘出租车去游乐园(换乘时间忽略不计),两人恰好同时到达上海迪士尼游乐园,他们离苏州的距离(千米)与乘车时间(小时)的关系如图7所示:
请结合图像信息解决下面问题:
(1)本次火车的平均速度是_______千米/时?
(2)当小明到达上海站时,小丽离迪士尼乐园
的距离还有多少千米
23.(本题满分12分)如图8,在直角梯形纸片中,,, ,将纸片沿过点的直线折叠,使点落在边上的点处,折痕为.连接并展开纸片.
(1)求证:四边形是正方形;
(2)取线段的中点,连接,如果,试说明四边形是等腰梯形.
图8
24.(本题满分12分)在平面直角坐标系中,抛物线经过点,与轴交于点、(在的左侧),与轴交于点,且,抛物线顶点为点.
(1)求抛物线的解析式和顶点坐标;
(2)求的面积;
(3)在对称轴上找到一点,使得,求点的坐标.
25.(本题满分14分)已知为等腰直角三角形,,,延长至点,以为直径作圆,圆心为,联结与圆交于点,联结并延长交圆与点.
(1)联结,求证: ;
(2)设,,求与的函数关系式;
(3)当时,求的长.
-参考答案
一、选择题
1-6CAABAC
二、填空题
7.;8.;9.;10.;11.;12.2;13.;
14.;15.;16.6;17.;18.19
三、解答题
19.【答案】
【解析】原式=
=
=
20.【答案】,.
【解析】由题意得:
所以可得:或
解方程组得:,.
21.【答案】(1);(2)
【解析】(1)在中,
∴
又∵点为中点
∴
在中, ,即
解得:
∴
∴
(2)∵ ,
∴
∴
∴,即
由(1)可得:
∴
故的值为.
22.【答案】(1)千米/小时(2)48千米
【解析】(1)千米/小时
(2)设的解析式为,当时,y=0;当t=1时,y=90,
得:解得:,.
故把代入,得y=60,
设的解析式,当时,y=60,得:
∴a=72,∴y=72t,
当t=1,y=72,∴120-72=48(千米)
答:当小明到达上海站时,小丽离迪士尼乐园的距离还有48千米.
23.【答案】见解析
【解析】(1)
∴
∵
∴
∴四边形为矩形
又∵
∴为正方形
(2)过作,垂足为
∵,
∴是梯形
∵
∴
又∵
∴ ..为矩形
∴
又∵
∴
∴
又∵
∴
又∵,
∴
∴
∴四边形为等腰梯形
24.【答案】(1);(2);(3)或.
【解析】(1)
将、代入解析式中,
解得
顶点
(2)
作轴,垂足为点
(3)由(2)已知,为直角三角形,
令对称轴与轴交点为,则
或
25.【答案】(1)略(2)(3)
【解析】(1)联结,∴
∴,
∴
∴
∴
∴
(2)∵∴
∴ ∴
∴
∴
在中,,
又∵
∴
(3)记与的交点为,与的交点为
∵
∴,,
∴
所以
联结,∴
∴,
∴
∴
∴
∴,
∴
∴
∴,∴,∴
过点作,
∴
同课章节目录
