2021—2022学年人教版数学八年级下册19.3课题学习 选择方案 课件(16张ppt)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册19.3课题学习 选择方案 课件(16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 12:17:27 | ||
图片预览




文档简介
(共16张PPT)
第十九章
课题学习 选择方案
学习目标
1】会用一次函数知识解决方案选择问题,体会函数模型思想。
2】能从不同角度思考问题,优化解决问题的方法。
3】通进行解决问题的反思,总结解决问题的方法。
做一件事情,有时有不同的实施方案,比较这些方案,从中选择最佳方案作为行动计划,是非常必要的。应用数学的知识和方法对各种方案进行比较分析,可以帮助我们清楚地认识各种方案,作出理性的决策。为此,提出一个现实问题以供探究,请看下面问题。
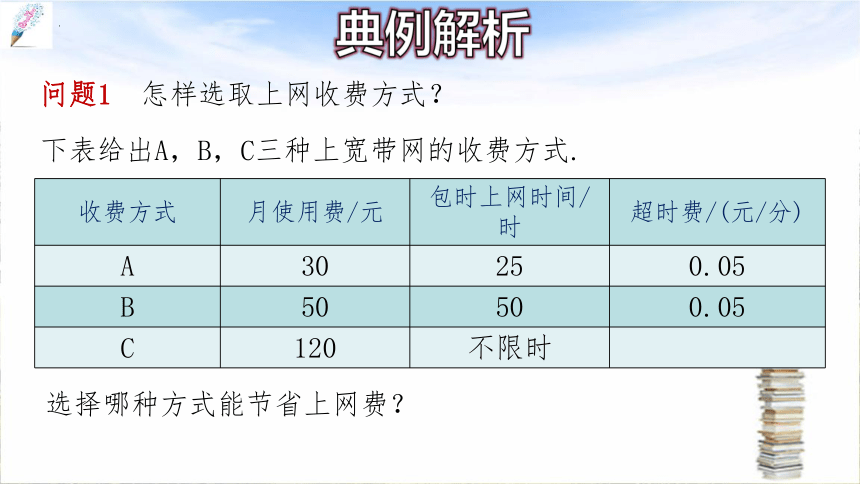
问题1 怎样选取上网收费方式?
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
下表给出A,B,C三种上宽带网的收费方式.
典例解析
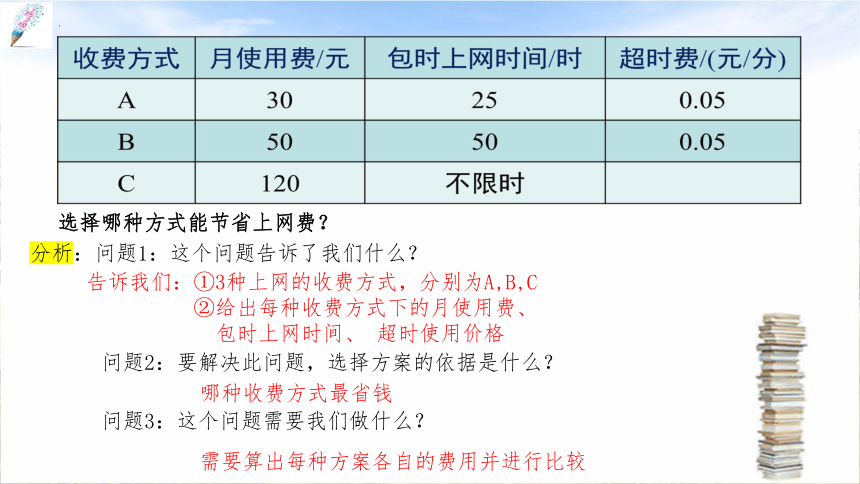
选择哪种方式能节省上网费?
函数是反映变量之间对应关系和变化规律的重要模型。
利用函数模型解决实际问题的一般步骤:
①设:设变量(自变量和因变量)
②建:建立因变量与自变量的函数关系,把实际问题转化为函数问题。
③解:利用函数的性质,解决函数问题。
④释:解释函数问题的实际意义,得到实际问题的解。
分析:问题1:这个问题告诉了我们什么?
告诉我们:①3种上网的收费方式,分别为A,B,C
②给出每种收费方式下的月使用费、
包时上网时间、 超时使用价格
问题3:这个问题需要我们做什么?
哪种收费方式最省钱
选择哪种方式能节省上网费?
问题2:要解决此问题,选择方案的依据是什么?
需要算出每种方案各自的费用并进行比较
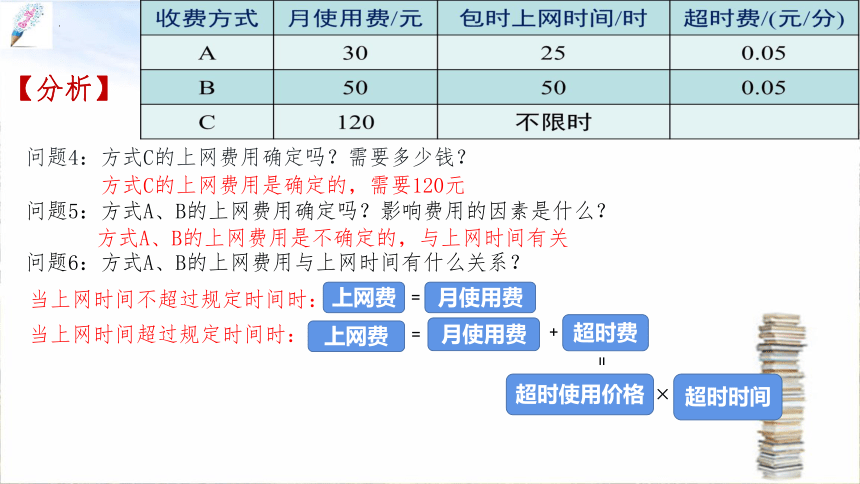
问题4:方式C的上网费用确定吗?需要多少钱?
方式C的上网费用是确定的,需要120元
问题5:方式A、B的上网费用确定吗?影响费用的因素是什么?
问题6:方式A、B的上网费用与上网时间有什么关系?
【分析】
当上网时间不超过规定时间时:
方式A、B的上网费用是不确定的,与上网时间有关
当上网时间超过规定时间时:
上网费
=
月使用费
上网费
=
月使用费
+
超时费
超时使用价格
=
×
超时时间
典例解析
(2)设上网时间为th,你能列表表示方式A、B的上网费用与上网时间的关系式吗
月使用费/元 上网时间/h 超时费用/元 总费用/元
方式A
方式B
方式C
30
0≤t≤25
0
30
t>25
3(t-25)
30+3(t-25)
120
50
0≤t≤50
0
50
t>50
3(t-50)
50+3(t-50)
不限时
0
120
(2)设上网时间为th,方式A的上网费用为 元,方式B的上网费用为 元,方式C的上网费用为 元。 你能用函数解析式表示上网费用与上网时间之间的数量关系吗?
o
t/h
y/元
10
10
25
50
50
120
70
100
y1
70
y2
y3
分别找出函数的交点M,N,P,对函数图象进行分割:
M
N
P
求出交点M,P的坐标
y3=120 (t≥0)
①解方程组
②解方程组
要确定选择方案,就是在t﹥0时比较 , , 的大小,
解决此函数问题,需画出函数图象,观察函数图象的
基础上对上网时间分段讨论。
o
t/h
y/元
10
10
25
50
50
120
70
100
y1
70
y2
y3
M
N
P
①当__________时,选择方式A最省钱.
③当__________时,选择方式B最省钱.
②当__________时,选择方式A,B一样省钱.
④当__________时,选择方式B.C一样省钱.
⑤当__________时,选择方式C最省钱.
o
t/h
y/元
10
10
25
50
50
120
70
100
y1
70
y2
y3
M
N
P
①当__________时,选择方式A最省钱.
③当__________时,选择方式B最省钱.
②当__________时,选择方式A,B一样省钱.
④当__________时,选择方式B.C一样省钱.
⑤当__________时,选择方式C最省钱.
解:设上网时间为th,方式A的上网费用为 元,方式B的上网费用为 元,方式C的上网费用为 元。
画出函数的图象,图象的交点记为M,N,P
①解方程组
②解方程组
这个实际问题的解决过程中是怎样思考的?
小结
实际问题
函数问题
设变量
找对应关系
函数问题的解
实际问题的解
解释
实际意义
某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费15元,另收通话费为0.2元/分;
B方案: 零月租费,通话费为0.3元/分.
(1)试写出A,B两种方案所付话费y(元)与通话 时间t(分)之间的函数关系式;
(2)在同一坐标系画出这两个函数的图象,并指出哪种付费方式合算?
A方案: y1 = 15+0.2t(t≥0)
B方案:y2 = 0.3t(t≥0).
跟踪练习
解:(1) A方案: y1 = 15+0.2t(t≥0),
B方案:
y2 = 0.3t(t≥0).
(2)画函数的图象如下:
t(分)
O
50
150
100
10
20
y(元)
50
30
40
●
●
y1 = 15+0.2t
y2 = 0.3t
●
观察图象,可知:
当通话时间为150分时,选择A或B方案费用一样;
当通话时间少于150分时,选择B方案费合算;
当通话时间多于150分时,选择A方案合算.
谢谢观看!
第十九章
课题学习 选择方案
学习目标
1】会用一次函数知识解决方案选择问题,体会函数模型思想。
2】能从不同角度思考问题,优化解决问题的方法。
3】通进行解决问题的反思,总结解决问题的方法。
做一件事情,有时有不同的实施方案,比较这些方案,从中选择最佳方案作为行动计划,是非常必要的。应用数学的知识和方法对各种方案进行比较分析,可以帮助我们清楚地认识各种方案,作出理性的决策。为此,提出一个现实问题以供探究,请看下面问题。
问题1 怎样选取上网收费方式?
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
下表给出A,B,C三种上宽带网的收费方式.
典例解析
选择哪种方式能节省上网费?
函数是反映变量之间对应关系和变化规律的重要模型。
利用函数模型解决实际问题的一般步骤:
①设:设变量(自变量和因变量)
②建:建立因变量与自变量的函数关系,把实际问题转化为函数问题。
③解:利用函数的性质,解决函数问题。
④释:解释函数问题的实际意义,得到实际问题的解。
分析:问题1:这个问题告诉了我们什么?
告诉我们:①3种上网的收费方式,分别为A,B,C
②给出每种收费方式下的月使用费、
包时上网时间、 超时使用价格
问题3:这个问题需要我们做什么?
哪种收费方式最省钱
选择哪种方式能节省上网费?
问题2:要解决此问题,选择方案的依据是什么?
需要算出每种方案各自的费用并进行比较
问题4:方式C的上网费用确定吗?需要多少钱?
方式C的上网费用是确定的,需要120元
问题5:方式A、B的上网费用确定吗?影响费用的因素是什么?
问题6:方式A、B的上网费用与上网时间有什么关系?
【分析】
当上网时间不超过规定时间时:
方式A、B的上网费用是不确定的,与上网时间有关
当上网时间超过规定时间时:
上网费
=
月使用费
上网费
=
月使用费
+
超时费
超时使用价格
=
×
超时时间
典例解析
(2)设上网时间为th,你能列表表示方式A、B的上网费用与上网时间的关系式吗
月使用费/元 上网时间/h 超时费用/元 总费用/元
方式A
方式B
方式C
30
0≤t≤25
0
30
t>25
3(t-25)
30+3(t-25)
120
50
0≤t≤50
0
50
t>50
3(t-50)
50+3(t-50)
不限时
0
120
(2)设上网时间为th,方式A的上网费用为 元,方式B的上网费用为 元,方式C的上网费用为 元。 你能用函数解析式表示上网费用与上网时间之间的数量关系吗?
o
t/h
y/元
10
10
25
50
50
120
70
100
y1
70
y2
y3
分别找出函数的交点M,N,P,对函数图象进行分割:
M
N
P
求出交点M,P的坐标
y3=120 (t≥0)
①解方程组
②解方程组
要确定选择方案,就是在t﹥0时比较 , , 的大小,
解决此函数问题,需画出函数图象,观察函数图象的
基础上对上网时间分段讨论。
o
t/h
y/元
10
10
25
50
50
120
70
100
y1
70
y2
y3
M
N
P
①当__________时,选择方式A最省钱.
③当__________时,选择方式B最省钱.
②当__________时,选择方式A,B一样省钱.
④当__________时,选择方式B.C一样省钱.
⑤当__________时,选择方式C最省钱.
o
t/h
y/元
10
10
25
50
50
120
70
100
y1
70
y2
y3
M
N
P
①当__________时,选择方式A最省钱.
③当__________时,选择方式B最省钱.
②当__________时,选择方式A,B一样省钱.
④当__________时,选择方式B.C一样省钱.
⑤当__________时,选择方式C最省钱.
解:设上网时间为th,方式A的上网费用为 元,方式B的上网费用为 元,方式C的上网费用为 元。
画出函数的图象,图象的交点记为M,N,P
①解方程组
②解方程组
这个实际问题的解决过程中是怎样思考的?
小结
实际问题
函数问题
设变量
找对应关系
函数问题的解
实际问题的解
解释
实际意义
某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费15元,另收通话费为0.2元/分;
B方案: 零月租费,通话费为0.3元/分.
(1)试写出A,B两种方案所付话费y(元)与通话 时间t(分)之间的函数关系式;
(2)在同一坐标系画出这两个函数的图象,并指出哪种付费方式合算?
A方案: y1 = 15+0.2t(t≥0)
B方案:y2 = 0.3t(t≥0).
跟踪练习
解:(1) A方案: y1 = 15+0.2t(t≥0),
B方案:
y2 = 0.3t(t≥0).
(2)画函数的图象如下:
t(分)
O
50
150
100
10
20
y(元)
50
30
40
●
●
y1 = 15+0.2t
y2 = 0.3t
●
观察图象,可知:
当通话时间为150分时,选择A或B方案费用一样;
当通话时间少于150分时,选择B方案费合算;
当通话时间多于150分时,选择A方案合算.
谢谢观看!
