甘肃省张掖市临泽县2021-2022学年高二下学期期中考试数学(文)试题(Word版含答案)
文档属性
| 名称 | 甘肃省张掖市临泽县2021-2022学年高二下学期期中考试数学(文)试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 481.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 00:00:00 | ||
图片预览



文档简介
临泽县2021-2022学年高二下学期期中考试
数学试卷(文科)
一、选择题
1.已知集合,则( )
A. B. C. D.
2.已知复数(其中i为虚数单位),则z的共轭复数为( )
A. B. C. D.
3.我国古代数学名著《数书九章》是南宋数学家秦九韶所著数学著作,书中共列算题81问,分为9类.全书采用问题集的形式,并不按数学方法来分类.题文也不只谈数学,还涉及自然现象和社会生活,成为了解当时社会政治和经济生活的重要参考文献.《数书九章》中有“米谷粒分”一题,现有类似的题:粮仓开仓收粮,粮农送来米1634石,验得米夹谷,抽样取米一把,数得254粒夹谷25粒,则这批米内夹谷约为( )
A.158石 B.159石 C.160石 D.161石
4.设、是两定点,,动点P满足,则动点P的轨迹是( )
A.双曲线 B.直线 C.线段 D.射线
5.在等比数列中,已知,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
6.已知,则a,b,c的大小关系为( )
A. B. C. D.
7.已知,则( )
A. B. C. D.
8.直线平分圆的周长,过点作圆C的一条切线,切点为Q,则( )
A.5 B.4 C.3 D.2
9.设x,y满足约束条件,则的范围是( )
A. B. C. D.
10.如图,在直三棱柱中,D为的中点,,则异面直线与所成的角为( )
A. B. C. D.
11.已知是双曲线的上、下焦点,点M是该双曲线的一条渐近线上的一点,并且以线段为直径的圆经过点M,则下列说法不正确的是( )
A.双曲线C的渐近线方程为 B.点M的横坐标为
C.的面积为 D.以为直径的圆的方程为
12.若函数在区间上有2个零点,则的取值范围是( )
A. B. C. D.
二、填空题
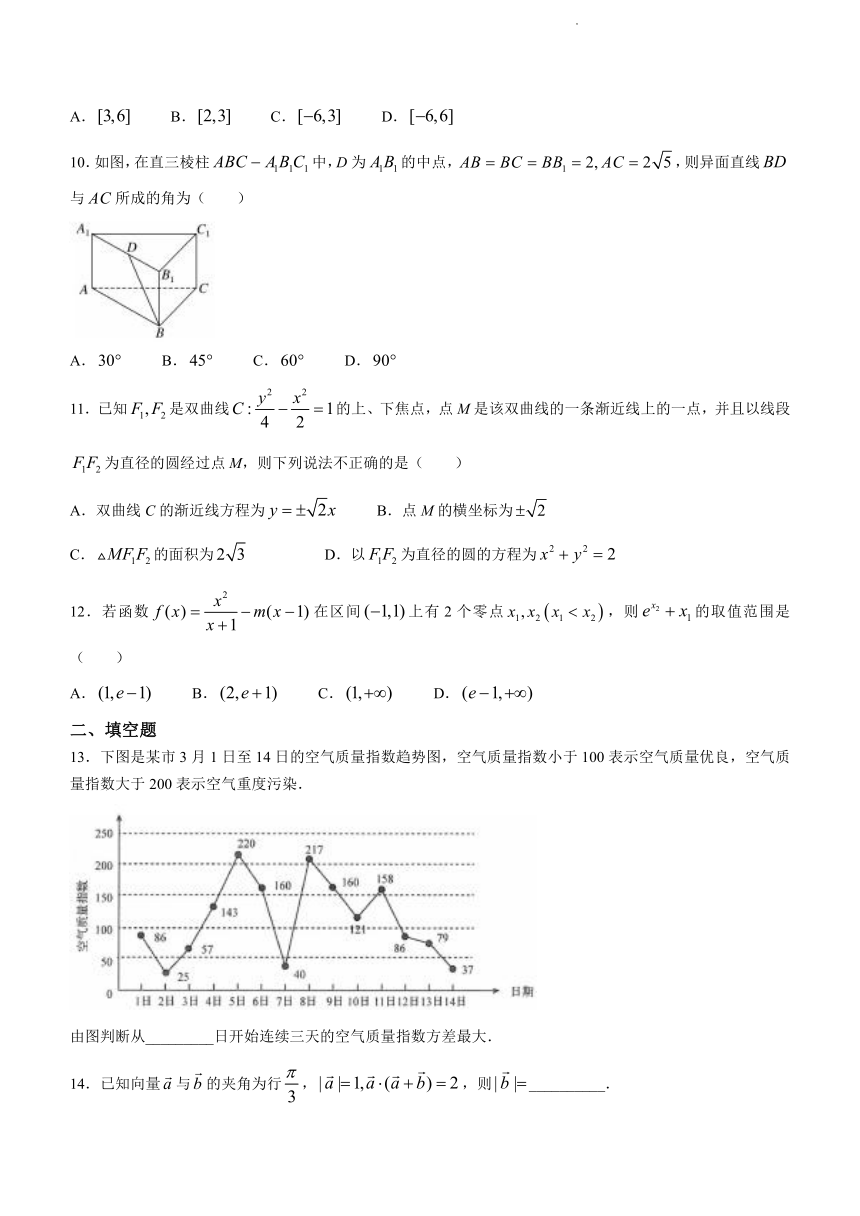
13.下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.
由图判断从_________日开始连续三天的空气质量指数方差最大.
14.已知向量与的夹角为行,,则__________.
15.词语“堑堵”、“阳马”、“鳖臑”等出现自中国数学名著《九章算术·商功》,是古代人对一些特殊锥体的称呼.在《九章算术·商功》中,把四个面都是直角三角形的四面体称为“鳖臑”.现有如图所示的“鳖臑”四面体,其中平面,则四面体的外接球的表面积为__________.
16.已知为等差数列的前n项和,,设,且数列的前n项和为,则使恒成立的实数的取值范围是__________.
三、解答题
17.在中,角A,B,C所对的边分别为a,b,c,已知.
(1)求A;
(2)若,求的面积.
18.为调查电影《长津湖》在国庆假期的上映满意度,抽取了男女各25人对这部电影的满意度进行调查,统计数据如表所示.
满意 非常满意 合度
男 18 7 25
女 6 19 25
合计 24 26 50
(1)如果随机抽查1人,那么抽到满意的概率是多少?抽到非常满意的女性的概率是多少?
(2)能否有99.9%的把握认为性别和满意度有关?
0.050 0.010 0.001
k 3.841 6.635 10.828
附:.
19.如图,在三棱锥中,平面.
(1)求证:平面平面;
(2)若,M是的中点,求与平面所成角的正切值.
20.已知抛物线的焦点为F,P是抛物线C上一点,且满足.
(1)求抛物线C的方程;
(2)已知斜率为2的直线l与抛物线C交于A,B两点,若成等差数列,求该数列的公差.
21.已知函数,且函数在处的切线为.
(1)求a,b的值并分析函数的单调性;
(2)若函数恰有两个零点,求实数m的取值范围.
(请考生在两题中任选一题作答,如果多作按所作第一题计分)
22-1选做题【选修4-4坐标系与参数方程】在直角坐标系中,圆C的参数方程为:(为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
①求圆C的极坐标方程;
②直线的极坐标方程是,射线:与圆C的交点为O,P,与直线l的交点为Q,求线的长.
22-2【选修4-5.不等式选讲】设函数.
①求的解集;
②若不等式对任意实数x恒成立,求实数m的取值范围.
临泽县2021-2022学年高二下学期期中考试
数学答案(文科)
一、选择题
1.B 2.A 3.D 4.D 5.A 6. D 7.B 8.B 9.D 10.C 11.D 12.A
二、填空题
13.5 14.2 15. 16.
17.解:(1)由题意及余弦定理,可得,
即,
所以.
因为,所以.
(2)由于,
所以,由正弦定理得,,
又,
所以的面积为.
18.解:(1)随机抽查1人,抽到满意的概率是,
抽到非常满意的女性的概率是;
(2)根据列联表,可得,
故有99.9%的把握认为性别和满意度有关.
19.(1)证明:在中,,
由余弦定理得.
所以,从而,
由勾股逆定理得,.
又因为平面平面,
所以,
由于平面平面,
所以平面,
又因为平面,
所以平面平面.
(2)解:取中点E,连接.
因为,所以.
又因为平面平面,平面平面,
所以平面,
故即为直线与平面所成的角,
因为,
所以,
所以,
则,
所以与平面所成角的正切值为.
20.解:(1)由题可知.
设点,
因为,即,
所以,
代入,得.
又因为,
所以,
所以抛物线C的方程为.
(2)设直线,
则消去y,可得,
满足,即,
设点,
则.
因为成等差数列,
,即,
即,即,
此时.
因为公差d满足,
且,
所以,即.
21.(1)由得由题意得:,
得得,
则,而切点在切线,
得,得,
令得,令得,
故函数在上单调递减,在上单调递增;
(2)由(1)知,且函数在上递减,
在上单调递增,而函数恰有两个零点,
则函数在区间各有一个零点,
由零点存在性定理得即,解得
∴
22.解:(1)因为圆C的参数方程为:(为参数),
所以圆C的普通方程为
又,则
所以圆C的极坐标方程为
(2)设,则有,解得
设,则有,解得
所以
【答案】①解:由题意,函数
因为,所以或或
解得,或或
所以的解集为R,
②解:由①可得当时,函数的最小值为
因为不等式对任意实数×恒成立,
所以,即,所以
故实数m的取值范围是
数学试卷(文科)
一、选择题
1.已知集合,则( )
A. B. C. D.
2.已知复数(其中i为虚数单位),则z的共轭复数为( )
A. B. C. D.
3.我国古代数学名著《数书九章》是南宋数学家秦九韶所著数学著作,书中共列算题81问,分为9类.全书采用问题集的形式,并不按数学方法来分类.题文也不只谈数学,还涉及自然现象和社会生活,成为了解当时社会政治和经济生活的重要参考文献.《数书九章》中有“米谷粒分”一题,现有类似的题:粮仓开仓收粮,粮农送来米1634石,验得米夹谷,抽样取米一把,数得254粒夹谷25粒,则这批米内夹谷约为( )
A.158石 B.159石 C.160石 D.161石
4.设、是两定点,,动点P满足,则动点P的轨迹是( )
A.双曲线 B.直线 C.线段 D.射线
5.在等比数列中,已知,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
6.已知,则a,b,c的大小关系为( )
A. B. C. D.
7.已知,则( )
A. B. C. D.
8.直线平分圆的周长,过点作圆C的一条切线,切点为Q,则( )
A.5 B.4 C.3 D.2
9.设x,y满足约束条件,则的范围是( )
A. B. C. D.
10.如图,在直三棱柱中,D为的中点,,则异面直线与所成的角为( )
A. B. C. D.
11.已知是双曲线的上、下焦点,点M是该双曲线的一条渐近线上的一点,并且以线段为直径的圆经过点M,则下列说法不正确的是( )
A.双曲线C的渐近线方程为 B.点M的横坐标为
C.的面积为 D.以为直径的圆的方程为
12.若函数在区间上有2个零点,则的取值范围是( )
A. B. C. D.
二、填空题
13.下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.
由图判断从_________日开始连续三天的空气质量指数方差最大.
14.已知向量与的夹角为行,,则__________.
15.词语“堑堵”、“阳马”、“鳖臑”等出现自中国数学名著《九章算术·商功》,是古代人对一些特殊锥体的称呼.在《九章算术·商功》中,把四个面都是直角三角形的四面体称为“鳖臑”.现有如图所示的“鳖臑”四面体,其中平面,则四面体的外接球的表面积为__________.
16.已知为等差数列的前n项和,,设,且数列的前n项和为,则使恒成立的实数的取值范围是__________.
三、解答题
17.在中,角A,B,C所对的边分别为a,b,c,已知.
(1)求A;
(2)若,求的面积.
18.为调查电影《长津湖》在国庆假期的上映满意度,抽取了男女各25人对这部电影的满意度进行调查,统计数据如表所示.
满意 非常满意 合度
男 18 7 25
女 6 19 25
合计 24 26 50
(1)如果随机抽查1人,那么抽到满意的概率是多少?抽到非常满意的女性的概率是多少?
(2)能否有99.9%的把握认为性别和满意度有关?
0.050 0.010 0.001
k 3.841 6.635 10.828
附:.
19.如图,在三棱锥中,平面.
(1)求证:平面平面;
(2)若,M是的中点,求与平面所成角的正切值.
20.已知抛物线的焦点为F,P是抛物线C上一点,且满足.
(1)求抛物线C的方程;
(2)已知斜率为2的直线l与抛物线C交于A,B两点,若成等差数列,求该数列的公差.
21.已知函数,且函数在处的切线为.
(1)求a,b的值并分析函数的单调性;
(2)若函数恰有两个零点,求实数m的取值范围.
(请考生在两题中任选一题作答,如果多作按所作第一题计分)
22-1选做题【选修4-4坐标系与参数方程】在直角坐标系中,圆C的参数方程为:(为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
①求圆C的极坐标方程;
②直线的极坐标方程是,射线:与圆C的交点为O,P,与直线l的交点为Q,求线的长.
22-2【选修4-5.不等式选讲】设函数.
①求的解集;
②若不等式对任意实数x恒成立,求实数m的取值范围.
临泽县2021-2022学年高二下学期期中考试
数学答案(文科)
一、选择题
1.B 2.A 3.D 4.D 5.A 6. D 7.B 8.B 9.D 10.C 11.D 12.A
二、填空题
13.5 14.2 15. 16.
17.解:(1)由题意及余弦定理,可得,
即,
所以.
因为,所以.
(2)由于,
所以,由正弦定理得,,
又,
所以的面积为.
18.解:(1)随机抽查1人,抽到满意的概率是,
抽到非常满意的女性的概率是;
(2)根据列联表,可得,
故有99.9%的把握认为性别和满意度有关.
19.(1)证明:在中,,
由余弦定理得.
所以,从而,
由勾股逆定理得,.
又因为平面平面,
所以,
由于平面平面,
所以平面,
又因为平面,
所以平面平面.
(2)解:取中点E,连接.
因为,所以.
又因为平面平面,平面平面,
所以平面,
故即为直线与平面所成的角,
因为,
所以,
所以,
则,
所以与平面所成角的正切值为.
20.解:(1)由题可知.
设点,
因为,即,
所以,
代入,得.
又因为,
所以,
所以抛物线C的方程为.
(2)设直线,
则消去y,可得,
满足,即,
设点,
则.
因为成等差数列,
,即,
即,即,
此时.
因为公差d满足,
且,
所以,即.
21.(1)由得由题意得:,
得得,
则,而切点在切线,
得,得,
令得,令得,
故函数在上单调递减,在上单调递增;
(2)由(1)知,且函数在上递减,
在上单调递增,而函数恰有两个零点,
则函数在区间各有一个零点,
由零点存在性定理得即,解得
∴
22.解:(1)因为圆C的参数方程为:(为参数),
所以圆C的普通方程为
又,则
所以圆C的极坐标方程为
(2)设,则有,解得
设,则有,解得
所以
【答案】①解:由题意,函数
因为,所以或或
解得,或或
所以的解集为R,
②解:由①可得当时,函数的最小值为
因为不等式对任意实数×恒成立,
所以,即,所以
故实数m的取值范围是
同课章节目录
