勾股定理(第2课时)
图片预览


文档简介
课件25张PPT。18.1 勾股定理 第2课时第十八章 勾股定理回 顾对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有
a2+b2=c2 直角三角形两直角边的平方和等于
斜边的平方.
abc几何语言:
∵在Rt△ABC中 ∠C=90°
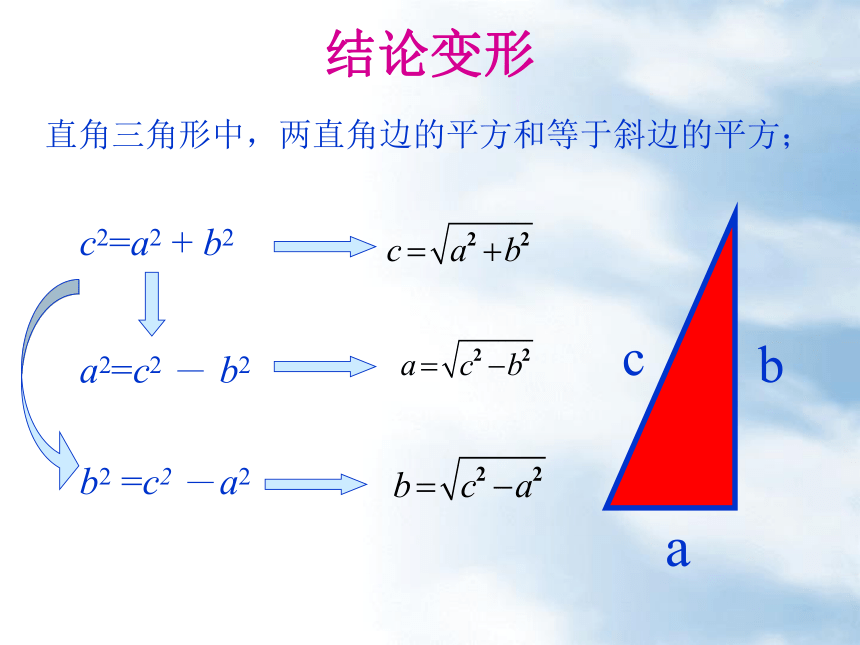
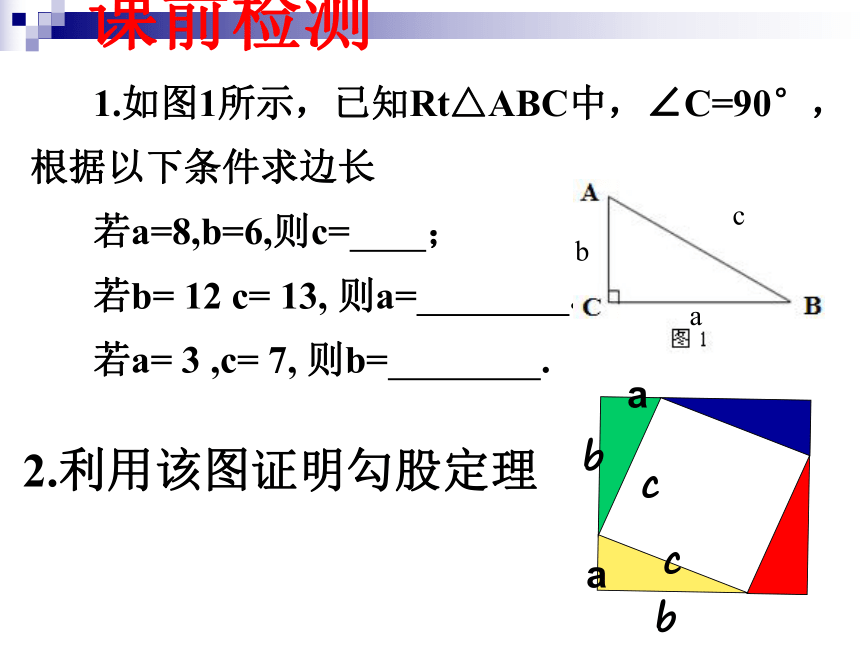
∴a2+b2=c2勾股定理:∟c2=a2 + b2a2=c2 - b2b2 =c2 -a2结论变形直角三角形中,两直角边的平方和等于斜边的平方; 情境引入1.如图1所示,已知Rt△ABC中,∠C=90°,根据以下条件求边长
若a=8,b=6,则c= ;
若b= 12 c= 13, 则a= .
若a= 3 ,c= 7, 则b= .
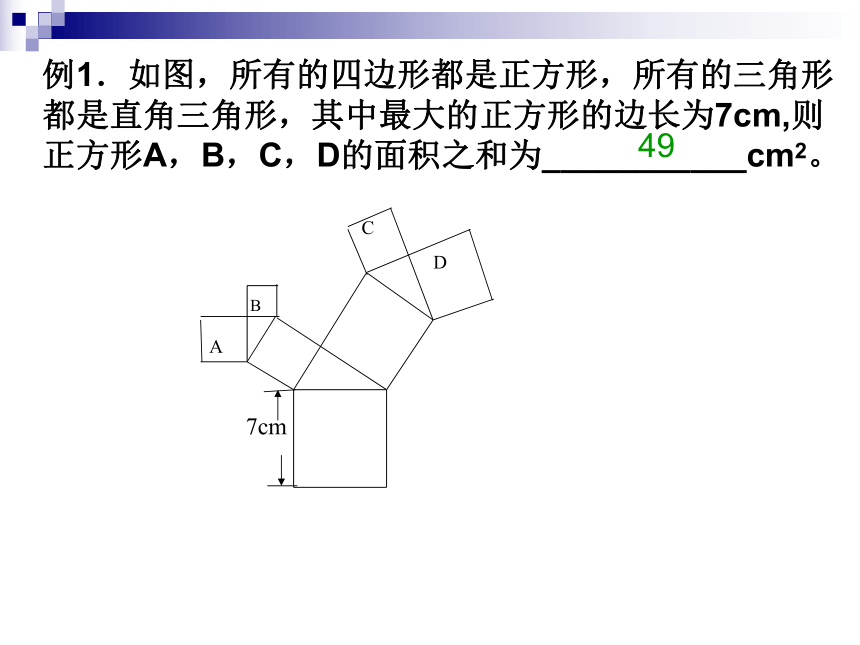
2.利用该图证明勾股定理课前检测例1.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
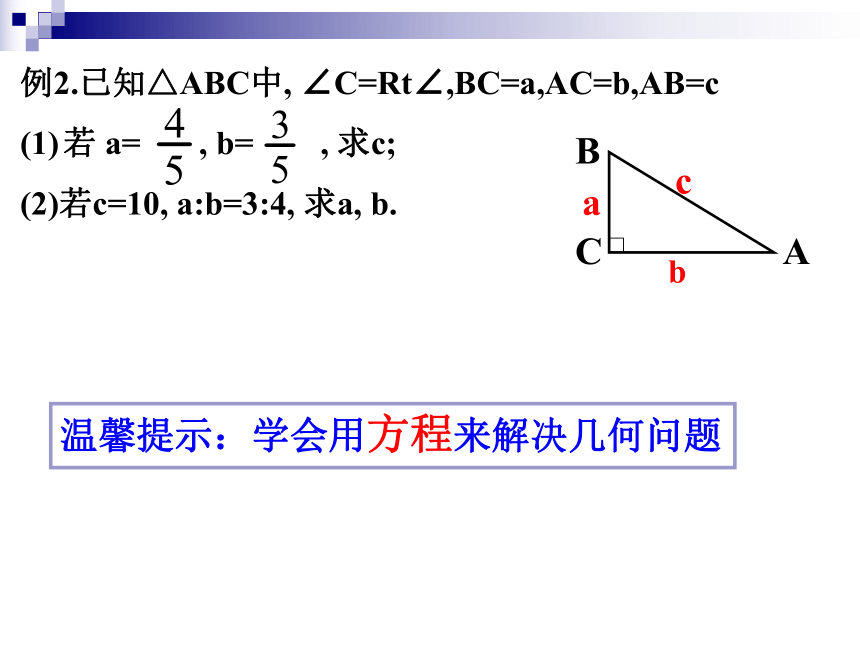
正方形A,B,C,D的面积之和为___________cm2。49例2.已知△ABC中, ∠C=Rt∠,BC=a,AC=b,AB=c
若 a= , b= , 求c;
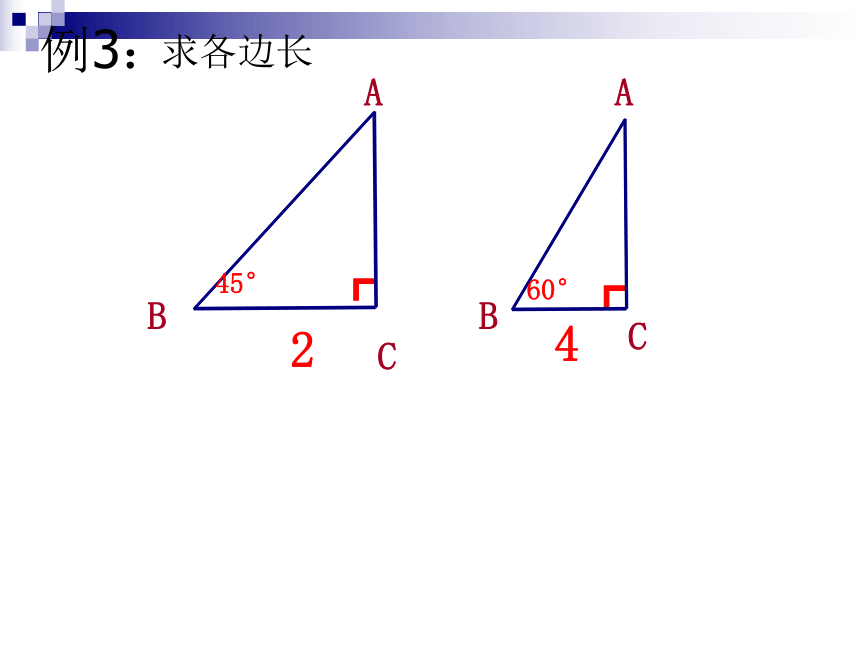
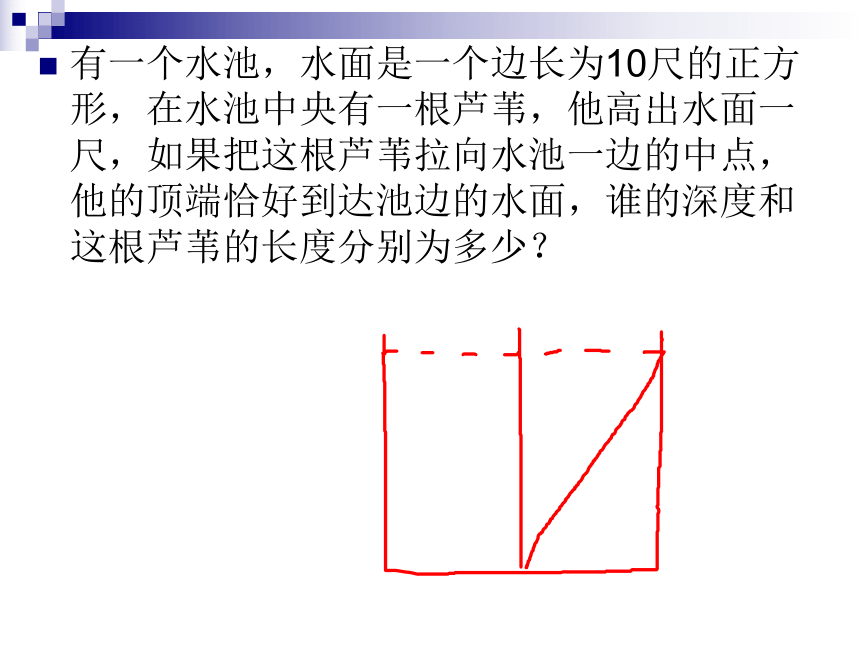
(2)若c=10, a:b=3:4, 求a, b.温馨提示:学会用方程来解决几何问题┏45°2BC┏4BCAA60°例3:求各边长有一个水池,水面是一个边长为10尺的正方形,在水池中央有一根芦苇,他高出水面一尺,如果把这根芦苇拉向水池一边的中点,他的顶端恰好到达池边的水面,谁的深度和这根芦苇的长度分别为多少? 某人拿着一根竹竿进一个宽3米的城门,她先横着拿不进去,又竖起来拿,结果竹竿比城门高3米,当他把竹竿斜着拿时,两端恰好顶着城门的对角,问竹竿长多少米?练习已知:△ABC,AB=AC=17,BC=16,则高
AD=_,S△ABC=___ 例4.如果一个直角三角形的两条边长分别是5厘米和12厘米,那么这个三角形的周长是多少厘米?在直角△ABC中, a=3, b=4, 则求c的值?ADBC34 已知∠ACB=90°,
CD⊥AB,AC=3,BC=4.
求CD的长.我来试一试∟C例5、 如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)图1中的x等于多少? 仔细想想!图2中的x、y、z等于多少? 想一想沿着图2继续画直角三角形,还能得到那些无理数? 图2中的图形的面积是多少? 算一算探究 数轴上的点有的表示有理数,有的
表示无理数,你能在数轴上画出
表示 的点吗?01LAC
练习:在数轴上作出表示的 点。20342B一个门框的尺寸如图所示,一块长3米,宽2米的薄木板能否从门框内通过1米2米门框能横着或竖着通过吗∵ 木板的宽2米大于1米
∴横着不能从门框通过∵ 木板的宽2米大于2米
∴竖着也不能从门框通过
探究1一个门框的尺寸如图所示,一块长3米,宽2.2米的薄木板能否从门框内通过1米1米那么斜着能否通过?大家试试看2.2米课中探究如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?在Rt△AOB中,
OB= = .
在Rt△COD中,
OD= = .
BD= .
梯子的顶端沿墙下滑0.5 m,梯子底端外移____一架云梯长25米,斜靠在面墙上,梯子顶端距地面的垂直高度为24米。 1, 梯子底端离墙多远? 2,如果梯子顶端下滑了4m,,那么梯子底部在水平方向也滑动了4m吗
3.当梯子的顶端下滑的距离与梯子的底部水平滑动的距离相等时,这时梯子的顶端距地面有多高?作业:70页7,8,10尝试应用1、求出下列直角三角形中未知的边.DA3、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE当堂达标1.一棵树因雪灾于A处折断,如图所示,测得树梢触地点B到树根C处的距离为4米,∠ABC约45°,树干AC垂直于地面,那么此树在未折断之前的高度约为 米
2.已知直角三角形的两直角边长分别为3cm和5cm,则第三边长为 ____cm第1题图当堂达标3. 有一个边长为1米正方形的洞口,想用一个圆形盖去盖住这个洞口,则圆形盖半径至少为 米.
4.长方形的一边长是5,对角线是13,则另一条边是 .
5.如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)第5题图
a2+b2=c2 直角三角形两直角边的平方和等于
斜边的平方.
abc几何语言:
∵在Rt△ABC中 ∠C=90°
∴a2+b2=c2勾股定理:∟c2=a2 + b2a2=c2 - b2b2 =c2 -a2结论变形直角三角形中,两直角边的平方和等于斜边的平方; 情境引入1.如图1所示,已知Rt△ABC中,∠C=90°,根据以下条件求边长
若a=8,b=6,则c= ;
若b= 12 c= 13, 则a= .
若a= 3 ,c= 7, 则b= .
2.利用该图证明勾股定理课前检测例1.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49例2.已知△ABC中, ∠C=Rt∠,BC=a,AC=b,AB=c
若 a= , b= , 求c;
(2)若c=10, a:b=3:4, 求a, b.温馨提示:学会用方程来解决几何问题┏45°2BC┏4BCAA60°例3:求各边长有一个水池,水面是一个边长为10尺的正方形,在水池中央有一根芦苇,他高出水面一尺,如果把这根芦苇拉向水池一边的中点,他的顶端恰好到达池边的水面,谁的深度和这根芦苇的长度分别为多少? 某人拿着一根竹竿进一个宽3米的城门,她先横着拿不进去,又竖起来拿,结果竹竿比城门高3米,当他把竹竿斜着拿时,两端恰好顶着城门的对角,问竹竿长多少米?练习已知:△ABC,AB=AC=17,BC=16,则高
AD=_,S△ABC=___ 例4.如果一个直角三角形的两条边长分别是5厘米和12厘米,那么这个三角形的周长是多少厘米?在直角△ABC中, a=3, b=4, 则求c的值?ADBC34 已知∠ACB=90°,
CD⊥AB,AC=3,BC=4.
求CD的长.我来试一试∟C例5、 如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)图1中的x等于多少? 仔细想想!图2中的x、y、z等于多少? 想一想沿着图2继续画直角三角形,还能得到那些无理数? 图2中的图形的面积是多少? 算一算探究 数轴上的点有的表示有理数,有的
表示无理数,你能在数轴上画出
表示 的点吗?01LAC
练习:在数轴上作出表示的 点。20342B一个门框的尺寸如图所示,一块长3米,宽2米的薄木板能否从门框内通过1米2米门框能横着或竖着通过吗∵ 木板的宽2米大于1米
∴横着不能从门框通过∵ 木板的宽2米大于2米
∴竖着也不能从门框通过
探究1一个门框的尺寸如图所示,一块长3米,宽2.2米的薄木板能否从门框内通过1米1米那么斜着能否通过?大家试试看2.2米课中探究如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?在Rt△AOB中,
OB= = .
在Rt△COD中,
OD= = .
BD= .
梯子的顶端沿墙下滑0.5 m,梯子底端外移____一架云梯长25米,斜靠在面墙上,梯子顶端距地面的垂直高度为24米。 1, 梯子底端离墙多远? 2,如果梯子顶端下滑了4m,,那么梯子底部在水平方向也滑动了4m吗
3.当梯子的顶端下滑的距离与梯子的底部水平滑动的距离相等时,这时梯子的顶端距地面有多高?作业:70页7,8,10尝试应用1、求出下列直角三角形中未知的边.DA3、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE当堂达标1.一棵树因雪灾于A处折断,如图所示,测得树梢触地点B到树根C处的距离为4米,∠ABC约45°,树干AC垂直于地面,那么此树在未折断之前的高度约为 米
2.已知直角三角形的两直角边长分别为3cm和5cm,则第三边长为 ____cm第1题图当堂达标3. 有一个边长为1米正方形的洞口,想用一个圆形盖去盖住这个洞口,则圆形盖半径至少为 米.
4.长方形的一边长是5,对角线是13,则另一条边是 .
5.如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)第5题图
