西南师大版六年级数学下册《圆柱和圆锥》单元评析课教案(含答案)
文档属性
| 名称 | 西南师大版六年级数学下册《圆柱和圆锥》单元评析课教案(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 47.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 17:11:11 | ||
图片预览

文档简介
《圆柱和圆锥》单元评析课教案
评析内容:《圆柱和圆锥》单元测试典型错题
课 型:评析课
教学目标:
1.通过辨析错因,夯实基础知识并及时反馈补救,强化基础知识过手过关,从而掌握各类题型的做题方法和做题技巧。
2.通过典型错题辨析,进一步培养学生分析问题、解决问题的能力,从而提高学生的思维能力。
3.通过总结提炼规律方法,进一步渗透数学思想方法,提升学生解题技能技巧。
教学重、难点:
通过辨析典型错题错因,让学生知道等底等高的圆柱、圆锥之间的关系;当把一个圆柱截成相等N个的圆柱体,切成的表面积比原来多了2N个底面积或者把几个底面积相等的圆柱底面连接成一个圆柱体表面积比原来减少了2N个底面积;运用圆柱和圆锥体积的计算公式解决等积问题;运用运动的观点,把不规则体转化成规则体,然后用圆柱和圆锥体积的公式解决问题。
教学准备:教师对本单元练习进行数据整理成表;学生完成单元练习;
教学过程
课前导学
课前请学生完成预学单:
1.改一改:请独立订正单元测试卷,请你圈出仍不会做的题目。
2.教一教:请四人小组内核对错题修改是否正确?会做的同学帮助辅导组内没有改对的同学。
3.说一说:互相交流自己摘录的典型错题的错误原因。
4.想一想:分析典型错题、统一小组意见准备汇报。
(大组长根据改错情况和在小组内初评情况给小组成员和小组加分。{加分标准根据《四人小组捆绑式评价细则》加分,并计入本次检测的第二项改错分里})
课堂导学
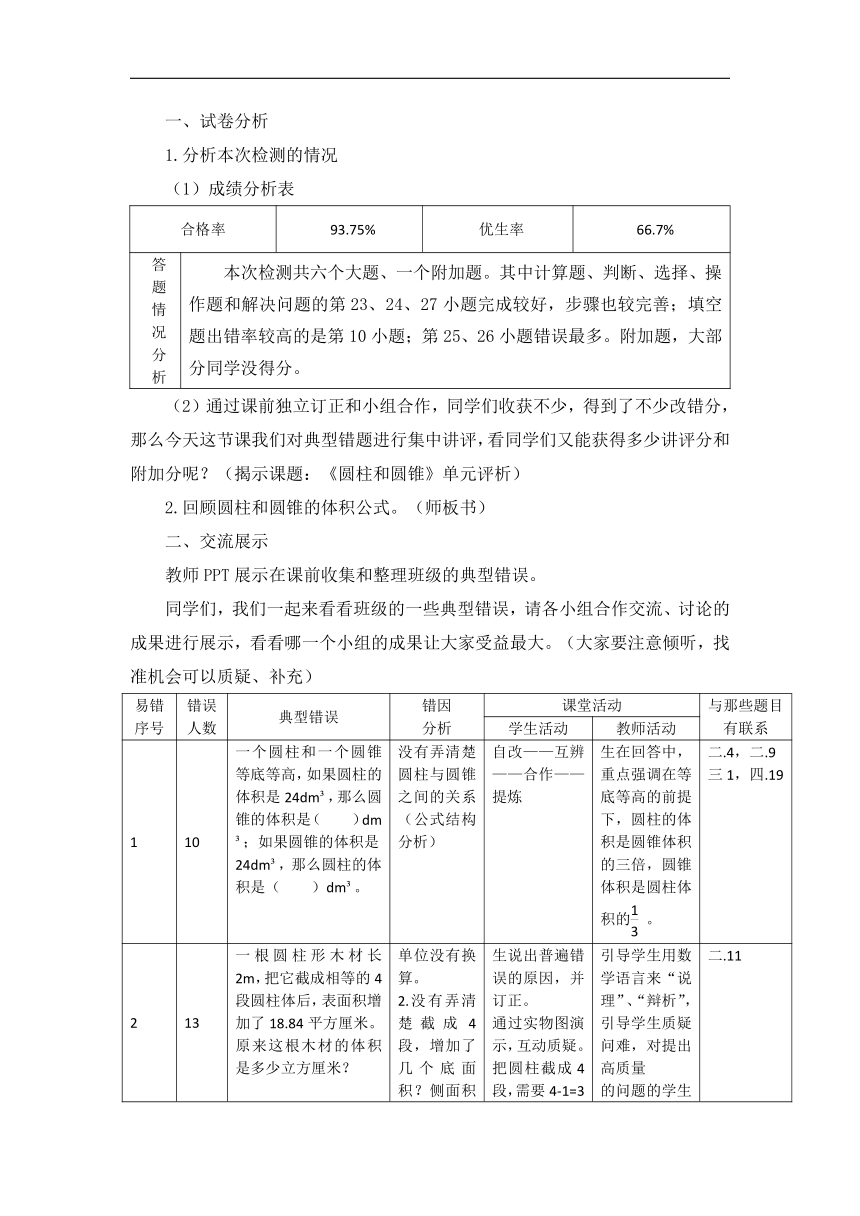
一、试卷分析
1.分析本次检测的情况
(1)成绩分析表
合格率 93.75% 优生率 66.7%
答题情况分析 本次检测共六个大题、一个附加题。其中计算题、判断、选择、操作题和解决问题的第23、24、27小题完成较好,步骤也较完善;填空题出错率较高的是第10小题;第25、26小题错误最多。附加题,大部分同学没得分。
(2)通过课前独立订正和小组合作,同学们收获不少,得到了不少改错分,那么今天这节课我们对典型错题进行集中讲评,看同学们又能获得多少讲评分和附加分呢?(揭示课题:《圆柱和圆锥》单元评析)
2.回顾圆柱和圆锥的体积公式。(师板书)
二、交流展示
教师PPT展示在课前收集和整理班级的典型错误。
同学们,我们一起来看看班级的一些典型错误,请各小组合作交流、讨论的成果进行展示,看看哪一个小组的成果让大家受益最大。(大家要注意倾听,找准机会可以质疑、补充)
易错序号 错误人数 典型错误 错因分析 课堂活动 与那些题目有联系
学生活动 教师活动
1 10 一个圆柱和一个圆锥等底等高,如果圆柱的体积是24dm ,那么圆锥的体积是( )dm ;如果圆锥的体积是24dm ,那么圆柱的体积是( )dm 。 没有弄清楚圆柱与圆锥之间的关系(公式结构分析) 自改——互辨——合作——提炼 生在回答中,重点强调在等底等高的前提下,圆柱的体积是圆锥体积的三倍,圆锥体积是圆柱体积的。 二.4,二.9三1,四.19
2 13 一根圆柱形木材长2m,把它截成相等的4段圆柱体后,表面积增加了18.84平方厘米。原来这根木材的体积是多少立方厘米? 单位没有换算。2.没有弄清楚截成4段,增加了几个底面积?侧面积没有变。 生说出普遍错误的原因,并订正。通过实物图演示,互动质疑。把圆柱截成4段,需要4-1=3次,每截1次表面积就增加2个圆柱的底面的面积,所以一共增加了3×2=6个圆柱的底面的面积,由此利用增加的表面积求出这个圆柱的底面积,再利用圆柱的体积公式即可求出木材的体积 引导学生用数学语言来“说理”、“辩析”, 引导学生质疑问难,对提出高质量的问题的学生及时肯定,把评价活动贯穿整个过程。 二.11
3 17 一个圆锥形容器,底面直径为6cm,高为8cm。先把这个容器装满水,然后将其中的水倒入一个底面半径是2cm的圆柱形容器中,则圆柱形容器里的水深是多少厘米? 圆柱体积公式、圆锥体积公式及计算 四人小组展示,分工负责各项汇报事宜,有主讲人和补充讲解人,还有负责板书的人。
根据已知圆锥的底面积直径,高可求出体积也就是圆柱容器内水的体积,知道了圆柱底面半径求出底面积,体积除以底面积就是水深。 1.圆锥容器内水的体积等于圆柱形容器内水的体积。2.引导学生用不同方法解决问题。3.在学生交流时,要关注学生所陈述的理由是否正确、到位,对不正确的理由要引导学生讨论、辩析,明确判断依据。 二.7四.20六.27
4 26 求如图所示图形的体积(单位:dm) 空间观念不强,没有弄清楚把不规则立体图形补成规则立体图形。 生汇报方法一:用两个一模一样的图形拼成一个底面直径为8分米,高(10+6)分米的圆柱体,这图形的体积就等于圆柱体体积的一半。方法二:先分成一个底面直径为8分米,高为6分米的圆柱体和一个不规则体,然后用第一个方法求体积。 关注学生汇报的计算过程,引导学生运用转化的数学思想,用补形法解决问题。 五.22
3、互助析疑
以小组为单位进行汇报,组间交流,对汇报过程中的遗漏和不足进行点评和补充。(根据讲评、表现、发言、质疑给小组和个人加讲评分,由大组长计入评价表)
四、过关练习。
1.两个等底等高的圆柱和圆锥,它们的体积之和是24立方厘米。其中圆锥的体积是( )立方厘米。
2.把两个完全一样的圆柱体拼成一个长为10厘米的圆柱体,表面积减少了25.12平方厘米,原来一个圆柱体的体积是( )立方厘米。
3.一个圆柱体铁块底面半径是3cm,高6cm,把它熔铸成底面半径是9cm的圆锥,圆锥的高是多少厘米?
4.以下图中直角三角形以其中一条直角边为轴旋转一周,可以得到一个什么立体图形,怎样旋转所得到的立体图形的体积大一些?
(学生对练习的完成和回答情况在附加分一栏加分)
五、课堂总结
1.通过这节课的讲评,你有哪些收获?和同学们交流一下。
2.各组员通过本节课的讲评,大组长汇报组员的最终得分情况(得分+改错分+讲评分+附加分=形成性评价总分),下来将对本单元检测情况再次进行分析。
六、收集整理:根据自己或班级的典型错题,搜集一些典型易错题或创编一道题,请写在导学单上。
七、板书设计
圆柱与圆锥单元评析
圆柱体积=底面积×高
圆锥体积=×底面积×高
等底等高:圆柱体积=3圆锥体积
八、教学反思:
8
10
6
4
3
评析内容:《圆柱和圆锥》单元测试典型错题
课 型:评析课
教学目标:
1.通过辨析错因,夯实基础知识并及时反馈补救,强化基础知识过手过关,从而掌握各类题型的做题方法和做题技巧。
2.通过典型错题辨析,进一步培养学生分析问题、解决问题的能力,从而提高学生的思维能力。
3.通过总结提炼规律方法,进一步渗透数学思想方法,提升学生解题技能技巧。
教学重、难点:
通过辨析典型错题错因,让学生知道等底等高的圆柱、圆锥之间的关系;当把一个圆柱截成相等N个的圆柱体,切成的表面积比原来多了2N个底面积或者把几个底面积相等的圆柱底面连接成一个圆柱体表面积比原来减少了2N个底面积;运用圆柱和圆锥体积的计算公式解决等积问题;运用运动的观点,把不规则体转化成规则体,然后用圆柱和圆锥体积的公式解决问题。
教学准备:教师对本单元练习进行数据整理成表;学生完成单元练习;
教学过程
课前导学
课前请学生完成预学单:
1.改一改:请独立订正单元测试卷,请你圈出仍不会做的题目。
2.教一教:请四人小组内核对错题修改是否正确?会做的同学帮助辅导组内没有改对的同学。
3.说一说:互相交流自己摘录的典型错题的错误原因。
4.想一想:分析典型错题、统一小组意见准备汇报。
(大组长根据改错情况和在小组内初评情况给小组成员和小组加分。{加分标准根据《四人小组捆绑式评价细则》加分,并计入本次检测的第二项改错分里})
课堂导学
一、试卷分析
1.分析本次检测的情况
(1)成绩分析表
合格率 93.75% 优生率 66.7%
答题情况分析 本次检测共六个大题、一个附加题。其中计算题、判断、选择、操作题和解决问题的第23、24、27小题完成较好,步骤也较完善;填空题出错率较高的是第10小题;第25、26小题错误最多。附加题,大部分同学没得分。
(2)通过课前独立订正和小组合作,同学们收获不少,得到了不少改错分,那么今天这节课我们对典型错题进行集中讲评,看同学们又能获得多少讲评分和附加分呢?(揭示课题:《圆柱和圆锥》单元评析)
2.回顾圆柱和圆锥的体积公式。(师板书)
二、交流展示
教师PPT展示在课前收集和整理班级的典型错误。
同学们,我们一起来看看班级的一些典型错误,请各小组合作交流、讨论的成果进行展示,看看哪一个小组的成果让大家受益最大。(大家要注意倾听,找准机会可以质疑、补充)
易错序号 错误人数 典型错误 错因分析 课堂活动 与那些题目有联系
学生活动 教师活动
1 10 一个圆柱和一个圆锥等底等高,如果圆柱的体积是24dm ,那么圆锥的体积是( )dm ;如果圆锥的体积是24dm ,那么圆柱的体积是( )dm 。 没有弄清楚圆柱与圆锥之间的关系(公式结构分析) 自改——互辨——合作——提炼 生在回答中,重点强调在等底等高的前提下,圆柱的体积是圆锥体积的三倍,圆锥体积是圆柱体积的。 二.4,二.9三1,四.19
2 13 一根圆柱形木材长2m,把它截成相等的4段圆柱体后,表面积增加了18.84平方厘米。原来这根木材的体积是多少立方厘米? 单位没有换算。2.没有弄清楚截成4段,增加了几个底面积?侧面积没有变。 生说出普遍错误的原因,并订正。通过实物图演示,互动质疑。把圆柱截成4段,需要4-1=3次,每截1次表面积就增加2个圆柱的底面的面积,所以一共增加了3×2=6个圆柱的底面的面积,由此利用增加的表面积求出这个圆柱的底面积,再利用圆柱的体积公式即可求出木材的体积 引导学生用数学语言来“说理”、“辩析”, 引导学生质疑问难,对提出高质量的问题的学生及时肯定,把评价活动贯穿整个过程。 二.11
3 17 一个圆锥形容器,底面直径为6cm,高为8cm。先把这个容器装满水,然后将其中的水倒入一个底面半径是2cm的圆柱形容器中,则圆柱形容器里的水深是多少厘米? 圆柱体积公式、圆锥体积公式及计算 四人小组展示,分工负责各项汇报事宜,有主讲人和补充讲解人,还有负责板书的人。
根据已知圆锥的底面积直径,高可求出体积也就是圆柱容器内水的体积,知道了圆柱底面半径求出底面积,体积除以底面积就是水深。 1.圆锥容器内水的体积等于圆柱形容器内水的体积。2.引导学生用不同方法解决问题。3.在学生交流时,要关注学生所陈述的理由是否正确、到位,对不正确的理由要引导学生讨论、辩析,明确判断依据。 二.7四.20六.27
4 26 求如图所示图形的体积(单位:dm) 空间观念不强,没有弄清楚把不规则立体图形补成规则立体图形。 生汇报方法一:用两个一模一样的图形拼成一个底面直径为8分米,高(10+6)分米的圆柱体,这图形的体积就等于圆柱体体积的一半。方法二:先分成一个底面直径为8分米,高为6分米的圆柱体和一个不规则体,然后用第一个方法求体积。 关注学生汇报的计算过程,引导学生运用转化的数学思想,用补形法解决问题。 五.22
3、互助析疑
以小组为单位进行汇报,组间交流,对汇报过程中的遗漏和不足进行点评和补充。(根据讲评、表现、发言、质疑给小组和个人加讲评分,由大组长计入评价表)
四、过关练习。
1.两个等底等高的圆柱和圆锥,它们的体积之和是24立方厘米。其中圆锥的体积是( )立方厘米。
2.把两个完全一样的圆柱体拼成一个长为10厘米的圆柱体,表面积减少了25.12平方厘米,原来一个圆柱体的体积是( )立方厘米。
3.一个圆柱体铁块底面半径是3cm,高6cm,把它熔铸成底面半径是9cm的圆锥,圆锥的高是多少厘米?
4.以下图中直角三角形以其中一条直角边为轴旋转一周,可以得到一个什么立体图形,怎样旋转所得到的立体图形的体积大一些?
(学生对练习的完成和回答情况在附加分一栏加分)
五、课堂总结
1.通过这节课的讲评,你有哪些收获?和同学们交流一下。
2.各组员通过本节课的讲评,大组长汇报组员的最终得分情况(得分+改错分+讲评分+附加分=形成性评价总分),下来将对本单元检测情况再次进行分析。
六、收集整理:根据自己或班级的典型错题,搜集一些典型易错题或创编一道题,请写在导学单上。
七、板书设计
圆柱与圆锥单元评析
圆柱体积=底面积×高
圆锥体积=×底面积×高
等底等高:圆柱体积=3圆锥体积
八、教学反思:
8
10
6
4
3
