华师大版数学八下 20.2.2 平均数、中位数和众数的选用 课件(共19张)
文档属性
| 名称 | 华师大版数学八下 20.2.2 平均数、中位数和众数的选用 课件(共19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 909.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-23 19:10:06 | ||
图片预览





文档简介
(共19张PPT)
华东师大版 八年级下册
20.2 数据的集中趋势
2.平均数、中位数和众数的选用
新课导入
平均数反映一组数据的( );中位数反映一组数据的( );众数反映一组数据的( ).
A.多数水平 B.平均水平 C.中等水平
B
C
A
10 20 70 40 50 90 50 40 50 40
分别求下面一组数据的众数、中位数与平均数:
解:平均数是45;中位数是45;众数是40和50.
我们已经知道,平均数、中位数和众数都是用来代表一组数据的,而且,它们相互之间可以相等也可以不相等,没有固定的大小关系.当它们不全相等时,就产生了如何选用才恰当的问题.
八年级某班级教室里,三个同学正在为谁的数学成绩最好而争论,他们五次数学成绩分别是:
问题
小华:62、94、95、98、98
小明:62、62、98、99、100
小丽:40、62、85、99、99
他们都认为自己的成绩比另两位同学好,你认为呢?
新课探究
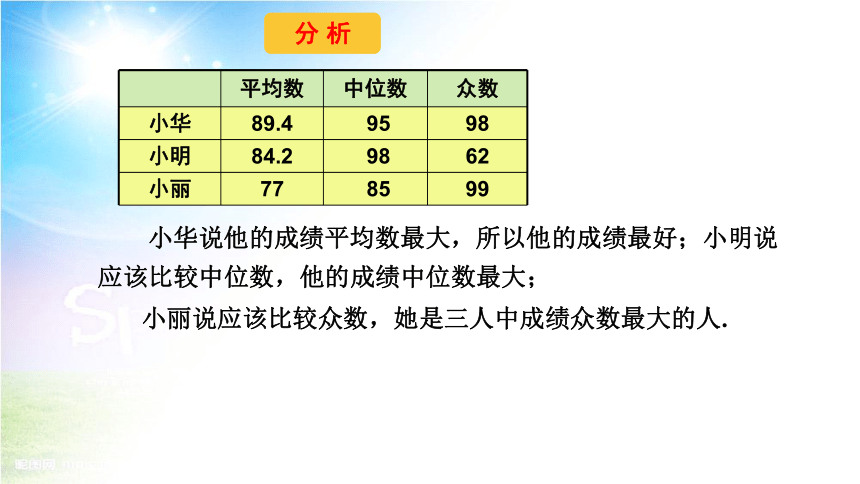
平均数 中位数 众数
小华 89.4 95 98
小明 84.2 98 62
小丽 77 85 99
分 析
小华说他的成绩平均数最大,所以他的成绩最好;小明说应该比较中位数,他的成绩中位数最大;
小丽说应该比较众数,她是三人中成绩众数最大的人.
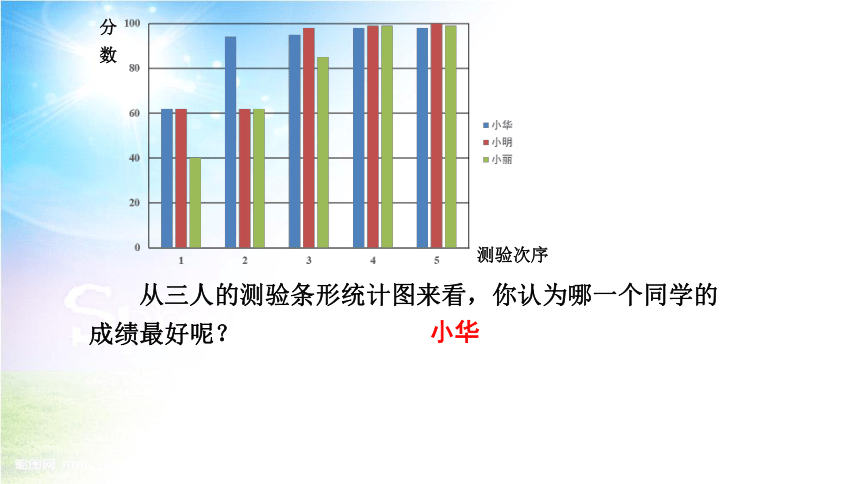
从三人的测验条形统计图来看,你认为哪一个同学的成绩最好呢?
分数
测验次序
小华
思 考
高一级学校录取新生主要依据是考生的总分,这与平均数,中位数和众数中的哪个量关系最大
总分与平均数关系最大;一组数据中任何一个数据的变化都会引起平均数发生变化,所以评价成绩一般用平均数.
问题
随着汽车的日益普及,越来越多的城市发生了令人头痛的交通堵塞问题.你认为用过往车辆一天车速的平均数衡量某条交通主干道的路况合适吗?
人们上、下班两个时段是一天中道路最繁忙的时候,其它时段车流量明显减少,因此,如果用一天车速的平均数来衡量道路的路况,那么上、下班交通堵塞的问题就给掩盖了.所以,应该按道路繁忙的不同程度,将一天分为几个时段分别计算车速较为合理.
分 析
平均数、中位数和众数各有其长,也各有其短,下面的几个例子也许能让你对它们有更深入的了解.
(1)草地上有六个人在玩游戏,他们的平均年龄是15岁,请猜想一下是怎样的年龄的六个人在玩游戏?
通常人们会想象是一群中学生在玩游戏,但是,如果是一个65岁的大娘领着5个5岁的孩子在玩游戏也是有可能的.
(2)为筹备班级的新年晚会,班长对全班同学爱吃的几种水果作了民意调查. 最终买什么水果,该由调查的平均数,众数还是中位数决定呢?
显然是由众数决定好,因为它代表了全班多数同学的意愿.
练 习
1、检验某厂生产的手表质量时,检查人员随机抽取了 10 块手表,在下表中记下了每块手表的走时误差(正数表示比标准时间快,负数表示比标准时间慢),你认为用这 10 块手表误差的平均数来衡量这 10 块手表的精度合适吗
手 表 序 号 1 2 3 4 5 6 7 8 9 10
日走时误差(秒) -2 0 1 -3 -1 0 2 4 -3 2
解:不合适,虽然这 10 块手表误差的平均数是 0,但从测得的数据看,10块手表中只有2块不快不慢,显然不能认为这些手表有很高的精度.
2、5名学生在一次考试中的得分分别是: 18, 73, 78, 90, 100,考分为 73 的学生是在平均分之上还是之下?你认为他在 5 个人中考分属“中上”水平吗?
这5 位同学的平均分是 71.8 分,考分为 73的同学是在平均分之上,但他的分数在五人中排倒数第二,不能算是“中上水平”.
练 习
3、 9名学生的鞋号由小到大是:20, 21, 21, 22, 22, 22, 22, 23, 23,这组数据的平均数、中位数和众数中哪个指标是鞋厂最不感兴趣的?哪个指标是鞋厂最兴趣的?
鞋厂最不感兴趣的指标是平均数,因为有可能没有一个学生的鞋号等于这个平均数.最感兴趣的指标是众数,因为它表明工厂应该生产最多这一鞋号的鞋.
练 均数、中位数、众数的联系与区别
联系:都反映了一组数据的集中趋势
平均数能充分利用各数据,在实际中较为常用,但受极端值影响,任何一个数据的变动都会引起平均数的变动;
归纳总结
中位数仅与数据的排列位置有关,不受极端值或某些数据的变动;
众数主要研究各数据出现的次数,其大小只与这组数据中的某些数据有关.
当堂练习
1、为了了解某班学生每周做家务劳动的时间,某综合
实践活动小组对该班50名学生进行了调查,有关数据如下表,
根据表中的数据,回答下列问题:
每周做家务的 时间(小时) 0 1 1.5 2 2.5 3 3.5 4
人数(人) 2 2 6 8 12 13 4 3
(1)该班学生每周做家务劳动的平均时间是多少小时?
(2)这组数据的中位数、众数分别是多少?
(3)请你根据(1)、(2)的结果,用一句话谈谈自己的感受.
解:(1)该班学生每周做家务劳动的平均时间为2.44小时
(2)这组数据的中位数是2.5小时,众数是3小时
(3)只要叙述内容与上述数据有关或与做家务劳动有关,
并且态度积极即可
当堂练习
2、三个生产日光灯管的厂家在广告中宣称,他们生产的日光灯管在正常情况下,灯管的使用寿命为12个月.工商部门为了检查他们宣传的真实性,从三个厂家各抽取11只日光灯管进行检测,灯管的使用寿命(单位:月)如下:
甲厂 7 8 9 9 9 11 13 14 16 17 19
乙厂 7 7 9 9 10 10 12 12 12 13 14
丙厂 7 7 8 8 8 12 13 14 15 16 17
(1)这三个厂家的广告,分别利用了统计中的哪一个特征数(平均数、中位数、众数)进行宣传;
(2)如果三种产品的售价一样,作为顾客的你选购哪个厂家的产品?请说明理由.
当堂练习
解:(1)甲厂的平均数=(7+8+9+9+9+11+13+14
+16+17+19)÷11=12,
∴甲厂的广告利用了统计中的平均数;由于乙厂数据中
12有3次,是众数,故乙厂的广告利用了统计中的众数;
丙厂数据中的中位数是12,故丙厂的广告利用了统计中
的中位数
(2)选用甲厂的产品,因为它的平均数较真实的反映灯管
的使用寿命;或选用丙厂的产品,因为丙厂有一半以上
的灯管使用寿命超过12个月
当堂练习
3、6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A,B,C,D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级一班和二班的成绩整理并绘制成
统计图:
根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整;
当堂练习
(2)写出下表中a,b,c的值:
平均数(分) 中位数(分) 众数(分)
一班 a b 90
二班 87.6 80 c
(3)请从以下给出的三个方面中任选一个对这次竞赛成绩
的结果进行分析:
①从平均数和中位数方面比较一班和二班的成绩;
②从平均数和众数方面比较一班和二班的成绩;
③从B级以上(包括B级)的人数方面来比较一班和二班的成绩.
当堂练习
解:(1)25-6-12-5=2(人),补图略
(2)a=87.6,b=90,c=100
(3)①一班和二班平均数相等,一班的中位数大于二班
的中位数,故一班的成绩好于二班;
②一班和二班平均数相等,一班的众数小于二班的众
数,故二班的成绩好于一班;
③B级以上(包括B级)一班18人,二班12人,故一班的
成绩好于二班
华东师大版 八年级下册
20.2 数据的集中趋势
2.平均数、中位数和众数的选用
新课导入
平均数反映一组数据的( );中位数反映一组数据的( );众数反映一组数据的( ).
A.多数水平 B.平均水平 C.中等水平
B
C
A
10 20 70 40 50 90 50 40 50 40
分别求下面一组数据的众数、中位数与平均数:
解:平均数是45;中位数是45;众数是40和50.
我们已经知道,平均数、中位数和众数都是用来代表一组数据的,而且,它们相互之间可以相等也可以不相等,没有固定的大小关系.当它们不全相等时,就产生了如何选用才恰当的问题.
八年级某班级教室里,三个同学正在为谁的数学成绩最好而争论,他们五次数学成绩分别是:
问题
小华:62、94、95、98、98
小明:62、62、98、99、100
小丽:40、62、85、99、99
他们都认为自己的成绩比另两位同学好,你认为呢?
新课探究
平均数 中位数 众数
小华 89.4 95 98
小明 84.2 98 62
小丽 77 85 99
分 析
小华说他的成绩平均数最大,所以他的成绩最好;小明说应该比较中位数,他的成绩中位数最大;
小丽说应该比较众数,她是三人中成绩众数最大的人.
从三人的测验条形统计图来看,你认为哪一个同学的成绩最好呢?
分数
测验次序
小华
思 考
高一级学校录取新生主要依据是考生的总分,这与平均数,中位数和众数中的哪个量关系最大
总分与平均数关系最大;一组数据中任何一个数据的变化都会引起平均数发生变化,所以评价成绩一般用平均数.
问题
随着汽车的日益普及,越来越多的城市发生了令人头痛的交通堵塞问题.你认为用过往车辆一天车速的平均数衡量某条交通主干道的路况合适吗?
人们上、下班两个时段是一天中道路最繁忙的时候,其它时段车流量明显减少,因此,如果用一天车速的平均数来衡量道路的路况,那么上、下班交通堵塞的问题就给掩盖了.所以,应该按道路繁忙的不同程度,将一天分为几个时段分别计算车速较为合理.
分 析
平均数、中位数和众数各有其长,也各有其短,下面的几个例子也许能让你对它们有更深入的了解.
(1)草地上有六个人在玩游戏,他们的平均年龄是15岁,请猜想一下是怎样的年龄的六个人在玩游戏?
通常人们会想象是一群中学生在玩游戏,但是,如果是一个65岁的大娘领着5个5岁的孩子在玩游戏也是有可能的.
(2)为筹备班级的新年晚会,班长对全班同学爱吃的几种水果作了民意调查. 最终买什么水果,该由调查的平均数,众数还是中位数决定呢?
显然是由众数决定好,因为它代表了全班多数同学的意愿.
练 习
1、检验某厂生产的手表质量时,检查人员随机抽取了 10 块手表,在下表中记下了每块手表的走时误差(正数表示比标准时间快,负数表示比标准时间慢),你认为用这 10 块手表误差的平均数来衡量这 10 块手表的精度合适吗
手 表 序 号 1 2 3 4 5 6 7 8 9 10
日走时误差(秒) -2 0 1 -3 -1 0 2 4 -3 2
解:不合适,虽然这 10 块手表误差的平均数是 0,但从测得的数据看,10块手表中只有2块不快不慢,显然不能认为这些手表有很高的精度.
2、5名学生在一次考试中的得分分别是: 18, 73, 78, 90, 100,考分为 73 的学生是在平均分之上还是之下?你认为他在 5 个人中考分属“中上”水平吗?
这5 位同学的平均分是 71.8 分,考分为 73的同学是在平均分之上,但他的分数在五人中排倒数第二,不能算是“中上水平”.
练 习
3、 9名学生的鞋号由小到大是:20, 21, 21, 22, 22, 22, 22, 23, 23,这组数据的平均数、中位数和众数中哪个指标是鞋厂最不感兴趣的?哪个指标是鞋厂最兴趣的?
鞋厂最不感兴趣的指标是平均数,因为有可能没有一个学生的鞋号等于这个平均数.最感兴趣的指标是众数,因为它表明工厂应该生产最多这一鞋号的鞋.
练 均数、中位数、众数的联系与区别
联系:都反映了一组数据的集中趋势
平均数能充分利用各数据,在实际中较为常用,但受极端值影响,任何一个数据的变动都会引起平均数的变动;
归纳总结
中位数仅与数据的排列位置有关,不受极端值或某些数据的变动;
众数主要研究各数据出现的次数,其大小只与这组数据中的某些数据有关.
当堂练习
1、为了了解某班学生每周做家务劳动的时间,某综合
实践活动小组对该班50名学生进行了调查,有关数据如下表,
根据表中的数据,回答下列问题:
每周做家务的 时间(小时) 0 1 1.5 2 2.5 3 3.5 4
人数(人) 2 2 6 8 12 13 4 3
(1)该班学生每周做家务劳动的平均时间是多少小时?
(2)这组数据的中位数、众数分别是多少?
(3)请你根据(1)、(2)的结果,用一句话谈谈自己的感受.
解:(1)该班学生每周做家务劳动的平均时间为2.44小时
(2)这组数据的中位数是2.5小时,众数是3小时
(3)只要叙述内容与上述数据有关或与做家务劳动有关,
并且态度积极即可
当堂练习
2、三个生产日光灯管的厂家在广告中宣称,他们生产的日光灯管在正常情况下,灯管的使用寿命为12个月.工商部门为了检查他们宣传的真实性,从三个厂家各抽取11只日光灯管进行检测,灯管的使用寿命(单位:月)如下:
甲厂 7 8 9 9 9 11 13 14 16 17 19
乙厂 7 7 9 9 10 10 12 12 12 13 14
丙厂 7 7 8 8 8 12 13 14 15 16 17
(1)这三个厂家的广告,分别利用了统计中的哪一个特征数(平均数、中位数、众数)进行宣传;
(2)如果三种产品的售价一样,作为顾客的你选购哪个厂家的产品?请说明理由.
当堂练习
解:(1)甲厂的平均数=(7+8+9+9+9+11+13+14
+16+17+19)÷11=12,
∴甲厂的广告利用了统计中的平均数;由于乙厂数据中
12有3次,是众数,故乙厂的广告利用了统计中的众数;
丙厂数据中的中位数是12,故丙厂的广告利用了统计中
的中位数
(2)选用甲厂的产品,因为它的平均数较真实的反映灯管
的使用寿命;或选用丙厂的产品,因为丙厂有一半以上
的灯管使用寿命超过12个月
当堂练习
3、6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A,B,C,D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级一班和二班的成绩整理并绘制成
统计图:
根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整;
当堂练习
(2)写出下表中a,b,c的值:
平均数(分) 中位数(分) 众数(分)
一班 a b 90
二班 87.6 80 c
(3)请从以下给出的三个方面中任选一个对这次竞赛成绩
的结果进行分析:
①从平均数和中位数方面比较一班和二班的成绩;
②从平均数和众数方面比较一班和二班的成绩;
③从B级以上(包括B级)的人数方面来比较一班和二班的成绩.
当堂练习
解:(1)25-6-12-5=2(人),补图略
(2)a=87.6,b=90,c=100
(3)①一班和二班平均数相等,一班的中位数大于二班
的中位数,故一班的成绩好于二班;
②一班和二班平均数相等,一班的众数小于二班的众
数,故二班的成绩好于一班;
③B级以上(包括B级)一班18人,二班12人,故一班的
成绩好于二班
