华师大版数学八下 20.3.1 方差 课件(20张PPT)
文档属性
| 名称 | 华师大版数学八下 20.3.1 方差 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 802.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-23 11:34:42 | ||
图片预览




文档简介
(共20张PPT)
华东师大版 八年级下册
20.3 数据的离散程度
1.方差
复习回忆:
2.求下列数据的平均数、众数和中位数
450,420,500,450,500,600,500,480,480,500。
1.平均数、众数、中位数的意义?
平均数:所有数据之和/数据个数.
众数:数据中出现最多的数值.
中位数:将数据从小到大排列处在中间位置的那个值.数据是偶数个时取两个数的平均数作为中位数.
488
500
490
新课探究
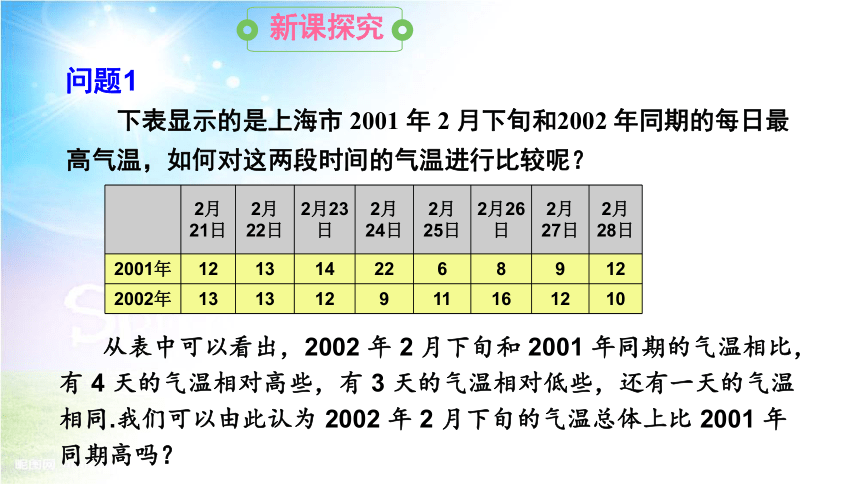
下表显示的是上海市 2001 年 2 月下旬和2002 年同期的每日最高气温,如何对这两段时间的气温进行比较呢?
问题1
2月21日 2月22日 2月23日 2月24日 2月25日 2月26日 2月27日 2月28日
2001年 12 13 14 22 6 8 9 12
2002年 13 13 12 9 11 16 12 10
从表中可以看出,2002 年 2 月下旬和 2001 年同期的气温相比,有 4 天的气温相对高些,有 3 天的气温相对低些,还有一天的气温相同.我们可以由此认为 2002 年 2 月下旬的气温总体上比 2001 年同期高吗?
新课探究
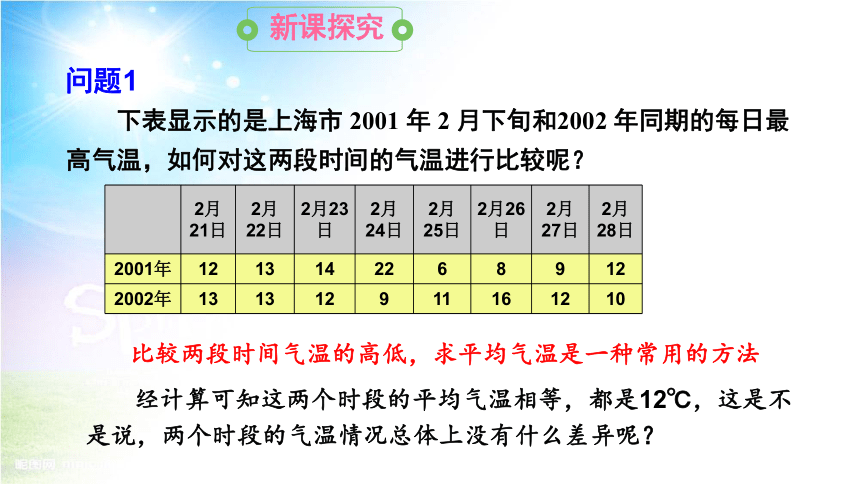
下表显示的是上海市 2001 年 2 月下旬和2002 年同期的每日最高气温,如何对这两段时间的气温进行比较呢?
问题1
2月21日 2月22日 2月23日 2月24日 2月25日 2月26日 2月27日 2月28日
2001年 12 13 14 22 6 8 9 12
2002年 13 13 12 9 11 16 12 10
比较两段时间气温的高低,求平均气温是一种常用的方法
经计算可知这两个时段的平均气温相等,都是12℃,这是不是说,两个时段的气温情况总体上没有什么差异呢?
21日
22日
23日
24日
25日
26日
27日
28日
21日
22日
23日
24日
25日
26日
27日
28日
气温(℃)
气温(℃)
(a)2001年2月下旬
(b)2002年2月下旬
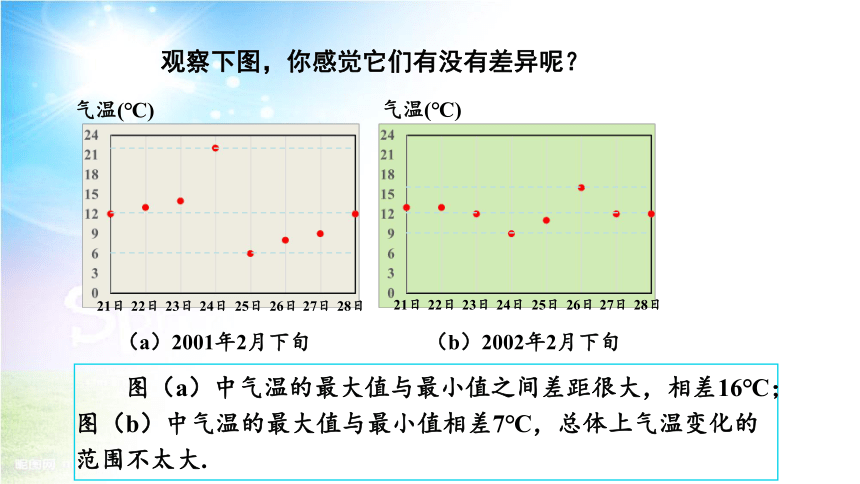
观察下图,你感觉它们有没有差异呢?
通过观察,我们可以发现:图(a)中的点波动范围比较大——从6℃到22℃,图(b)中的点波动范围比较小——从9℃到16℃.
21日
22日
23日
24日
25日
26日
27日
28日
21日
22日
23日
24日
25日
26日
27日
28日
气温(℃)
气温(℃)
(a)2001年2月下旬
(b)2002年2月下旬
观察下图,你感觉它们有没有差异呢?
图(a)中气温的最大值与最小值之间差距很大,相差16℃;图(b)中气温的最大值与最小值相差7℃,总体上气温变化的范围不太大.
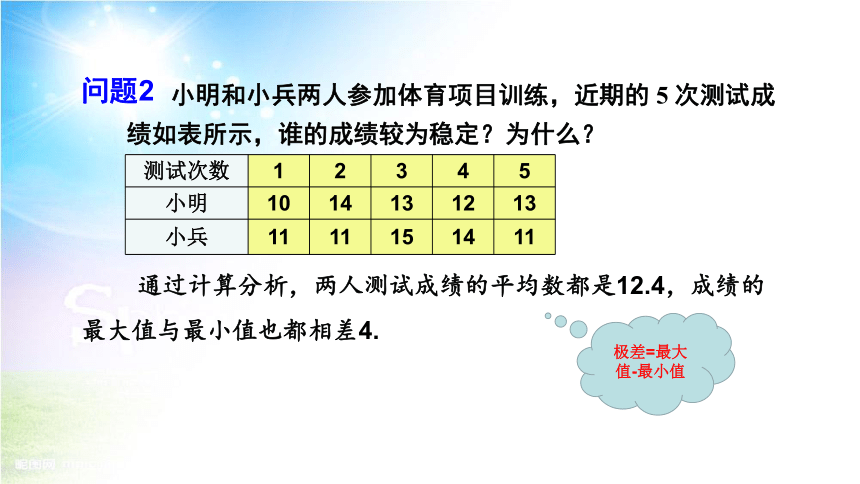
问题2
小明和小兵两人参加体育项目训练,近期的 5 次测试成绩如表所示,谁的成绩较为稳定?为什么?
测试次数 1 2 3 4 5
小明 10 14 13 12 13
小兵 11 11 15 14 11
通过计算分析,两人测试成绩的平均数都是12.4,成绩的最大值与最小值也都相差4.
极差=最大值-最小值
16
14
12
10
8
6
4
2
0
1
2
3
4
5
体育项目测试成绩图
从图中我们可以看到:相比之下,小明的成绩大部分集中在平均数附近,而小兵的成绩与其平均数的离散程度略大.
通常,如果一组数与其平均数的离散程度较小,我们就说它比较稳定.
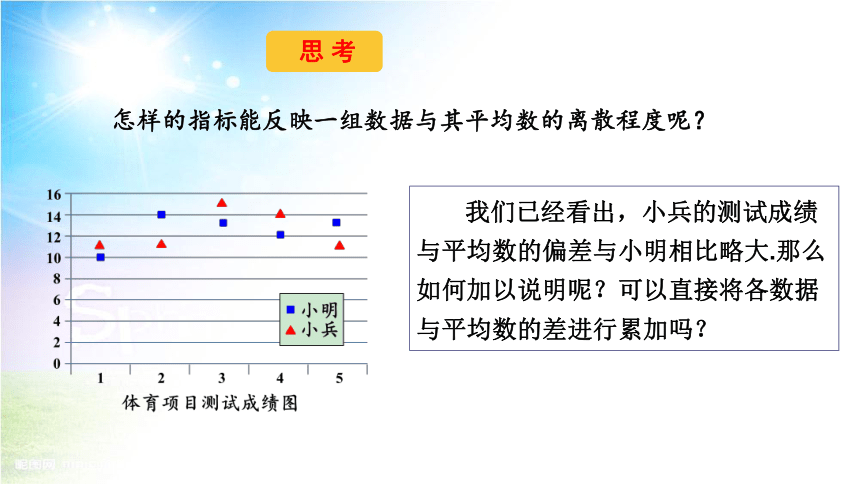
思 考
怎样的指标能反映一组数据与其平均数的离散程度呢?
我们已经看出,小兵的测试成绩与平均数的偏差与小明相比略大.那么如何加以说明呢?可以直接将各数据与平均数的差进行累加吗?
1 2 3 4 5 求和
小明 每次测试成绩 10 14 13 12 13
每次成绩-平均成绩
小兵 每次测试成绩 11 11 15 14 11
每次成绩-平均成绩
在下表中写出你的计算结果.
-2.4
1.6
0.6
-0.4
0.6
0.6
-1.4
-1.4
2.6
1.6
-1.4
0
依据最后求和的结果可以比较两组数据围绕其平均数的波动情况吗?
如果不行,请你提出一个可行的方案,在下表中写上新的计算方案.
思 考
如果一共进行了7次测试,小明因故缺席了2次,怎样比较谁的成绩更稳定?
1 2 3 4 5 6 7 平均
小明 每次测试成绩 10 14 13 缺席 12 缺席 13
小兵 每次测试成绩 11 11 15 14 11 14 11
(每次成绩-平均成绩)2
5.76
2.56
0.36
0.16
0.36
1.84
(每次成绩-平均成绩)2
1.96
1.96
6.76
2.56
1.96
2.56
1.96
2.82
方 差
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况,这个结果称为方差.
我们通常用 s2 表示一组数据的方差,用 表示一组数据的平均数,x1,x2,…,xn表示各个数据,方差的计算公式:
方差主要反映整组数据的波动情况,是反映一组数据与其平均值离散程度的一个重要指标,每个数年据的变化都将影响方差的结果,是一个对整组数据波动情况比较敏感的指标.
在实际使用时,往往计算一组数据的方差,来衡量一组数据的波动大小.
测试次数 1 2 3 4 5
小明 10 14 13 12 13
小兵 11 11 15 14 11
上表中,小明和小兵5次测试成绩的方差的计算式是
计算可得:
小明 5 次测试成绩的方差为_______,
小兵 5 次测试成绩的方差为_______.
计算结果是否是小明的成绩比较稳定呢?
1.84
3.04
归纳总结
方差是用来衡量一组数据的波动大小的特征量
方差越大,数据的波动越大;方差越小,数据的波动越小,通过比较方差的大小来判断数据的稳定性.
随堂演练
1. 计算下列两组数据的平均数和方差:
A 组:0, 10, 5, 5, 5, 5, 5, 5, 5, 5;
B 组:4, 6, 3, 7, 2, 8, 1, 9, 5, 5.
解:A 组的平均数为 5,方差为 5.
B 组的平均数为 5,方差为 6.
2. 甲、乙两台机床生产同种零件,10天出的次品个数分别是:
甲:0,1,0,2,2,0,3,1,2,4
乙:2,3,1,2,0,2,1,1,2,1
分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好?
解:
s2甲>s2乙
∴乙台机床的性能较好
课堂小结
方差是用来衡量一组数据的波动大小的特征量
方差越大,数据的波动越大;方差越小,数据的波动越小,通过比较方差的大小来判断数据的稳定性.
方法小结:
求方差
先平均,再求差,然后平方,最后再平均.
1、已知一组数据-3,x,-2,3,1,6的中位数为1,则其方差为____.
2、小李和小林练习射箭,射完10箭后两人的成绩如图所示,通常新手的成绩不太稳定,根据图中的信息,估计这两人中的新手是 _________.
小李
9
5、某校举行健美操比赛,甲、乙两个班选20名学生参加比赛,两个班参赛学生的平均身高都是1.65米,其方差分别是s甲2=1.9,s乙2=2.4,则参赛学生身高比较整齐的班级是( )
A.甲班 B.乙班
C.同样整齐 D.无法确定
3、要判断小强同学的数学考试成绩是否稳定,那么需要知道他最近几次数学考试成绩的( )
A.方差 B.众数 C.平均数 D.中位数
4、数据0,-1,6,1,x的众数为-1,则这组数据的方差是( )
A
B
A
A
华东师大版 八年级下册
20.3 数据的离散程度
1.方差
复习回忆:
2.求下列数据的平均数、众数和中位数
450,420,500,450,500,600,500,480,480,500。
1.平均数、众数、中位数的意义?
平均数:所有数据之和/数据个数.
众数:数据中出现最多的数值.
中位数:将数据从小到大排列处在中间位置的那个值.数据是偶数个时取两个数的平均数作为中位数.
488
500
490
新课探究
下表显示的是上海市 2001 年 2 月下旬和2002 年同期的每日最高气温,如何对这两段时间的气温进行比较呢?
问题1
2月21日 2月22日 2月23日 2月24日 2月25日 2月26日 2月27日 2月28日
2001年 12 13 14 22 6 8 9 12
2002年 13 13 12 9 11 16 12 10
从表中可以看出,2002 年 2 月下旬和 2001 年同期的气温相比,有 4 天的气温相对高些,有 3 天的气温相对低些,还有一天的气温相同.我们可以由此认为 2002 年 2 月下旬的气温总体上比 2001 年同期高吗?
新课探究
下表显示的是上海市 2001 年 2 月下旬和2002 年同期的每日最高气温,如何对这两段时间的气温进行比较呢?
问题1
2月21日 2月22日 2月23日 2月24日 2月25日 2月26日 2月27日 2月28日
2001年 12 13 14 22 6 8 9 12
2002年 13 13 12 9 11 16 12 10
比较两段时间气温的高低,求平均气温是一种常用的方法
经计算可知这两个时段的平均气温相等,都是12℃,这是不是说,两个时段的气温情况总体上没有什么差异呢?
21日
22日
23日
24日
25日
26日
27日
28日
21日
22日
23日
24日
25日
26日
27日
28日
气温(℃)
气温(℃)
(a)2001年2月下旬
(b)2002年2月下旬
观察下图,你感觉它们有没有差异呢?
通过观察,我们可以发现:图(a)中的点波动范围比较大——从6℃到22℃,图(b)中的点波动范围比较小——从9℃到16℃.
21日
22日
23日
24日
25日
26日
27日
28日
21日
22日
23日
24日
25日
26日
27日
28日
气温(℃)
气温(℃)
(a)2001年2月下旬
(b)2002年2月下旬
观察下图,你感觉它们有没有差异呢?
图(a)中气温的最大值与最小值之间差距很大,相差16℃;图(b)中气温的最大值与最小值相差7℃,总体上气温变化的范围不太大.
问题2
小明和小兵两人参加体育项目训练,近期的 5 次测试成绩如表所示,谁的成绩较为稳定?为什么?
测试次数 1 2 3 4 5
小明 10 14 13 12 13
小兵 11 11 15 14 11
通过计算分析,两人测试成绩的平均数都是12.4,成绩的最大值与最小值也都相差4.
极差=最大值-最小值
16
14
12
10
8
6
4
2
0
1
2
3
4
5
体育项目测试成绩图
从图中我们可以看到:相比之下,小明的成绩大部分集中在平均数附近,而小兵的成绩与其平均数的离散程度略大.
通常,如果一组数与其平均数的离散程度较小,我们就说它比较稳定.
思 考
怎样的指标能反映一组数据与其平均数的离散程度呢?
我们已经看出,小兵的测试成绩与平均数的偏差与小明相比略大.那么如何加以说明呢?可以直接将各数据与平均数的差进行累加吗?
1 2 3 4 5 求和
小明 每次测试成绩 10 14 13 12 13
每次成绩-平均成绩
小兵 每次测试成绩 11 11 15 14 11
每次成绩-平均成绩
在下表中写出你的计算结果.
-2.4
1.6
0.6
-0.4
0.6
0.6
-1.4
-1.4
2.6
1.6
-1.4
0
依据最后求和的结果可以比较两组数据围绕其平均数的波动情况吗?
如果不行,请你提出一个可行的方案,在下表中写上新的计算方案.
思 考
如果一共进行了7次测试,小明因故缺席了2次,怎样比较谁的成绩更稳定?
1 2 3 4 5 6 7 平均
小明 每次测试成绩 10 14 13 缺席 12 缺席 13
小兵 每次测试成绩 11 11 15 14 11 14 11
(每次成绩-平均成绩)2
5.76
2.56
0.36
0.16
0.36
1.84
(每次成绩-平均成绩)2
1.96
1.96
6.76
2.56
1.96
2.56
1.96
2.82
方 差
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况,这个结果称为方差.
我们通常用 s2 表示一组数据的方差,用 表示一组数据的平均数,x1,x2,…,xn表示各个数据,方差的计算公式:
方差主要反映整组数据的波动情况,是反映一组数据与其平均值离散程度的一个重要指标,每个数年据的变化都将影响方差的结果,是一个对整组数据波动情况比较敏感的指标.
在实际使用时,往往计算一组数据的方差,来衡量一组数据的波动大小.
测试次数 1 2 3 4 5
小明 10 14 13 12 13
小兵 11 11 15 14 11
上表中,小明和小兵5次测试成绩的方差的计算式是
计算可得:
小明 5 次测试成绩的方差为_______,
小兵 5 次测试成绩的方差为_______.
计算结果是否是小明的成绩比较稳定呢?
1.84
3.04
归纳总结
方差是用来衡量一组数据的波动大小的特征量
方差越大,数据的波动越大;方差越小,数据的波动越小,通过比较方差的大小来判断数据的稳定性.
随堂演练
1. 计算下列两组数据的平均数和方差:
A 组:0, 10, 5, 5, 5, 5, 5, 5, 5, 5;
B 组:4, 6, 3, 7, 2, 8, 1, 9, 5, 5.
解:A 组的平均数为 5,方差为 5.
B 组的平均数为 5,方差为 6.
2. 甲、乙两台机床生产同种零件,10天出的次品个数分别是:
甲:0,1,0,2,2,0,3,1,2,4
乙:2,3,1,2,0,2,1,1,2,1
分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好?
解:
s2甲>s2乙
∴乙台机床的性能较好
课堂小结
方差是用来衡量一组数据的波动大小的特征量
方差越大,数据的波动越大;方差越小,数据的波动越小,通过比较方差的大小来判断数据的稳定性.
方法小结:
求方差
先平均,再求差,然后平方,最后再平均.
1、已知一组数据-3,x,-2,3,1,6的中位数为1,则其方差为____.
2、小李和小林练习射箭,射完10箭后两人的成绩如图所示,通常新手的成绩不太稳定,根据图中的信息,估计这两人中的新手是 _________.
小李
9
5、某校举行健美操比赛,甲、乙两个班选20名学生参加比赛,两个班参赛学生的平均身高都是1.65米,其方差分别是s甲2=1.9,s乙2=2.4,则参赛学生身高比较整齐的班级是( )
A.甲班 B.乙班
C.同样整齐 D.无法确定
3、要判断小强同学的数学考试成绩是否稳定,那么需要知道他最近几次数学考试成绩的( )
A.方差 B.众数 C.平均数 D.中位数
4、数据0,-1,6,1,x的众数为-1,则这组数据的方差是( )
A
B
A
A
