沪科版八年级数学下册20.2数据的集中趋势与离散程度(第三课时平均数、众数、中位数的综合应用)(共24张PPT)
文档属性
| 名称 | 沪科版八年级数学下册20.2数据的集中趋势与离散程度(第三课时平均数、众数、中位数的综合应用)(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 891.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-23 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
沪科版八年级数学下册
第3课时 平均数、众数、中位数综合应用
20.2 数据的集中趋势与离散程度
一 、数据的集中趋势
进一步认识平均数、中位数、众数都可以
反映一组数据的集中趋势;
1
2
学 习 目 标
了解平均数、中位数、众数各自的特点,能选择适当的量反映数据的集中趋势.
回顾与思考
平均数、中位数、众数分别从哪些方面反映了一组数据的特点?
平均数、中位数和众数都可以反映一组数据的集中趋势
1
3
2
平均数的计算要用到所有的数据,它能够充分利用所有的数据信息,但它受极端值的影响较大
众数是当一组数据中某一数据重复出现较多时,人们往往关心的一个量,众数不受极端值的影响,这是它的一个优势,众数可能不唯一
中位数的计算很少,只与其在数据中的位置有关,但不能充分利用所有的数据信息.也不受极端值的影响.
4
探究与思考
讨论1:
一组数据的平均数、中位数和众数一定在这组数据中吗?
一组数据的平均数和中位数不一定在这组数据里,众数一定在这组数据中.
例如:一组数据从小到大排列后如下:
2、2、3、3、3、4、4、4、5、5
这组数据的平均数为3.5,中位数为3.5,众数为3和4,平均数和中位数均不在数据中,众数在数据中.
一组数据的众数可能不唯一
讨论2:
小明在一次数学检测中得了80分,而全班同学这次检测的平均成绩为75分,因此小明认为他的成绩在全班属中等偏上,你同意他的看法吗?
探究与思考
标准的中等水平是班里所有同学成绩的中位数,而不是平均数.
当成绩排在中间时,成绩属于中等
小明的成绩为 80分,只能说他的成绩高于全班平均分,而其排位不一定在中位数前面,所以不一定属于中上水平.
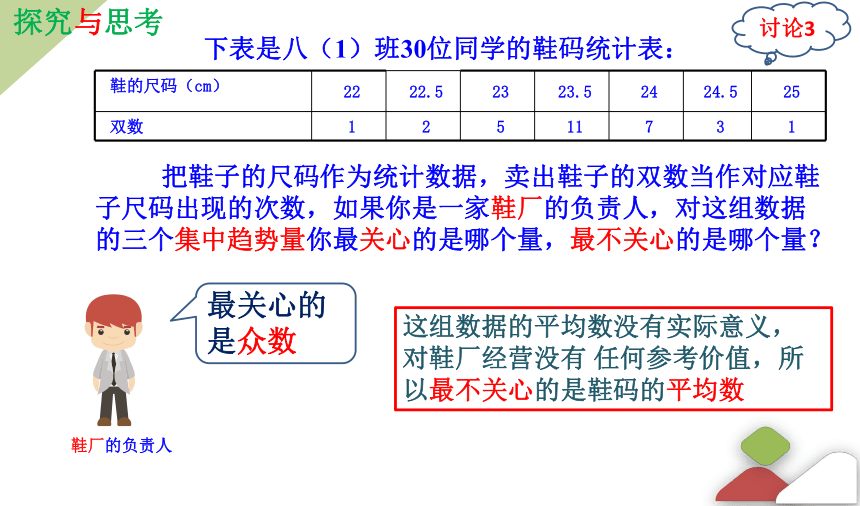
下表是八(1)班30位同学的鞋码统计表:
鞋的尺码(cm) 22 22.5 23 23.5 24 24.5 25
双数 1 2 5 11 7 3 1
把鞋子的尺码作为统计数据,卖出鞋子的双数当作对应鞋子尺码出现的次数,如果你是一家鞋厂的负责人,对这组数据的三个集中趋势量你最关心的是哪个量,最不关心的是哪个量?
最关心的是众数
鞋厂的负责人
这组数据的平均数没有实际意义, 对鞋厂经营没有 任何参考价值,所以最不关心的是鞋码的平均数
探究与思考
讨论3
某家电商场去年7月15日至7月20日,每天销售某种空调数量(单位:台)为:6,8,8,10,12,10. 据此预测,今年下半年销售量可达到1987台,请问是怎样作出预测的?这种预测有道理吗?
这样预测没有道理,因为用来求平均数的样本容量较小,天数过少,没有代表性.同时空调的销售量受天气的影响变化很大.
探究与思考
讨论4
通过样本数据的平均数进行情况估计
(6+8+8+10+12+10)÷5=10.8
10.8×184 ≈1987(台)
用样本的平均数估计总体的平均数,如果样本量太小,往往差异较大
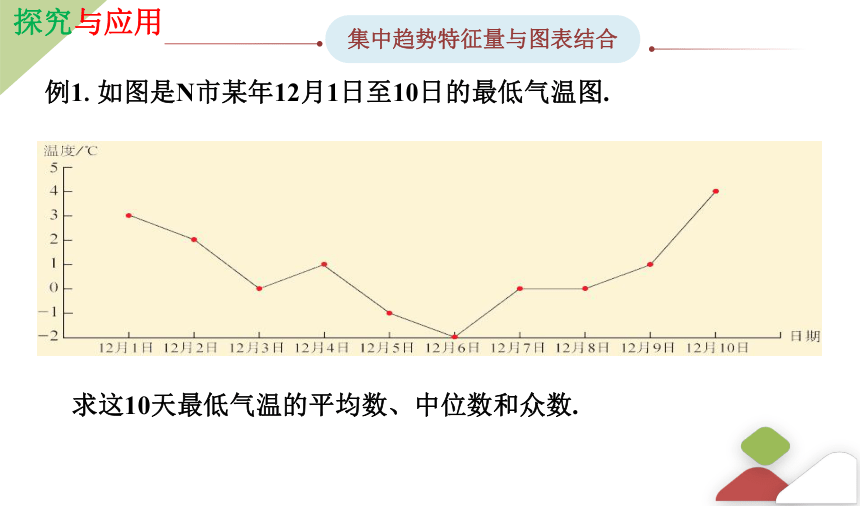
例1.如图是N市某年12月1日至10日的最低气温图.
求这10天最低气温的平均数、中位数和众数.
探究与应用
集中趋势特征量与图表结合
平均数:
中位数:
将这组数据从小到大排列:
-2、-1、0、0、0、1、1、2、3、4
∵(0+1)÷2=0.5
∴中位数:0.5
众数:0
解:由图可得这10天最低气温分别是 :
3℃, 2 ℃, 0 ℃ ,1 ℃ ,-1 ℃ ,-1 ℃, 0 ℃, 0 ℃ ,1 ℃, 4 ℃
例2.某届世界杯足球赛结束后,球迷统计了全部(64场)比赛的进球情况.
求全部比赛进球数的中位数和众数.
进球数 0 1 2 3 4 5 6 7 8
场数 3 15 20 11 8 4 1 1 1
进球数少于2的有18场,多于2的有26场,等于2的有20场,因此可以判断中位数为2,进球数最多的为2球,有20场,所以众数为2.
探究与应用
集中趋势特征量与图表结合
解:
例3、小波学习小组于2022年3月调查了某城市部分居民的家庭人口数,并绘制出下面的扇形统计图.求这部分居民家庭人口数的众数和平均数.
①
②
③
④
⑤
探究与应用
集中趋势特征量与图表结合
≈3.4(人)
由于家庭人口数为3的家庭数在样本中占比最大,所以 这部分居民家庭人口数的众数是3人.
答:这部分居民家庭人口数的众数是3人,平均数为3.4人.
解:
设王波学习小组调查了某城市共n个家庭,则这部分居民家庭人口数的平均数为
①
②
③
④
⑤
例4.6月5日是“世界环境日”,某校“绿色”小组进入明光社区进行一次有关“白色污染”方面的抽样调查,调查结果如下:
如果该社区有500户居民,请你估计该社区居民每天要丢弃多少个废塑料袋?
每户居民平均每天丢弃废塑料袋/个 0 3 4 5 6
户数 2 9 28 16 5
探究与应用
样本平均数估计总体平均水平
解:每户居民每天丢弃废塑料袋的的平均个数为:
500户居民每天丢弃塑料袋个数约为:
4.15×500=2075个.
例5、大理古城是闻名遐迩的历史文化名城,下表是大理古城某历史景点一周抽样统计的参观人数:
此景点的门票价格为:不超过50人时,每人8元;多于50人不超过100人时,每人6元;多于100人时,每人4元.
(1)把上表中一周的参观人数作为一个样本,直接指出这个样本的中位数、众数和平均数.
星期 一 二 三 四 五 六 日
人数 100 120 100 100 160 230 240
探究与应用
集中趋势统计量综合应用
解:
样本的中位数:120
样本的众数:100
样本的平均数:210
此景点的门票价格为:不超过50人时,每人8元;多于50人不超过100人时,每人6元;多于100人时,每人4元.
(2)若“十一”黄金周有甲、乙两个旅行团到该景点参观,两团人数之和恰为上述样本数据的中位数,乙团不超过50人,设两团分别购票共付W元,甲团人数x人. ①求W与x的函数解析式. ②若甲团人数不超过100人,请说明两团合起来购票比分开购票最多可节约多少元?
解:
①、由(1)得样本的中位数:120,
∵乙团不超过50人,∴70≤甲团人数<120
∴W=6x+8(120-x)=960-2x(70≤x<100)
W=4x+8(120-x)=960-4x(100≤x<120)
②
当70≤x<100,两团合起来买票费用比分考购买节约的费用:
Q=960-2x- 120×4=480-2x
∵Q是x的一次函数,且Q随x增大而减小,
∴当x=70是,Q最大值 =340(元)
1、 五个同学的年龄分别是14,15,13,16,14.则中位数 ,众数 .
2、 6名工人某天生产同一零件,生产的件数是:15,17,14,15,17,16这一组数据的中位数是 ,众数 .
14
14
15.5
17、15
实践与练习
填一填
3、已知数据1,3,2,x, 2
(1)如果这组数据的平均数是3,则这组数据的中位数是 ;
(2)如果这组数据的众数是2,则x的值是 .
2
2
1.有一组数据:3,4,5,6,6,则这组数据的平均数、众数、中位数分别是 ( )
A. 4.8,6,6 B. 5,5,5
C. 4.8,6,5 D. 5,6,6
2.某篮球队12名队员的年龄如表所示:
则这12名队员年龄的众数和中位数分别是 ( )
A. 2,19 B. 18,19
C. 2,19.5 D. 18,19.5
C
B
实践与练习
选一选
3、为了让人们感受随地丢弃废电池对环境造成的影响,某班环保小组的6名同学记录了一学期内自己家中用完的电池数量,结果如下(单位:节):33,25,28,26,25,31.如果该班有45名学生,那么根据所提供的数据,请你估计一下,一学期内全班同学总共用完的电池数量约为 ( )
A.7 560节 B. 1 260节
C. 1 080节 D. 900节
B
4、小王参加招聘测试,他的笔试、面试、技能操作得分分别为85分、80分、90分,若依次按照2 ∶3 ∶5的比例确定成绩,则小王的成绩是( )
A. 255分 B. 84分 C. 84.5分 D. 86分
D
5、在2020年抗击“新冠”时期的“线上课堂”学习活动中,李老师从3月8日至3月14日在网上答题个数的记录如下表:
日期
5月8日
5月9日
5月10日
5月11日
5月12日
5月13日
5月14日
答题个数
68
55
50
56
54
48
68
在李老师每天的答题个数所组成的这组数据中,众数和中位数依次是( )
A. 68,55 B. 55,68 C. 68,57 D. 55,57
A
68 68 56 55 54 50 48
1、.已知一组数据10,10,x,8(由大到小排列)的中位数与平均数相等,求x值及这组数据的中位数.
解:∵10,10,x,8的中位数与平均数相等
∴ (10+x)/2=(10+10+x+8)/4
∴x=8
(10+x)/2=9
∴这组数据中的中位数是9.
实践与练习
算一算
2.老王家的鱼塘中放养了某种鱼1500条,若干年后,准备打捞出售,为了估计鱼塘中这种鱼的总质量,现从鱼塘中捕捞三次,得到数据如下表:
(1)鱼塘中这种鱼平均每条重多少千克?
(2)若这种鱼放养的成活率是80%,鱼塘中这种鱼约有多少千克?
解:
(1)样本平均数:
(2)1500×80%×2.84=3408(千克)
1、 质量检测部门对甲、乙、丙三家公司销售产品的使用寿命进行了跟踪调查,统计结果如下(单位:年):
甲公司:4,5,5,5,5,7,9,12,13,15;
乙公司:6,6,8,8,8,9,10,12,14,15;
丙公司:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
综合与提升
(1)甲、乙、丙三家公司在该产品的销售中都声称,其销售的该产品的使用寿命是8年,你如何理解他们的宣传;(请用已学的统计量中加以说明)
(2)如果你是顾客,你将选购哪家公司销售的产品,为什么?
(3)如果你是丙公司的推销员,你将如何结合上述数据,对本公司的产品进行推销?
解:(1)甲厂:平均数为 (4+5+5+5+5+7+9+12+13+15)=8,
众数为5,中位数为6;
乙厂:平均数为 (6+6+8+8+8+9+10+12+14+15)=9.6,
众数为8,中位数为8.5;
丙厂:平均数为 (4+4+4+6+7+9+13+15+16+16)=9.4,
众数为4,中位数为8;
∴甲公司用的是平均数;乙公司用的是众数;丙公司用的是中位数.
(2)乙公司.因为从平均数、众数和中位数三项指标上看,都比其他的两个公司要好,他们的产品质量更高.
(3)①丙公司的平均数和中位数都比甲公司高;②以从产品寿命的最高年限考虑购买丙公司的产品的使用寿命比较高的机会比乙公司产品大一些.
沪科版八年级数学下册
第3课时 平均数、众数、中位数综合应用
20.2 数据的集中趋势与离散程度
一 、数据的集中趋势
进一步认识平均数、中位数、众数都可以
反映一组数据的集中趋势;
1
2
学 习 目 标
了解平均数、中位数、众数各自的特点,能选择适当的量反映数据的集中趋势.
回顾与思考
平均数、中位数、众数分别从哪些方面反映了一组数据的特点?
平均数、中位数和众数都可以反映一组数据的集中趋势
1
3
2
平均数的计算要用到所有的数据,它能够充分利用所有的数据信息,但它受极端值的影响较大
众数是当一组数据中某一数据重复出现较多时,人们往往关心的一个量,众数不受极端值的影响,这是它的一个优势,众数可能不唯一
中位数的计算很少,只与其在数据中的位置有关,但不能充分利用所有的数据信息.也不受极端值的影响.
4
探究与思考
讨论1:
一组数据的平均数、中位数和众数一定在这组数据中吗?
一组数据的平均数和中位数不一定在这组数据里,众数一定在这组数据中.
例如:一组数据从小到大排列后如下:
2、2、3、3、3、4、4、4、5、5
这组数据的平均数为3.5,中位数为3.5,众数为3和4,平均数和中位数均不在数据中,众数在数据中.
一组数据的众数可能不唯一
讨论2:
小明在一次数学检测中得了80分,而全班同学这次检测的平均成绩为75分,因此小明认为他的成绩在全班属中等偏上,你同意他的看法吗?
探究与思考
标准的中等水平是班里所有同学成绩的中位数,而不是平均数.
当成绩排在中间时,成绩属于中等
小明的成绩为 80分,只能说他的成绩高于全班平均分,而其排位不一定在中位数前面,所以不一定属于中上水平.
下表是八(1)班30位同学的鞋码统计表:
鞋的尺码(cm) 22 22.5 23 23.5 24 24.5 25
双数 1 2 5 11 7 3 1
把鞋子的尺码作为统计数据,卖出鞋子的双数当作对应鞋子尺码出现的次数,如果你是一家鞋厂的负责人,对这组数据的三个集中趋势量你最关心的是哪个量,最不关心的是哪个量?
最关心的是众数
鞋厂的负责人
这组数据的平均数没有实际意义, 对鞋厂经营没有 任何参考价值,所以最不关心的是鞋码的平均数
探究与思考
讨论3
某家电商场去年7月15日至7月20日,每天销售某种空调数量(单位:台)为:6,8,8,10,12,10. 据此预测,今年下半年销售量可达到1987台,请问是怎样作出预测的?这种预测有道理吗?
这样预测没有道理,因为用来求平均数的样本容量较小,天数过少,没有代表性.同时空调的销售量受天气的影响变化很大.
探究与思考
讨论4
通过样本数据的平均数进行情况估计
(6+8+8+10+12+10)÷5=10.8
10.8×184 ≈1987(台)
用样本的平均数估计总体的平均数,如果样本量太小,往往差异较大
例1.如图是N市某年12月1日至10日的最低气温图.
求这10天最低气温的平均数、中位数和众数.
探究与应用
集中趋势特征量与图表结合
平均数:
中位数:
将这组数据从小到大排列:
-2、-1、0、0、0、1、1、2、3、4
∵(0+1)÷2=0.5
∴中位数:0.5
众数:0
解:由图可得这10天最低气温分别是 :
3℃, 2 ℃, 0 ℃ ,1 ℃ ,-1 ℃ ,-1 ℃, 0 ℃, 0 ℃ ,1 ℃, 4 ℃
例2.某届世界杯足球赛结束后,球迷统计了全部(64场)比赛的进球情况.
求全部比赛进球数的中位数和众数.
进球数 0 1 2 3 4 5 6 7 8
场数 3 15 20 11 8 4 1 1 1
进球数少于2的有18场,多于2的有26场,等于2的有20场,因此可以判断中位数为2,进球数最多的为2球,有20场,所以众数为2.
探究与应用
集中趋势特征量与图表结合
解:
例3、小波学习小组于2022年3月调查了某城市部分居民的家庭人口数,并绘制出下面的扇形统计图.求这部分居民家庭人口数的众数和平均数.
①
②
③
④
⑤
探究与应用
集中趋势特征量与图表结合
≈3.4(人)
由于家庭人口数为3的家庭数在样本中占比最大,所以 这部分居民家庭人口数的众数是3人.
答:这部分居民家庭人口数的众数是3人,平均数为3.4人.
解:
设王波学习小组调查了某城市共n个家庭,则这部分居民家庭人口数的平均数为
①
②
③
④
⑤
例4.6月5日是“世界环境日”,某校“绿色”小组进入明光社区进行一次有关“白色污染”方面的抽样调查,调查结果如下:
如果该社区有500户居民,请你估计该社区居民每天要丢弃多少个废塑料袋?
每户居民平均每天丢弃废塑料袋/个 0 3 4 5 6
户数 2 9 28 16 5
探究与应用
样本平均数估计总体平均水平
解:每户居民每天丢弃废塑料袋的的平均个数为:
500户居民每天丢弃塑料袋个数约为:
4.15×500=2075个.
例5、大理古城是闻名遐迩的历史文化名城,下表是大理古城某历史景点一周抽样统计的参观人数:
此景点的门票价格为:不超过50人时,每人8元;多于50人不超过100人时,每人6元;多于100人时,每人4元.
(1)把上表中一周的参观人数作为一个样本,直接指出这个样本的中位数、众数和平均数.
星期 一 二 三 四 五 六 日
人数 100 120 100 100 160 230 240
探究与应用
集中趋势统计量综合应用
解:
样本的中位数:120
样本的众数:100
样本的平均数:210
此景点的门票价格为:不超过50人时,每人8元;多于50人不超过100人时,每人6元;多于100人时,每人4元.
(2)若“十一”黄金周有甲、乙两个旅行团到该景点参观,两团人数之和恰为上述样本数据的中位数,乙团不超过50人,设两团分别购票共付W元,甲团人数x人. ①求W与x的函数解析式. ②若甲团人数不超过100人,请说明两团合起来购票比分开购票最多可节约多少元?
解:
①、由(1)得样本的中位数:120,
∵乙团不超过50人,∴70≤甲团人数<120
∴W=6x+8(120-x)=960-2x(70≤x<100)
W=4x+8(120-x)=960-4x(100≤x<120)
②
当70≤x<100,两团合起来买票费用比分考购买节约的费用:
Q=960-2x- 120×4=480-2x
∵Q是x的一次函数,且Q随x增大而减小,
∴当x=70是,Q最大值 =340(元)
1、 五个同学的年龄分别是14,15,13,16,14.则中位数 ,众数 .
2、 6名工人某天生产同一零件,生产的件数是:15,17,14,15,17,16这一组数据的中位数是 ,众数 .
14
14
15.5
17、15
实践与练习
填一填
3、已知数据1,3,2,x, 2
(1)如果这组数据的平均数是3,则这组数据的中位数是 ;
(2)如果这组数据的众数是2,则x的值是 .
2
2
1.有一组数据:3,4,5,6,6,则这组数据的平均数、众数、中位数分别是 ( )
A. 4.8,6,6 B. 5,5,5
C. 4.8,6,5 D. 5,6,6
2.某篮球队12名队员的年龄如表所示:
则这12名队员年龄的众数和中位数分别是 ( )
A. 2,19 B. 18,19
C. 2,19.5 D. 18,19.5
C
B
实践与练习
选一选
3、为了让人们感受随地丢弃废电池对环境造成的影响,某班环保小组的6名同学记录了一学期内自己家中用完的电池数量,结果如下(单位:节):33,25,28,26,25,31.如果该班有45名学生,那么根据所提供的数据,请你估计一下,一学期内全班同学总共用完的电池数量约为 ( )
A.7 560节 B. 1 260节
C. 1 080节 D. 900节
B
4、小王参加招聘测试,他的笔试、面试、技能操作得分分别为85分、80分、90分,若依次按照2 ∶3 ∶5的比例确定成绩,则小王的成绩是( )
A. 255分 B. 84分 C. 84.5分 D. 86分
D
5、在2020年抗击“新冠”时期的“线上课堂”学习活动中,李老师从3月8日至3月14日在网上答题个数的记录如下表:
日期
5月8日
5月9日
5月10日
5月11日
5月12日
5月13日
5月14日
答题个数
68
55
50
56
54
48
68
在李老师每天的答题个数所组成的这组数据中,众数和中位数依次是( )
A. 68,55 B. 55,68 C. 68,57 D. 55,57
A
68 68 56 55 54 50 48
1、.已知一组数据10,10,x,8(由大到小排列)的中位数与平均数相等,求x值及这组数据的中位数.
解:∵10,10,x,8的中位数与平均数相等
∴ (10+x)/2=(10+10+x+8)/4
∴x=8
(10+x)/2=9
∴这组数据中的中位数是9.
实践与练习
算一算
2.老王家的鱼塘中放养了某种鱼1500条,若干年后,准备打捞出售,为了估计鱼塘中这种鱼的总质量,现从鱼塘中捕捞三次,得到数据如下表:
(1)鱼塘中这种鱼平均每条重多少千克?
(2)若这种鱼放养的成活率是80%,鱼塘中这种鱼约有多少千克?
解:
(1)样本平均数:
(2)1500×80%×2.84=3408(千克)
1、 质量检测部门对甲、乙、丙三家公司销售产品的使用寿命进行了跟踪调查,统计结果如下(单位:年):
甲公司:4,5,5,5,5,7,9,12,13,15;
乙公司:6,6,8,8,8,9,10,12,14,15;
丙公司:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
综合与提升
(1)甲、乙、丙三家公司在该产品的销售中都声称,其销售的该产品的使用寿命是8年,你如何理解他们的宣传;(请用已学的统计量中加以说明)
(2)如果你是顾客,你将选购哪家公司销售的产品,为什么?
(3)如果你是丙公司的推销员,你将如何结合上述数据,对本公司的产品进行推销?
解:(1)甲厂:平均数为 (4+5+5+5+5+7+9+12+13+15)=8,
众数为5,中位数为6;
乙厂:平均数为 (6+6+8+8+8+9+10+12+14+15)=9.6,
众数为8,中位数为8.5;
丙厂:平均数为 (4+4+4+6+7+9+13+15+16+16)=9.4,
众数为4,中位数为8;
∴甲公司用的是平均数;乙公司用的是众数;丙公司用的是中位数.
(2)乙公司.因为从平均数、众数和中位数三项指标上看,都比其他的两个公司要好,他们的产品质量更高.
(3)①丙公司的平均数和中位数都比甲公司高;②以从产品寿命的最高年限考虑购买丙公司的产品的使用寿命比较高的机会比乙公司产品大一些.
