北师大版七年级下册 2.3 平行线的性质课件(共16张PPT)
文档属性
| 名称 | 北师大版七年级下册 2.3 平行线的性质课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 361.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-23 19:07:28 | ||
图片预览




文档简介
(共17张PPT)
3 平行线的性质
北师大版 七年级下册
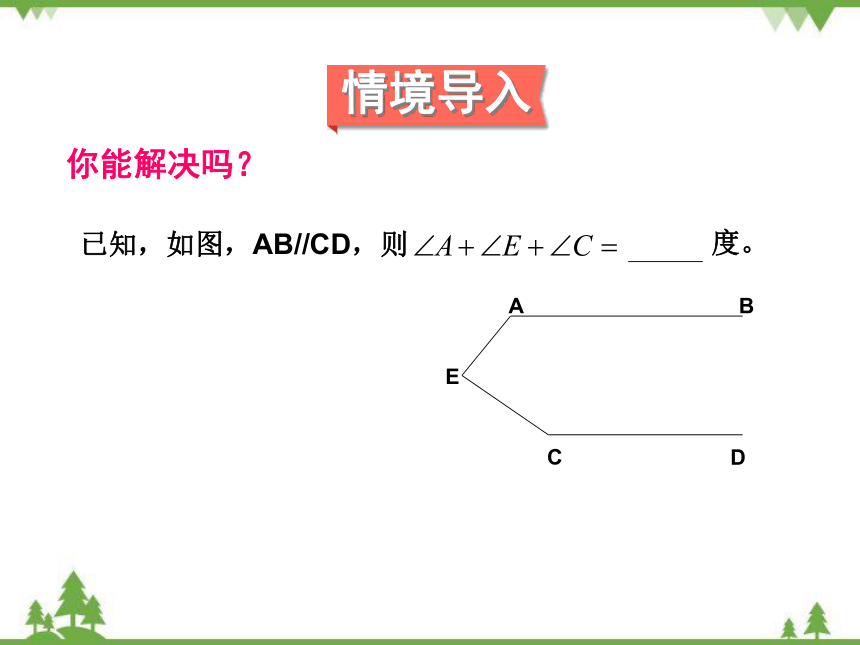
你能解决吗?
已知,如图,AB//CD,则
度。
A
B
C
D
E
情境导入
1.什么叫平行线?
2.指出下图中各对角是哪两条直线被哪一条直线所载
而得到的什么角?
E
A
B
C
D
1
2
3
3.已知,如图,
试说明:
①.
②.
AB//CD
AD//BC
A
B
C
D
解:① ∵
∴
AB//CD
(已知)
(同旁内角互补,两直线平行)
② ∵
∴
(已知)
(等量代换)
∴
AD//BC
(同旁内角互补,两直线平行)
知识回顾
1.用前面学过的画平行线的方法
画两条平行线: a∥b
2.用第三条直线 l 去截这两条平行线,找找其中的同位角、内错角和同旁内角,猜一猜它们的数量关系,并用量角器去测量验证。
3.归纳你得到的结论:
(1)两直线平行,同位角相等
(2)两直线平行,内错角相等,
(3)两直线平行,同旁内角互补,
∵ a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
探索新知
4.概括平行线的性质:
(1). 两直线平行,同位角相等。
(2). 两直线平行,内错角相等。
(3). 两直线平行,同旁内角互补。
5.理解,记忆
(1).区别异同。
(2).与平行线的判定区别。
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行。
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补。
平行线的判定
平行线的性质
对
比
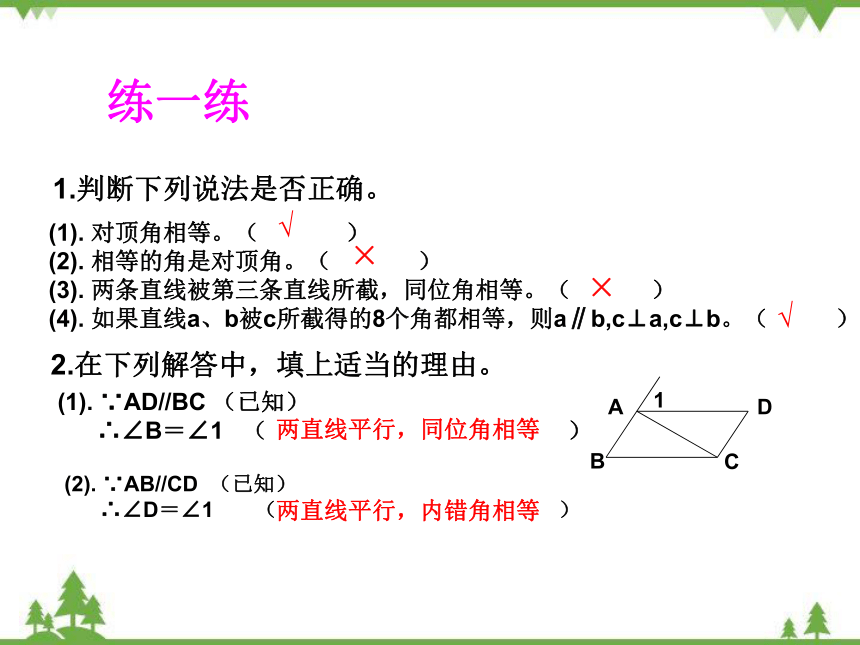
1.判断下列说法是否正确。
(1). 对顶角相等。( )
(2). 相等的角是对顶角。( )
(3). 两条直线被第三条直线所截,同位角相等。( )
(4). 如果直线a、b被c所截得的8个角都相等,则a∥b,c⊥a,c⊥b。( )
√
×
×
√
2.在下列解答中,填上适当的理由。
(1). ∵AD//BC (已知)
∴∠B=∠1 ( )
1
A
B
C
D
(2). ∵AB//CD (已知)
∴∠D=∠1 ( )
两直线平行,同位角相等
两直线平行,内错角相等
练一练
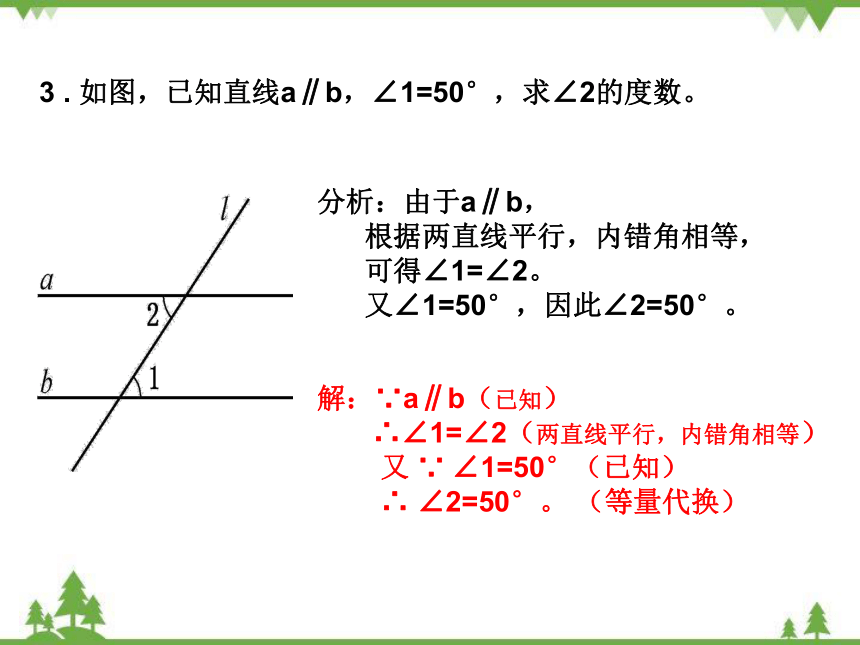
3 . 如图,已知直线a∥b,∠1=50°,求∠2的度数。
分析:由于a∥b,
根据两直线平行,内错角相等,
可得∠1=∠2。
又∠1=50°,因此∠2=50°。
解:∵a∥b(已知)
∴∠1=∠2(两直线平行,内错角相等)
又 ∵ ∠1=50°(已知)
∴ ∠2=50°。 (等量代换)
1. 如图,在四边形ABCD中,已知AB∥CD,∠B=60°,求∠C的度数。能否求得∠A的度数 ?
分析:由于AB∥CD ,
根据两直线平行,同旁内角互补 ,
可得∠B+∠C=180° 。
又∠B=60° ,因此∠C=120° 。
根据题目的已知条件,无法求出
∠A的度数。
解:∵ AB∥CD (已知)
∴ ∠B+∠C=180° (两直线平行,同旁内角互补 )
又 ∵ ∠B=60° (已知)
∴ ∠C=120° 。 (等式的性质)
根据题目的已知条件,无法求出∠A的度数。
随堂演练
2. 如图,
(1)如果AD∥BC,那么根据两直线平行,同旁内角互补,可得∠_______+∠ABC =180°;
(2)如果AB∥CD,那么根据两直线平行,同旁内角互补,可得∠_______+∠ABC =180°。
(1) ∵ AD∥BC (已知)
∴∠DAB+∠ABC=180°(两直线平行,
同旁内角互补)
(2) ∵ AB∥CD (已知)
∴∠DCB+∠ABC=180°(两直线平行,
同旁内角互补)
DAB
DCB
3. 在图上画着与第三条直线相交的两条平行线,如果∠1=52° ,那么∠2= , ∠3= , ∠4= .
52°
128°
52°
1. 如图,已知直线a∥b,
∠3=131°,求∠ 1、∠2的度数。
解(1)∵∠1=∠3 (对顶角相等)
且∠3=131°(已知)
∴∠1 =131° (等量代换)
(2)∵a∥b(已知)
∴∠1+∠2=180°(两直线平行,
同旁内角互补)
又 ∵ ∠1=131° (已知)
∴ ∠2=49°。 (等式性质)
巩固提升
2. 已知,如图,AC//FD,
试说明:EC//BD
A
B
C
D
E
F
1
2
解:∵ AC//FD ( )
∴ ∠A=∠2 ( )
∵ ∠1=∠A,∠B=∠2 ( )
∴ ∠1=∠B ( )
已知
两直线平行,同位角相等
已知
等量代换
∴ EC//BD ( )
同位角相等,两直线平行
你能解决吗?
已知,如图,AB//CD,则
度。
A
B
C
D
E
A
B
C
D
E
F
解法一:
连结AC
∵ AB//CD ( )
已知
∴ ∠BAC+∠ACD=180
( )
0
两直线平行,同旁内角互补
三角形内角和
∵ ∠E+∠EAC+∠ACE=180 ( )
0
∴ ∠BAE+∠E+∠ACE=360 ( )
0
等式性质
解法二:
过点E作EF//AB
360
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
青年人首先要树雄心,立大志;其次要度衡量力,决心为国家人民作一个有用的人才;为此就要选择一个奋斗的目标来努力学习和实践。
—— 吴玉章
3 平行线的性质
北师大版 七年级下册
你能解决吗?
已知,如图,AB//CD,则
度。
A
B
C
D
E
情境导入
1.什么叫平行线?
2.指出下图中各对角是哪两条直线被哪一条直线所载
而得到的什么角?
E
A
B
C
D
1
2
3
3.已知,如图,
试说明:
①.
②.
AB//CD
AD//BC
A
B
C
D
解:① ∵
∴
AB//CD
(已知)
(同旁内角互补,两直线平行)
② ∵
∴
(已知)
(等量代换)
∴
AD//BC
(同旁内角互补,两直线平行)
知识回顾
1.用前面学过的画平行线的方法
画两条平行线: a∥b
2.用第三条直线 l 去截这两条平行线,找找其中的同位角、内错角和同旁内角,猜一猜它们的数量关系,并用量角器去测量验证。
3.归纳你得到的结论:
(1)两直线平行,同位角相等
(2)两直线平行,内错角相等,
(3)两直线平行,同旁内角互补,
∵ a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
探索新知
4.概括平行线的性质:
(1). 两直线平行,同位角相等。
(2). 两直线平行,内错角相等。
(3). 两直线平行,同旁内角互补。
5.理解,记忆
(1).区别异同。
(2).与平行线的判定区别。
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行。
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补。
平行线的判定
平行线的性质
对
比
1.判断下列说法是否正确。
(1). 对顶角相等。( )
(2). 相等的角是对顶角。( )
(3). 两条直线被第三条直线所截,同位角相等。( )
(4). 如果直线a、b被c所截得的8个角都相等,则a∥b,c⊥a,c⊥b。( )
√
×
×
√
2.在下列解答中,填上适当的理由。
(1). ∵AD//BC (已知)
∴∠B=∠1 ( )
1
A
B
C
D
(2). ∵AB//CD (已知)
∴∠D=∠1 ( )
两直线平行,同位角相等
两直线平行,内错角相等
练一练
3 . 如图,已知直线a∥b,∠1=50°,求∠2的度数。
分析:由于a∥b,
根据两直线平行,内错角相等,
可得∠1=∠2。
又∠1=50°,因此∠2=50°。
解:∵a∥b(已知)
∴∠1=∠2(两直线平行,内错角相等)
又 ∵ ∠1=50°(已知)
∴ ∠2=50°。 (等量代换)
1. 如图,在四边形ABCD中,已知AB∥CD,∠B=60°,求∠C的度数。能否求得∠A的度数 ?
分析:由于AB∥CD ,
根据两直线平行,同旁内角互补 ,
可得∠B+∠C=180° 。
又∠B=60° ,因此∠C=120° 。
根据题目的已知条件,无法求出
∠A的度数。
解:∵ AB∥CD (已知)
∴ ∠B+∠C=180° (两直线平行,同旁内角互补 )
又 ∵ ∠B=60° (已知)
∴ ∠C=120° 。 (等式的性质)
根据题目的已知条件,无法求出∠A的度数。
随堂演练
2. 如图,
(1)如果AD∥BC,那么根据两直线平行,同旁内角互补,可得∠_______+∠ABC =180°;
(2)如果AB∥CD,那么根据两直线平行,同旁内角互补,可得∠_______+∠ABC =180°。
(1) ∵ AD∥BC (已知)
∴∠DAB+∠ABC=180°(两直线平行,
同旁内角互补)
(2) ∵ AB∥CD (已知)
∴∠DCB+∠ABC=180°(两直线平行,
同旁内角互补)
DAB
DCB
3. 在图上画着与第三条直线相交的两条平行线,如果∠1=52° ,那么∠2= , ∠3= , ∠4= .
52°
128°
52°
1. 如图,已知直线a∥b,
∠3=131°,求∠ 1、∠2的度数。
解(1)∵∠1=∠3 (对顶角相等)
且∠3=131°(已知)
∴∠1 =131° (等量代换)
(2)∵a∥b(已知)
∴∠1+∠2=180°(两直线平行,
同旁内角互补)
又 ∵ ∠1=131° (已知)
∴ ∠2=49°。 (等式性质)
巩固提升
2. 已知,如图,AC//FD,
试说明:EC//BD
A
B
C
D
E
F
1
2
解:∵ AC//FD ( )
∴ ∠A=∠2 ( )
∵ ∠1=∠A,∠B=∠2 ( )
∴ ∠1=∠B ( )
已知
两直线平行,同位角相等
已知
等量代换
∴ EC//BD ( )
同位角相等,两直线平行
你能解决吗?
已知,如图,AB//CD,则
度。
A
B
C
D
E
A
B
C
D
E
F
解法一:
连结AC
∵ AB//CD ( )
已知
∴ ∠BAC+∠ACD=180
( )
0
两直线平行,同旁内角互补
三角形内角和
∵ ∠E+∠EAC+∠ACE=180 ( )
0
∴ ∠BAE+∠E+∠ACE=360 ( )
0
等式性质
解法二:
过点E作EF//AB
360
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
青年人首先要树雄心,立大志;其次要度衡量力,决心为国家人民作一个有用的人才;为此就要选择一个奋斗的目标来努力学习和实践。
—— 吴玉章
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
