北师大版七年级下册 2.4 用尺规作角课件(共18张PPT)
文档属性
| 名称 | 北师大版七年级下册 2.4 用尺规作角课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 943.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-23 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
第二章 相交线与平行线
4 用尺规作角
学习目标
1.能用尺规作一个角等于已知角.
2.能利用尺规作角的和、差、倍.
尺规作图的基本步骤是什么?
提示:(1)写出已知.(2)写出求作.(3)写出作法并作图.注意:作图时要保留_________.有时,根据题目要求,可省略作法.
作图痕迹
温故知新
利用没有刻度的直尺和圆规的几何作图称为尺规作图。
尺规作图的概念是什么?
如何用圆规和直尺作一条线段等于已知线段?
已知:线段AB.
求作:线段A’ B’,使A’ B’=AB.
A
B
作法与示范:
(1) 作射线A’C’ ;
A’ C’
(2) 以点A’为圆心,
以AB的长为半径
画弧,
交射线A’ C’于点B’,
B’
A’
A’B’ 就是所求作的线段。
示 范
作 法
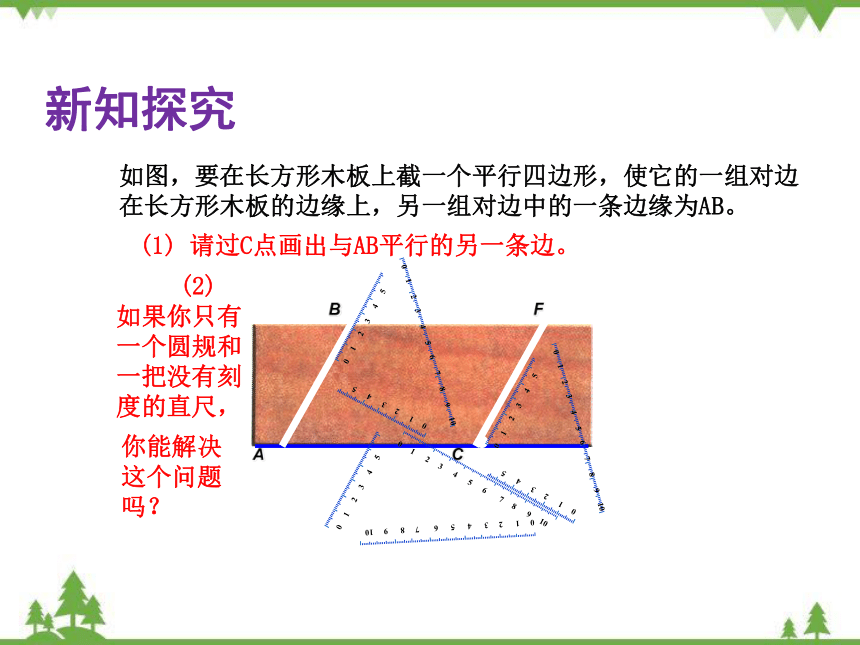
如图,要在长方形木板上截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边缘为AB。
A
B
(1) 请过C点画出与AB平行的另一条边。
C
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
F
(2) 如果你只有一个圆规和一把没有刻度的直尺,
你能解决这个问题吗?
新知探究
A
B
F
C
上述问题:
用尺规(无刻度的直尺和圆规)
“过直线外一点作已知直线的平行线”
相当于
“过点C作∠ECF
E
等于已知角∠CAB.”
已知: ∠AOB。
作一个角等于已知角
求作: ∠A’O’B’ 使∠A’O’B’=∠AOB。
B
O
A
O’
A’
(2) 以点O为圆心,
任意长为半径
交OA于点C,
(3) 以点O’为圆心,
画弧,
C
D
同样(OC)长为半径
画弧,
C’
(4) 以点C’为圆心,
CD长为半径
画弧,
D’
(5) 过点D’作射线O’B’.
B’
A’
O’
B’
∠A’O’B’就是所求的角.
作 法 示 范
(1) 作射线O’A’;
交OB于点D;
交O’A’于点C’;
交前面的弧于点D’ ,
解决前面的问题如下:
A
B
C
分析:若以点C为顶点作一个与∠BAC既同位又相等的角∠FCE, 则∠FCE的边CF所在的直线即为所求.
E
G
G’
H
D
F
例1 已知: ∠AOB.
利用尺规作: ∠A’O’B’
使∠A’O’B’=2∠AOB.
B
O(O’)
A
作法一:
C
A’
B’
∠A’O’B’为所求.
B
O
A
作法二:
C
D
C’
E
B’
O’
A
∠A’O’B’为所求.
新知巩固
例2 过直线外一点P作已知直线l的平行线.
解:已知:直线l及l外一点P,
求作:直线l′,使l′过P点且l′∥l.
作法:1.过点P任意作直线a与l
交于Q.
2.以P为顶点,直线a为角的一边,
在直线a同旁作∠2,使∠2=∠1
(如图),则∠2的另一边所在直线l′即为所求.
1.尺规作图就是( )
(A)用直尺按一定的规矩作图
(B)用直尺和圆规作图
(C)用三角尺和圆规作图
(D)用没有刻度的直尺和圆规作图
解析:根据尺规作图的概念可知选D.
答案:D
课堂练习
2.下列尺规作图的语句错误的是( )
(A)作∠AOB,使∠AOB=3∠α
(B)以点O为圆心作弧
(C)以点A为圆心,线段a的长为半径作弧
(D)作∠ABC,使∠ABC=∠α+∠β
解析:作弧必须有圆心和半径,缺一不可,故B选项错误.
答案:选B.
3.如图,已知∠A,∠B,求作一个角,使它等于∠A-∠B.(不用写作法,保留作图痕迹)
解:作∠COD=∠A,并在∠COD的内部作∠DOE=∠B,则∠COE就是所求作的角.
作一个角等于已知角可以归纳为“一线三弧”
先画一条射线,再作三次弧.其中前两次弧半径相同,而第三次以原角的两边与弧的交点之间的距离为半径.
课堂小结
第二章 相交线与平行线
4 用尺规作角
学习目标
1.能用尺规作一个角等于已知角.
2.能利用尺规作角的和、差、倍.
尺规作图的基本步骤是什么?
提示:(1)写出已知.(2)写出求作.(3)写出作法并作图.注意:作图时要保留_________.有时,根据题目要求,可省略作法.
作图痕迹
温故知新
利用没有刻度的直尺和圆规的几何作图称为尺规作图。
尺规作图的概念是什么?
如何用圆规和直尺作一条线段等于已知线段?
已知:线段AB.
求作:线段A’ B’,使A’ B’=AB.
A
B
作法与示范:
(1) 作射线A’C’ ;
A’ C’
(2) 以点A’为圆心,
以AB的长为半径
画弧,
交射线A’ C’于点B’,
B’
A’
A’B’ 就是所求作的线段。
示 范
作 法
如图,要在长方形木板上截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边缘为AB。
A
B
(1) 请过C点画出与AB平行的另一条边。
C
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
F
(2) 如果你只有一个圆规和一把没有刻度的直尺,
你能解决这个问题吗?
新知探究
A
B
F
C
上述问题:
用尺规(无刻度的直尺和圆规)
“过直线外一点作已知直线的平行线”
相当于
“过点C作∠ECF
E
等于已知角∠CAB.”
已知: ∠AOB。
作一个角等于已知角
求作: ∠A’O’B’ 使∠A’O’B’=∠AOB。
B
O
A
O’
A’
(2) 以点O为圆心,
任意长为半径
交OA于点C,
(3) 以点O’为圆心,
画弧,
C
D
同样(OC)长为半径
画弧,
C’
(4) 以点C’为圆心,
CD长为半径
画弧,
D’
(5) 过点D’作射线O’B’.
B’
A’
O’
B’
∠A’O’B’就是所求的角.
作 法 示 范
(1) 作射线O’A’;
交OB于点D;
交O’A’于点C’;
交前面的弧于点D’ ,
解决前面的问题如下:
A
B
C
分析:若以点C为顶点作一个与∠BAC既同位又相等的角∠FCE, 则∠FCE的边CF所在的直线即为所求.
E
G
G’
H
D
F
例1 已知: ∠AOB.
利用尺规作: ∠A’O’B’
使∠A’O’B’=2∠AOB.
B
O(O’)
A
作法一:
C
A’
B’
∠A’O’B’为所求.
B
O
A
作法二:
C
D
C’
E
B’
O’
A
∠A’O’B’为所求.
新知巩固
例2 过直线外一点P作已知直线l的平行线.
解:已知:直线l及l外一点P,
求作:直线l′,使l′过P点且l′∥l.
作法:1.过点P任意作直线a与l
交于Q.
2.以P为顶点,直线a为角的一边,
在直线a同旁作∠2,使∠2=∠1
(如图),则∠2的另一边所在直线l′即为所求.
1.尺规作图就是( )
(A)用直尺按一定的规矩作图
(B)用直尺和圆规作图
(C)用三角尺和圆规作图
(D)用没有刻度的直尺和圆规作图
解析:根据尺规作图的概念可知选D.
答案:D
课堂练习
2.下列尺规作图的语句错误的是( )
(A)作∠AOB,使∠AOB=3∠α
(B)以点O为圆心作弧
(C)以点A为圆心,线段a的长为半径作弧
(D)作∠ABC,使∠ABC=∠α+∠β
解析:作弧必须有圆心和半径,缺一不可,故B选项错误.
答案:选B.
3.如图,已知∠A,∠B,求作一个角,使它等于∠A-∠B.(不用写作法,保留作图痕迹)
解:作∠COD=∠A,并在∠COD的内部作∠DOE=∠B,则∠COE就是所求作的角.
作一个角等于已知角可以归纳为“一线三弧”
先画一条射线,再作三次弧.其中前两次弧半径相同,而第三次以原角的两边与弧的交点之间的距离为半径.
课堂小结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
