人教版数学六年级下册 3.7 解决问题 课件(19张PPT)
文档属性
| 名称 | 人教版数学六年级下册 3.7 解决问题 课件(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-23 10:23:14 | ||
图片预览




文档简介
(共20张PPT)
解 决 问 题
学习目标
1.通过把不规则形状的体积转化成规则形状,把未知知识转化为已学知识,发现转化过程中的“变”与“不变”,提高学生分析问题和解决问题的能力。
2.渗透等积变形的思想,提高学生的学习兴趣。
学习重点
学习难点
求不规则物体的体积。
用转化法解决不规则物体的容积问题。
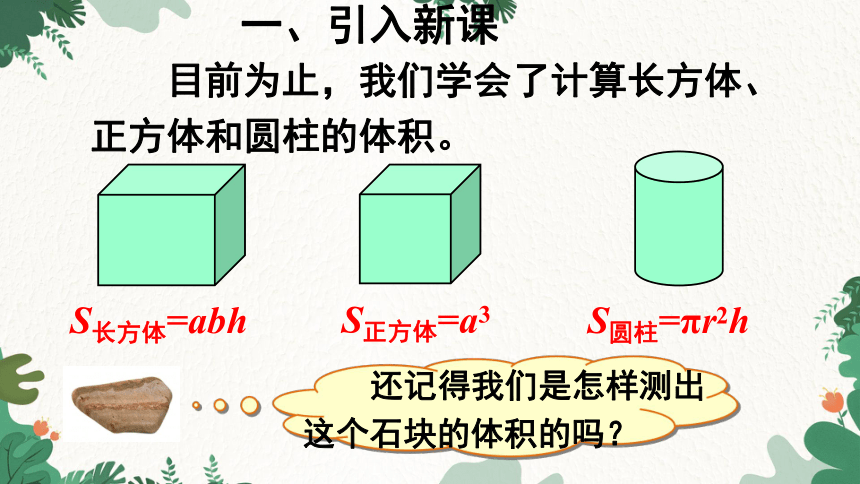
一、引入新课
目前为止,我们学会了计算长方体、正方体和圆柱的体积。
S长方体=abh
S正方体=a3
S圆柱=πr2h
还记得我们是怎样测出这个石块的体积的吗?
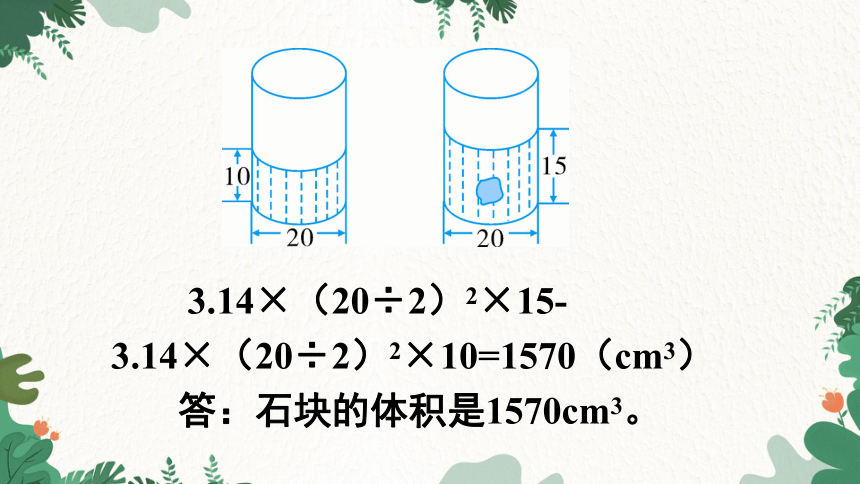
3.14×(20÷2)2×15-
3.14×(20÷2)2×10=1570(cm3)
答:石块的体积是1570cm3。
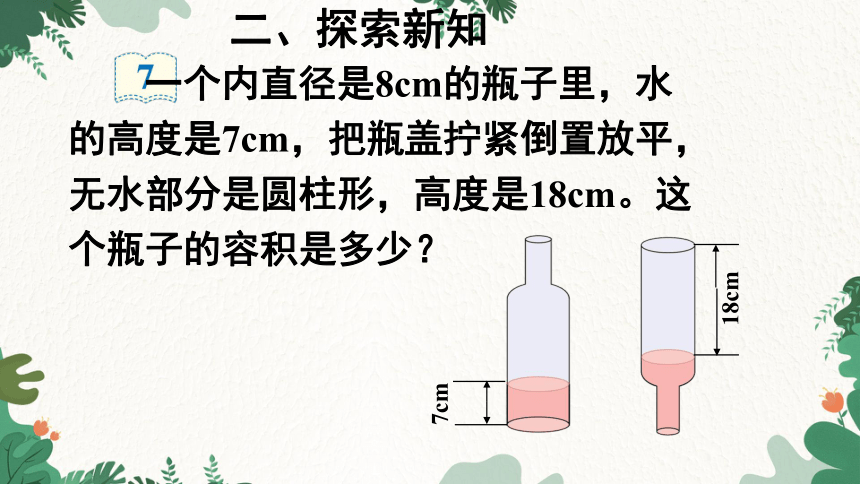
二、探索新知
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
阅读与理解
这个瓶子不是一个完整的圆柱,无法直接计算容积。
能不能转化成圆柱呢?
瓶子里水的体积倒置后,体积没变。
水的体积加上18cm高圆柱的体积就是瓶子的容积。
分析与解答
也就是把瓶子的容积转化成两个圆柱的体积。
答:这个瓶子的容积是1256mL。
瓶子的容积:=3.14×(8÷2)2×7+
3.14×(8÷2)2×18
=3.14×16×(7+18)
=3.14×16×25
=1256 (cm )
=1256(mL)
回顾与反思
我们利用了体积不变的特性,把不规则图形转化成规则图形来计算。
在五年级计算梨的体积也是用了转化的方法。
达标检测
1.一个输液瓶中装有100mL药液,每分钟输2.5mL,下面是12分钟后输液瓶内剩余的药液,请你求出整个输液瓶的容积。
2.5×12=30(mL)
100-30+80=150(mL)
答:整个输液瓶的容积是150mL。
2.有一饮料瓶的容积是1.5升,现在它里面装有一些饮料,正放时饮料高度是15厘米,倒放时空余部分高度为5厘米,问瓶内现有饮料多少升?
1.5升=1500立方厘米
1500÷(15+5)=75(平方厘米)
75×15=1125(立方厘米)=1.125(升)
答:瓶内现有饮料1.125升。
三、巩固提高
做 一 做
1.一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
10cm
10cm
3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(cm )
=282.6(mL)
2.明明家里来了两位小客人,妈妈冲了800mL果汁。如果用右图中的玻璃杯喝果汁,够明明和客人每人一杯吗?
3.14×(6÷2)2×11
=310.86(mL)
800÷310.86≈2.57
2.57<3
答:不够明明和客人每人一杯。
四、课堂小结
水的体积
瓶子的容积
18cm高圆柱的体积
+
=
不规则图形
规则图形
五、课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
六、教学反思
本节课是在学生学习了圆柱的体积计算方法的基础上进行的。教学立足于促进学生的发展,紧密联系生活实际,在教学上主要体现以下几点:
1.加强数学知识与实际生活的联系,提高学生运用数学知识解决实际问题的能力。
2.加强学生在观察、思考、讨论、辨析中对空间与图形问题的思考,利用体积不变的特性,把不规则图形转化成规则图形来计算,渗透转化思想。
解 决 问 题
学习目标
1.通过把不规则形状的体积转化成规则形状,把未知知识转化为已学知识,发现转化过程中的“变”与“不变”,提高学生分析问题和解决问题的能力。
2.渗透等积变形的思想,提高学生的学习兴趣。
学习重点
学习难点
求不规则物体的体积。
用转化法解决不规则物体的容积问题。
一、引入新课
目前为止,我们学会了计算长方体、正方体和圆柱的体积。
S长方体=abh
S正方体=a3
S圆柱=πr2h
还记得我们是怎样测出这个石块的体积的吗?
3.14×(20÷2)2×15-
3.14×(20÷2)2×10=1570(cm3)
答:石块的体积是1570cm3。
二、探索新知
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
阅读与理解
这个瓶子不是一个完整的圆柱,无法直接计算容积。
能不能转化成圆柱呢?
瓶子里水的体积倒置后,体积没变。
水的体积加上18cm高圆柱的体积就是瓶子的容积。
分析与解答
也就是把瓶子的容积转化成两个圆柱的体积。
答:这个瓶子的容积是1256mL。
瓶子的容积:=3.14×(8÷2)2×7+
3.14×(8÷2)2×18
=3.14×16×(7+18)
=3.14×16×25
=1256 (cm )
=1256(mL)
回顾与反思
我们利用了体积不变的特性,把不规则图形转化成规则图形来计算。
在五年级计算梨的体积也是用了转化的方法。
达标检测
1.一个输液瓶中装有100mL药液,每分钟输2.5mL,下面是12分钟后输液瓶内剩余的药液,请你求出整个输液瓶的容积。
2.5×12=30(mL)
100-30+80=150(mL)
答:整个输液瓶的容积是150mL。
2.有一饮料瓶的容积是1.5升,现在它里面装有一些饮料,正放时饮料高度是15厘米,倒放时空余部分高度为5厘米,问瓶内现有饮料多少升?
1.5升=1500立方厘米
1500÷(15+5)=75(平方厘米)
75×15=1125(立方厘米)=1.125(升)
答:瓶内现有饮料1.125升。
三、巩固提高
做 一 做
1.一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
10cm
10cm
3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(cm )
=282.6(mL)
2.明明家里来了两位小客人,妈妈冲了800mL果汁。如果用右图中的玻璃杯喝果汁,够明明和客人每人一杯吗?
3.14×(6÷2)2×11
=310.86(mL)
800÷310.86≈2.57
2.57<3
答:不够明明和客人每人一杯。
四、课堂小结
水的体积
瓶子的容积
18cm高圆柱的体积
+
=
不规则图形
规则图形
五、课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
六、教学反思
本节课是在学生学习了圆柱的体积计算方法的基础上进行的。教学立足于促进学生的发展,紧密联系生活实际,在教学上主要体现以下几点:
1.加强数学知识与实际生活的联系,提高学生运用数学知识解决实际问题的能力。
2.加强学生在观察、思考、讨论、辨析中对空间与图形问题的思考,利用体积不变的特性,把不规则图形转化成规则图形来计算,渗透转化思想。
