5.1.1 变化率问题 课件(34张PPT)
文档属性
| 名称 | 5.1.1 变化率问题 课件(34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-23 17:40:02 | ||
图片预览











文档简介
(共34张PPT)
第五章 一元函数的导数及其应用
[数学文化]——了解数学文化的发展与应用
(一)早期导数概念——特殊的形式
大约在1629年,法国数学家费马研究了作曲线的切线和求函数极值的方法,1637年左右,他写了一篇手稿《求最大值与最小值的方法》.在作切线时,他构造了差分f(A+E)-f(A),发现的因子E就是我们现在所说的导数f′(A).
(二)17世纪——广泛使用的“流数术”
17世纪生产力的发展推动了自然科学和技术的发展,在前人创造性研究的基础上,大数学家牛顿、莱布尼茨等从不同的角度开始系统地研究微积分.牛顿的微积分理论被称为“流数术”,他称变量为流量,称变量的变化率为流数,相当于我们所说的导数.
(三)19世纪导数——逐渐成熟的理论
1823年,柯西在他的《无穷小分析概论》中定义导数:如果函数y=f(x)在变量x的两个给定的界限之间保持连续,并且我们为这样的变量指定一个包含在这两个不同界限之间的值,那么是使变量得到一个无穷小增量.19世纪60年代以后,魏尔斯特拉斯对微积分中出现的各种类型的极限重加表达,导数的定义也就获得了今天常见的形式.
2.我们知道,物体在做曲线运动时,速度的方向是与运动轨迹相切的.例如,如图所示的砂轮打磨下来的微粒,是沿着飞轮的切线飞出去的.这也就意味着,求切线是研究曲线运动时经常要做的事情.
我们在平面解析几何中已知知道怎样求圆锥曲线的切线.不过,可能会让你感到意外的是,那种求切线的方法并不适用于一般的曲线.然而,借助于导数来讨论曲线的切线更具有一般性.
问题1:物体运动的速度和位移有什么关系?加速度和速度又是什么关系呢?
问题2:假设切点为(x0,y0),如何求曲线y=f(x)在点(x0,y0)处的切线方程呢?
链接:: (1)如果从本章我们要学习的导数知识来看的话,上述速度就是位移关于时间的导数,而加速度就是速度关于时间的导数,即v=x′=v0+at,a=v′,
其中x′与v′分别表示x与v对时间t的导数.
(2)由导数的几何意义,切线的斜率为k=f′(x0),则曲线y=f(x)在点(x0,y0)处切线的方程为y-y0=f′(x0)(x-x0).
5.1 导数的概念及其意义
5.1.1 变化率问题
课标要求 素养要求
1.通过实例分析,经历由平均变化率过渡到瞬时变化率的过程.
2.体会极限思想. 根据具体的实例计算平均变化率和瞬时变化率,并得到二者的关系,借此发展数学抽象与数学运算素养.
新知探究
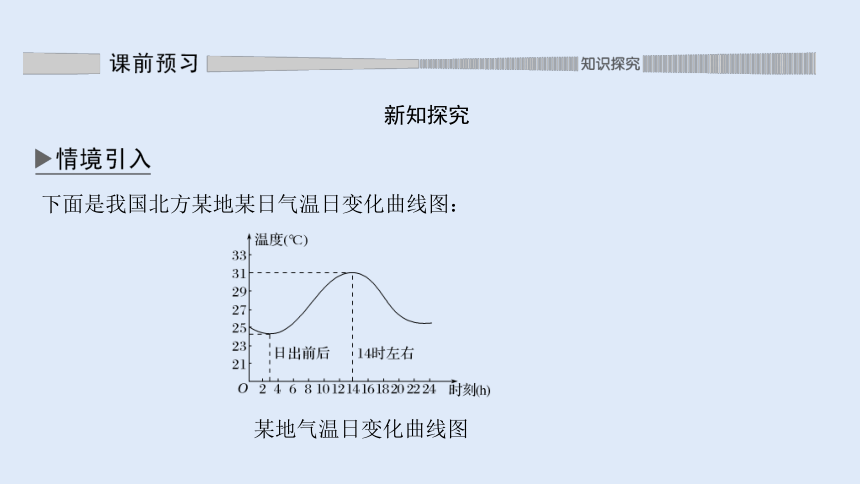
下面是我国北方某地某日气温日变化曲线图:
某地气温日变化曲线图
问题1 从图中可以看出,从6时到10时为“气温陡增”的时段,它的数学意义是什么?
提示 “气温陡增”是指温度在相同的时间内变化大,即温差大.
问题2 如何比较不同时间段内的气温变化的大小?例如:假设6时的气温是25 ℃,10时的气温是29 ℃,12时的气温是30 ℃,那么如何比较从6时到10时与从10时到12时气温变化的大小?
1.瞬时速度
(1)瞬时速度:物体在某一时刻的速度称为瞬时速度.
2.曲线的割线和
切线
切线是割线的极限位置
拓展深化
[微判断]
1.在计算物体运动的瞬时速度时,h(t0+Δt)>h(t0).( )
提示 也可能有h(t0+Δt)≤h(t0).
2.瞬时速度是刻画物体在区间[t0,t0+Δt](Δt>0)上变化快慢的物理量.( )
提示 瞬时速度是刻画物体在某一时刻速度的物理量.
3.曲线在某点处的切线是过该点的割线的极限位置.( )
×
×
√
[微训练]
1.若一质点的运动方程为s=t2+1,则在时间段[1,2]中的平均速度是________.
2.抛物线y=x2+1在点(1,2)处的切线的斜率是________.
答案 2
[微思考]
1.教材中求抛物线切线的斜率的过程中Δx表示什么?它的取值范围是什么?
提示 Δx是自变量的增量,它可以是正值,也可以是负值,但不为0.
2.如果某物体在某时间段内的平均速度为0,能否判定该物体在此时间段内的瞬时速度都为0
提示 不能.
答案 B
题型二 求瞬时速度
【例2】 某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数s(t)=t2+t+1表示,求物体在t=1 s时的瞬时速度.
即物体在t=1 s时的瞬时速度为3 m/s.
【迁移1】 若本例中的条件不变,试求物体的初速度.
解 求物体的初速度,即求物体在t=0时的瞬时速度,
即物体的初速度为1 m/s.
【迁移2】 若本例中的条件不变,试问物体在哪一时刻的瞬时速度为9 m/s.
解 设物体在t0时刻的瞬时速度为9 m/s.
则2t0+1=9,∴t0=4.
则物体在4 s时的瞬时速度为9 m/s.
【训练2】 一质点M按运动方程s(t)=at2+1做直线运动(位移单位:m,时间单位:s),若质点M在t=2 s时的瞬时速度为8 m/s,求常数a的值.
解 质点M在t=2时的瞬时速度即为函数在t=2处的瞬时变化率.
题型三 求曲线在某点处切线的斜率或方程
【例3】 求抛物线f(x)=x2-2x+3在点(1,2)处的切线方程.
规律方法 求抛物线在某点处的切线方程的步骤
【训练3】 求抛物线f(x)=x2-x在点(2,2)处的切线方程.
二、素养训练
1.某质点的运动方程为s(t)=1-t2,则该物体在[1,2]内的平均速度为( )
A.2 B.3 C.-2 D.-3
答案 D
2.一个物体做直线运动,位移s与时间t之间的函数关系式为s(t)=t2+2t+3,则该物体在t=2时的瞬时速度为( )
A.4 B.5 C.6 D.7
答案 C
3.抛物线y=x2+4在点(1,5)处的切线的斜率为________.
答案 2
4.求抛物线f(x)=3x2-4x-1在点(2,3)处的切线方程.
再见
第五章 一元函数的导数及其应用
[数学文化]——了解数学文化的发展与应用
(一)早期导数概念——特殊的形式
大约在1629年,法国数学家费马研究了作曲线的切线和求函数极值的方法,1637年左右,他写了一篇手稿《求最大值与最小值的方法》.在作切线时,他构造了差分f(A+E)-f(A),发现的因子E就是我们现在所说的导数f′(A).
(二)17世纪——广泛使用的“流数术”
17世纪生产力的发展推动了自然科学和技术的发展,在前人创造性研究的基础上,大数学家牛顿、莱布尼茨等从不同的角度开始系统地研究微积分.牛顿的微积分理论被称为“流数术”,他称变量为流量,称变量的变化率为流数,相当于我们所说的导数.
(三)19世纪导数——逐渐成熟的理论
1823年,柯西在他的《无穷小分析概论》中定义导数:如果函数y=f(x)在变量x的两个给定的界限之间保持连续,并且我们为这样的变量指定一个包含在这两个不同界限之间的值,那么是使变量得到一个无穷小增量.19世纪60年代以后,魏尔斯特拉斯对微积分中出现的各种类型的极限重加表达,导数的定义也就获得了今天常见的形式.
2.我们知道,物体在做曲线运动时,速度的方向是与运动轨迹相切的.例如,如图所示的砂轮打磨下来的微粒,是沿着飞轮的切线飞出去的.这也就意味着,求切线是研究曲线运动时经常要做的事情.
我们在平面解析几何中已知知道怎样求圆锥曲线的切线.不过,可能会让你感到意外的是,那种求切线的方法并不适用于一般的曲线.然而,借助于导数来讨论曲线的切线更具有一般性.
问题1:物体运动的速度和位移有什么关系?加速度和速度又是什么关系呢?
问题2:假设切点为(x0,y0),如何求曲线y=f(x)在点(x0,y0)处的切线方程呢?
链接:: (1)如果从本章我们要学习的导数知识来看的话,上述速度就是位移关于时间的导数,而加速度就是速度关于时间的导数,即v=x′=v0+at,a=v′,
其中x′与v′分别表示x与v对时间t的导数.
(2)由导数的几何意义,切线的斜率为k=f′(x0),则曲线y=f(x)在点(x0,y0)处切线的方程为y-y0=f′(x0)(x-x0).
5.1 导数的概念及其意义
5.1.1 变化率问题
课标要求 素养要求
1.通过实例分析,经历由平均变化率过渡到瞬时变化率的过程.
2.体会极限思想. 根据具体的实例计算平均变化率和瞬时变化率,并得到二者的关系,借此发展数学抽象与数学运算素养.
新知探究
下面是我国北方某地某日气温日变化曲线图:
某地气温日变化曲线图
问题1 从图中可以看出,从6时到10时为“气温陡增”的时段,它的数学意义是什么?
提示 “气温陡增”是指温度在相同的时间内变化大,即温差大.
问题2 如何比较不同时间段内的气温变化的大小?例如:假设6时的气温是25 ℃,10时的气温是29 ℃,12时的气温是30 ℃,那么如何比较从6时到10时与从10时到12时气温变化的大小?
1.瞬时速度
(1)瞬时速度:物体在某一时刻的速度称为瞬时速度.
2.曲线的割线和
切线
切线是割线的极限位置
拓展深化
[微判断]
1.在计算物体运动的瞬时速度时,h(t0+Δt)>h(t0).( )
提示 也可能有h(t0+Δt)≤h(t0).
2.瞬时速度是刻画物体在区间[t0,t0+Δt](Δt>0)上变化快慢的物理量.( )
提示 瞬时速度是刻画物体在某一时刻速度的物理量.
3.曲线在某点处的切线是过该点的割线的极限位置.( )
×
×
√
[微训练]
1.若一质点的运动方程为s=t2+1,则在时间段[1,2]中的平均速度是________.
2.抛物线y=x2+1在点(1,2)处的切线的斜率是________.
答案 2
[微思考]
1.教材中求抛物线切线的斜率的过程中Δx表示什么?它的取值范围是什么?
提示 Δx是自变量的增量,它可以是正值,也可以是负值,但不为0.
2.如果某物体在某时间段内的平均速度为0,能否判定该物体在此时间段内的瞬时速度都为0
提示 不能.
答案 B
题型二 求瞬时速度
【例2】 某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数s(t)=t2+t+1表示,求物体在t=1 s时的瞬时速度.
即物体在t=1 s时的瞬时速度为3 m/s.
【迁移1】 若本例中的条件不变,试求物体的初速度.
解 求物体的初速度,即求物体在t=0时的瞬时速度,
即物体的初速度为1 m/s.
【迁移2】 若本例中的条件不变,试问物体在哪一时刻的瞬时速度为9 m/s.
解 设物体在t0时刻的瞬时速度为9 m/s.
则2t0+1=9,∴t0=4.
则物体在4 s时的瞬时速度为9 m/s.
【训练2】 一质点M按运动方程s(t)=at2+1做直线运动(位移单位:m,时间单位:s),若质点M在t=2 s时的瞬时速度为8 m/s,求常数a的值.
解 质点M在t=2时的瞬时速度即为函数在t=2处的瞬时变化率.
题型三 求曲线在某点处切线的斜率或方程
【例3】 求抛物线f(x)=x2-2x+3在点(1,2)处的切线方程.
规律方法 求抛物线在某点处的切线方程的步骤
【训练3】 求抛物线f(x)=x2-x在点(2,2)处的切线方程.
二、素养训练
1.某质点的运动方程为s(t)=1-t2,则该物体在[1,2]内的平均速度为( )
A.2 B.3 C.-2 D.-3
答案 D
2.一个物体做直线运动,位移s与时间t之间的函数关系式为s(t)=t2+2t+3,则该物体在t=2时的瞬时速度为( )
A.4 B.5 C.6 D.7
答案 C
3.抛物线y=x2+4在点(1,5)处的切线的斜率为________.
答案 2
4.求抛物线f(x)=3x2-4x-1在点(2,3)处的切线方程.
再见
