5.2.1 基本初等函数的导数 课件(共31张PPT)
文档属性
| 名称 | 5.2.1 基本初等函数的导数 课件(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-23 17:45:26 | ||
图片预览










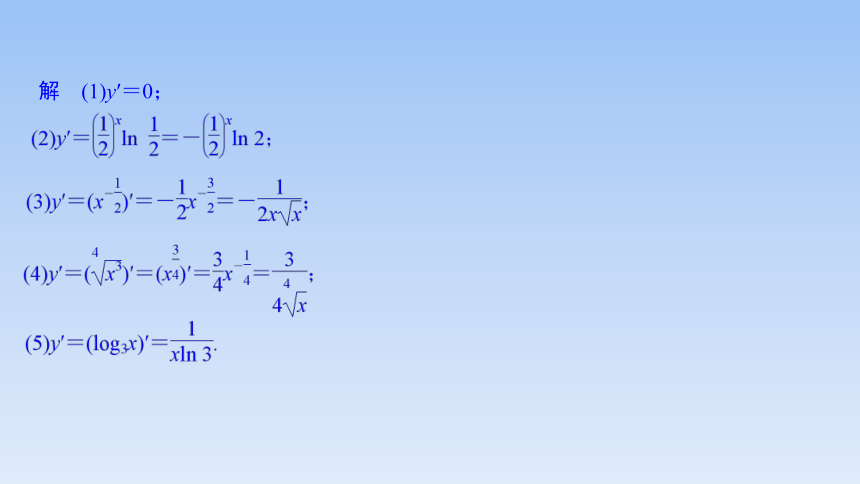
文档简介
(共31张PPT)
5.2 导数的运算
5.2.1 基本初等函数的导数
新知探究
问题2 函数(2)(3)(4)(5)的导数分别是什么?
问题3 函数(2)(3)(5)均可表示为y=xα(α∈Q*)的形式,其导数有何规律?
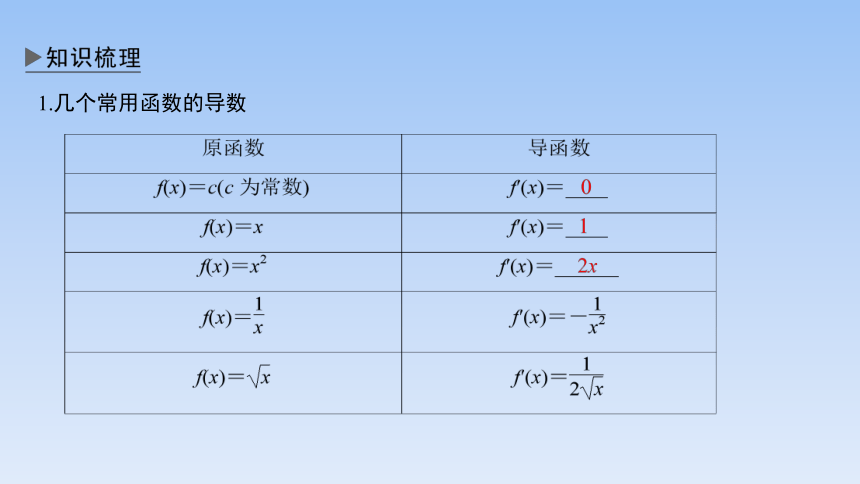
1.几个常用函数的导数
2.基本初等函数的导数公式
×
√
×
提示 若f(x)=4x,则f′(x)=4xln 4.
[微训练]
1.已知f(x)=x2,则f′(3)等于( )
A.0 B.2x
C.6 D.9
解析 ∵f(x)=x2,∴f′(x)=2x,∴f′(3)=6.
答案 C
2.求下列函数的导数:
题型一 利用导数公式求函数的导数
【例1】 求下列函数的导数:
解 (1)y′=0;
规律方法 求简单函数的导函数的基本方法:
(1)用导数的定义求导,但运算比较繁琐;
(2)用导数公式求导,可以简化运算过程,降低运算难度.解题时根据所给问题的特征,将题中函数的结构进行调整,再选择合适的求导公式.
【训练1】 求下列函数的导数:
题型二 利用导数公式解决切线问题
角度1 求切线的方程
答案 B
角度2 求参数值
【例2-2】 已知y=kx是曲线y=ln x的一条切线,则k=________.
角度3 曲线上的点到直线的最小距离问题
【例2-3】 设P是曲线y=ex上任意一点,求点P到直线y=x的最小距离.
解 如图,设l是与直线y=x平行,且与曲线y=ex相切的直线,则切点到直线y=x的距离最小.
设直线l与曲线y=ex相切于点P(x0,y0).
因为y′=ex,所以ex0=1,所以x0=0.
代入y=ex,得y0=1,所以P(0,1).
规律方法 利用导数的几何意义解决切线问题的两种情况
(1)若已知点是切点,则在该点处的切线斜率就是该点处的导数.
(2)如果已知点不是切点,则应先设出切点,再借助两点连线的斜率公式进行求解.
解 (1)设所求切线的斜率为k.
(2)设切点坐标为(x0,y0).
即4x-y-1-ln 4=0.
题型三 导数公式的实际应用
【例3】 某城市近10年间房价年均上涨率为10%,房价p(单位:万元)与时间t(单位:年)有如下函数关系:p(t)=p0(1+10%)t,假定p0=1,那么在第5个年头,房价上涨的速度大约是多少(精确0.01万元/年)?(参考数据:1.15=1.611,ln 1.1=0.095)
解 由题意得p′(t)=1.1tln 1.1
所以p′(5)=1.15ln 1.1≈1.611×0.095≈0.15(万元/年)
所以在第5个年头,该市房价上涨的速度大约是0.15万元/年.
规律方法 由导数的定义可知,导数是瞬时变化率,所以求某个量的变化速度,就是求相关函数在某点处的导数.
【训练3】 从时刻t=0开始的t(s)内,通过某导体的电量(单位:库仑)可以由公式q=cos t表示.
求第5秒和第7秒时的电流强度(单位:安)
解 由q=cos t得q′=-sin t,
所以q′(5)=-sin 5,q′(7)=-sin 7,
即第5秒,第7秒时的电流强度分别是-sin 5安,-sin 7安.
一、素养落地
1.通过学习导数公式及应用导数公式求基本初等函数的导数,提升数学运算素养.
2.利用常见函数的导数公式可以比较简捷的求出函数的导数,其关键是牢记和运用好导数公式.解题时,能认真观察函数的结构特征,积极地进行联想化归.
二、素养训练
1.函数y=xe的导数是( )
A.y′=xe B.y′=exe-1
C.y′=exe D.y′=ln x
解析 由(xα)′=αxα-1得,y′=exe-1.
答案 B
答案 D
3.已知f(x)=x2,g(x)=x.若m满足f′(m)+g′(m)=3,则m的值为________.
解析 f′(x)+g′(x)=2x+1,f′(m)+g′(m)=2m+1=3,故m=1.
答案 1
答案 x+9y-6=0
5.曲线y=ex在点(2,e2)处的切线与坐标轴所围三角形的面积为________.
解析 ∵y′=(ex)′=ex,∴在点(2,e2)处的切线斜率为k=e2,
∴曲线在点(2,e2)处的切线方程为y-e2=e2(x-2),
即y=e2x-e2.当x=0时,y=-e2,当y=0时,x=1.
5.2 导数的运算
5.2.1 基本初等函数的导数
新知探究
问题2 函数(2)(3)(4)(5)的导数分别是什么?
问题3 函数(2)(3)(5)均可表示为y=xα(α∈Q*)的形式,其导数有何规律?
1.几个常用函数的导数
2.基本初等函数的导数公式
×
√
×
提示 若f(x)=4x,则f′(x)=4xln 4.
[微训练]
1.已知f(x)=x2,则f′(3)等于( )
A.0 B.2x
C.6 D.9
解析 ∵f(x)=x2,∴f′(x)=2x,∴f′(3)=6.
答案 C
2.求下列函数的导数:
题型一 利用导数公式求函数的导数
【例1】 求下列函数的导数:
解 (1)y′=0;
规律方法 求简单函数的导函数的基本方法:
(1)用导数的定义求导,但运算比较繁琐;
(2)用导数公式求导,可以简化运算过程,降低运算难度.解题时根据所给问题的特征,将题中函数的结构进行调整,再选择合适的求导公式.
【训练1】 求下列函数的导数:
题型二 利用导数公式解决切线问题
角度1 求切线的方程
答案 B
角度2 求参数值
【例2-2】 已知y=kx是曲线y=ln x的一条切线,则k=________.
角度3 曲线上的点到直线的最小距离问题
【例2-3】 设P是曲线y=ex上任意一点,求点P到直线y=x的最小距离.
解 如图,设l是与直线y=x平行,且与曲线y=ex相切的直线,则切点到直线y=x的距离最小.
设直线l与曲线y=ex相切于点P(x0,y0).
因为y′=ex,所以ex0=1,所以x0=0.
代入y=ex,得y0=1,所以P(0,1).
规律方法 利用导数的几何意义解决切线问题的两种情况
(1)若已知点是切点,则在该点处的切线斜率就是该点处的导数.
(2)如果已知点不是切点,则应先设出切点,再借助两点连线的斜率公式进行求解.
解 (1)设所求切线的斜率为k.
(2)设切点坐标为(x0,y0).
即4x-y-1-ln 4=0.
题型三 导数公式的实际应用
【例3】 某城市近10年间房价年均上涨率为10%,房价p(单位:万元)与时间t(单位:年)有如下函数关系:p(t)=p0(1+10%)t,假定p0=1,那么在第5个年头,房价上涨的速度大约是多少(精确0.01万元/年)?(参考数据:1.15=1.611,ln 1.1=0.095)
解 由题意得p′(t)=1.1tln 1.1
所以p′(5)=1.15ln 1.1≈1.611×0.095≈0.15(万元/年)
所以在第5个年头,该市房价上涨的速度大约是0.15万元/年.
规律方法 由导数的定义可知,导数是瞬时变化率,所以求某个量的变化速度,就是求相关函数在某点处的导数.
【训练3】 从时刻t=0开始的t(s)内,通过某导体的电量(单位:库仑)可以由公式q=cos t表示.
求第5秒和第7秒时的电流强度(单位:安)
解 由q=cos t得q′=-sin t,
所以q′(5)=-sin 5,q′(7)=-sin 7,
即第5秒,第7秒时的电流强度分别是-sin 5安,-sin 7安.
一、素养落地
1.通过学习导数公式及应用导数公式求基本初等函数的导数,提升数学运算素养.
2.利用常见函数的导数公式可以比较简捷的求出函数的导数,其关键是牢记和运用好导数公式.解题时,能认真观察函数的结构特征,积极地进行联想化归.
二、素养训练
1.函数y=xe的导数是( )
A.y′=xe B.y′=exe-1
C.y′=exe D.y′=ln x
解析 由(xα)′=αxα-1得,y′=exe-1.
答案 B
答案 D
3.已知f(x)=x2,g(x)=x.若m满足f′(m)+g′(m)=3,则m的值为________.
解析 f′(x)+g′(x)=2x+1,f′(m)+g′(m)=2m+1=3,故m=1.
答案 1
答案 x+9y-6=0
5.曲线y=ex在点(2,e2)处的切线与坐标轴所围三角形的面积为________.
解析 ∵y′=(ex)′=ex,∴在点(2,e2)处的切线斜率为k=e2,
∴曲线在点(2,e2)处的切线方程为y-e2=e2(x-2),
即y=e2x-e2.当x=0时,y=-e2,当y=0时,x=1.
