5.2.3 简单复合函数的导数 课件(共27张PPT)
文档属性
| 名称 | 5.2.3 简单复合函数的导数 课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-23 17:48:08 | ||
图片预览





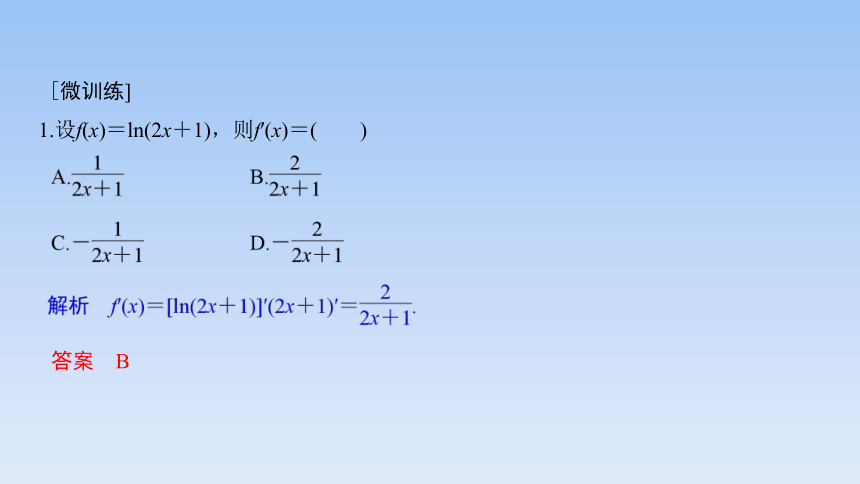



文档简介
(共27张PPT)
5.2.3 简单复合函数的导数
课标要求 素养要求
能求简单的复合函数(限于形如f(ax+b))的导数. 在根据复合函数的求导法则求复合函数的导数的过程中,发展学生的数学运算素养.
新知探究
假设某商品的利润y是销售量u的函数,销售量u是销售价格x的函数,且
y=f(u)=60u-u2,u=g(x)=60-3x,
那么,不难看出,利润y是销售价格x的函数,且有
y=60u-u2=60(60-3x)-(60-3x)2=180x-9x2,
上式也可这样得到
f(g(x))=60g(x)-[g(x)]2=180x-9x2.
问题1 函数f(g(x))与f(x)和g(x)是什么关系?
提示 f(g(x))是f(x)与g(x)的复合函数.
问题2 求f(u)=60u-u2的导数f′(u),u=g(x)=60-3x的导数u′=g′(x).
提示 f′(u)=60-2u=60-2(60-3x)=6x-60,u′=g′(x)=-3.
问题3 设y=f(g(x))=180x-9x2,求y′,并观察f′(u)和u′=g′(x)的关系.
提示 y′=180-18x,易知y′=f′(u) ux′.
1.复合函数的概念
一般地,对于两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作___________.
2.
一般地,对于由函数y=f(u)和u=g(x)复合而成的函数y=f(g(x)),它的导数y=f(u),u=g(x)的导数间的关系为yx′=_________,即y对x的导数等于y对u的导数与u对x的导数的乘积.
y=f(g(x))
yu′·ux′
复合函数的求导法则
正确地拆分复合函数是求导的前提
拓展深化
[微判断]
1.函数f(x)=ln(-2x+1)是由y=ln u与u=-2x+1复合而成的.( )
√
×
提示 f(x)不是复合函数.
3.设f(x)=e-x,则f′(x)=e-x.( )
提示 f′(x)=-e-x.
×
[微训练]
1.设f(x)=ln(2x+1),则f′(x)=( )
答案 B
答案 B
3.曲线f(x)=e-2x+3在(1,f(1))处的切线的斜率是________.
解析 f′(x)=-2e-2x+3,f′(1)=-2e,即k=-2e.
答案 -2e
[微思考]
1.复合函数y=f(g(x)),用中间变量y=f(u),u=g(x)代换后求导的顺序是什么?
提示 根据复合函数的求导法则yx′=yu′·ux′,求导的顺序是从外向内逐层求导.
题型一 求复合函数的导数
【例1】 求下列函数的导数.
(2)设y=log2u,u=2x+1,
则yx′=yu′ux′=(log2u)′(2x+1)′
(3)设y=eu,u=3x+2,
则yx′=y′uu′x=(eu)′·(3x+2)′
=3eu=3e3x+2,
即y′=3e3x+2.
规律方法 (1)求复合函数的导数的步骤
(2)求复合函数的导数的注意点:①分解的函数通常为基本初等函数;②求导时分清是对哪个变量求导;③计算结果尽量简洁.
解 (1)设y=u4,u=2x-1,
则yx′=yu′ux′=(u4)′(2x-1)′=4u3·2=8(2x-1)3.
(2)设y=10u,u=2x+3,
则yx′=yu′ux′=(10u)′(2x+3)′=10uln 10·2=2·102x+3·ln 10=102x+3·ln 100.
(3)yx′=(e-x)′sin 2x+e-x·(sin 2x)′
=-e-xsin 2x+2e-xcos 2x.
规律方法 解此类问题的关键有两个:
(1)求复合函数的导数,这是正确解答的前提条件,要注意把复合函数逐层分解,求导时不要有遗漏.
(2)求切线方程,注意切线所过的点是否为切点.
【训练2】 已知f(x)为偶函数,当x≤0时,f(x)=e-x-1-x,则曲线y=f(x)在点(1,2)处的切线方程是________.
解析 设x>0,则-x<0,f(-x)=ex-1+x.
又f(x)为偶函数,f(x)=f(-x)=ex-1+x.
所以当x>0时,f(x)=ex-1+x.
因此,当x>0时,f′(x)=ex-1+1,f′(1)=e0+1=2.
则曲线y=f(x)在点(1,2)处的切线的斜率为f′(1)=2,
所以切线方程为y-2=2(x-1),即2x-y=0.
答案 2x-y=0
规律方法 将复合函数的求导与导数的实际意义结合,函数在某点处的导数反映了函数在该点的瞬时变化率,体现导数揭示物体在某时刻的变化状况.
【训练3】 已知某质点的位移s与位移时间t满足s=tet-1,则质点在t=1时的瞬时速度为________.
解析 s′=(t+1)et-1,当t=1时,s′(1)=2.
答案 2
一、素养落地
1.通过学习复合函数的求导法则及其简单应用,提升数学运算素养.
2.求复合函数的导数应处理好以下环节:
(1)中间变量的选择应是基本函数结构;
(2)关键是正确分析函数的复合层次;
(3)一般是从最外层开始,由外及里,一层层地求导;
(4)善于把一部分表达式作为一个整体;
(5)最后要把中间变量换成自变量的函数.
二、素养训练
1.设f(x)=sin 2x,则f′(x)=( )
A.cos 2x B.2cos 2x
C.-cos 2x D.-2cos 2x
解析 f′(x)=(sin 2x)′(2x′)=2cos 2x.
答案 B
2.设f(x)=ln(3x+2)-3x2,则f′(0)=( )
答案 B
解析 y=(3x-1)-2,
设y=u-2,u=3x-1,
yx′=yu′ux′=(u-2)′·(3x-1)′
4.设曲线y=eax在点(0,1)处的切线与直线x+2y+1=0垂直,则a=________.
答案 2
5.2.3 简单复合函数的导数
课标要求 素养要求
能求简单的复合函数(限于形如f(ax+b))的导数. 在根据复合函数的求导法则求复合函数的导数的过程中,发展学生的数学运算素养.
新知探究
假设某商品的利润y是销售量u的函数,销售量u是销售价格x的函数,且
y=f(u)=60u-u2,u=g(x)=60-3x,
那么,不难看出,利润y是销售价格x的函数,且有
y=60u-u2=60(60-3x)-(60-3x)2=180x-9x2,
上式也可这样得到
f(g(x))=60g(x)-[g(x)]2=180x-9x2.
问题1 函数f(g(x))与f(x)和g(x)是什么关系?
提示 f(g(x))是f(x)与g(x)的复合函数.
问题2 求f(u)=60u-u2的导数f′(u),u=g(x)=60-3x的导数u′=g′(x).
提示 f′(u)=60-2u=60-2(60-3x)=6x-60,u′=g′(x)=-3.
问题3 设y=f(g(x))=180x-9x2,求y′,并观察f′(u)和u′=g′(x)的关系.
提示 y′=180-18x,易知y′=f′(u) ux′.
1.复合函数的概念
一般地,对于两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作___________.
2.
一般地,对于由函数y=f(u)和u=g(x)复合而成的函数y=f(g(x)),它的导数y=f(u),u=g(x)的导数间的关系为yx′=_________,即y对x的导数等于y对u的导数与u对x的导数的乘积.
y=f(g(x))
yu′·ux′
复合函数的求导法则
正确地拆分复合函数是求导的前提
拓展深化
[微判断]
1.函数f(x)=ln(-2x+1)是由y=ln u与u=-2x+1复合而成的.( )
√
×
提示 f(x)不是复合函数.
3.设f(x)=e-x,则f′(x)=e-x.( )
提示 f′(x)=-e-x.
×
[微训练]
1.设f(x)=ln(2x+1),则f′(x)=( )
答案 B
答案 B
3.曲线f(x)=e-2x+3在(1,f(1))处的切线的斜率是________.
解析 f′(x)=-2e-2x+3,f′(1)=-2e,即k=-2e.
答案 -2e
[微思考]
1.复合函数y=f(g(x)),用中间变量y=f(u),u=g(x)代换后求导的顺序是什么?
提示 根据复合函数的求导法则yx′=yu′·ux′,求导的顺序是从外向内逐层求导.
题型一 求复合函数的导数
【例1】 求下列函数的导数.
(2)设y=log2u,u=2x+1,
则yx′=yu′ux′=(log2u)′(2x+1)′
(3)设y=eu,u=3x+2,
则yx′=y′uu′x=(eu)′·(3x+2)′
=3eu=3e3x+2,
即y′=3e3x+2.
规律方法 (1)求复合函数的导数的步骤
(2)求复合函数的导数的注意点:①分解的函数通常为基本初等函数;②求导时分清是对哪个变量求导;③计算结果尽量简洁.
解 (1)设y=u4,u=2x-1,
则yx′=yu′ux′=(u4)′(2x-1)′=4u3·2=8(2x-1)3.
(2)设y=10u,u=2x+3,
则yx′=yu′ux′=(10u)′(2x+3)′=10uln 10·2=2·102x+3·ln 10=102x+3·ln 100.
(3)yx′=(e-x)′sin 2x+e-x·(sin 2x)′
=-e-xsin 2x+2e-xcos 2x.
规律方法 解此类问题的关键有两个:
(1)求复合函数的导数,这是正确解答的前提条件,要注意把复合函数逐层分解,求导时不要有遗漏.
(2)求切线方程,注意切线所过的点是否为切点.
【训练2】 已知f(x)为偶函数,当x≤0时,f(x)=e-x-1-x,则曲线y=f(x)在点(1,2)处的切线方程是________.
解析 设x>0,则-x<0,f(-x)=ex-1+x.
又f(x)为偶函数,f(x)=f(-x)=ex-1+x.
所以当x>0时,f(x)=ex-1+x.
因此,当x>0时,f′(x)=ex-1+1,f′(1)=e0+1=2.
则曲线y=f(x)在点(1,2)处的切线的斜率为f′(1)=2,
所以切线方程为y-2=2(x-1),即2x-y=0.
答案 2x-y=0
规律方法 将复合函数的求导与导数的实际意义结合,函数在某点处的导数反映了函数在该点的瞬时变化率,体现导数揭示物体在某时刻的变化状况.
【训练3】 已知某质点的位移s与位移时间t满足s=tet-1,则质点在t=1时的瞬时速度为________.
解析 s′=(t+1)et-1,当t=1时,s′(1)=2.
答案 2
一、素养落地
1.通过学习复合函数的求导法则及其简单应用,提升数学运算素养.
2.求复合函数的导数应处理好以下环节:
(1)中间变量的选择应是基本函数结构;
(2)关键是正确分析函数的复合层次;
(3)一般是从最外层开始,由外及里,一层层地求导;
(4)善于把一部分表达式作为一个整体;
(5)最后要把中间变量换成自变量的函数.
二、素养训练
1.设f(x)=sin 2x,则f′(x)=( )
A.cos 2x B.2cos 2x
C.-cos 2x D.-2cos 2x
解析 f′(x)=(sin 2x)′(2x′)=2cos 2x.
答案 B
2.设f(x)=ln(3x+2)-3x2,则f′(0)=( )
答案 B
解析 y=(3x-1)-2,
设y=u-2,u=3x-1,
yx′=yu′ux′=(u-2)′·(3x-1)′
4.设曲线y=eax在点(0,1)处的切线与直线x+2y+1=0垂直,则a=________.
答案 2
