第五章一元函数的导数及其应用 章末复习课 课件(共31张PPT)
文档属性
| 名称 | 第五章一元函数的导数及其应用 章末复习课 课件(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-23 17:53:02 | ||
图片预览











文档简介
(共31张PPT)
章末复习课
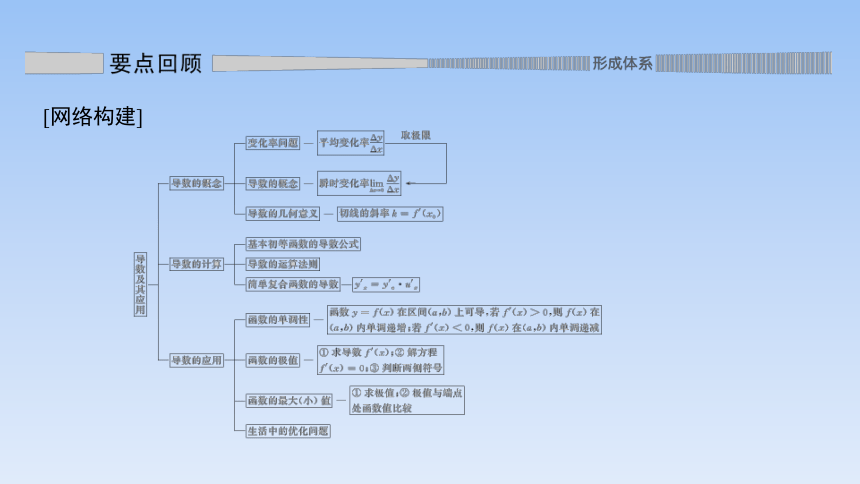
[网络构建]
2.曲线的切线方程
利用导数求曲线过点P的切线方程时应注意:
(1)判断P点是否在曲线上;
(2)如果曲线y=f(x)在P(x0,f(x0))处的切线平行于y轴(此时导数不存在),可得方程为x=x0;P点坐标适合切线方程,如果切线不平行于y轴,P点处的切线斜率为f′(x0).
3.利用基本初等函数的求导公式和四则运算法则求导数,熟记基本求导公式,熟练运用法则是关键,有时先化简再求导,会给解题带来方便.因此观察式子的特点,对式子进行适当的变形是优化解题过程的关键.
4.函数的单调性与导数
(1)在利用导数讨论函数的单调区间时,首先要确定函数的定义域,解决问题的过程中,只能在函数的定义域内,通过讨论导数的符号,来判断函数的单调区间;
(2)注意在某一区间内f′(x)>0(或f′(x)<0)是函数f(x)在该区间上为增(或减)函数的充分条件.
5.利用导数研究函数的极值要注意
(1)极值是一个局部概念,是仅对某一点的左右两侧邻近区域而言的.
(2)连续函数f(x)在其定义域上的极值点可能不止一个,也可能没有极值点,函数的极大值与极小值没有必然的大小联系,函数的一个极小值也不一定比它的一个极大值小.
(3)可导函数的极值点一定是导数为零的点,但函数的导数为零的点,不一定是该函数的极值点.因此导数为零的点仅是该点为极值点的必要条件,其充要条件是加上这点两侧的导数异号.
6.求函数的最大值与最小值
(1)函数的最大值与最小值:在闭区间[a,b]上连续的函数f(x),在[a,b]上必有最大值与最小值;但在开区间(a,b)内连续的函数f(x)不一定有最大值与最小值,例如:f(x)=x3,x∈(-1,1).
(2)求函数最值的步骤
一般地,求函数y=f(x)在[a,b]上最大值与最小值的步骤如下:
①求函数y=f(x)在(a,b)内的极值;
②将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
7.应用导数解决实际问题,关键在于建立恰当的数学模型(函数关系),如果函数在区间内只有一个点x0,使f′(x0)=0,则f(x0)是函数的最值.
要点一 导数的几何意义及应用
导数几何意义的应用,主要体现在与切线方程有关的问题上.利用导数的几何意义求切线方程的关键是弄清楚所给的点是不是切点,常见类型有两种:一种是求“在某点处的切线方程”,此点一定为切点,先求导,再求斜率,进而求出切线方程;另一种是求“过某点的切线方程”,这种类型中的点不一定是切点,可先设切点为Q(x1,y1),则切线方程为y-y1=f′(x1)(x-x1),再由切线过点P(x0,y0)得y0-y1=f′(x1)(x0-x1).①
又已知y1=f(x1)②
由①②求出x1,y1的值,即求出了过点P(x0,y0)的切线方程.
切线问题是高考的热点内容之一,在高考试题中既有选择题、填空题,也有综合性大题,难度一般为中等.
令x=0,得y=1,即直线l在y轴上的截距为1.
(2)由y′=ex,知曲线y=ex在点(0,1)处的切线斜率k1=e0=1.
依题意k1k2=-1,所以m=1,从而n=1.
则点P的坐标为(1,1).
答案 (1)1 (2)(1,1)
答案 2x+y+1=0
要点二 应用导数求函数的单调区间
在区间(a,b)内,如果f′(x)>0,那么函数y=f(x)在区间(a,b)内单调递增;在区间(a,b)内,如果f′(x)<0,那么函数y=f(x)在区间(a,b)内单调递减.
设g(x)=x2-ax+2,二次方程g(x)=0的判别式Δ=a2-8.
当x变化时,f′(x)、f(x)的变化情况如下表:
【训练2】 已知函数f(x)=ln x+a(1-x),讨论f(x)的单调性.
要点三 利用导数求函数的极值和最值
1.利用导数求函数极值的一般步骤
(1)确定函数f(x)的定义域;
(2)解方程f′(x)=0的根;
(3)检验f′(x)=0的根的两侧f′(x)的符号.
若左正右负,则f(x)在此根处取得极大值;
若左负右正,则f(x)在此根处取得极小值;
否则,此根不是f(x)的极值点.
2.求函数f(x)在闭区间[a,b]上的最大值、最小值的方法与步骤
(1)求f(x)在(a,b)内的极值;
(2)将(1)求得的极值与f(a)、f(b)相比较,其中最大的一个值为最大值,最小的一个值为最小值.
特别地,①当f(x)在[a,b]上单调时,其最小值、最大值在区间端点取得;②当f(x)在(a,b)内只有一个极值点时,若在这一点处f(x)有极大(或极小)值,则可以断定f(x)在该点处取得最大(最小)值, 这里(a,b)也可以是(-∞,+∞).
(1)求函数y=f(x)在x=-2时对应的切线方程;
(2)求函数y=f(x)在[-2,1]上的最大值与最小值.
解 (1)f′(x)=-3x2+2ax+b,
当x=-2时,f(-2)=2,即切点为(-2,2).
又因为切线斜率k=f′(-2)=-8,
所以,所求切线方程为y-2=-8(x+2),即8x+y+14=0.
(2)当x变化时,f′(x),f(x)的变化情况如下表:
(1)当a=-2时,求函数f(x)的极大值;
(2)若函数f(x)有极大值,求实数a的取值范围.
解 (1)因为a=-2,所以f′(x)=1-2sin x.
(2)f′(x)=1+asin x.
①当|a|≤1时,|asin x|<1,
所以f(x)在x=β处取得极大值.
综上所述,实数a的取值范围是(-∞,-1).
要点四 导数与函数、不等式的综合应用
利用导数研究函数是高考的必考内容,也是高考的重点、热点.考题利用导数作为工具,考查求函数的单调区间、函数的极值与最值,参数的取值范围等问题,若以选择题、填空题出现,以中低档题为主;若以解答题形式出现,则难度以中档以上为主,有时也以压轴题的形式出现.考查中常渗透函数、不等式等有关知识,综合性较强.
【例4】 已知函数f(x)=xln x.
(1)求f(x)的最小值;
(2)若对所有x≥1都有f(x)≥ax-1,求实数a的取值范围;
(3)若关于x的方程f(x)=b恰有两个不相等的实数根,求实数b的取值范围.
解 (1)f(x)的定义域是(0,+∞),f′(x)=1+ln x,
(2)∵f(x)=xln x,
当x≥1时,f(x)≥ax-1恒成立,
等价于xln x≥ax-1(x≥1)恒成立,
∴g(x)在[1,+∞)上单调递增,∴g(x)min=g(1)=1,
∴a≤1,即实数a的取值范围为(-∞,1].
(3)若关于x的方程f(x)=b恰有两个不相等的实数根,即y=b的图象和y=f(x)的图象在(0,+∞)上有两个不同的交点,
(1)若对任意实数x,f′(x)≥m恒成立,求m的最大值;
(2)若函数f(x)恰有一个零点,求a的取值范围.
(2)f′(x)=3x2-9x+6=3(x-2)(x-1),
由f′(x)>0 x>2或x<1,由f′(x)<0 1∴f(x)在(-∞,1)和(2,+∞)上单调递增,在(1,2)上单调递减,
章末复习课
[网络构建]
2.曲线的切线方程
利用导数求曲线过点P的切线方程时应注意:
(1)判断P点是否在曲线上;
(2)如果曲线y=f(x)在P(x0,f(x0))处的切线平行于y轴(此时导数不存在),可得方程为x=x0;P点坐标适合切线方程,如果切线不平行于y轴,P点处的切线斜率为f′(x0).
3.利用基本初等函数的求导公式和四则运算法则求导数,熟记基本求导公式,熟练运用法则是关键,有时先化简再求导,会给解题带来方便.因此观察式子的特点,对式子进行适当的变形是优化解题过程的关键.
4.函数的单调性与导数
(1)在利用导数讨论函数的单调区间时,首先要确定函数的定义域,解决问题的过程中,只能在函数的定义域内,通过讨论导数的符号,来判断函数的单调区间;
(2)注意在某一区间内f′(x)>0(或f′(x)<0)是函数f(x)在该区间上为增(或减)函数的充分条件.
5.利用导数研究函数的极值要注意
(1)极值是一个局部概念,是仅对某一点的左右两侧邻近区域而言的.
(2)连续函数f(x)在其定义域上的极值点可能不止一个,也可能没有极值点,函数的极大值与极小值没有必然的大小联系,函数的一个极小值也不一定比它的一个极大值小.
(3)可导函数的极值点一定是导数为零的点,但函数的导数为零的点,不一定是该函数的极值点.因此导数为零的点仅是该点为极值点的必要条件,其充要条件是加上这点两侧的导数异号.
6.求函数的最大值与最小值
(1)函数的最大值与最小值:在闭区间[a,b]上连续的函数f(x),在[a,b]上必有最大值与最小值;但在开区间(a,b)内连续的函数f(x)不一定有最大值与最小值,例如:f(x)=x3,x∈(-1,1).
(2)求函数最值的步骤
一般地,求函数y=f(x)在[a,b]上最大值与最小值的步骤如下:
①求函数y=f(x)在(a,b)内的极值;
②将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
7.应用导数解决实际问题,关键在于建立恰当的数学模型(函数关系),如果函数在区间内只有一个点x0,使f′(x0)=0,则f(x0)是函数的最值.
要点一 导数的几何意义及应用
导数几何意义的应用,主要体现在与切线方程有关的问题上.利用导数的几何意义求切线方程的关键是弄清楚所给的点是不是切点,常见类型有两种:一种是求“在某点处的切线方程”,此点一定为切点,先求导,再求斜率,进而求出切线方程;另一种是求“过某点的切线方程”,这种类型中的点不一定是切点,可先设切点为Q(x1,y1),则切线方程为y-y1=f′(x1)(x-x1),再由切线过点P(x0,y0)得y0-y1=f′(x1)(x0-x1).①
又已知y1=f(x1)②
由①②求出x1,y1的值,即求出了过点P(x0,y0)的切线方程.
切线问题是高考的热点内容之一,在高考试题中既有选择题、填空题,也有综合性大题,难度一般为中等.
令x=0,得y=1,即直线l在y轴上的截距为1.
(2)由y′=ex,知曲线y=ex在点(0,1)处的切线斜率k1=e0=1.
依题意k1k2=-1,所以m=1,从而n=1.
则点P的坐标为(1,1).
答案 (1)1 (2)(1,1)
答案 2x+y+1=0
要点二 应用导数求函数的单调区间
在区间(a,b)内,如果f′(x)>0,那么函数y=f(x)在区间(a,b)内单调递增;在区间(a,b)内,如果f′(x)<0,那么函数y=f(x)在区间(a,b)内单调递减.
设g(x)=x2-ax+2,二次方程g(x)=0的判别式Δ=a2-8.
当x变化时,f′(x)、f(x)的变化情况如下表:
【训练2】 已知函数f(x)=ln x+a(1-x),讨论f(x)的单调性.
要点三 利用导数求函数的极值和最值
1.利用导数求函数极值的一般步骤
(1)确定函数f(x)的定义域;
(2)解方程f′(x)=0的根;
(3)检验f′(x)=0的根的两侧f′(x)的符号.
若左正右负,则f(x)在此根处取得极大值;
若左负右正,则f(x)在此根处取得极小值;
否则,此根不是f(x)的极值点.
2.求函数f(x)在闭区间[a,b]上的最大值、最小值的方法与步骤
(1)求f(x)在(a,b)内的极值;
(2)将(1)求得的极值与f(a)、f(b)相比较,其中最大的一个值为最大值,最小的一个值为最小值.
特别地,①当f(x)在[a,b]上单调时,其最小值、最大值在区间端点取得;②当f(x)在(a,b)内只有一个极值点时,若在这一点处f(x)有极大(或极小)值,则可以断定f(x)在该点处取得最大(最小)值, 这里(a,b)也可以是(-∞,+∞).
(1)求函数y=f(x)在x=-2时对应的切线方程;
(2)求函数y=f(x)在[-2,1]上的最大值与最小值.
解 (1)f′(x)=-3x2+2ax+b,
当x=-2时,f(-2)=2,即切点为(-2,2).
又因为切线斜率k=f′(-2)=-8,
所以,所求切线方程为y-2=-8(x+2),即8x+y+14=0.
(2)当x变化时,f′(x),f(x)的变化情况如下表:
(1)当a=-2时,求函数f(x)的极大值;
(2)若函数f(x)有极大值,求实数a的取值范围.
解 (1)因为a=-2,所以f′(x)=1-2sin x.
(2)f′(x)=1+asin x.
①当|a|≤1时,|asin x|<1,
所以f(x)在x=β处取得极大值.
综上所述,实数a的取值范围是(-∞,-1).
要点四 导数与函数、不等式的综合应用
利用导数研究函数是高考的必考内容,也是高考的重点、热点.考题利用导数作为工具,考查求函数的单调区间、函数的极值与最值,参数的取值范围等问题,若以选择题、填空题出现,以中低档题为主;若以解答题形式出现,则难度以中档以上为主,有时也以压轴题的形式出现.考查中常渗透函数、不等式等有关知识,综合性较强.
【例4】 已知函数f(x)=xln x.
(1)求f(x)的最小值;
(2)若对所有x≥1都有f(x)≥ax-1,求实数a的取值范围;
(3)若关于x的方程f(x)=b恰有两个不相等的实数根,求实数b的取值范围.
解 (1)f(x)的定义域是(0,+∞),f′(x)=1+ln x,
(2)∵f(x)=xln x,
当x≥1时,f(x)≥ax-1恒成立,
等价于xln x≥ax-1(x≥1)恒成立,
∴g(x)在[1,+∞)上单调递增,∴g(x)min=g(1)=1,
∴a≤1,即实数a的取值范围为(-∞,1].
(3)若关于x的方程f(x)=b恰有两个不相等的实数根,即y=b的图象和y=f(x)的图象在(0,+∞)上有两个不同的交点,
(1)若对任意实数x,f′(x)≥m恒成立,求m的最大值;
(2)若函数f(x)恰有一个零点,求a的取值范围.
(2)f′(x)=3x2-9x+6=3(x-2)(x-1),
由f′(x)>0 x>2或x<1,由f′(x)<0 1
