北师大版八年级数学下册同步练习第1章三角形的证明复习题(word版 含解析)
文档属性
| 名称 | 北师大版八年级数学下册同步练习第1章三角形的证明复习题(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 652.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 09:02:21 | ||
图片预览



文档简介
北师大版八年级数学下册同步练习 第1章 三角形的证明 复习题
一、单选题
1.在等腰三角形ABC中,∠A=2∠B,则∠C的度数为( )
A.36° B.45° C.36°或45° D.45°或72°
2.有两边相等的三角形的两边长为,,则它的周长为( )
A. B. C. D.或
3.如图,在中,,为的角平分线.若,则点到的距离为( )
A.3 B.4 C.5 D.6
4.如图,O是正内一点,,,.将线段以点B为旋转中心逆时针旋转60°得到线段,下列结论错误的是( )
A.点O与的距离为4 B.
C.S四边形AOBO′ D.
5.如图所示,在Rt△ABC中,∠BAC=90°,AD⊥BC,∠C= 60°,CD=2,则BD=( )
A.2 B.3 C.6 D.8
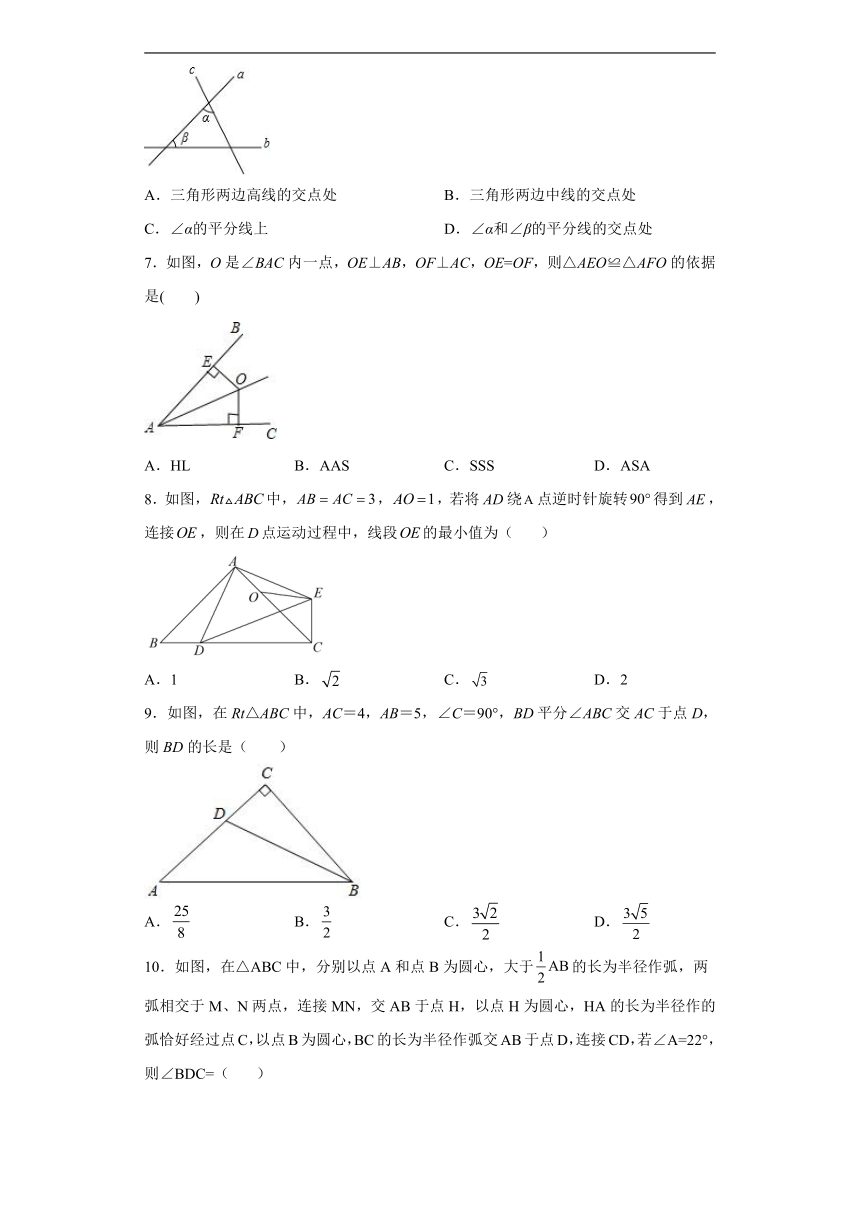
6.如图,a、b、c三条公路的位置相交成三角形,现决定在三条公路之间建一购物超市,使超市到三条公路的距离相等,则超市应建在( )
A.三角形两边高线的交点处 B.三角形两边中线的交点处
C.∠α的平分线上 D.∠α和∠β的平分线的交点处
7.如图,O是∠BAC内一点,OE⊥AB,OF⊥AC,OE=OF,则△AEO≌△AFO的依据是( )
A.HL B.AAS C.SSS D.ASA
8.如图,中,,,若将绕点逆时针旋转得到,连接,则在点运动过程中,线段的最小值为( )
A.1 B. C. D.2
9.如图,在Rt△ABC中,AC=4,AB=5,∠C=90°,BD平分∠ABC交AC于点D,则BD的长是( )
A. B. C. D.
10.如图,在△ABC中,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M、N两点,连接MN,交AB于点H,以点H为圆心,HA的长为半径作的弧恰好经过点C,以点B为圆心,BC的长为半径作弧交AB于点D,连接CD,若∠A=22°,则∠BDC=( )
A.52° B.55° C.56° D.60°
11.下面所给的点在函数的图象上的是( )
A. B. C. D.
12.如图,在给定的正方形中,点从点出发,沿边方向向终点运动, 交于点,以,为邻边构造平行四边形,连接,则的度数的变化情况是( )
A.一直减小 B.一直减小后增大 C.一直不变 D.先增大后减小
二、填空题
13.证明命题“直角三角形中的两个锐角中至少有一个角不小于45°”时,如果用反证法证明,应先假设__________________________________.
14.如图,中,,,平分,交于点.若,则的长为______.
15.如图,点E在正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作EF的垂线,垂足为点H,与BC交于点G.若BG=3,CG=2,则CE的长为________.
16.如图,在中,,的垂直平分线交于点D,且的周长为,则________.
17.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC∶∠EDA=1∶2,且AC=10,则EC的长度是________.
18.在继承和发扬红色学校光荣传统,与时俱进,把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上,如图所示,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离有5米.则旗杆的高度______.
三、解答题
19.已知:如图,D为△ABC外角∠ACP平分线上一点,且DA=DB,DM⊥BP于点M.
(1)若AC=6,DM=2,求△ACD的面积;
(2)求证:AC=BM+CM.
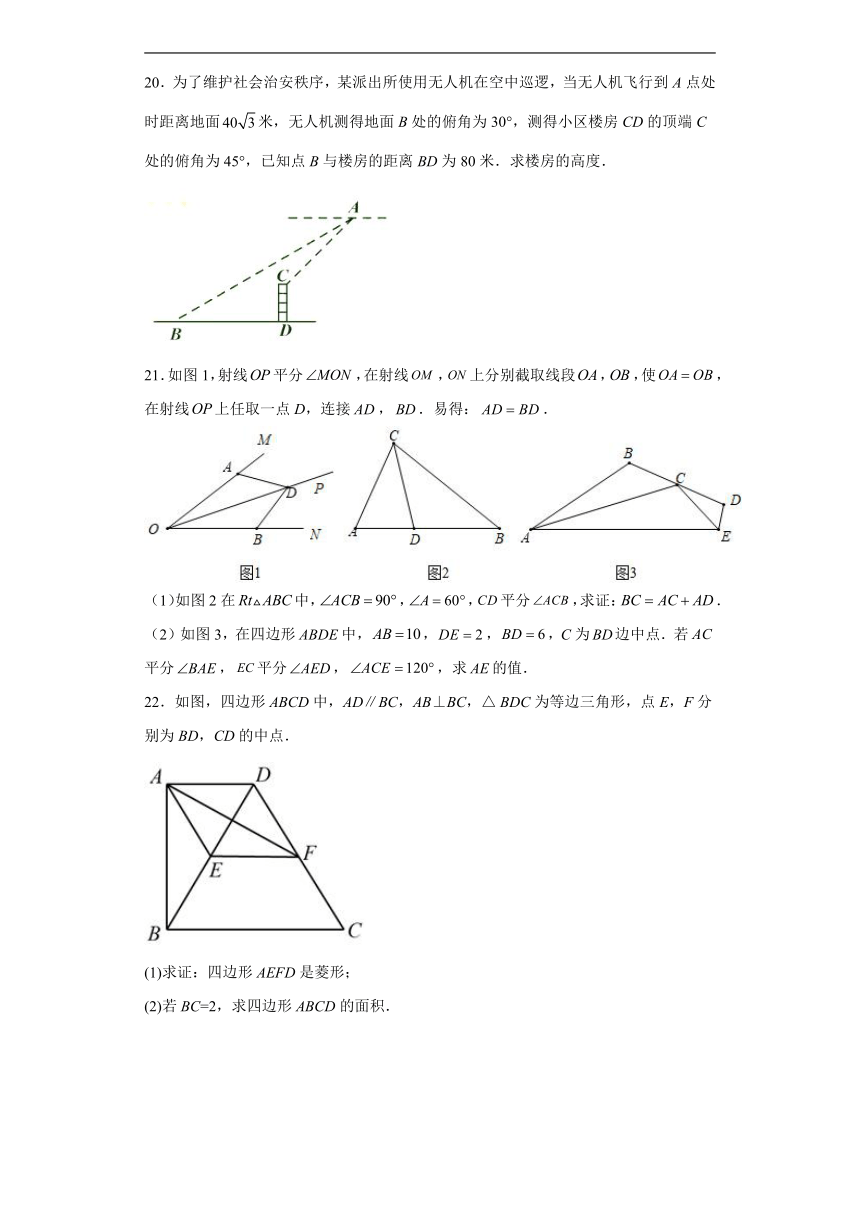
20.为了维护社会治安秩序,某派出所使用无人机在空中巡逻,当无人机飞行到A点处时距离地面米,无人机测得地面B处的俯角为30°,测得小区楼房CD的顶端C处的俯角为45°,已知点B与楼房的距离BD为80米.求楼房的高度.
21.如图1,射线平分,在射线,上分别截取线段,,使,在射线上任取一点D,连接,.易得:.
(1)如图2在中,,,平分,求证:.
(2)如图3,在四边形中,,,,C为边中点.若平分,平分,,求的值.
22.如图,四边形ABCD中,AD∥BC,AB⊥BC,△ BDC为等边三角形,点E,F分别为BD,CD的中点.
(1)求证:四边形AEFD是菱形;
(2)若BC=2,求四边形ABCD的面积.
参考答案:
1.D
【解析】
【分析】
分∠A是顶角和底角两种情况分类讨论列出方程求解即可.
【详解】
解:设∠B=x°,则∠A=2x°,
当∠A是顶角时,∠A+2∠B=180°,
即:4x=180,
解得:x=45,
此时∠C=∠B=45°;
当∠A是底角时,2∠A+∠B=180°,
即5x=180,
解得:x=36°,
此时∠C=∠A=72°,
故选:D.
【点睛】
本题考查了等腰三角形的性质,能够进行分类讨论是解答本题的关键,难度不大.
2.D
【解析】
【分析】
有两边相等的三角形,是等腰三角形,两边分别为和,但没有明确哪是底边,哪是腰,所以有两种情况,需要分类讨论.
【详解】
解:当4为底时,其它两边都为5,
4、5、5可以构成三角形,周长为;
当4为腰时,其它两边为4和5,
4、4、5可以构成三角形,周长为.
综上所述,该等腰三角形的周长是或.
故选:D.
【点睛】
本题考查了等腰三角形的性质和三角形的三边关系,解题的关键是对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.
3.B
【解析】
【分析】
根据题意作出点D到AC的距离ED,再根据角平分线的性质求解即可.
【详解】
解:如图所示,过点D作于点E,则ED的长度为点到的距离.
∵为的角平分线,,,,
∴ED=BD=4.
故选:B.
【点睛】
本题考查了角平分线的性质,熟练掌握角平分线上的点到两边的距离是解题关键.
4.D
【解析】
【分析】
证明,得是等边三角形,根据勾股定理逆定理可得是直角三角形,进而可判断.
【详解】
解:如图1,连接OO′,
由题意可知,∠1+∠2=∠3+∠2=60°,
∴∠1=∠3,
又∵OB=O′B,AB=BC,
∴,
又∵∠OBO′=60°,
∴△OBO′是等边三角形,
∴OO′=OB=4.
故A正确;
∵△BO′A≌△BOC,
∴O′A=5.
在△AOO′中,三边长为3,4,5,这是一组勾股数,
∴△AOO′是直角三角形,∠AOO′=90°,
∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,
故B正确;
S四边形AOBO′=S△AOO′+S△OBO′═×3×4+×42=6+4,
故C正确;
如图2
将绕点顺时针旋转60°到位置,
同理可得,
故D错误;
故选D.
【点睛】
此题考查了旋转的性质,等边三角形、直角三角形的性质,熟练掌握旋转的性质是解本题的关键.
5.C
【解析】
【分析】
依次根据含30°角的直角三角形的特点求得AC和BC,从而可求得BD.
【详解】
解:∵AD⊥BC,∠C= 60°,
∴∠DAC=30°,
∴AC=2CD=2×2=4,
在Rt△ABC中,∠BAC=90°,∠C= 60°,
∴∠A=90°-60°=30°,
∴BC=2AC=2×4=8,
∴BD=BC-DC=8-2=6.
故答案为:C.
【点睛】
本题考查直角三角形两锐角互余,含30°角的直角三角形.理解直角三角形30°角所对边是直角边的一半是解题关键.
6.D
【解析】
【分析】
根据题意知,超市应该是△ABC的内心,即该三角形的内角平分线的交点.
【详解】
∵如图,要建一超市到a、b、c三条公路的距离相等,
∴该超市是△ABC的内心,
∴超市应该建在∠α和∠β的平分线的交点处.
故选:D.
【点睛】
本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.
7.A
【解析】
【分析】
由OE⊥AB,OF⊥AC,可知△AEO和△AFO是直角三角形,利用HL证明△AEO≌△AFO即可得出答案.
【详解】
解:∵OE⊥AB,OF⊥AC,
∴∠AEO=∠AFO=90°,
又∵OE=OF,AO为公共边,
∴△AEO≌△AFO.
故选A.
【点睛】
本题考查学生对直角三角形全等的判定的理解和掌握,解题的关键是利用题目中给出的已知条件判定△AEO和△AFO是直角三角形.
8.B
【解析】
【分析】
在AB上截取AQ=AO=1,利用SAS证明△AQD≌△AOE,推出QD=OE,当QD⊥BC时,QD的值最小,即线段OE有最小值,利用勾股定理即可求解.
【详解】
如图,在AB上截取AQ=AO=1,连接DQ,
∵将AD绕A点逆时针旋转90°得到AE,
∴∠BAC=∠DAE=90°,
∴∠BAC-∠DAC =∠DAE-∠DAC,即∠BAD=∠CAE,
在△AQD和△AOE中,
,
∴△AQD≌△AOE(SAS),
∴QD=OE,
∵D点在线段BC上运动,
∴当QD⊥BC时,QD的值最小,即线段OE 有最小值,
∵△ABC是等腰直角三角形,
∴∠B=45°,
∵QD⊥BC,
∴△QBD是等腰直角三角形,
∵AB=AC=3,AO=1,
∴QB=2,
∴由勾股定理得QD=QB=,
∴线段OE有最小值为,
故选:B.
【点睛】
本题考查了勾股定理,等腰直角三角形的判定和性质,全等三角形的判定和性质,旋转的性质,熟记各图形的性质并准确识图是解题的关键.
9.D
【解析】
【分析】
根据勾股定理得到BC=3,过D作DE⊥AB于E,根据角平分线的性质得到CD=DE,根据全等三角形的性质得到BE=BC=3,根据勾股定理即可得到结论.
【详解】
解:在Rt△ABC中,AC=4,AB=5,∠C=90°,
∴,
过D作DE⊥AB于E,
∵BD平分∠ABC,∠C=90°,
∴CD=DE,
在Rt△BCD与Rt△BED中,
,
∴Rt△BCD≌Rt△BED(HL),
∴BE=BC=3,
∴AE=2,
∵AD2=DE2+AE2,
∴,
∴,
∴.
故选:D.
【点睛】
此题主要考查了勾股定理,全等三角形的判定与性质,角平分线的性质,解题的关键是灵活利用相关性质进行求解.
10.C
【解析】
【分析】
根据做法可知:MN是AB的垂直平分线,AH=BH=CH,得出∠ACB=,又根据做法可知:BC=BD,即可求解.
【详解】
解:∵根据做法可知:MN是AB的垂直平分线
∴AH=BH=CH
∴∠ACB=
∵∠A=22°
∴∠B=
∵又根据做法可知:BC=BD
∴∠BDC=
故选:C
【点睛】
此题主要考查尺规作图,根据尺规作图的信息,利用特殊三角形的内角和是解题关键.
11.B
【解析】
【分析】
直接把各点代入函数y=-2x进行检验即可.
【详解】
A、∵当x=2时,y=-4≠-1,∴此点不在函数图象上,故本选项错误;
B、∵当x=-1时,y=2,∴此点在函数图象上,故本选项正确;
C、∵当x=1时,y=-2≠2,∴此点不在函数图象上,故本选项错误;
D、∵当x=2时,y=-4≠1,∴此点不在函数图象上,故本选项错误.
故选B.
【点睛】
本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
12.A
【解析】
【分析】
根据题意,作交的延长线于,证明是的角平分线即可解决问题.
【详解】
解:作交的延长线于,
∵四边形 是正方形,
∴,
,
∵,
∴,,
∴,
∴,
∴,
∵四边形是平行四边形,
∴,,
∵, ,
∴,
∵,.
∴,
∴,,
∴,
∴,
∵,
∴,
∴是的角平分线,
∴点的运动轨迹是的角平分线,
∵,
由图可知,点P从点D开始运动,所以一直减小,
故选:A .
【点睛】
本题考查了正方形的性质、全等三角形的判定和性质、平行四边形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
13.两个锐角都小于45°
【解析】
【分析】
根据命题“直角三角形中的两个锐角中至少有一个角不小于45°”的否定是:两个锐角都小于45°,即可得到答案.
【详解】
用反证法证明命题“直角三角形中的两个锐角中至少有一个角不小于45°”时,应该假设每一个锐角都小于45°,即两个锐角都小于45°.
故答案是:两个锐角都小于45°.
【点睛】
本题主要考查命题证明的反证法,掌握反证法的第一步是假设命题的结论不成立,是解题的关键.
14.2
【解析】
【分析】
先计算出得到,则,再利用含30度的直角三角形的性质得到,则.
【详解】
解:,,
,
平分,
,
,
,
∵,,,
∴,
,
故答案为:2.
【点睛】
本题考查了角平分线的定义,等腰三角形的判定以及含30度的直角三角形的性质,熟练掌握相关图形的性质是解决本题的关键.
15.
【解析】
【详解】
解:如图所示,连接EG,
由旋转可知△ABF≌△ADE,
∴DE=BF,AE=AF,
∵AG⊥EF,
∴H为EF的中点,
∴AG垂直平分EF,
∴EG=FG,
设CE=x,则DE=5-x=BF,FG=EG=BF+BG=8-x,
∵∠C=90°,
∴CE2+CG2=EG2
即x2+22=(8 x)2
解得x=,
∴CE的长为,
故答案为:.
【点睛】
本题主要考查了正方形的性质以及旋转的性质,解决该题的关键是根据勾股定理列方程.
16.7
【解析】
【分析】
根据是的垂直平分线可得,结合的周长为可得结论.
【详解】
∵是的垂直平分线,
∴,
∵的周长为,
∴,
又∵,
∴.
故答案为:7.
【点睛】
本题考查了垂直平分线的性质,熟知垂直平分线上的任意一点到两端点的距离相等是解题的关键.
17.2.5##
【解析】
【分析】
根据∠EDC:∠EDA=1: 2,可得∠EDC=30°, ∠EDA=60°,进而得出DC=AC,进而求得CE的长.
【详解】
解:∵四边形ABCD是矩形,
∴∠ADC = 90°, AC= BD= 10,OA= OC=AC = 5,ОВ=OD=BD=5,
∴OС = OD,
∴∠ODC = ∠OCD ,
∵∠EDC:∠EDA=1:2,∠EDC+∠EDA=90°,
∴∠EDC = 30°,∠EDA= 60°,
∵DE⊥ AC,
∴∠DEC= 90°,
∴∠DAC= 30°,
∴DC=AC= 5,
∴EC =DC= 2.5.
故答案为:2.5.
【点睛】
本题主要考查了直角三角形的性质和矩形的性质,根据已知得出∠DAC=30°是解题关键.
18.12米
【解析】
【分析】
设旗杆的高度是x米,绳子长为(x+1)米,旗杆,拉直的绳子和BC构成直角三角形,根据勾股定理可求出x的值,从而求出旗杆的高度.
【详解】
解:设旗杆的高度为米,根据题意可得:
,
解得:,
答:旗杆的高度为12米.
故答案为:12米.
【点睛】
本题考查勾股定理的应用,关键看到旗杆,拉直的绳子和BC构成直角三角形,根据勾股定理可求解.
19.(1)6;(2)见解析
【解析】
【分析】
(1)如图作DN⊥AC于N.根据角平分线的性质定理可得DM=DN=2,由此即可解决问题;
(2)由Rt△CDM≌Rt△CDN,推出CN=CM,由Rt△ADN≌Rt△BDM,推出AN=BM,由此即可解决问题.
【详解】
(1)解:如图作DN⊥AC于N.
∵DC平分∠ACP,DM⊥CP,DN⊥CA,
∴DM=DN=2,
∴S△ADC= AC DN=×6×2=6.
(2)∵CD=CD,DM=DN,
∴Rt△CDM≌Rt△CDN,
∴CN=CM,
∵AD=BD,DN=DM,
∴Rt△ADN≌Rt△BDM,
∴AN=BM,
∴AC=AN+CN=BM+CM.
【点睛】
本题考查全等三角形的判定和性质、角平分线的性质定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
20.楼房的高度为米
【解析】
【分析】
过点A作,垂足为点E,过点C作,垂足为点F,根据等腰直角三角形及矩形的性质可得,再根据即可解答.
【详解】
如图过点A作,垂足为点E,过点C作,垂足为点F
由题可知:,
∵,
∴,
∵、、
∴四边形CDEF为矩形
设米,则米,
∵米,米,
在中,
∴解得,
∴米
∴楼房的高度为米.
【点睛】
本题考查了等腰直角三角形及矩形的判定与性质、特殊角的三角函数等知识点,正确作出辅助线并熟练掌握上述知识点是解答本题的关键.
21.(1)见解析;(2)15
【解析】
【分析】
(1)在BC上截取CE=CA,连接DE,由题意易得∠ACD=∠ECD,∠B=30°,则有△ACD≌△ECD,然后可得∠A=∠CED=60°,则根据三角形外角的性质可得∠EDB=∠B=30°,然后可得DE=BE,进而问题可求证;
(2)在AE上分别截取AF=AB,EG=ED,连接CF、CG,同理(1)可证△ABC≌△AFC,△CDE≌△CGE,则有∠ACB=∠ACF,∠DCE=∠GCE,然后可得∠ACF+∠GCE=60°,进而可得△CFG是等边三角形,最后问题可求解.
【详解】
(1)在BC上截取CE=CA,连接DE,如图所示:
∵∠ACB=90°,∠A=60°,CD平分∠ACB,
∴∠ACD=∠ECD,∠B=30°,
∵CD=CD,
∴△ACD≌△ECD(SAS),
∴∠A=∠CED=60°,AD=DE,
∵∠B+∠EDB=∠CED,
∴∠EDB=∠B=30°,
∴DE=BE,
∴AD=BE,
∵BC=CE+BE,
∴BC=AC+AD.
(2)在AE上分别截取AF=AB=10,EG=ED=2,连接CF、CG,如图所示:
同理(1)可得:△ABC≌△AFC,△CDE≌△CGE,
∴∠ACB=∠ACF,∠DCE=∠GCE,BC=CF,CD=CG,DE=GE=2,
∵C为BD边中点,
∴BC=CD=CF=CG=3,
∵∠ACE=120°,
∴∠ACB+∠DCE=60°,
∴∠ACF+∠GCE=60°,
∴∠FCG=60°,
∴△CFG是等边三角形,
∴FG=CF=CG=3,
∴AE=AF+FG+GE=10+3+2=15.
【点睛】
本题主要考查三角形全等的性质与判定、角平分线的定义、等腰三角形的性质与判定及等边三角形的性质与判定,解题的关键是构造辅助线证明三角形全等.
22.(1)见解析
(2)
【解析】
【分析】
(1)证明△DEF和△ADE是等边三角形,进而得到AE=AD=DE=DF=EF,再由四边均相等的四边形是菱形即可证明;
(2)由BC=2求出AD=EF=1,再在Rt△ABD中由∠ABD=30°求出AB,最后根据梯形的面积公式即可求出梯形ABCD的面积.
(1)
证明:∵△ BDC为等边三角形,
∴DB=DC,∠BDC=60°,∠DBC=60°
∵点E,F分别为BD,CD的中点.
∴DE=DB=DC=DF,
∴△DEF为等边三角形,
∴DE=DF=EF,
∵∠ABD=∠ABC-∠DBC=90°-60°=30°,且E为BD的中点,
∴AE=DB=ED,
且∠ADE=180°-∠BAD-∠ABD=180°-90°-30°=60°,
∴△ADE为等边三角形,
∴AD=AE=DE=DF=EF,
∴四边形AEFD是菱形
(2)
解:∵点E,F分别为BD,CD的中点.
∴AD=EF=BC=1,BD=BC=2,
∵∠ABD=30°,∠BAD=90°,
∴△ABD三边之比为,
∴AB=AD=,
∴,
∴四边形ABCD的面积为.
【点睛】
本题考查了菱形的判定定理、三角形的中位线定理、等边三角形的判定等,熟练掌握各图形的性质是解决本类题的关键.
一、单选题
1.在等腰三角形ABC中,∠A=2∠B,则∠C的度数为( )
A.36° B.45° C.36°或45° D.45°或72°
2.有两边相等的三角形的两边长为,,则它的周长为( )
A. B. C. D.或
3.如图,在中,,为的角平分线.若,则点到的距离为( )
A.3 B.4 C.5 D.6
4.如图,O是正内一点,,,.将线段以点B为旋转中心逆时针旋转60°得到线段,下列结论错误的是( )
A.点O与的距离为4 B.
C.S四边形AOBO′ D.
5.如图所示,在Rt△ABC中,∠BAC=90°,AD⊥BC,∠C= 60°,CD=2,则BD=( )
A.2 B.3 C.6 D.8
6.如图,a、b、c三条公路的位置相交成三角形,现决定在三条公路之间建一购物超市,使超市到三条公路的距离相等,则超市应建在( )
A.三角形两边高线的交点处 B.三角形两边中线的交点处
C.∠α的平分线上 D.∠α和∠β的平分线的交点处
7.如图,O是∠BAC内一点,OE⊥AB,OF⊥AC,OE=OF,则△AEO≌△AFO的依据是( )
A.HL B.AAS C.SSS D.ASA
8.如图,中,,,若将绕点逆时针旋转得到,连接,则在点运动过程中,线段的最小值为( )
A.1 B. C. D.2
9.如图,在Rt△ABC中,AC=4,AB=5,∠C=90°,BD平分∠ABC交AC于点D,则BD的长是( )
A. B. C. D.
10.如图,在△ABC中,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M、N两点,连接MN,交AB于点H,以点H为圆心,HA的长为半径作的弧恰好经过点C,以点B为圆心,BC的长为半径作弧交AB于点D,连接CD,若∠A=22°,则∠BDC=( )
A.52° B.55° C.56° D.60°
11.下面所给的点在函数的图象上的是( )
A. B. C. D.
12.如图,在给定的正方形中,点从点出发,沿边方向向终点运动, 交于点,以,为邻边构造平行四边形,连接,则的度数的变化情况是( )
A.一直减小 B.一直减小后增大 C.一直不变 D.先增大后减小
二、填空题
13.证明命题“直角三角形中的两个锐角中至少有一个角不小于45°”时,如果用反证法证明,应先假设__________________________________.
14.如图,中,,,平分,交于点.若,则的长为______.
15.如图,点E在正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作EF的垂线,垂足为点H,与BC交于点G.若BG=3,CG=2,则CE的长为________.
16.如图,在中,,的垂直平分线交于点D,且的周长为,则________.
17.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC∶∠EDA=1∶2,且AC=10,则EC的长度是________.
18.在继承和发扬红色学校光荣传统,与时俱进,把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上,如图所示,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离有5米.则旗杆的高度______.
三、解答题
19.已知:如图,D为△ABC外角∠ACP平分线上一点,且DA=DB,DM⊥BP于点M.
(1)若AC=6,DM=2,求△ACD的面积;
(2)求证:AC=BM+CM.
20.为了维护社会治安秩序,某派出所使用无人机在空中巡逻,当无人机飞行到A点处时距离地面米,无人机测得地面B处的俯角为30°,测得小区楼房CD的顶端C处的俯角为45°,已知点B与楼房的距离BD为80米.求楼房的高度.
21.如图1,射线平分,在射线,上分别截取线段,,使,在射线上任取一点D,连接,.易得:.
(1)如图2在中,,,平分,求证:.
(2)如图3,在四边形中,,,,C为边中点.若平分,平分,,求的值.
22.如图,四边形ABCD中,AD∥BC,AB⊥BC,△ BDC为等边三角形,点E,F分别为BD,CD的中点.
(1)求证:四边形AEFD是菱形;
(2)若BC=2,求四边形ABCD的面积.
参考答案:
1.D
【解析】
【分析】
分∠A是顶角和底角两种情况分类讨论列出方程求解即可.
【详解】
解:设∠B=x°,则∠A=2x°,
当∠A是顶角时,∠A+2∠B=180°,
即:4x=180,
解得:x=45,
此时∠C=∠B=45°;
当∠A是底角时,2∠A+∠B=180°,
即5x=180,
解得:x=36°,
此时∠C=∠A=72°,
故选:D.
【点睛】
本题考查了等腰三角形的性质,能够进行分类讨论是解答本题的关键,难度不大.
2.D
【解析】
【分析】
有两边相等的三角形,是等腰三角形,两边分别为和,但没有明确哪是底边,哪是腰,所以有两种情况,需要分类讨论.
【详解】
解:当4为底时,其它两边都为5,
4、5、5可以构成三角形,周长为;
当4为腰时,其它两边为4和5,
4、4、5可以构成三角形,周长为.
综上所述,该等腰三角形的周长是或.
故选:D.
【点睛】
本题考查了等腰三角形的性质和三角形的三边关系,解题的关键是对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.
3.B
【解析】
【分析】
根据题意作出点D到AC的距离ED,再根据角平分线的性质求解即可.
【详解】
解:如图所示,过点D作于点E,则ED的长度为点到的距离.
∵为的角平分线,,,,
∴ED=BD=4.
故选:B.
【点睛】
本题考查了角平分线的性质,熟练掌握角平分线上的点到两边的距离是解题关键.
4.D
【解析】
【分析】
证明,得是等边三角形,根据勾股定理逆定理可得是直角三角形,进而可判断.
【详解】
解:如图1,连接OO′,
由题意可知,∠1+∠2=∠3+∠2=60°,
∴∠1=∠3,
又∵OB=O′B,AB=BC,
∴,
又∵∠OBO′=60°,
∴△OBO′是等边三角形,
∴OO′=OB=4.
故A正确;
∵△BO′A≌△BOC,
∴O′A=5.
在△AOO′中,三边长为3,4,5,这是一组勾股数,
∴△AOO′是直角三角形,∠AOO′=90°,
∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,
故B正确;
S四边形AOBO′=S△AOO′+S△OBO′═×3×4+×42=6+4,
故C正确;
如图2
将绕点顺时针旋转60°到位置,
同理可得,
故D错误;
故选D.
【点睛】
此题考查了旋转的性质,等边三角形、直角三角形的性质,熟练掌握旋转的性质是解本题的关键.
5.C
【解析】
【分析】
依次根据含30°角的直角三角形的特点求得AC和BC,从而可求得BD.
【详解】
解:∵AD⊥BC,∠C= 60°,
∴∠DAC=30°,
∴AC=2CD=2×2=4,
在Rt△ABC中,∠BAC=90°,∠C= 60°,
∴∠A=90°-60°=30°,
∴BC=2AC=2×4=8,
∴BD=BC-DC=8-2=6.
故答案为:C.
【点睛】
本题考查直角三角形两锐角互余,含30°角的直角三角形.理解直角三角形30°角所对边是直角边的一半是解题关键.
6.D
【解析】
【分析】
根据题意知,超市应该是△ABC的内心,即该三角形的内角平分线的交点.
【详解】
∵如图,要建一超市到a、b、c三条公路的距离相等,
∴该超市是△ABC的内心,
∴超市应该建在∠α和∠β的平分线的交点处.
故选:D.
【点睛】
本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.
7.A
【解析】
【分析】
由OE⊥AB,OF⊥AC,可知△AEO和△AFO是直角三角形,利用HL证明△AEO≌△AFO即可得出答案.
【详解】
解:∵OE⊥AB,OF⊥AC,
∴∠AEO=∠AFO=90°,
又∵OE=OF,AO为公共边,
∴△AEO≌△AFO.
故选A.
【点睛】
本题考查学生对直角三角形全等的判定的理解和掌握,解题的关键是利用题目中给出的已知条件判定△AEO和△AFO是直角三角形.
8.B
【解析】
【分析】
在AB上截取AQ=AO=1,利用SAS证明△AQD≌△AOE,推出QD=OE,当QD⊥BC时,QD的值最小,即线段OE有最小值,利用勾股定理即可求解.
【详解】
如图,在AB上截取AQ=AO=1,连接DQ,
∵将AD绕A点逆时针旋转90°得到AE,
∴∠BAC=∠DAE=90°,
∴∠BAC-∠DAC =∠DAE-∠DAC,即∠BAD=∠CAE,
在△AQD和△AOE中,
,
∴△AQD≌△AOE(SAS),
∴QD=OE,
∵D点在线段BC上运动,
∴当QD⊥BC时,QD的值最小,即线段OE 有最小值,
∵△ABC是等腰直角三角形,
∴∠B=45°,
∵QD⊥BC,
∴△QBD是等腰直角三角形,
∵AB=AC=3,AO=1,
∴QB=2,
∴由勾股定理得QD=QB=,
∴线段OE有最小值为,
故选:B.
【点睛】
本题考查了勾股定理,等腰直角三角形的判定和性质,全等三角形的判定和性质,旋转的性质,熟记各图形的性质并准确识图是解题的关键.
9.D
【解析】
【分析】
根据勾股定理得到BC=3,过D作DE⊥AB于E,根据角平分线的性质得到CD=DE,根据全等三角形的性质得到BE=BC=3,根据勾股定理即可得到结论.
【详解】
解:在Rt△ABC中,AC=4,AB=5,∠C=90°,
∴,
过D作DE⊥AB于E,
∵BD平分∠ABC,∠C=90°,
∴CD=DE,
在Rt△BCD与Rt△BED中,
,
∴Rt△BCD≌Rt△BED(HL),
∴BE=BC=3,
∴AE=2,
∵AD2=DE2+AE2,
∴,
∴,
∴.
故选:D.
【点睛】
此题主要考查了勾股定理,全等三角形的判定与性质,角平分线的性质,解题的关键是灵活利用相关性质进行求解.
10.C
【解析】
【分析】
根据做法可知:MN是AB的垂直平分线,AH=BH=CH,得出∠ACB=,又根据做法可知:BC=BD,即可求解.
【详解】
解:∵根据做法可知:MN是AB的垂直平分线
∴AH=BH=CH
∴∠ACB=
∵∠A=22°
∴∠B=
∵又根据做法可知:BC=BD
∴∠BDC=
故选:C
【点睛】
此题主要考查尺规作图,根据尺规作图的信息,利用特殊三角形的内角和是解题关键.
11.B
【解析】
【分析】
直接把各点代入函数y=-2x进行检验即可.
【详解】
A、∵当x=2时,y=-4≠-1,∴此点不在函数图象上,故本选项错误;
B、∵当x=-1时,y=2,∴此点在函数图象上,故本选项正确;
C、∵当x=1时,y=-2≠2,∴此点不在函数图象上,故本选项错误;
D、∵当x=2时,y=-4≠1,∴此点不在函数图象上,故本选项错误.
故选B.
【点睛】
本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
12.A
【解析】
【分析】
根据题意,作交的延长线于,证明是的角平分线即可解决问题.
【详解】
解:作交的延长线于,
∵四边形 是正方形,
∴,
,
∵,
∴,,
∴,
∴,
∴,
∵四边形是平行四边形,
∴,,
∵, ,
∴,
∵,.
∴,
∴,,
∴,
∴,
∵,
∴,
∴是的角平分线,
∴点的运动轨迹是的角平分线,
∵,
由图可知,点P从点D开始运动,所以一直减小,
故选:A .
【点睛】
本题考查了正方形的性质、全等三角形的判定和性质、平行四边形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
13.两个锐角都小于45°
【解析】
【分析】
根据命题“直角三角形中的两个锐角中至少有一个角不小于45°”的否定是:两个锐角都小于45°,即可得到答案.
【详解】
用反证法证明命题“直角三角形中的两个锐角中至少有一个角不小于45°”时,应该假设每一个锐角都小于45°,即两个锐角都小于45°.
故答案是:两个锐角都小于45°.
【点睛】
本题主要考查命题证明的反证法,掌握反证法的第一步是假设命题的结论不成立,是解题的关键.
14.2
【解析】
【分析】
先计算出得到,则,再利用含30度的直角三角形的性质得到,则.
【详解】
解:,,
,
平分,
,
,
,
∵,,,
∴,
,
故答案为:2.
【点睛】
本题考查了角平分线的定义,等腰三角形的判定以及含30度的直角三角形的性质,熟练掌握相关图形的性质是解决本题的关键.
15.
【解析】
【详解】
解:如图所示,连接EG,
由旋转可知△ABF≌△ADE,
∴DE=BF,AE=AF,
∵AG⊥EF,
∴H为EF的中点,
∴AG垂直平分EF,
∴EG=FG,
设CE=x,则DE=5-x=BF,FG=EG=BF+BG=8-x,
∵∠C=90°,
∴CE2+CG2=EG2
即x2+22=(8 x)2
解得x=,
∴CE的长为,
故答案为:.
【点睛】
本题主要考查了正方形的性质以及旋转的性质,解决该题的关键是根据勾股定理列方程.
16.7
【解析】
【分析】
根据是的垂直平分线可得,结合的周长为可得结论.
【详解】
∵是的垂直平分线,
∴,
∵的周长为,
∴,
又∵,
∴.
故答案为:7.
【点睛】
本题考查了垂直平分线的性质,熟知垂直平分线上的任意一点到两端点的距离相等是解题的关键.
17.2.5##
【解析】
【分析】
根据∠EDC:∠EDA=1: 2,可得∠EDC=30°, ∠EDA=60°,进而得出DC=AC,进而求得CE的长.
【详解】
解:∵四边形ABCD是矩形,
∴∠ADC = 90°, AC= BD= 10,OA= OC=AC = 5,ОВ=OD=BD=5,
∴OС = OD,
∴∠ODC = ∠OCD ,
∵∠EDC:∠EDA=1:2,∠EDC+∠EDA=90°,
∴∠EDC = 30°,∠EDA= 60°,
∵DE⊥ AC,
∴∠DEC= 90°,
∴∠DAC= 30°,
∴DC=AC= 5,
∴EC =DC= 2.5.
故答案为:2.5.
【点睛】
本题主要考查了直角三角形的性质和矩形的性质,根据已知得出∠DAC=30°是解题关键.
18.12米
【解析】
【分析】
设旗杆的高度是x米,绳子长为(x+1)米,旗杆,拉直的绳子和BC构成直角三角形,根据勾股定理可求出x的值,从而求出旗杆的高度.
【详解】
解:设旗杆的高度为米,根据题意可得:
,
解得:,
答:旗杆的高度为12米.
故答案为:12米.
【点睛】
本题考查勾股定理的应用,关键看到旗杆,拉直的绳子和BC构成直角三角形,根据勾股定理可求解.
19.(1)6;(2)见解析
【解析】
【分析】
(1)如图作DN⊥AC于N.根据角平分线的性质定理可得DM=DN=2,由此即可解决问题;
(2)由Rt△CDM≌Rt△CDN,推出CN=CM,由Rt△ADN≌Rt△BDM,推出AN=BM,由此即可解决问题.
【详解】
(1)解:如图作DN⊥AC于N.
∵DC平分∠ACP,DM⊥CP,DN⊥CA,
∴DM=DN=2,
∴S△ADC= AC DN=×6×2=6.
(2)∵CD=CD,DM=DN,
∴Rt△CDM≌Rt△CDN,
∴CN=CM,
∵AD=BD,DN=DM,
∴Rt△ADN≌Rt△BDM,
∴AN=BM,
∴AC=AN+CN=BM+CM.
【点睛】
本题考查全等三角形的判定和性质、角平分线的性质定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
20.楼房的高度为米
【解析】
【分析】
过点A作,垂足为点E,过点C作,垂足为点F,根据等腰直角三角形及矩形的性质可得,再根据即可解答.
【详解】
如图过点A作,垂足为点E,过点C作,垂足为点F
由题可知:,
∵,
∴,
∵、、
∴四边形CDEF为矩形
设米,则米,
∵米,米,
在中,
∴解得,
∴米
∴楼房的高度为米.
【点睛】
本题考查了等腰直角三角形及矩形的判定与性质、特殊角的三角函数等知识点,正确作出辅助线并熟练掌握上述知识点是解答本题的关键.
21.(1)见解析;(2)15
【解析】
【分析】
(1)在BC上截取CE=CA,连接DE,由题意易得∠ACD=∠ECD,∠B=30°,则有△ACD≌△ECD,然后可得∠A=∠CED=60°,则根据三角形外角的性质可得∠EDB=∠B=30°,然后可得DE=BE,进而问题可求证;
(2)在AE上分别截取AF=AB,EG=ED,连接CF、CG,同理(1)可证△ABC≌△AFC,△CDE≌△CGE,则有∠ACB=∠ACF,∠DCE=∠GCE,然后可得∠ACF+∠GCE=60°,进而可得△CFG是等边三角形,最后问题可求解.
【详解】
(1)在BC上截取CE=CA,连接DE,如图所示:
∵∠ACB=90°,∠A=60°,CD平分∠ACB,
∴∠ACD=∠ECD,∠B=30°,
∵CD=CD,
∴△ACD≌△ECD(SAS),
∴∠A=∠CED=60°,AD=DE,
∵∠B+∠EDB=∠CED,
∴∠EDB=∠B=30°,
∴DE=BE,
∴AD=BE,
∵BC=CE+BE,
∴BC=AC+AD.
(2)在AE上分别截取AF=AB=10,EG=ED=2,连接CF、CG,如图所示:
同理(1)可得:△ABC≌△AFC,△CDE≌△CGE,
∴∠ACB=∠ACF,∠DCE=∠GCE,BC=CF,CD=CG,DE=GE=2,
∵C为BD边中点,
∴BC=CD=CF=CG=3,
∵∠ACE=120°,
∴∠ACB+∠DCE=60°,
∴∠ACF+∠GCE=60°,
∴∠FCG=60°,
∴△CFG是等边三角形,
∴FG=CF=CG=3,
∴AE=AF+FG+GE=10+3+2=15.
【点睛】
本题主要考查三角形全等的性质与判定、角平分线的定义、等腰三角形的性质与判定及等边三角形的性质与判定,解题的关键是构造辅助线证明三角形全等.
22.(1)见解析
(2)
【解析】
【分析】
(1)证明△DEF和△ADE是等边三角形,进而得到AE=AD=DE=DF=EF,再由四边均相等的四边形是菱形即可证明;
(2)由BC=2求出AD=EF=1,再在Rt△ABD中由∠ABD=30°求出AB,最后根据梯形的面积公式即可求出梯形ABCD的面积.
(1)
证明:∵△ BDC为等边三角形,
∴DB=DC,∠BDC=60°,∠DBC=60°
∵点E,F分别为BD,CD的中点.
∴DE=DB=DC=DF,
∴△DEF为等边三角形,
∴DE=DF=EF,
∵∠ABD=∠ABC-∠DBC=90°-60°=30°,且E为BD的中点,
∴AE=DB=ED,
且∠ADE=180°-∠BAD-∠ABD=180°-90°-30°=60°,
∴△ADE为等边三角形,
∴AD=AE=DE=DF=EF,
∴四边形AEFD是菱形
(2)
解:∵点E,F分别为BD,CD的中点.
∴AD=EF=BC=1,BD=BC=2,
∵∠ABD=30°,∠BAD=90°,
∴△ABD三边之比为,
∴AB=AD=,
∴,
∴四边形ABCD的面积为.
【点睛】
本题考查了菱形的判定定理、三角形的中位线定理、等边三角形的判定等,熟练掌握各图形的性质是解决本类题的关键.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
