北师大版八年级数学下册同步练习第3章 图形的平移与旋转复习题(word版 含解析)
文档属性
| 名称 | 北师大版八年级数学下册同步练习第3章 图形的平移与旋转复习题(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 816.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 09:06:37 | ||
图片预览



文档简介
北师大版八年级数学下册同步练习 第3章 图形的平移与旋转 复习题
一、单选题
1.下列运动是属于旋转的是( )
A.滚动过程中的篮球的滚动; B.钟表的钟摆的摆动;
C.气球升空的运动; D.一个图形沿某直线对折过程
2.2019年10月18日,第七届军人运动会在武汉举行,如图是第七届运动会的吉祥物兵兵,下列图案中,是通过平移得到的图案是( )
A. B. C. D.
3.下列四个生活安全警示图标,其中是中心对称图形的是( )
A. B. C. D.
4.是由平移得到的,点的对应点为,点的对应点为,则点的对应点的坐标为( )
A. B. C. D.
5.将如图的七巧板的其中几块,拼成一个多边形,为轴对称图形的是( )
A. B.
C. D.
6.如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是( )
A.逆时针旋转90° B.顺时针旋转90° C.逆时针旋转45° D.顺时针旋转45°
7.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
8.已知点与点关于原点对称,则点的坐标( )
A. B. C. D.
9.如图,将△ABC绕点A旋转后得到△ADE,则下列结论不正确的是( )
A.BC=DE B.∠E=∠C C.∠EAC=∠BAD D.∠B=∠E
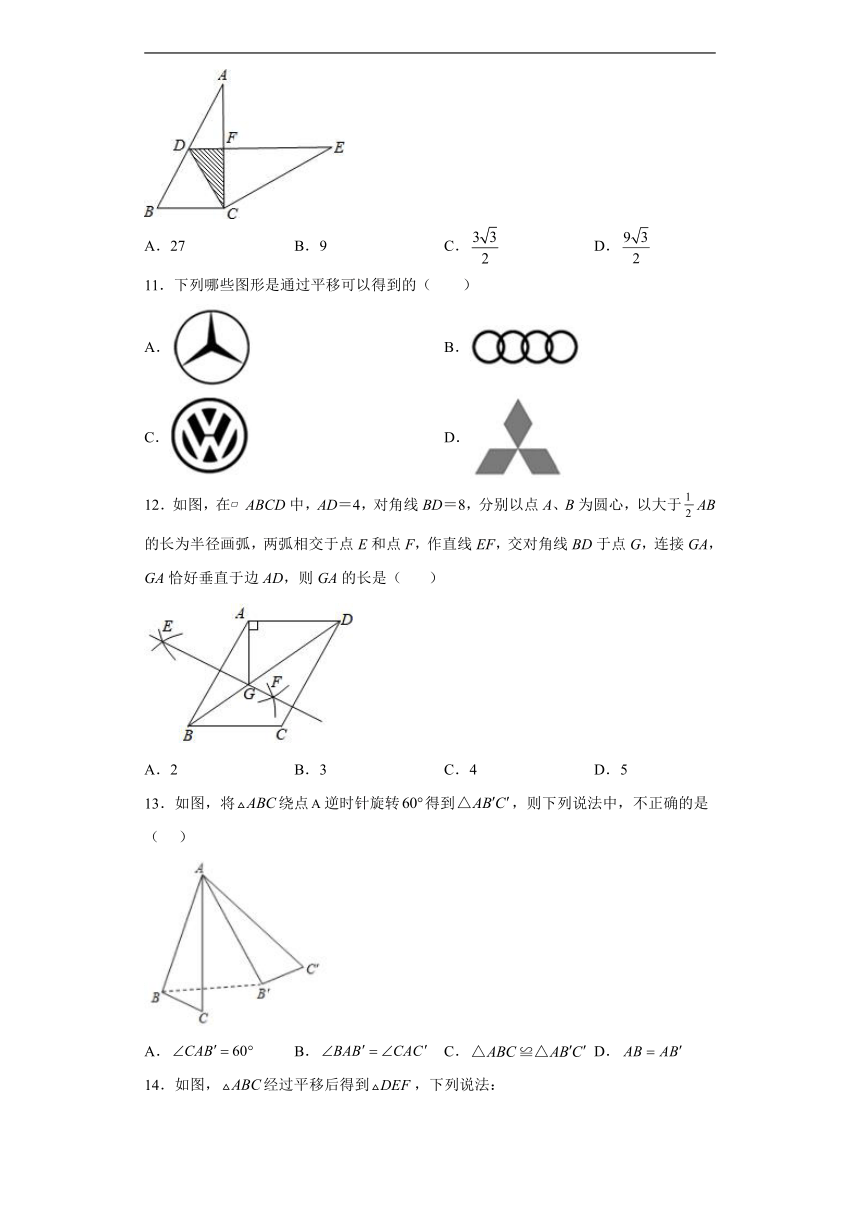
10.如图,在中,.将绕点按顺时针方向旋转 度后得到,此时点在边上,斜边交边于点,则图中阴影部分的面积为( )
A.27 B.9 C. D.
11.下列哪些图形是通过平移可以得到的( )
A. B.
C. D.
12.如图,在 ABCD中,AD=4,对角线BD=8,分别以点A、B为圆心,以大于AB的长为半径画弧,两弧相交于点E和点F,作直线EF,交对角线BD于点G,连接GA,GA恰好垂直于边AD,则GA的长是( )
A.2 B.3 C.4 D.5
13.如图,将绕点逆时针旋转得到,则下列说法中,不正确的是( )
A. B. C. D.
14.如图,经过平移后得到,下列说法:
①
②
③
④和的面积相等
⑤四边形和四边形的面积相等,其中正确的有( )
A.个 B.个 C.个 D.个
15.把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,DC=14,把三角板DCE绕点C顺时针旋转15°得到D1CE1(如图乙),此时AB与 CD1交于点O,则线段AD1的长为( )
A.6 B.10 C.8 D.
二、填空题
16.把点向下平移4个单位长度,可以得到对应点______,再向左平移6个单位长度可以得到对应点_______,则点与点A关于________对称,点与点A关于_________对称,点与点关于_______对称.
17.如图所示,△ABC与△A′B′C′是全等三角形,那么△A′B′C′可以看作是由△ABC以O为旋转中心,旋转_______度形成的.
18.如图:点A表示的数为__.
19.如图,已知,且∠1=48°,则∠2=_____,∠3=_____,∠4=_____.
20.旋转作图的基本步骤:
(1)确定___________、_____________和____________;
(2)找出图形的关键点,一般是图形中的转折点,例如,多边形的关键点 是它的顶点.
(3)作旋转后的对应点,方法如下:
①连:连接图形的每个关键点与__________;
②转:把连线绕旋转中心按旋转方向旋转相同的角度(作旋转角);
③截:在作得的角的另一边截取与关键点到旋转中心的距离相等的线段,得到各个关键点的对应点;
(4)按原图形的顺序连接这些对应点,所得到的图形就是___________.
(5)写出结论,说明作出的图形即为所求的图形.
三、解答题
21.如图,已知和点请画出绕点顺时针旋转后得到的
22.已知四边形四条边相等,它的两个顶点坐标分别为,对角线的交点为.将四边形平移后,顶点A的对应点是,请写出点B,C,D,M对应点的坐标.
23.如图,经过平移,的顶点A移到了点D.
(1)指出平移的方向和平移的距离;
(2)画出平移后的三角形.
24.(1)在平面直角坐标系中描出点,然后用线段依次连接A,B,C,D,E,F,A各点;
(2)将(1)中所画图形先向左平移12个单位长度,再向上平移5个单位长度,画出第二次平移后的图形;
(3)如何将(1)中所画图形经过一次平移得到(2)中所画图形?平移前后对应点的横坐标有什么关系?纵坐标呢?
25.如图,在平面直角坐标系中,矩形ABCO的边OA在x轴上,OC在y轴上,OA=a,OC=b(a≤b,a≠0),将矩形ABCO绕点A顺时针旋转90°得到矩形ADEF,双曲线y=(k≠0)经过点B,分别交DE、EF于点P、Q两点.
(1)当a=2,b=4时,求点P、Q的坐标;
(2)当点P是DE的中点时,求证:四边形ABCO是正方形.
26.如图,为等边三角形,点O是角平分线的交点.将绕点O按逆时针方向旋转,分别画出旋转后的图形.
27.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(1)求证:△AMB≌△ENB;
(2)①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
(3)当AM+BM+CM的最小值为时,求正方形的边长.
参考答案:
1.B
【解析】
【详解】
试题分析:根据旋转变换的概念,对选项进行分析,排除错误答案.A、滚动过程中的篮球属于滚动,不是绕着某一个固定的点转动,不属旋转;B、钟表的钟摆的摆动,符合旋转变换的定义,属于旋转;C、气球升空的运动是平移,不属于旋转;D、一个图形沿某直线对折的过程是轴对称,不属于旋转.
故选B.
考点:生活中的旋转现象.
2.C
【解析】
【分析】
将一个图形整体沿某一直线方向移动,得到一个新图形,新图形与原图形的形状和大小完全相同,由此确定C选项与原图形完全相同.
【详解】
通过平移得到的图案是,
故选C.
【点睛】
本题主要考查平移的知识,较简单,掌握平移的定义是关键.
3.A
【解析】
【分析】
根据中心对称图形的概念对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.
【详解】
解:A.是中心对称图形,故本选项符合题意;
B.不是中心对称图形,故本选项不合题意;
C.不是中心对称图形,故本选项不合题意;
D.不是中心对称图形,故本选项不合题意.
故选:A.
【点睛】
本题考查了中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
4.C
【解析】
【分析】
直接利用平移中点的变化规律求解即可.
【详解】
由点A( 1,4)的对应点为A′(1,7)知平移方式为向右平移2个单位、向上平移3个单位,
∴点C( 4, 1)的对应点C′的坐标为( 2,2),
故选C.
【点睛】
此题考查坐标与图形变化-平移,解题关键在于得到平移的方式.
5.D
【解析】
【分析】
根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,据此进行分析即可.
【详解】
解:A.不是轴对称图形,故本选项不合题意;
B.不是轴对称图形,故本选项不合题意;
C.不是轴对称图形,故本选项不合题意;
D.是轴对称图形,故本选项符合题意;
故选:D.
【点睛】
此题主要考查了轴对称图形,正确掌握轴对称图形的定义是解题关键.
6.A
【解析】
【分析】
根据给出的图形先确定出旋转中心,再确定出旋转的方向和度数即可求出答案.
【详解】
根据图形可知:将△ABC绕点A逆时针旋转90°可得到△ADE,点B与点D是对应点,
故选A.
【点睛】
本题主要考查旋转的性质,在解题时,一定要明确三个要素:旋转中心、旋转方向、旋转角度.
7.B
【解析】
【分析】
中心对称图形是在平面内,把一个图形绕某一定点旋转180°,能够与原图形重合的图形.轴对称图形是在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形.依据定义判断.
【详解】
解:A.不是轴对称图形,是中心对称图形,故本选项不合题意;
B.既是轴对称图形,也是中心对称图形,故本选项符合题意;
C.是轴对称图形,不是中心对称图形,故本选项不合题意;
D.是轴对称图形,不是中心对称图形,故本选项不合题意.
故选:B.
【点睛】
本题考查了中心对称图形和轴对称图形的定义,能熟记中心对称图形和轴对称图形的定义是解此题的关键.
8.B
【解析】
【分析】
根据关于原点对称点的坐标变化特征直接判断即可.
【详解】
解:点与点关于原点对称,则点的坐标为,
故选:B.
【点睛】
本题考查了关于原点对称点的坐标,解题关键是明确关于原点对称的两个点横纵坐标都互为相反数.
9.D
【解析】
【分析】
根据旋转的性质和全等三角形的性质逐个判断即可.
【详解】
解:∵将△ABC绕点A旋转后得到△ADE,
∴,
∴,
故A选项正确,不符合题意;
∵,
∴∠E=∠C,
故B选项正确,不符合题意;
∵,
∴,
∴,即,
故C选项正确,不符合题意;
由已知条件无法证明出∠B=∠E,
故D选项错误,符合题意.
故选:D.
【点睛】
此题考查了旋转的性质和全等三角形的性质,解题的关键是熟练掌握旋转的性质和全等三角形的性质.全等三角形的性质:全等三角形对应边相等,对应角相等.
10.D
【解析】
【分析】
由旋转的性质,易得BC=DC=6,由在Rt△ABC中,∠ACB=90°,∠A=30°,即可求得∠B=60°,即可判定△DBC是等边三角形,易得△DFC是含30°角的直角三角形,则可求得DF与FC的长,继而求得阴影部分的面积.
【详解】
解:∵将△ABC绕点C按顺时针方向旋转n度后得到△EDC,
∴BC=DC,
∵在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠B=90°-∠A=60°,
∴△DBC是等边三角形,
∴∠DCB=60°,
∴∠DCA=90°-∠DCB=90°-60°=30°,
∵BC=6,
∴DC=6,
∵∠FDC=∠B=60°,
∴∠DFC=90°,
∴,
∴,
∴S阴影=S△DFC=,
故选:D.
【点睛】
本题考查了旋转的性质、等边三角形的判定与性质、含30°角的直角三角形的性质以及勾股定理,此题综合性较强,难度适中,注意掌握旋转前后图形的对应关系,注意数形结合思想的应用.
11.B
【解析】
【分析】
根据平移、旋转、轴对称的定义逐项判断即可.
【详解】
A、通过旋转得到,故本选项错误,不符合题意;
B、通过平移得到,故本选项正确,符合题意
C、通过轴对称得到,故本选项错误,不符合题意
D、通过旋转得到,故本选项错误,不符合题意
故选:B.
【点睛】
本题考查了平移、旋转、轴对称的定义,解题的关键是熟记定义,平移前后两图形的形状和大小完全相同.
12.B
【解析】
【分析】
根据线段垂直平分线的性质得到AG=BG,根据勾股定理列出方程,解方程得到答案.
【详解】
解:设BG=x,则DG=8﹣x,
由作图可知:EF是线段AB的垂直平分线,
∴AG=BG=x,
在Rt△DAG中,AD2+AG2=DG2,
即42+x2=(8﹣x)2,
解得:x=3,
即AG=3,
故选:B.
【点睛】
本题考查了线段垂直平分线的性质以及勾股定理,根据线段垂直平分线的性质求出AG=BG是解题的关键.
13.A
【解析】
【分析】
由旋转的性质可得△ABC≌△AB'C',∠BAB'=∠CAC'=60°,AB=AB',即可分析求解.
【详解】
∵将△ABC绕点A逆时针旋转60°得到△AB′C′,
∴△ABC≌△AB'C',∠BAB'=∠CAC'=60°,
∴AB=AB',∠CAB'<∠BAB'=60°,
故选:A.
【点睛】
本题考查了旋转的性质,全等三角形的性质,熟练运用旋转的性质是关键.
14.A
【解析】
【分析】
根据平移的性质逐一判断即可.
【详解】
解:经过平移后得到,
∴,故①正确;
,故②正确;
,故③正确;
和的面积相等,故④正确;
四边形和四边形都是平行四边形,且,即两个平行四边形的底相等,但高不一定相等,
∴四边形和四边形的面积不一定相等,故⑤不正确;
综上:正确的有4个
故选A.
【点睛】
此题考查的是图形的平移,掌握平移的性质是解题关键.
15.B
【解析】
【分析】
先求出∠ACD=30°,再根据旋转角求出∠ACD1=45°,然后判断出ACO是等腰直角三角形,再根据等腰直角三角形的性质求出AO、CO,AB⊥CO,再求出D1O然后利用勾股定理列式计算即可求解.
【详解】
解:∵∠ACB=∠DEC=90°,∠D=30°,
∴∠DCE=90°﹣30°=60°,
∴∠ACD=90°﹣60°=30°,
∵旋转角为15°,
∴∠ACD1=30°+15°=45°,
又∵∠CAB=45°,
∴ACO是等腰直角三角形,
∴AO=CO=AB=×12=6,AB⊥CO,
∵DC=14,
∴D1C=DC=14,
∴D1O=14﹣6=8,
在RtAOD1中,AD1===10.
故选:B.
【点睛】
本题考查了旋转的性质,等腰直角三角形的判定和性质,勾股定理的运用,根据等腰直角三角形的性质判断AB⊥CO是解题关键.
16. x轴 原点 y轴
【解析】
【分析】
根据点的坐标平移特点:左减右加,上加下减,以及关于x轴,关于y轴对称和关于原点点的坐标特征进行求解即可.
【详解】
解:把点向下平移4个单位长度,可以得到对应点(3,2-4)即(3,-2);
再向左平移6个单位长度可以得到对应点(3-6,-2)即(-3,-2);则点与点A关于x轴对称;点与点A关于原点对称;点与点关于y轴对称,
故答案为:(3,-2);(-3,-2);x轴;原点;y轴.
【点睛】
本题主要考查了点的坐标平移,关于x轴,关于y轴对称和关于原点点的坐标特征,解题的关键在于能够熟练掌握相关知识进行求解.
17.180
【解析】
【详解】
根据全等三角形的对应关系,可知A与A′是一对对应点,则可知旋转了180°.
故答案为180.
【点睛】
此题主要考查了旋转变化的辨别,解题关键是根据全等三角形确定对应点,从而知与旋转中心构成的角度即可求解,比较简单.
18.﹣﹣1
【解析】
【分析】
根据勾股定理即可得点A表示的数.
【详解】
解:根据勾股定理,得=,=,
∴点A表示的数为:﹣﹣1.
故答案为:﹣﹣1.
【点睛】
本题考查了数轴上的点与实数的关系,以及勾股定理,解决本题的关键是掌握勾股定理.直角三角形两条直角边的平方和等于斜边的平方.
19. 48° 132° 48°
【解析】
【分析】
根据两直线平行内错角相等可求出∠2,根据两直线平行,同位角相等可求出∠4,同旁内角互补可求出∠3.
【详解】
解:∵ //,∠1=48°,
∴∠2=∠1=48°,
∵ //,∠1=48°,
∴∠4=∠1=48°,
∵ //,
∴∠3+∠4=180°
∴∠3=180°-∠4=180°-48°=132°
故答案为:48°;132°;48°
【点睛】
此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键.
20. 旋转中心 旋转方向 旋转角 旋转中心 旋转后的图形
【解析】
略
21.详见解析.
【解析】
【分析】
根据题意画出图象即可.
【详解】
如图所示: 即为所求三角形.
【点睛】
本题考查作图-旋转,关键在于掌握作图技巧.
22.B'(5,5),C'(7,4),D'(9,5),M'(7,5)
【解析】
【分析】
根据菱形的性质得出点C和D的坐标,由点A'的坐标得出将四边形ABCD向右平移4个单位长度,再向上平移3个单位长度,再根据平移的性质即可得出答案.
【详解】
解:∵四边形ABCD四条边相等,
∴四边形ABCD是菱形,
∴AC⊥BD,
∵A (3,3),B(1,2),对角线的交点为M(3,2).
∴C(3,1),D(5,2),
∵将四边形ABCD平移后,顶点A(3,3)的对应点是A'(7,6),
即将四边形ABCD向右平移4个单位长度,再向上平移3个单位长度,
∴平移后点B,C,D,M对应点的坐标分别为B'(1+4,2+3),C'(3+4,1+3),D'(5+4,2+3),M'(3+4,2+3),
即B'(5,5),C'(7,4),D'(9,5),M'(7,5).
【点睛】
本题考查了菱形的性质和判定、平移的性质、坐标与图形性质等知识;熟练掌握菱形的性质和平移的性质,求出C、D的坐标是解题的关键.
23.(1)平移的方向是点A到点D的方向,平移的距离是线段的长度;(2)见解析
【解析】
【分析】
(1)根据题意可知平移的方向和距离;
(2)按照点到点的平移方向和距离,分别平行至,过点B,C分别作线段,使得它们与线段平行且相等,连接即可.
【详解】
解:(1)如图,连接,平移的方向是点A到点D的方向,平移的距离是线段的长度.
(2)如图,过点B,C分别作线段,使得它们与线段平行且相等,连接,就是平移后的图形.
【点睛】
本题考查了平移的性质,平移作图,理解平移的性质是解题的关键.
24.(1)见解析;(2)见解析;(3)将(1)中所画图形沿由A到的方向平移13个单位长度即可得到(2)中所画图形.平移后的点与平移前的对应点相比,横坐标分别减少了12,纵坐标分别增加了5
【解析】
【分析】
(1)根据平面直角坐标系中点的坐标秒点连线即可;
(2)根据平移方式进行平移即可;
(3)根据勾股定义求出的长度,根据平移后点的坐标解答即可.
【详解】
解:(1)(2)如图所示;
(3),
将(1)中所画图形沿由A到的方向平移13个单位长度
即可得到(2)中所画图形.
平移后的点与平移前的对应点相比,
横坐标分别减少了12,纵坐标分别增加了5.
【点睛】
本题考查了坐标系中图形的平移-作图,根据题意画出平移后的图形是解本题的关键.
25.(1)P(6,),Q(4,2);(2)见解析
【解析】
【分析】
(1)根据矩形的性质得到B(2,4),进而即可求得y=,根据反比例函数图象上点的坐标特征,即可求得P、Q的坐标;
(2)易得到P的坐标为(a+b,a),根据反比例函数经过点B和P,即可得到(a+b)×b=ab,整理得,b2=ab,即a=b,得到OA=OC,即可证得四边形ABCO是正方形.
【详解】
解:(1)∵OA=2,OC=4,四边形ABCO是矩形
∴B(2,4),
∵双曲线y=(k≠0)经过点B,
∴k=2×4=8,
∴反比例函数的解析式为y=,
由旋转的性质可得AF=OA=2,
∴Q点的纵坐标为2,
把y=2代入y=得,2=,解得x=4,
∴Q(4,2),
由旋转的性质可得AD=OC=4,
∴OD=2+4=6,
∴P点的横坐标为6,
把x=6代入y=得,y=,
∴P(6,);
(2)由题意可知B(a,b),
∵双曲线y=(k≠0)经过点B,
∴k=ab,
∵AD=OC=b,DE=OA=a,且点P是DE的中点,
∴P(a+b,a),
∵双曲线y=(k≠0)交DE于点P,
∴(a+b)×b=ab,
整理得,b2=ab,即a=b,
∴OA=OC,
∵四边形ABCO是矩形,
∴四边形ABCO是正方形.
【点睛】
本题主要考查了矩形的性质,反比例函数、坐标与图形变化—旋转,正方形的判定等等,根据矩形的性质表示出点的坐标是解题的关键.
26.见解析
【解析】
【分析】
连接,根据旋转的性质,即可将△ABC绕点O按逆时针方向旋转,分别画出旋转30°、60°、90°后的图形.
【详解】
解:如图,连接,
△ABC绕点O按逆时针方向旋转,旋转30°、60°、90°后的图形分别为:
△DEF,△,△PQG.
【点睛】
本题考查了作图-旋转变换,解决本题的关键是掌握旋转的性质,等边三角形的性质.
27.(1)见解析;(2)①当M点落在BD的中点时;②当M点位于BD与CE的交点处时,AM+BM+CM的值最小,理由见解析;(3)
【解析】
【分析】
(1)由题意得,,所以,容易证出;
(2)①根据“两点之间线段最短”,可得,当点落在的中点时,的值最小;
②根据“两点之间线段最短”,当点位于与的交点处时,的值最小,即等于的长(如图);
(3)作辅助线,过点作交的延长线于,由题意求出,设正方形的边长为,在中,根据勾股定理求得正方形的边长为.
【详解】
(1)证明:是等边三角形,
,.
,
.
即.
又,
.
(2)解:①当点落在的中点时,、、三点共线,的值最小.②如图,连接,当点位于与的交点处时,
的值最小,
理由如下:连接,由(1)知,,
,
,,
是等边三角形.
.
.
根据“两点之间线段最短”可知,若、、、在同一条直线上时,取得最小值,最小值为.
在和中,
,
,
,
,
,
若连接,则,
,,
、可以同时在直线上.
当点位于与的交点处时,的值最小,即等于的长.
(3)解:过点作交的延长线于,
.
设正方形的边长为,则,.
在中,
,
.
解得,(舍去负值).
正方形的边长为.
【点睛】
本题考查轴对称的性质和正方形的性质,旋转的性质,三角形全等,等边三角形,解题的关键是添加适当辅助线,利用运用相关定理求解,是一道综合性的题目,难度很大.
一、单选题
1.下列运动是属于旋转的是( )
A.滚动过程中的篮球的滚动; B.钟表的钟摆的摆动;
C.气球升空的运动; D.一个图形沿某直线对折过程
2.2019年10月18日,第七届军人运动会在武汉举行,如图是第七届运动会的吉祥物兵兵,下列图案中,是通过平移得到的图案是( )
A. B. C. D.
3.下列四个生活安全警示图标,其中是中心对称图形的是( )
A. B. C. D.
4.是由平移得到的,点的对应点为,点的对应点为,则点的对应点的坐标为( )
A. B. C. D.
5.将如图的七巧板的其中几块,拼成一个多边形,为轴对称图形的是( )
A. B.
C. D.
6.如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是( )
A.逆时针旋转90° B.顺时针旋转90° C.逆时针旋转45° D.顺时针旋转45°
7.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
8.已知点与点关于原点对称,则点的坐标( )
A. B. C. D.
9.如图,将△ABC绕点A旋转后得到△ADE,则下列结论不正确的是( )
A.BC=DE B.∠E=∠C C.∠EAC=∠BAD D.∠B=∠E
10.如图,在中,.将绕点按顺时针方向旋转 度后得到,此时点在边上,斜边交边于点,则图中阴影部分的面积为( )
A.27 B.9 C. D.
11.下列哪些图形是通过平移可以得到的( )
A. B.
C. D.
12.如图,在 ABCD中,AD=4,对角线BD=8,分别以点A、B为圆心,以大于AB的长为半径画弧,两弧相交于点E和点F,作直线EF,交对角线BD于点G,连接GA,GA恰好垂直于边AD,则GA的长是( )
A.2 B.3 C.4 D.5
13.如图,将绕点逆时针旋转得到,则下列说法中,不正确的是( )
A. B. C. D.
14.如图,经过平移后得到,下列说法:
①
②
③
④和的面积相等
⑤四边形和四边形的面积相等,其中正确的有( )
A.个 B.个 C.个 D.个
15.把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,DC=14,把三角板DCE绕点C顺时针旋转15°得到D1CE1(如图乙),此时AB与 CD1交于点O,则线段AD1的长为( )
A.6 B.10 C.8 D.
二、填空题
16.把点向下平移4个单位长度,可以得到对应点______,再向左平移6个单位长度可以得到对应点_______,则点与点A关于________对称,点与点A关于_________对称,点与点关于_______对称.
17.如图所示,△ABC与△A′B′C′是全等三角形,那么△A′B′C′可以看作是由△ABC以O为旋转中心,旋转_______度形成的.
18.如图:点A表示的数为__.
19.如图,已知,且∠1=48°,则∠2=_____,∠3=_____,∠4=_____.
20.旋转作图的基本步骤:
(1)确定___________、_____________和____________;
(2)找出图形的关键点,一般是图形中的转折点,例如,多边形的关键点 是它的顶点.
(3)作旋转后的对应点,方法如下:
①连:连接图形的每个关键点与__________;
②转:把连线绕旋转中心按旋转方向旋转相同的角度(作旋转角);
③截:在作得的角的另一边截取与关键点到旋转中心的距离相等的线段,得到各个关键点的对应点;
(4)按原图形的顺序连接这些对应点,所得到的图形就是___________.
(5)写出结论,说明作出的图形即为所求的图形.
三、解答题
21.如图,已知和点请画出绕点顺时针旋转后得到的
22.已知四边形四条边相等,它的两个顶点坐标分别为,对角线的交点为.将四边形平移后,顶点A的对应点是,请写出点B,C,D,M对应点的坐标.
23.如图,经过平移,的顶点A移到了点D.
(1)指出平移的方向和平移的距离;
(2)画出平移后的三角形.
24.(1)在平面直角坐标系中描出点,然后用线段依次连接A,B,C,D,E,F,A各点;
(2)将(1)中所画图形先向左平移12个单位长度,再向上平移5个单位长度,画出第二次平移后的图形;
(3)如何将(1)中所画图形经过一次平移得到(2)中所画图形?平移前后对应点的横坐标有什么关系?纵坐标呢?
25.如图,在平面直角坐标系中,矩形ABCO的边OA在x轴上,OC在y轴上,OA=a,OC=b(a≤b,a≠0),将矩形ABCO绕点A顺时针旋转90°得到矩形ADEF,双曲线y=(k≠0)经过点B,分别交DE、EF于点P、Q两点.
(1)当a=2,b=4时,求点P、Q的坐标;
(2)当点P是DE的中点时,求证:四边形ABCO是正方形.
26.如图,为等边三角形,点O是角平分线的交点.将绕点O按逆时针方向旋转,分别画出旋转后的图形.
27.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(1)求证:△AMB≌△ENB;
(2)①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
(3)当AM+BM+CM的最小值为时,求正方形的边长.
参考答案:
1.B
【解析】
【详解】
试题分析:根据旋转变换的概念,对选项进行分析,排除错误答案.A、滚动过程中的篮球属于滚动,不是绕着某一个固定的点转动,不属旋转;B、钟表的钟摆的摆动,符合旋转变换的定义,属于旋转;C、气球升空的运动是平移,不属于旋转;D、一个图形沿某直线对折的过程是轴对称,不属于旋转.
故选B.
考点:生活中的旋转现象.
2.C
【解析】
【分析】
将一个图形整体沿某一直线方向移动,得到一个新图形,新图形与原图形的形状和大小完全相同,由此确定C选项与原图形完全相同.
【详解】
通过平移得到的图案是,
故选C.
【点睛】
本题主要考查平移的知识,较简单,掌握平移的定义是关键.
3.A
【解析】
【分析】
根据中心对称图形的概念对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.
【详解】
解:A.是中心对称图形,故本选项符合题意;
B.不是中心对称图形,故本选项不合题意;
C.不是中心对称图形,故本选项不合题意;
D.不是中心对称图形,故本选项不合题意.
故选:A.
【点睛】
本题考查了中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
4.C
【解析】
【分析】
直接利用平移中点的变化规律求解即可.
【详解】
由点A( 1,4)的对应点为A′(1,7)知平移方式为向右平移2个单位、向上平移3个单位,
∴点C( 4, 1)的对应点C′的坐标为( 2,2),
故选C.
【点睛】
此题考查坐标与图形变化-平移,解题关键在于得到平移的方式.
5.D
【解析】
【分析】
根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,据此进行分析即可.
【详解】
解:A.不是轴对称图形,故本选项不合题意;
B.不是轴对称图形,故本选项不合题意;
C.不是轴对称图形,故本选项不合题意;
D.是轴对称图形,故本选项符合题意;
故选:D.
【点睛】
此题主要考查了轴对称图形,正确掌握轴对称图形的定义是解题关键.
6.A
【解析】
【分析】
根据给出的图形先确定出旋转中心,再确定出旋转的方向和度数即可求出答案.
【详解】
根据图形可知:将△ABC绕点A逆时针旋转90°可得到△ADE,点B与点D是对应点,
故选A.
【点睛】
本题主要考查旋转的性质,在解题时,一定要明确三个要素:旋转中心、旋转方向、旋转角度.
7.B
【解析】
【分析】
中心对称图形是在平面内,把一个图形绕某一定点旋转180°,能够与原图形重合的图形.轴对称图形是在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形.依据定义判断.
【详解】
解:A.不是轴对称图形,是中心对称图形,故本选项不合题意;
B.既是轴对称图形,也是中心对称图形,故本选项符合题意;
C.是轴对称图形,不是中心对称图形,故本选项不合题意;
D.是轴对称图形,不是中心对称图形,故本选项不合题意.
故选:B.
【点睛】
本题考查了中心对称图形和轴对称图形的定义,能熟记中心对称图形和轴对称图形的定义是解此题的关键.
8.B
【解析】
【分析】
根据关于原点对称点的坐标变化特征直接判断即可.
【详解】
解:点与点关于原点对称,则点的坐标为,
故选:B.
【点睛】
本题考查了关于原点对称点的坐标,解题关键是明确关于原点对称的两个点横纵坐标都互为相反数.
9.D
【解析】
【分析】
根据旋转的性质和全等三角形的性质逐个判断即可.
【详解】
解:∵将△ABC绕点A旋转后得到△ADE,
∴,
∴,
故A选项正确,不符合题意;
∵,
∴∠E=∠C,
故B选项正确,不符合题意;
∵,
∴,
∴,即,
故C选项正确,不符合题意;
由已知条件无法证明出∠B=∠E,
故D选项错误,符合题意.
故选:D.
【点睛】
此题考查了旋转的性质和全等三角形的性质,解题的关键是熟练掌握旋转的性质和全等三角形的性质.全等三角形的性质:全等三角形对应边相等,对应角相等.
10.D
【解析】
【分析】
由旋转的性质,易得BC=DC=6,由在Rt△ABC中,∠ACB=90°,∠A=30°,即可求得∠B=60°,即可判定△DBC是等边三角形,易得△DFC是含30°角的直角三角形,则可求得DF与FC的长,继而求得阴影部分的面积.
【详解】
解:∵将△ABC绕点C按顺时针方向旋转n度后得到△EDC,
∴BC=DC,
∵在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠B=90°-∠A=60°,
∴△DBC是等边三角形,
∴∠DCB=60°,
∴∠DCA=90°-∠DCB=90°-60°=30°,
∵BC=6,
∴DC=6,
∵∠FDC=∠B=60°,
∴∠DFC=90°,
∴,
∴,
∴S阴影=S△DFC=,
故选:D.
【点睛】
本题考查了旋转的性质、等边三角形的判定与性质、含30°角的直角三角形的性质以及勾股定理,此题综合性较强,难度适中,注意掌握旋转前后图形的对应关系,注意数形结合思想的应用.
11.B
【解析】
【分析】
根据平移、旋转、轴对称的定义逐项判断即可.
【详解】
A、通过旋转得到,故本选项错误,不符合题意;
B、通过平移得到,故本选项正确,符合题意
C、通过轴对称得到,故本选项错误,不符合题意
D、通过旋转得到,故本选项错误,不符合题意
故选:B.
【点睛】
本题考查了平移、旋转、轴对称的定义,解题的关键是熟记定义,平移前后两图形的形状和大小完全相同.
12.B
【解析】
【分析】
根据线段垂直平分线的性质得到AG=BG,根据勾股定理列出方程,解方程得到答案.
【详解】
解:设BG=x,则DG=8﹣x,
由作图可知:EF是线段AB的垂直平分线,
∴AG=BG=x,
在Rt△DAG中,AD2+AG2=DG2,
即42+x2=(8﹣x)2,
解得:x=3,
即AG=3,
故选:B.
【点睛】
本题考查了线段垂直平分线的性质以及勾股定理,根据线段垂直平分线的性质求出AG=BG是解题的关键.
13.A
【解析】
【分析】
由旋转的性质可得△ABC≌△AB'C',∠BAB'=∠CAC'=60°,AB=AB',即可分析求解.
【详解】
∵将△ABC绕点A逆时针旋转60°得到△AB′C′,
∴△ABC≌△AB'C',∠BAB'=∠CAC'=60°,
∴AB=AB',∠CAB'<∠BAB'=60°,
故选:A.
【点睛】
本题考查了旋转的性质,全等三角形的性质,熟练运用旋转的性质是关键.
14.A
【解析】
【分析】
根据平移的性质逐一判断即可.
【详解】
解:经过平移后得到,
∴,故①正确;
,故②正确;
,故③正确;
和的面积相等,故④正确;
四边形和四边形都是平行四边形,且,即两个平行四边形的底相等,但高不一定相等,
∴四边形和四边形的面积不一定相等,故⑤不正确;
综上:正确的有4个
故选A.
【点睛】
此题考查的是图形的平移,掌握平移的性质是解题关键.
15.B
【解析】
【分析】
先求出∠ACD=30°,再根据旋转角求出∠ACD1=45°,然后判断出ACO是等腰直角三角形,再根据等腰直角三角形的性质求出AO、CO,AB⊥CO,再求出D1O然后利用勾股定理列式计算即可求解.
【详解】
解:∵∠ACB=∠DEC=90°,∠D=30°,
∴∠DCE=90°﹣30°=60°,
∴∠ACD=90°﹣60°=30°,
∵旋转角为15°,
∴∠ACD1=30°+15°=45°,
又∵∠CAB=45°,
∴ACO是等腰直角三角形,
∴AO=CO=AB=×12=6,AB⊥CO,
∵DC=14,
∴D1C=DC=14,
∴D1O=14﹣6=8,
在RtAOD1中,AD1===10.
故选:B.
【点睛】
本题考查了旋转的性质,等腰直角三角形的判定和性质,勾股定理的运用,根据等腰直角三角形的性质判断AB⊥CO是解题关键.
16. x轴 原点 y轴
【解析】
【分析】
根据点的坐标平移特点:左减右加,上加下减,以及关于x轴,关于y轴对称和关于原点点的坐标特征进行求解即可.
【详解】
解:把点向下平移4个单位长度,可以得到对应点(3,2-4)即(3,-2);
再向左平移6个单位长度可以得到对应点(3-6,-2)即(-3,-2);则点与点A关于x轴对称;点与点A关于原点对称;点与点关于y轴对称,
故答案为:(3,-2);(-3,-2);x轴;原点;y轴.
【点睛】
本题主要考查了点的坐标平移,关于x轴,关于y轴对称和关于原点点的坐标特征,解题的关键在于能够熟练掌握相关知识进行求解.
17.180
【解析】
【详解】
根据全等三角形的对应关系,可知A与A′是一对对应点,则可知旋转了180°.
故答案为180.
【点睛】
此题主要考查了旋转变化的辨别,解题关键是根据全等三角形确定对应点,从而知与旋转中心构成的角度即可求解,比较简单.
18.﹣﹣1
【解析】
【分析】
根据勾股定理即可得点A表示的数.
【详解】
解:根据勾股定理,得=,=,
∴点A表示的数为:﹣﹣1.
故答案为:﹣﹣1.
【点睛】
本题考查了数轴上的点与实数的关系,以及勾股定理,解决本题的关键是掌握勾股定理.直角三角形两条直角边的平方和等于斜边的平方.
19. 48° 132° 48°
【解析】
【分析】
根据两直线平行内错角相等可求出∠2,根据两直线平行,同位角相等可求出∠4,同旁内角互补可求出∠3.
【详解】
解:∵ //,∠1=48°,
∴∠2=∠1=48°,
∵ //,∠1=48°,
∴∠4=∠1=48°,
∵ //,
∴∠3+∠4=180°
∴∠3=180°-∠4=180°-48°=132°
故答案为:48°;132°;48°
【点睛】
此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键.
20. 旋转中心 旋转方向 旋转角 旋转中心 旋转后的图形
【解析】
略
21.详见解析.
【解析】
【分析】
根据题意画出图象即可.
【详解】
如图所示: 即为所求三角形.
【点睛】
本题考查作图-旋转,关键在于掌握作图技巧.
22.B'(5,5),C'(7,4),D'(9,5),M'(7,5)
【解析】
【分析】
根据菱形的性质得出点C和D的坐标,由点A'的坐标得出将四边形ABCD向右平移4个单位长度,再向上平移3个单位长度,再根据平移的性质即可得出答案.
【详解】
解:∵四边形ABCD四条边相等,
∴四边形ABCD是菱形,
∴AC⊥BD,
∵A (3,3),B(1,2),对角线的交点为M(3,2).
∴C(3,1),D(5,2),
∵将四边形ABCD平移后,顶点A(3,3)的对应点是A'(7,6),
即将四边形ABCD向右平移4个单位长度,再向上平移3个单位长度,
∴平移后点B,C,D,M对应点的坐标分别为B'(1+4,2+3),C'(3+4,1+3),D'(5+4,2+3),M'(3+4,2+3),
即B'(5,5),C'(7,4),D'(9,5),M'(7,5).
【点睛】
本题考查了菱形的性质和判定、平移的性质、坐标与图形性质等知识;熟练掌握菱形的性质和平移的性质,求出C、D的坐标是解题的关键.
23.(1)平移的方向是点A到点D的方向,平移的距离是线段的长度;(2)见解析
【解析】
【分析】
(1)根据题意可知平移的方向和距离;
(2)按照点到点的平移方向和距离,分别平行至,过点B,C分别作线段,使得它们与线段平行且相等,连接即可.
【详解】
解:(1)如图,连接,平移的方向是点A到点D的方向,平移的距离是线段的长度.
(2)如图,过点B,C分别作线段,使得它们与线段平行且相等,连接,就是平移后的图形.
【点睛】
本题考查了平移的性质,平移作图,理解平移的性质是解题的关键.
24.(1)见解析;(2)见解析;(3)将(1)中所画图形沿由A到的方向平移13个单位长度即可得到(2)中所画图形.平移后的点与平移前的对应点相比,横坐标分别减少了12,纵坐标分别增加了5
【解析】
【分析】
(1)根据平面直角坐标系中点的坐标秒点连线即可;
(2)根据平移方式进行平移即可;
(3)根据勾股定义求出的长度,根据平移后点的坐标解答即可.
【详解】
解:(1)(2)如图所示;
(3),
将(1)中所画图形沿由A到的方向平移13个单位长度
即可得到(2)中所画图形.
平移后的点与平移前的对应点相比,
横坐标分别减少了12,纵坐标分别增加了5.
【点睛】
本题考查了坐标系中图形的平移-作图,根据题意画出平移后的图形是解本题的关键.
25.(1)P(6,),Q(4,2);(2)见解析
【解析】
【分析】
(1)根据矩形的性质得到B(2,4),进而即可求得y=,根据反比例函数图象上点的坐标特征,即可求得P、Q的坐标;
(2)易得到P的坐标为(a+b,a),根据反比例函数经过点B和P,即可得到(a+b)×b=ab,整理得,b2=ab,即a=b,得到OA=OC,即可证得四边形ABCO是正方形.
【详解】
解:(1)∵OA=2,OC=4,四边形ABCO是矩形
∴B(2,4),
∵双曲线y=(k≠0)经过点B,
∴k=2×4=8,
∴反比例函数的解析式为y=,
由旋转的性质可得AF=OA=2,
∴Q点的纵坐标为2,
把y=2代入y=得,2=,解得x=4,
∴Q(4,2),
由旋转的性质可得AD=OC=4,
∴OD=2+4=6,
∴P点的横坐标为6,
把x=6代入y=得,y=,
∴P(6,);
(2)由题意可知B(a,b),
∵双曲线y=(k≠0)经过点B,
∴k=ab,
∵AD=OC=b,DE=OA=a,且点P是DE的中点,
∴P(a+b,a),
∵双曲线y=(k≠0)交DE于点P,
∴(a+b)×b=ab,
整理得,b2=ab,即a=b,
∴OA=OC,
∵四边形ABCO是矩形,
∴四边形ABCO是正方形.
【点睛】
本题主要考查了矩形的性质,反比例函数、坐标与图形变化—旋转,正方形的判定等等,根据矩形的性质表示出点的坐标是解题的关键.
26.见解析
【解析】
【分析】
连接,根据旋转的性质,即可将△ABC绕点O按逆时针方向旋转,分别画出旋转30°、60°、90°后的图形.
【详解】
解:如图,连接,
△ABC绕点O按逆时针方向旋转,旋转30°、60°、90°后的图形分别为:
△DEF,△,△PQG.
【点睛】
本题考查了作图-旋转变换,解决本题的关键是掌握旋转的性质,等边三角形的性质.
27.(1)见解析;(2)①当M点落在BD的中点时;②当M点位于BD与CE的交点处时,AM+BM+CM的值最小,理由见解析;(3)
【解析】
【分析】
(1)由题意得,,所以,容易证出;
(2)①根据“两点之间线段最短”,可得,当点落在的中点时,的值最小;
②根据“两点之间线段最短”,当点位于与的交点处时,的值最小,即等于的长(如图);
(3)作辅助线,过点作交的延长线于,由题意求出,设正方形的边长为,在中,根据勾股定理求得正方形的边长为.
【详解】
(1)证明:是等边三角形,
,.
,
.
即.
又,
.
(2)解:①当点落在的中点时,、、三点共线,的值最小.②如图,连接,当点位于与的交点处时,
的值最小,
理由如下:连接,由(1)知,,
,
,,
是等边三角形.
.
.
根据“两点之间线段最短”可知,若、、、在同一条直线上时,取得最小值,最小值为.
在和中,
,
,
,
,
,
若连接,则,
,,
、可以同时在直线上.
当点位于与的交点处时,的值最小,即等于的长.
(3)解:过点作交的延长线于,
.
设正方形的边长为,则,.
在中,
,
.
解得,(舍去负值).
正方形的边长为.
【点睛】
本题考查轴对称的性质和正方形的性质,旋转的性质,三角形全等,等边三角形,解题的关键是添加适当辅助线,利用运用相关定理求解,是一道综合性的题目,难度很大.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
