北师大版八年级数学下册同步练习第6章平行四边形复习题(word,含答案)
文档属性
| 名称 | 北师大版八年级数学下册同步练习第6章平行四边形复习题(word,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 500.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 09:19:55 | ||
图片预览




文档简介
北师大版八年级数学下册同步练习 第6章 平行四边形 复习题
一、单选题
1.内角和与外角和相等的图形是( )
A.三角形 B.四边形 C.五边形 D.六边形
2.判断下列命题正确的是( )
A.两条直线被第三条直线所截,同旁内角互补 B.三角形的三条高都在三角形的内部
C.平移前后图形的形状和大小都没有发生改变 D.过一点有且只有一条直线与已知直线平行
3.如图是平行四边形的边延长线上的一点,交于点,下列各式中错误的是( ).
A. B. C. D.
4.若一个正多边形的每个内角度数都为135°,则这个正多边形的边数是( )
A.6 B.8 C.10 D.12
5.已知∠AOB=100°,过点O作射线OC、OM,使∠AOC=20°,OM是∠BOC的平分线,则∠BOM的度数为( )
A.60° B.60°或40° C.120°或80° D.40°
6.在平面直角坐标系中,A,B,C三点的坐标分别为(0,0),(0,-5),(-2,-2),以这三点为平行四边形的三个顶点,则第四个顶点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如图,在平行四边形ABCD中,已知AD=6cm,AB=4cm,则平行四边形ABCD的周长为( )
A.6cm B.10cm C.12cm D.20cm
8.如图,D,E分别是△ABC的边AB,AC的中点,H,G是边BC上的点,且HG=BC,S△ABC=24,则图中阴影部分的面积为( )
A.4 B.6 C.8 D.12
9.下列命题是假命题的是( )
A.平行四边形的对角线互相平分 B.矩形的对角线互相垂直
C.菱形的对角线互相垂直平分 D.正方形的对角线互相垂直平分且相等
10.如图,平行四边形ABCD的对角线AC,BD相交于点O,CE平分交BD于点F,且,,连接OE,下列结论:①;②;③.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
二、填空题
11.如果一个多边形的每个外角都是40°,那么这个多边形是________边形.
12.如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=9cm,DE=4cm,求CE的长为__cm.
13. ABCD的对角线交于点O,S△AOB=2cm2,则S ABCD=________.
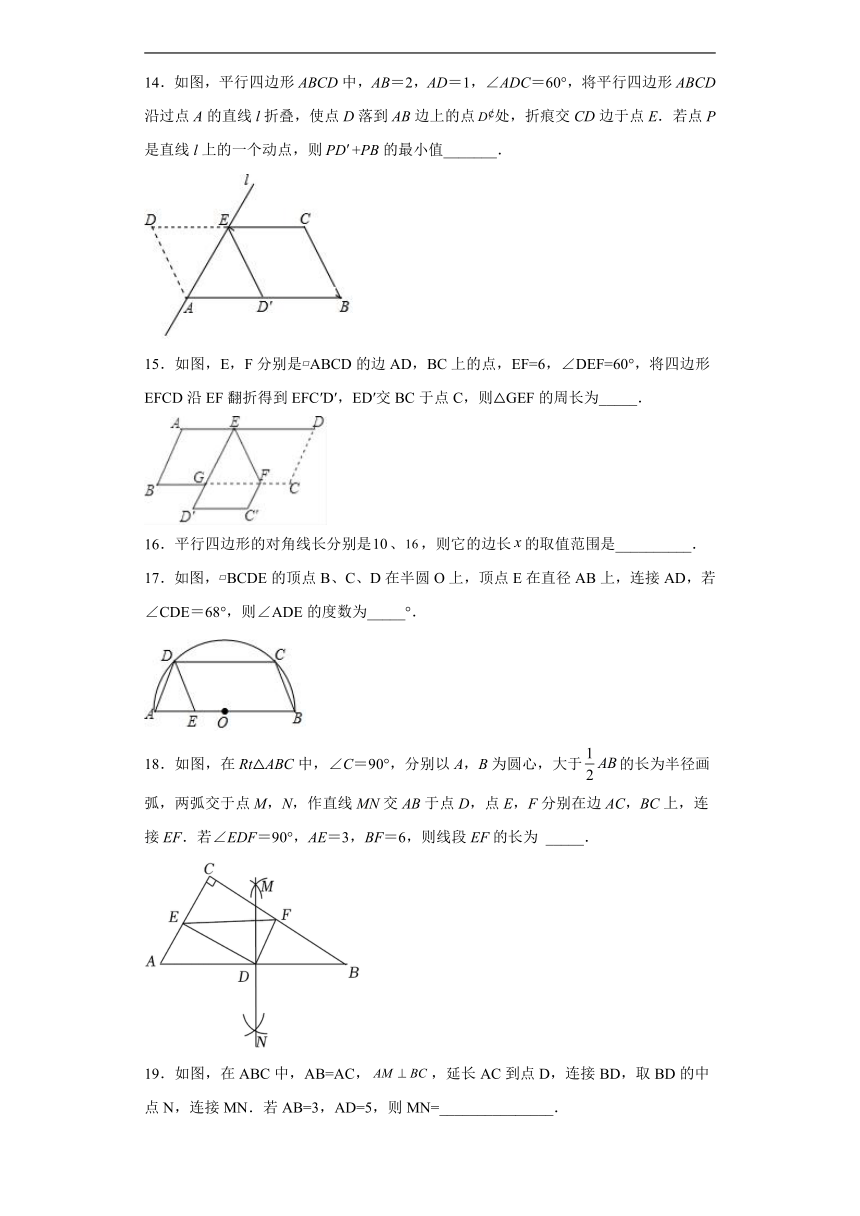
14.如图,平行四边形ABCD中,AB=2,AD=1,∠ADC=60°,将平行四边形ABCD沿过点A的直线l折叠,使点D落到AB边上的点处,折痕交CD边于点E.若点P是直线l上的一个动点,则+PB的最小值_______.
15.如图,E,F分别是 ABCD的边AD,BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折得到EFC′D′,ED′交BC于点C,则△GEF的周长为_____.
16.平行四边形的对角线长分别是、,则它的边长的取值范围是__________.
17.如图, BCDE的顶点B、C、D在半圆O上,顶点E在直径AB上,连接AD,若∠CDE=68°,则∠ADE的度数为_____°.
18.如图,在Rt△ABC中,∠C=90°,分别以A,B为圆心,大于的长为半径画弧,两弧交于点M,N,作直线MN交AB于点D,点E,F分别在边AC,BC上,连接EF.若∠EDF=90°,AE=3,BF=6,则线段EF的长为 _____.
19.如图,在ABC中,AB=AC,,延长AC到点D,连接BD,取BD的中点N,连接MN.若AB=3,AD=5,则MN=_______________.
20.如图,在△ABC中,CA=CB,∠ACB=120°,E为AB上一点,∠DCE=∠DAE=60°,AD=2.4,BE=7,则DE=_____.
三、解答题
21.如图所示,在中,两条对角线相交于点,点、、、分别是、、、的中点,以图中的任意四点(即点、、、、、、、、中的任意四点)为顶点画两种不同的平行四边形.
22.【阅读理解】我们知道,利用相似三角形性质求线段长是常用求线段长的方法之一,如图①,在△ABC中,D为BC上一点,若∠BAD=∠C,可易证△ABD∽△CBA,从而可得AB2=BD·BC,若已知其中两条线段的长即可求出第三条线段的长.
(1)【尝试应用】如图②,在 BCEF中,D为BC上一点,E为AC上一点,∠BAD=∠C,若AB=8,BD=5,求EF的长.
(2)【拓展应用】如图③,在正方形ABCD中,E是AB上一点,F是△ABC内一点,EFAC,∠EDF=45°,EF=8,DE=12,请求出正方形ABCD的边长.
23.如图,在△ABC中,M、N分别为AB、AC边上的中点.D、E为BC边上的两点,且DE=BD+EC,ME与ND交于点O,请你写出图中一对全等的三角形,并加以证明.
24.如图,在Rt△ABC中,∠C=90°,∠BAC=60°,AM平分∠BAC,AM的长为15cm,求BC的长.
25.已知:菱形ABCD的对角线AC,BD交于点O,CE∥OD,DE∥OC.求证:四边形OCED是矩形.
26.如图(1),正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接DE,过点A作AM⊥DE,垂足为M,AM与BD相交于点F.
(1)直接写出OE与OF的数量关系: ;
(2)如图(2)若点E在AC的延长线上,AM⊥DE于点M,AM交BD的延长线于点F,其他条件不变.试探究OE与OF的数量关系,并说明理由.
27.如图,四边形和四边形都是平行四边形,点R为的中点,分别交和于点P,Q,求.
参考答案:
1.B
【解析】
【分析】
设多边形有n条边,则内角和为180°(n-2),再根据内角和等于外角和可得方程180°(n-2)=360°,再解方程即可.
【详解】
解:设多边形有n条边,由题意得:
180°(n-2)=360°
解得:n=4,
故选:B.
【点睛】
此题主要考查了多边形的内角和和外角和,关键是掌握内角和为180°(n-2).
2.C
【解析】
【分析】
利用平移的性质以及三角形的高和平行线的性质分别进行判断即可.
【详解】
解:A、根据两条平行直线被第三条直线所截,同旁内角互补,故此选项错误;
B、钝角三角形的高可以在三角形的外部,故此选项错误;
C、根据平移的性质,平移前后图形的形状和大小都没有发生改变,故此选项正确;
D、过直线外一点有且只有一条直线与已知直线平行,故此选项错误.
故选:C.
【点睛】
此题主要考查了命题与定理,熟练利用相关定理与性质判断是解题关键.
3.D
【解析】
【分析】
根据平行四边形的性质和相似三角形的性质,逐一判断各个选项,即可.
【详解】
解:∵在平行四边形中,AD∥BC,
∴,A选项正确,不符合题意;
∵CD∥BE,
∴△CDF∽△EAF,
∴,
∵AB=CD,
∴,C选项正确,不符合题意;
∵CD∥BE,
∴∠E=∠FCD,
又∵∠B=∠D,
∴△CDF∽△EBC,
∴,B选项正确,不符合题意;
∵AD∥BC,
∴△AEF∽△EBC,
∴,
∴D错误.
故选:D.
【点睛】
此题主要考查了平行四边形、相似三角形的性质,熟练掌握相似三角形的判定和性质,是解题的关键.
4.B
【解析】
【分析】
根据题意可先求出这个正多边形的每个外角度数,再根据多边形的外角和是360°即可求出答案.
【详解】
解:因为一个正多边形的每个内角度数都为135°,
所以这个正多边形的每个外角度数都为45°,
所以这个正多边形的边数是360°÷45°=8.
故选:B.
【点睛】
本题考查了正多边形的有关概念和多边形的外角和,属于基本题目,熟练掌握多边形的基本知识是解题的关键.
5.B
【解析】
【分析】
分两种情况求解:①当OC在∠AOB内部时,②当OC在∠AOB外部时;分别求出∠BOM的度数即可.
【详解】
解:如图1,当OC在∠AOB内部时,
∵∠AOB=100°,∠AOC=20°,
∴∠BOC=80°,
∵OM是∠BOC的平分线,
∴∠BOM=40°;
如图,当OC在∠AOB外部时,
∵∠AOB=100°,∠AOC=20°,
∴∠BOC=120°,
∵OM是∠BOC的平分线,
∴∠BOM=60°;
综上所述:∠BOM的度数为40°或60°,
故选:B.
【点睛】
本题考察了角的计算,熟练掌握角平分线的性质,分两种情况画出图形是解题的关键.
6.A
【解析】
【分析】
已知线段AB,BC,AC,分别以三条线段为平行四边形的对角线,进行分类讨论,结合图形进行判断.
【详解】
如果以线段AB为对角线,AC,BC为边,作平行四边形,则第四个顶点在第四象限;
如果以线段AC为对角线,AB,BC为边,作平行四边形,则第四个顶点在第二象限;
如果以线段CB为对角线,AC,BA为边,作平行四边形,则第四个顶点在第三象限.
故不可能在第一象限.
故选A.
【点睛】
考查了平行四边形的性质,建立平面直角坐标系,数形结合,分类讨论是解题的关键.
7.D
【解析】
【分析】
根据平行四边形的性质:两组对边分别相等,即可求出周长.
【详解】
∵四边形ABCD是平行四边形,
∴BC=AD=6cm,CD=AB=4cm,
∴平行四边形ABCD的周长为(6+4)×2=20(cm),
故选:D.
【点睛】
本题考查了平行四边形的性质,熟练掌握平行四边形的性质是解答的关键.
8.D
【解析】
【分析】
连接DE,作AF⊥BC于F,根据三角形中位线定理得出DE=BC,DE∥BC,根据相似三角形的判定定理和性质定理,结合三角形面积计算即可.
【详解】
解:连接DE,作AF⊥BC于F,如图所示:
∵D,E分别是AB,AC的中点,
∴DE=BC,DE∥BC,AH=FH,
∴△ADE∽△ABC,AH⊥DE,
∴△ADE的面积=24×=6,
∴四边形DBCE的面积=24﹣6=18,
∵HG=BC,
∴DE=HG,
∴△DOE的面积+△HOG的面积=2×DE×AH=△ADE的面积=6,
∴图中阴影部分的面积=18﹣6=12,
故选D.
【点睛】
本题考查的是三角形中位线定理、相似三角形的判定和性质,掌握三角形的中位线定理,证明三角形相似是解题的关键.
9.B
【解析】
【分析】
利用平行四边形、矩形、菱形、正方形的性质解题即可.
【详解】
解:A、正确,平行四边形的对角线互相平分,故选项不符合;
B、错误,应该是矩形的对角线相等且互相平分,故选项符合;
C、正确,菱形的对角线互相垂直且平分,故选项不符合;
D、正确,正方形的对角线相等且互相垂直平分,故选项不符合;
故选:B.
【点睛】
本题考查命题与定理、特殊四边形的性质等知识,解题的关键是熟练掌握特殊四边形的性质,属于中考常考题型.
10.C
【解析】
【分析】
由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据角平分线的定义得到∠DCE=∠BCE=60°推出△CBE是等边三角形,证得∠ACB=90°,求出∠ACD=∠CAB=30°,故①正确;由AC⊥BC,得到S ABCD=AC BC,故②正确,根据直角三角形的性质得到,根据三角形的中位线的性质得到OE=BC,于是得到OE:AC=∶6;故③错误;
【详解】
解:∵四边形ABCD是平行四边形,
,
∵CE平分交AB于点E,
∴,
∴是等边三角形,
∴.
∵,
∴,
∴,
∴,故①正确;
∵,
∴,故②正确;
在中,,,
∴.
,,
∴,
,故③错误.
故选:C.
【点睛】
此题考查了平行四边形的性质、三角形中位线的性质以及等边三角形的判定与性质.注意证得△BCE是等边三角形,OE是△ABC的中位线是关键.
11.九
【解析】
【分析】
根据多边形的外角和是360度即可求得外角的个数,即多边形的边数.
【详解】
解:多边形的边数是:,
故答案为:九.
【点睛】
本题主要考查了多边形的外角和定理,理解多边形外角和中外角的个数与正多边形的边数之间的关系,是解题关键.
12.5.
【解析】
【分析】
根据角平分线和平行线的性质可证BD=FD,EF=CE,再根据线段和差可求CE的长.
【详解】
解:∵BF、CF分别平分∠ABC、∠ACG,
∴∠DBF=∠CBF,∠FCE=∠FCG,
∵DE∥BC,
∴∠DFB=∠CBF,∠EFC=∠FCG,
∴∠DBF=∠DFB,∠FCE=∠EFC,
∴BD=FD,EF=CE,
∵BD=9cm,DE=4cm,,
∴EF=DF﹣DE=BD﹣DE=9﹣4=5(cm),
∴EC=5cm,
故答案为:5.
【点睛】
本题考查了平行线的性质、角平分线的定义和等腰三角形的判定,解题关键是理解已知条件,根据角平分线和平行线得出等腰三角形.
13.
【解析】
【分析】
因为平行四边形的对角线互相平分,所以对角线分成的四个三角形的面积相等,即可得出答案.
【详解】
解:如图所示:∵四边形ABCD是平行四边形,
∴S△ABC=S△ADC,△AOB≌△DOC,△AOD≌△BOC,
∴S△AOB=S△DOC,S△AOD=S△BOC,
∵OA=OC,
∴S△AOB=S△BOC,
∴S△AOB=S△BOC=S△DOC=S△AOD,
∴S△AOB=S ABCD,
∴S ABCD=8cm2.
故答案为:8cm2.
【点睛】
本题主要考查平行四边形的性质和等(同)底等高的三角形的面积相等,得出S△AOB=S ABCD是解题关键.
14.
【解析】
【分析】
不管P点在l上哪个位置,PD始终等于PD',故求PD'+PB可以转化成求PD+PB,显然当D、P、D'共线时PD+ PB最短.
【详解】
过点D作DM⊥AB交BA的延长线于点M,
∵四边形ABCD是平行四边形,AD=1,AB=2,∠ADC=60°,
∴∠DAM=60°,
由翻折变换可得,AD=AD′=1,DE=D′E,∠ADC=∠AD′E=60°,
∴∠DAM=∠AD′E=60°,∴AD∥D′E,
又∵DE∥AB,∴四边形ADED′是菱形,
∴点D与点D′关于直线l对称,
连接BD交直线l于点P,此时PD′+PB最小,PD′+PB=BD,
在Rt△DAM中,AD=1,∠DAM=60°,
∴AM=12AD=12,DM=32AD=32,
在Rt△DBM中,DM=32,MB=AB+AM=52,
∴BD=DM2+MB2=322+522=7,
即PD′+PB最小值为,
故答案为:.
【点睛】
本题考查平行四边形性质和菱形性质,掌握这些是本题解题关键.
15.18
【解析】
【分析】
根据平行四边形的性质得到AD∥BC,由平行线的性质得到∠AEG=∠EGF,根据折叠的性质得到∠GEF=∠DEF=60°,推出△EGF是等边三角形,于是得到结论.
【详解】
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEG=∠EGF,
∵将四边形EFCD沿EF翻折,得到四边形EFC′D′,
∴∠GEF=∠DEF=60°,
∴∠AEG=60°,
∴∠EGF=60°,
∴△EGF是等边三角形,
∵EF=6,
∴△GEF的周长=18,
故答案为18.
【点睛】
本题考查了翻折变换的性质、平行四边形的性质、等边三角形的判定,熟练掌握翻折变换的性质是解决问题的关键.
16.
【解析】
【分析】
根据平行四边形的性质:平行四边形的对角线互相平分.得两条对角线的一半分别是5,8;再根据三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边.进行求解.
【详解】
根据平行四边形的性质,得对角线的一半分别是5和8.
再根据三角形的三边关系,得.
故答案为.
【点睛】
本题考查了三角形的三边关系,掌握任意两边之和大于第三边,任意两边之差小于第三边是解题的关键.
17.44
【解析】
【分析】
先利用平行四边形的性质得到∠B=∠CDE=68°,再根据圆内接四边形的性质计算出∠ADC=112°,然后计算∠ADC﹣∠CDE即可.
【详解】
解:∵四边形BCDE为平行四边形,
∴∠B=∠CDE=68°,
∵四边形ABCD为圆的内接四边形,
∴∠B+∠ADC=180°,
∴∠ADC=180°﹣68°=112°,
∴∠ADE=∠ADC﹣∠CDE=112°﹣68°=44°.
故答案为44.
【点睛】
本题主要考查圆内接四边形的性质及平行四边形的性质,熟练掌握这两个性质定理是解题的关键.
18.
【解析】
【分析】
由作法得MN垂直平分AB,则AD=BD,延长ED到H点,使DH=DE,连接BH,FH,如图,证明△BDH≌△ADE得到BH=AE=3,∠DBH=∠A,再证明∠FBH=90°,则利用勾股定理计算出FH=3,然后证明DF垂直平分EH,从而得到EF=FH=3.
【详解】
由作法得MN垂直平分AB,
∴AD=BD,
延长ED到H点,使DH=DE,连接BH,FH,如图,
在△BDH和△ADE中,
,
∴△BDH≌△ADE(SAS),
∴BH=AE=3,∠DBH=∠A,
∵∠C=90°,
∴∠A+∠CBA=90°,
∴∠CBA+∠DBH=90°,
即∠FBH=90°,
在Rt△BHF中,FH3,
∵∠EDF=90°,
∴FD⊥EH,
而DH=DE,
即DF垂直平分EH,
∴EF=FH=3.
故答案为:3.
【点睛】
本题考查了作图﹣基本作图:熟练掌握5种基本作图是解决问题的关键.也考查了线段垂直平分线的性质全等三角形的判定以及性质,勾股定理.
19.1
【解析】
【分析】
由题意易得BM=MC,则有MN∥CD,,进而可求解.
【详解】
解: AB=AC,,
BM=MC,
BN=ND,
MN∥CD,,
AB=3,AD=5,
CD=2,
MN=1;
故答案为1.
【点睛】
本题主要考查等腰三角形的性质及三角形中位线,熟练掌握等腰三角形的性质及三角形中位线是解题的关键.
20.4.6
【解析】
【分析】
在AB上截取BF=AD,连接CF,通过证明△ADC≌△BFC,可得∠ACD=∠BCF,CD=CF,由“SAS”可得△DCE≌△FCE,可得DE=EF,即可求得结果.
【详解】
解:如图,在AB上截取BF=AD,连接CF,
∵CA=CB,∠ACB=120°,
∴∠CAB=∠CBA=30°,
∵∠DAE=60°
∴∠DAC=∠DAE﹣∠CAB=30°
∴∠DAC=∠CBA,且AD=BF,AC=BC
∴△ADC≌△BFC(SAS)
∴∠ACD=∠BCF,CD=CF,
∵∠ACB=∠ACE+∠ECF+∠BCF=∠ACE+∠ECF+∠ACD=∠DCE+∠ECF=120°
∴∠ECF=60°=∠DCE,且CE=CE,DC=CF
∴△DCE≌△FCE(SAS)
∴DE=EF
∴DE=BE﹣BF=BE﹣AD=7﹣2.4=4.6,
故答案为4.6
【点睛】
本题考查了全等三角形的判定和性质,等腰三角形的性质,添加恰当的辅助线构造全等三角形是本题的关键.
21.答案见解析
【解析】
【分析】
第一种:可画为平行四边形EFGH,第二种:可画为平行四边形DEBG.
【详解】
如图所示
【点睛】
此题考查了平行四边形的判定和学生的动手操作能力,解题的关键是熟知平行四边形的性质.
22.(1)
(2)9
【解析】
【分析】
(1)证明△ABD∽△CBA,根据相似三角形的性质求出BC,根据平行四边形的性质解答即可;
(2)分别延长EF,DC相交于点G,证明△EDF∽△EGD,求出EG,再证明四边形AEGC为平行四边形,得到AC=EG=18,根据正方形的性质计算即可.
(1)
解:∵∠BAD=∠C,∠ABD=∠CBA,
∴△ABD∽△CBA,
∴ ,
∴ ,
解得BC=.
∵ 四边形BCEF为平行四边形,
∴ EF=BC=.
(2)
解:如图④,分别延长EF,DC相交于点G,
∵ 四边形ABCD是正方形,
∴∠ACD=45°,AC=AD,
∵ EFAC,
∴∠EGD=∠ACD=45°,
∵∠EDF=45°,
∴∠EDF=∠EGD,
∵∠DEF=∠GED,
∴ △EDF∽△EGD,
∴
即,
解得EG=18,
∵ACEG,ABCD,
∴四边形AEGC为平行四边形,
∴AC=EG=18,
∴ AD=×18=9.
【点睛】
本题考查的是相似三角形的判定和性质、正方形的性质、平行四边形的判定和性质、,掌握相似三角形的判定定理和性质定理是解题的关键.
23.△MON≌△EOD,证明见解析
【解析】
【分析】
因为M、N分别为AB、AC边上的中点,∠A=∠A,可证明△AMN∽△ABC,则MN∥BC,又因为DE=BD+EC,证明 所以有△MON≌△EOD.
【详解】
解:△MON≌△EOD.
证明:∵M、N分别为AB、AC边上的中点,
∴AM∶AB=1∶2,AN∶AC=1∶2.
∵∠A=∠A,
∴△AMN∽△ABC.
∴∠AMN=∠ABC,MN=BC.
∴MN∥BC.
∴∠OMN=∠OED,∠ONM=∠ODE.
∵DE=BD+EC,
∴DE=BC.
∴MN=DE.
∴△MON≌△EOD.
【点睛】
本题考查的是三角形全等的判定,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.同时考查三角形相似的判定与性质,三角形的中位线的性质,知识的系统化是解题的关键.
24.
【解析】
【分析】
根据角平分线定义和直角三角形的两锐角互余求得∠MAC=30°,∠ABC=30°,再根据直角三角形中30°所对的直角边是斜边的一半和勾股定理分别求得MC、AC、AB、BC即可.
【详解】
解:∵AM是∠BAC的平分线,∠BAC=60°,∠C=90°,
∴∠MAC=30°,∠ABC=30°,
∴MC=AM=7.5cm,
∴AC=(cm),
∴AB=2AC=15(cm),
∴BC=(cm).
【点睛】
本题考查角平分线的定义、含30°角的直角三角形的性质、勾股定理,熟知含30°角的直角三角形的性质是解答的关键.
25.证明过程见详解.
【解析】
【分析】
先证四边形OCED是平行四边形,再由菱形的性质得∠DOC=90°,即可得出结论.
【详解】
证明:∵CE∥OD,DE∥OC,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴平行四边形OCED是矩形.
【点睛】
本题考查了菱形的性质、矩形的判定、平行四边形的判定与性质;熟练掌握矩形的判定和菱形的性质是解题的关键.
26.(1)OE=OF,(2)OE=OF,见解析
【解析】
【分析】
(1)根据正方形的性质及AM⊥DE,根据同角的余角相等,可知∠AFO=∠MEA,继而证明△AOF≌△DOE即可;
(2)方法同(1)解答即可;
【详解】
解:(1)∵正方形ABCD的对角线AC、BD相交于点O,AM⊥DE,
∴∠AOD=∠DOE=∠AME=90°,OA=OD,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠AFO=∠MEA,
在△AOF和△DOE中,
∴△AOF≌△DOE(ASA),
∴OE=OF,
故答案为:OE=OF;
(2)OE=OF,
理由如下:
∵正方形ABCD的对角线AC、BD相交于点O,AM⊥DE,
∴∠AOD=∠DOE=∠AME=90°,OA=OD,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠AFO=∠MEA,
在△AOF和△DOE中,
,
∴△AOF≌△DOE(ASA),
∴OE=OF.
【点睛】
本题考查了正方形的性质,三角形全等的判定与性质,熟悉以上性质与判定是解题的关键.
27..
【解析】
【分析】
证明△PBC∽△RBE,由相似三角形的性质得出,则BP=PR,得出 ,则QR=2PQ,可得出答案.
【详解】
解:∵ACDE,
∴△PBC∽△RBE,
∴,
∴BP=PR,
又∵△PCQ∽△RDQ,
∴,
∴QR=2PQ,
∴BP:PQ:QR=3:1:2.
【点睛】
此题考查了相似三角形的判定与性质以及平行四边形的性质.熟练掌握相似三角形的判定与性质是解题的关键.
一、单选题
1.内角和与外角和相等的图形是( )
A.三角形 B.四边形 C.五边形 D.六边形
2.判断下列命题正确的是( )
A.两条直线被第三条直线所截,同旁内角互补 B.三角形的三条高都在三角形的内部
C.平移前后图形的形状和大小都没有发生改变 D.过一点有且只有一条直线与已知直线平行
3.如图是平行四边形的边延长线上的一点,交于点,下列各式中错误的是( ).
A. B. C. D.
4.若一个正多边形的每个内角度数都为135°,则这个正多边形的边数是( )
A.6 B.8 C.10 D.12
5.已知∠AOB=100°,过点O作射线OC、OM,使∠AOC=20°,OM是∠BOC的平分线,则∠BOM的度数为( )
A.60° B.60°或40° C.120°或80° D.40°
6.在平面直角坐标系中,A,B,C三点的坐标分别为(0,0),(0,-5),(-2,-2),以这三点为平行四边形的三个顶点,则第四个顶点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如图,在平行四边形ABCD中,已知AD=6cm,AB=4cm,则平行四边形ABCD的周长为( )
A.6cm B.10cm C.12cm D.20cm
8.如图,D,E分别是△ABC的边AB,AC的中点,H,G是边BC上的点,且HG=BC,S△ABC=24,则图中阴影部分的面积为( )
A.4 B.6 C.8 D.12
9.下列命题是假命题的是( )
A.平行四边形的对角线互相平分 B.矩形的对角线互相垂直
C.菱形的对角线互相垂直平分 D.正方形的对角线互相垂直平分且相等
10.如图,平行四边形ABCD的对角线AC,BD相交于点O,CE平分交BD于点F,且,,连接OE,下列结论:①;②;③.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
二、填空题
11.如果一个多边形的每个外角都是40°,那么这个多边形是________边形.
12.如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=9cm,DE=4cm,求CE的长为__cm.
13. ABCD的对角线交于点O,S△AOB=2cm2,则S ABCD=________.
14.如图,平行四边形ABCD中,AB=2,AD=1,∠ADC=60°,将平行四边形ABCD沿过点A的直线l折叠,使点D落到AB边上的点处,折痕交CD边于点E.若点P是直线l上的一个动点,则+PB的最小值_______.
15.如图,E,F分别是 ABCD的边AD,BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折得到EFC′D′,ED′交BC于点C,则△GEF的周长为_____.
16.平行四边形的对角线长分别是、,则它的边长的取值范围是__________.
17.如图, BCDE的顶点B、C、D在半圆O上,顶点E在直径AB上,连接AD,若∠CDE=68°,则∠ADE的度数为_____°.
18.如图,在Rt△ABC中,∠C=90°,分别以A,B为圆心,大于的长为半径画弧,两弧交于点M,N,作直线MN交AB于点D,点E,F分别在边AC,BC上,连接EF.若∠EDF=90°,AE=3,BF=6,则线段EF的长为 _____.
19.如图,在ABC中,AB=AC,,延长AC到点D,连接BD,取BD的中点N,连接MN.若AB=3,AD=5,则MN=_______________.
20.如图,在△ABC中,CA=CB,∠ACB=120°,E为AB上一点,∠DCE=∠DAE=60°,AD=2.4,BE=7,则DE=_____.
三、解答题
21.如图所示,在中,两条对角线相交于点,点、、、分别是、、、的中点,以图中的任意四点(即点、、、、、、、、中的任意四点)为顶点画两种不同的平行四边形.
22.【阅读理解】我们知道,利用相似三角形性质求线段长是常用求线段长的方法之一,如图①,在△ABC中,D为BC上一点,若∠BAD=∠C,可易证△ABD∽△CBA,从而可得AB2=BD·BC,若已知其中两条线段的长即可求出第三条线段的长.
(1)【尝试应用】如图②,在 BCEF中,D为BC上一点,E为AC上一点,∠BAD=∠C,若AB=8,BD=5,求EF的长.
(2)【拓展应用】如图③,在正方形ABCD中,E是AB上一点,F是△ABC内一点,EFAC,∠EDF=45°,EF=8,DE=12,请求出正方形ABCD的边长.
23.如图,在△ABC中,M、N分别为AB、AC边上的中点.D、E为BC边上的两点,且DE=BD+EC,ME与ND交于点O,请你写出图中一对全等的三角形,并加以证明.
24.如图,在Rt△ABC中,∠C=90°,∠BAC=60°,AM平分∠BAC,AM的长为15cm,求BC的长.
25.已知:菱形ABCD的对角线AC,BD交于点O,CE∥OD,DE∥OC.求证:四边形OCED是矩形.
26.如图(1),正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接DE,过点A作AM⊥DE,垂足为M,AM与BD相交于点F.
(1)直接写出OE与OF的数量关系: ;
(2)如图(2)若点E在AC的延长线上,AM⊥DE于点M,AM交BD的延长线于点F,其他条件不变.试探究OE与OF的数量关系,并说明理由.
27.如图,四边形和四边形都是平行四边形,点R为的中点,分别交和于点P,Q,求.
参考答案:
1.B
【解析】
【分析】
设多边形有n条边,则内角和为180°(n-2),再根据内角和等于外角和可得方程180°(n-2)=360°,再解方程即可.
【详解】
解:设多边形有n条边,由题意得:
180°(n-2)=360°
解得:n=4,
故选:B.
【点睛】
此题主要考查了多边形的内角和和外角和,关键是掌握内角和为180°(n-2).
2.C
【解析】
【分析】
利用平移的性质以及三角形的高和平行线的性质分别进行判断即可.
【详解】
解:A、根据两条平行直线被第三条直线所截,同旁内角互补,故此选项错误;
B、钝角三角形的高可以在三角形的外部,故此选项错误;
C、根据平移的性质,平移前后图形的形状和大小都没有发生改变,故此选项正确;
D、过直线外一点有且只有一条直线与已知直线平行,故此选项错误.
故选:C.
【点睛】
此题主要考查了命题与定理,熟练利用相关定理与性质判断是解题关键.
3.D
【解析】
【分析】
根据平行四边形的性质和相似三角形的性质,逐一判断各个选项,即可.
【详解】
解:∵在平行四边形中,AD∥BC,
∴,A选项正确,不符合题意;
∵CD∥BE,
∴△CDF∽△EAF,
∴,
∵AB=CD,
∴,C选项正确,不符合题意;
∵CD∥BE,
∴∠E=∠FCD,
又∵∠B=∠D,
∴△CDF∽△EBC,
∴,B选项正确,不符合题意;
∵AD∥BC,
∴△AEF∽△EBC,
∴,
∴D错误.
故选:D.
【点睛】
此题主要考查了平行四边形、相似三角形的性质,熟练掌握相似三角形的判定和性质,是解题的关键.
4.B
【解析】
【分析】
根据题意可先求出这个正多边形的每个外角度数,再根据多边形的外角和是360°即可求出答案.
【详解】
解:因为一个正多边形的每个内角度数都为135°,
所以这个正多边形的每个外角度数都为45°,
所以这个正多边形的边数是360°÷45°=8.
故选:B.
【点睛】
本题考查了正多边形的有关概念和多边形的外角和,属于基本题目,熟练掌握多边形的基本知识是解题的关键.
5.B
【解析】
【分析】
分两种情况求解:①当OC在∠AOB内部时,②当OC在∠AOB外部时;分别求出∠BOM的度数即可.
【详解】
解:如图1,当OC在∠AOB内部时,
∵∠AOB=100°,∠AOC=20°,
∴∠BOC=80°,
∵OM是∠BOC的平分线,
∴∠BOM=40°;
如图,当OC在∠AOB外部时,
∵∠AOB=100°,∠AOC=20°,
∴∠BOC=120°,
∵OM是∠BOC的平分线,
∴∠BOM=60°;
综上所述:∠BOM的度数为40°或60°,
故选:B.
【点睛】
本题考察了角的计算,熟练掌握角平分线的性质,分两种情况画出图形是解题的关键.
6.A
【解析】
【分析】
已知线段AB,BC,AC,分别以三条线段为平行四边形的对角线,进行分类讨论,结合图形进行判断.
【详解】
如果以线段AB为对角线,AC,BC为边,作平行四边形,则第四个顶点在第四象限;
如果以线段AC为对角线,AB,BC为边,作平行四边形,则第四个顶点在第二象限;
如果以线段CB为对角线,AC,BA为边,作平行四边形,则第四个顶点在第三象限.
故不可能在第一象限.
故选A.
【点睛】
考查了平行四边形的性质,建立平面直角坐标系,数形结合,分类讨论是解题的关键.
7.D
【解析】
【分析】
根据平行四边形的性质:两组对边分别相等,即可求出周长.
【详解】
∵四边形ABCD是平行四边形,
∴BC=AD=6cm,CD=AB=4cm,
∴平行四边形ABCD的周长为(6+4)×2=20(cm),
故选:D.
【点睛】
本题考查了平行四边形的性质,熟练掌握平行四边形的性质是解答的关键.
8.D
【解析】
【分析】
连接DE,作AF⊥BC于F,根据三角形中位线定理得出DE=BC,DE∥BC,根据相似三角形的判定定理和性质定理,结合三角形面积计算即可.
【详解】
解:连接DE,作AF⊥BC于F,如图所示:
∵D,E分别是AB,AC的中点,
∴DE=BC,DE∥BC,AH=FH,
∴△ADE∽△ABC,AH⊥DE,
∴△ADE的面积=24×=6,
∴四边形DBCE的面积=24﹣6=18,
∵HG=BC,
∴DE=HG,
∴△DOE的面积+△HOG的面积=2×DE×AH=△ADE的面积=6,
∴图中阴影部分的面积=18﹣6=12,
故选D.
【点睛】
本题考查的是三角形中位线定理、相似三角形的判定和性质,掌握三角形的中位线定理,证明三角形相似是解题的关键.
9.B
【解析】
【分析】
利用平行四边形、矩形、菱形、正方形的性质解题即可.
【详解】
解:A、正确,平行四边形的对角线互相平分,故选项不符合;
B、错误,应该是矩形的对角线相等且互相平分,故选项符合;
C、正确,菱形的对角线互相垂直且平分,故选项不符合;
D、正确,正方形的对角线相等且互相垂直平分,故选项不符合;
故选:B.
【点睛】
本题考查命题与定理、特殊四边形的性质等知识,解题的关键是熟练掌握特殊四边形的性质,属于中考常考题型.
10.C
【解析】
【分析】
由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据角平分线的定义得到∠DCE=∠BCE=60°推出△CBE是等边三角形,证得∠ACB=90°,求出∠ACD=∠CAB=30°,故①正确;由AC⊥BC,得到S ABCD=AC BC,故②正确,根据直角三角形的性质得到,根据三角形的中位线的性质得到OE=BC,于是得到OE:AC=∶6;故③错误;
【详解】
解:∵四边形ABCD是平行四边形,
,
∵CE平分交AB于点E,
∴,
∴是等边三角形,
∴.
∵,
∴,
∴,
∴,故①正确;
∵,
∴,故②正确;
在中,,,
∴.
,,
∴,
,故③错误.
故选:C.
【点睛】
此题考查了平行四边形的性质、三角形中位线的性质以及等边三角形的判定与性质.注意证得△BCE是等边三角形,OE是△ABC的中位线是关键.
11.九
【解析】
【分析】
根据多边形的外角和是360度即可求得外角的个数,即多边形的边数.
【详解】
解:多边形的边数是:,
故答案为:九.
【点睛】
本题主要考查了多边形的外角和定理,理解多边形外角和中外角的个数与正多边形的边数之间的关系,是解题关键.
12.5.
【解析】
【分析】
根据角平分线和平行线的性质可证BD=FD,EF=CE,再根据线段和差可求CE的长.
【详解】
解:∵BF、CF分别平分∠ABC、∠ACG,
∴∠DBF=∠CBF,∠FCE=∠FCG,
∵DE∥BC,
∴∠DFB=∠CBF,∠EFC=∠FCG,
∴∠DBF=∠DFB,∠FCE=∠EFC,
∴BD=FD,EF=CE,
∵BD=9cm,DE=4cm,,
∴EF=DF﹣DE=BD﹣DE=9﹣4=5(cm),
∴EC=5cm,
故答案为:5.
【点睛】
本题考查了平行线的性质、角平分线的定义和等腰三角形的判定,解题关键是理解已知条件,根据角平分线和平行线得出等腰三角形.
13.
【解析】
【分析】
因为平行四边形的对角线互相平分,所以对角线分成的四个三角形的面积相等,即可得出答案.
【详解】
解:如图所示:∵四边形ABCD是平行四边形,
∴S△ABC=S△ADC,△AOB≌△DOC,△AOD≌△BOC,
∴S△AOB=S△DOC,S△AOD=S△BOC,
∵OA=OC,
∴S△AOB=S△BOC,
∴S△AOB=S△BOC=S△DOC=S△AOD,
∴S△AOB=S ABCD,
∴S ABCD=8cm2.
故答案为:8cm2.
【点睛】
本题主要考查平行四边形的性质和等(同)底等高的三角形的面积相等,得出S△AOB=S ABCD是解题关键.
14.
【解析】
【分析】
不管P点在l上哪个位置,PD始终等于PD',故求PD'+PB可以转化成求PD+PB,显然当D、P、D'共线时PD+ PB最短.
【详解】
过点D作DM⊥AB交BA的延长线于点M,
∵四边形ABCD是平行四边形,AD=1,AB=2,∠ADC=60°,
∴∠DAM=60°,
由翻折变换可得,AD=AD′=1,DE=D′E,∠ADC=∠AD′E=60°,
∴∠DAM=∠AD′E=60°,∴AD∥D′E,
又∵DE∥AB,∴四边形ADED′是菱形,
∴点D与点D′关于直线l对称,
连接BD交直线l于点P,此时PD′+PB最小,PD′+PB=BD,
在Rt△DAM中,AD=1,∠DAM=60°,
∴AM=12AD=12,DM=32AD=32,
在Rt△DBM中,DM=32,MB=AB+AM=52,
∴BD=DM2+MB2=322+522=7,
即PD′+PB最小值为,
故答案为:.
【点睛】
本题考查平行四边形性质和菱形性质,掌握这些是本题解题关键.
15.18
【解析】
【分析】
根据平行四边形的性质得到AD∥BC,由平行线的性质得到∠AEG=∠EGF,根据折叠的性质得到∠GEF=∠DEF=60°,推出△EGF是等边三角形,于是得到结论.
【详解】
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEG=∠EGF,
∵将四边形EFCD沿EF翻折,得到四边形EFC′D′,
∴∠GEF=∠DEF=60°,
∴∠AEG=60°,
∴∠EGF=60°,
∴△EGF是等边三角形,
∵EF=6,
∴△GEF的周长=18,
故答案为18.
【点睛】
本题考查了翻折变换的性质、平行四边形的性质、等边三角形的判定,熟练掌握翻折变换的性质是解决问题的关键.
16.
【解析】
【分析】
根据平行四边形的性质:平行四边形的对角线互相平分.得两条对角线的一半分别是5,8;再根据三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边.进行求解.
【详解】
根据平行四边形的性质,得对角线的一半分别是5和8.
再根据三角形的三边关系,得.
故答案为.
【点睛】
本题考查了三角形的三边关系,掌握任意两边之和大于第三边,任意两边之差小于第三边是解题的关键.
17.44
【解析】
【分析】
先利用平行四边形的性质得到∠B=∠CDE=68°,再根据圆内接四边形的性质计算出∠ADC=112°,然后计算∠ADC﹣∠CDE即可.
【详解】
解:∵四边形BCDE为平行四边形,
∴∠B=∠CDE=68°,
∵四边形ABCD为圆的内接四边形,
∴∠B+∠ADC=180°,
∴∠ADC=180°﹣68°=112°,
∴∠ADE=∠ADC﹣∠CDE=112°﹣68°=44°.
故答案为44.
【点睛】
本题主要考查圆内接四边形的性质及平行四边形的性质,熟练掌握这两个性质定理是解题的关键.
18.
【解析】
【分析】
由作法得MN垂直平分AB,则AD=BD,延长ED到H点,使DH=DE,连接BH,FH,如图,证明△BDH≌△ADE得到BH=AE=3,∠DBH=∠A,再证明∠FBH=90°,则利用勾股定理计算出FH=3,然后证明DF垂直平分EH,从而得到EF=FH=3.
【详解】
由作法得MN垂直平分AB,
∴AD=BD,
延长ED到H点,使DH=DE,连接BH,FH,如图,
在△BDH和△ADE中,
,
∴△BDH≌△ADE(SAS),
∴BH=AE=3,∠DBH=∠A,
∵∠C=90°,
∴∠A+∠CBA=90°,
∴∠CBA+∠DBH=90°,
即∠FBH=90°,
在Rt△BHF中,FH3,
∵∠EDF=90°,
∴FD⊥EH,
而DH=DE,
即DF垂直平分EH,
∴EF=FH=3.
故答案为:3.
【点睛】
本题考查了作图﹣基本作图:熟练掌握5种基本作图是解决问题的关键.也考查了线段垂直平分线的性质全等三角形的判定以及性质,勾股定理.
19.1
【解析】
【分析】
由题意易得BM=MC,则有MN∥CD,,进而可求解.
【详解】
解: AB=AC,,
BM=MC,
BN=ND,
MN∥CD,,
AB=3,AD=5,
CD=2,
MN=1;
故答案为1.
【点睛】
本题主要考查等腰三角形的性质及三角形中位线,熟练掌握等腰三角形的性质及三角形中位线是解题的关键.
20.4.6
【解析】
【分析】
在AB上截取BF=AD,连接CF,通过证明△ADC≌△BFC,可得∠ACD=∠BCF,CD=CF,由“SAS”可得△DCE≌△FCE,可得DE=EF,即可求得结果.
【详解】
解:如图,在AB上截取BF=AD,连接CF,
∵CA=CB,∠ACB=120°,
∴∠CAB=∠CBA=30°,
∵∠DAE=60°
∴∠DAC=∠DAE﹣∠CAB=30°
∴∠DAC=∠CBA,且AD=BF,AC=BC
∴△ADC≌△BFC(SAS)
∴∠ACD=∠BCF,CD=CF,
∵∠ACB=∠ACE+∠ECF+∠BCF=∠ACE+∠ECF+∠ACD=∠DCE+∠ECF=120°
∴∠ECF=60°=∠DCE,且CE=CE,DC=CF
∴△DCE≌△FCE(SAS)
∴DE=EF
∴DE=BE﹣BF=BE﹣AD=7﹣2.4=4.6,
故答案为4.6
【点睛】
本题考查了全等三角形的判定和性质,等腰三角形的性质,添加恰当的辅助线构造全等三角形是本题的关键.
21.答案见解析
【解析】
【分析】
第一种:可画为平行四边形EFGH,第二种:可画为平行四边形DEBG.
【详解】
如图所示
【点睛】
此题考查了平行四边形的判定和学生的动手操作能力,解题的关键是熟知平行四边形的性质.
22.(1)
(2)9
【解析】
【分析】
(1)证明△ABD∽△CBA,根据相似三角形的性质求出BC,根据平行四边形的性质解答即可;
(2)分别延长EF,DC相交于点G,证明△EDF∽△EGD,求出EG,再证明四边形AEGC为平行四边形,得到AC=EG=18,根据正方形的性质计算即可.
(1)
解:∵∠BAD=∠C,∠ABD=∠CBA,
∴△ABD∽△CBA,
∴ ,
∴ ,
解得BC=.
∵ 四边形BCEF为平行四边形,
∴ EF=BC=.
(2)
解:如图④,分别延长EF,DC相交于点G,
∵ 四边形ABCD是正方形,
∴∠ACD=45°,AC=AD,
∵ EFAC,
∴∠EGD=∠ACD=45°,
∵∠EDF=45°,
∴∠EDF=∠EGD,
∵∠DEF=∠GED,
∴ △EDF∽△EGD,
∴
即,
解得EG=18,
∵ACEG,ABCD,
∴四边形AEGC为平行四边形,
∴AC=EG=18,
∴ AD=×18=9.
【点睛】
本题考查的是相似三角形的判定和性质、正方形的性质、平行四边形的判定和性质、,掌握相似三角形的判定定理和性质定理是解题的关键.
23.△MON≌△EOD,证明见解析
【解析】
【分析】
因为M、N分别为AB、AC边上的中点,∠A=∠A,可证明△AMN∽△ABC,则MN∥BC,又因为DE=BD+EC,证明 所以有△MON≌△EOD.
【详解】
解:△MON≌△EOD.
证明:∵M、N分别为AB、AC边上的中点,
∴AM∶AB=1∶2,AN∶AC=1∶2.
∵∠A=∠A,
∴△AMN∽△ABC.
∴∠AMN=∠ABC,MN=BC.
∴MN∥BC.
∴∠OMN=∠OED,∠ONM=∠ODE.
∵DE=BD+EC,
∴DE=BC.
∴MN=DE.
∴△MON≌△EOD.
【点睛】
本题考查的是三角形全等的判定,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.同时考查三角形相似的判定与性质,三角形的中位线的性质,知识的系统化是解题的关键.
24.
【解析】
【分析】
根据角平分线定义和直角三角形的两锐角互余求得∠MAC=30°,∠ABC=30°,再根据直角三角形中30°所对的直角边是斜边的一半和勾股定理分别求得MC、AC、AB、BC即可.
【详解】
解:∵AM是∠BAC的平分线,∠BAC=60°,∠C=90°,
∴∠MAC=30°,∠ABC=30°,
∴MC=AM=7.5cm,
∴AC=(cm),
∴AB=2AC=15(cm),
∴BC=(cm).
【点睛】
本题考查角平分线的定义、含30°角的直角三角形的性质、勾股定理,熟知含30°角的直角三角形的性质是解答的关键.
25.证明过程见详解.
【解析】
【分析】
先证四边形OCED是平行四边形,再由菱形的性质得∠DOC=90°,即可得出结论.
【详解】
证明:∵CE∥OD,DE∥OC,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴平行四边形OCED是矩形.
【点睛】
本题考查了菱形的性质、矩形的判定、平行四边形的判定与性质;熟练掌握矩形的判定和菱形的性质是解题的关键.
26.(1)OE=OF,(2)OE=OF,见解析
【解析】
【分析】
(1)根据正方形的性质及AM⊥DE,根据同角的余角相等,可知∠AFO=∠MEA,继而证明△AOF≌△DOE即可;
(2)方法同(1)解答即可;
【详解】
解:(1)∵正方形ABCD的对角线AC、BD相交于点O,AM⊥DE,
∴∠AOD=∠DOE=∠AME=90°,OA=OD,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠AFO=∠MEA,
在△AOF和△DOE中,
∴△AOF≌△DOE(ASA),
∴OE=OF,
故答案为:OE=OF;
(2)OE=OF,
理由如下:
∵正方形ABCD的对角线AC、BD相交于点O,AM⊥DE,
∴∠AOD=∠DOE=∠AME=90°,OA=OD,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠AFO=∠MEA,
在△AOF和△DOE中,
,
∴△AOF≌△DOE(ASA),
∴OE=OF.
【点睛】
本题考查了正方形的性质,三角形全等的判定与性质,熟悉以上性质与判定是解题的关键.
27..
【解析】
【分析】
证明△PBC∽△RBE,由相似三角形的性质得出,则BP=PR,得出 ,则QR=2PQ,可得出答案.
【详解】
解:∵ACDE,
∴△PBC∽△RBE,
∴,
∴BP=PR,
又∵△PCQ∽△RDQ,
∴,
∴QR=2PQ,
∴BP:PQ:QR=3:1:2.
【点睛】
此题考查了相似三角形的判定与性质以及平行四边形的性质.熟练掌握相似三角形的判定与性质是解题的关键.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
