6.4.3.3余弦定理、正弦定理的应用举例课件-2021-2022学年高一下学期数学人教A版(2019)必修第二册(共13张PPT)
文档属性
| 名称 | 6.4.3.3余弦定理、正弦定理的应用举例课件-2021-2022学年高一下学期数学人教A版(2019)必修第二册(共13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 525.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-23 22:04:38 | ||
图片预览




文档简介
(共13张PPT)
6.4.3.3 正余弦定理的应用举例
仰角:当视线在水平线上方时,视线与水平线所成角。
俯角:当视线在水平线下方时,视线与水平线所成角。
水平线
视线
视线
仰角
俯角
1.仰角、俯角
东
西
北
南
600
300
450
200
A
B
C
D
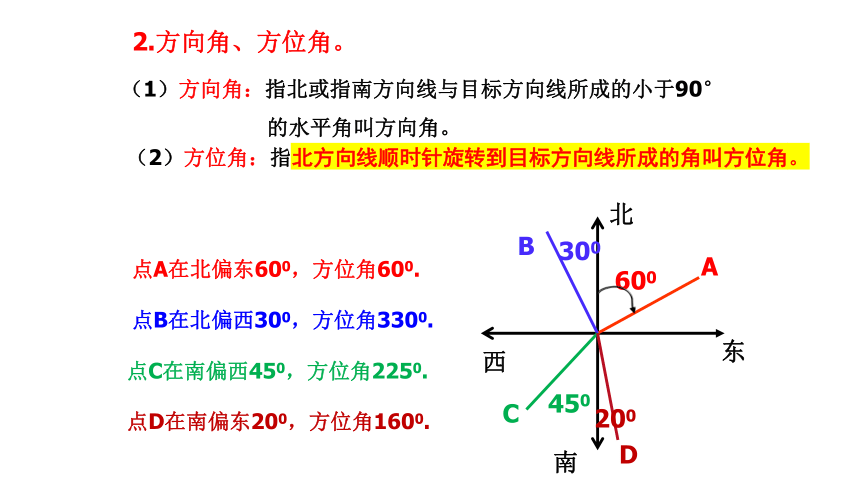
点A在北偏东600,方位角600.
点B在北偏西300,方位角3300.
点C在南偏西450,方位角2250.
点D在南偏东200,方位角1600.
(1)方向角:指北或指南方向线与目标方向线所成的小于90°
的水平角叫方向角。
(2)方位角:指北方向线顺时针旋转到目标方向线所成的角叫方位角。
2.方向角、方位角。
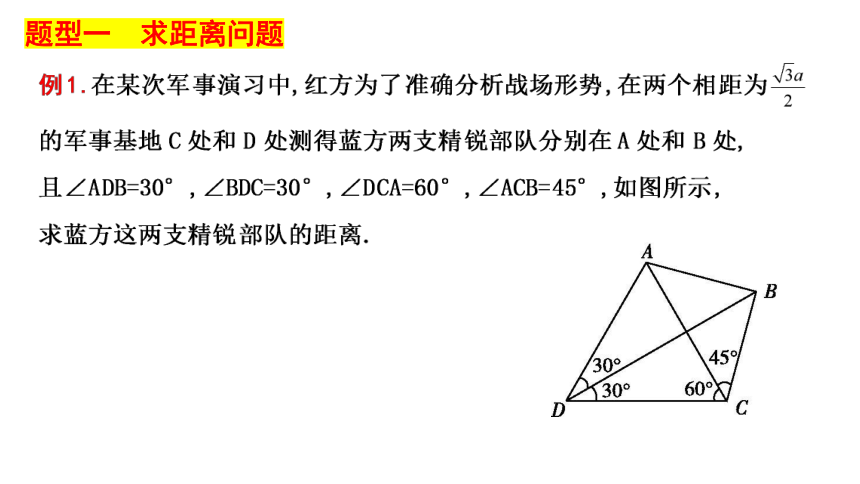
题型一 求距离问题
方法技巧
求距离问题的注意事项:
(1)选定或确定所求量所在的三角形.若其他量已知,则直接求解;
若有未知量,则把未知量放在另一三角形中求解.
(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理.
练习一:
题型二 求高度问题
例2.如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北15°的方向上,行驶5 km后到达B处,测得此山顶在西偏北25°的方向上,仰角为8°,求此山的高CD(精确到1 m).
解:在△ABC中,∠A=15°,∠C= 25°-15°=10°.
在Rt△DCB中CD=BC×tan∠DBC≈BC×tan8°≈1047(m).
答:山的高约为1047米.
(1)“空间”向“平面”的转化:
测量高度问题往往是空间中的问题,因此先要选好所求线段所在的平面,将空间问题转化为平面问题.
(2)“解直角三角形”与“解斜三角形”结合,全面分析所有三角形,仔细规划解题思路.
方法技巧 求高度问题的解题策略:
A
练习二:
题型三 测量角度问题
方法技巧
测量角度问题主要是指在海上或空中测量角度的问题,如确定目标的方位,观察某一建筑物的视角等.
解决它们的关键是根据题意和图形及有关概念,确定所求的角在哪个三角形中,该三角形中已知哪些量,需要求哪些量.通常是根据题意,从实际问题中抽象出一个或几个三角形,然后通过解这些三角形,得到所求的量,从而得到实际问题的解.
练习三:
练习三:
6.4.3.3 正余弦定理的应用举例
仰角:当视线在水平线上方时,视线与水平线所成角。
俯角:当视线在水平线下方时,视线与水平线所成角。
水平线
视线
视线
仰角
俯角
1.仰角、俯角
东
西
北
南
600
300
450
200
A
B
C
D
点A在北偏东600,方位角600.
点B在北偏西300,方位角3300.
点C在南偏西450,方位角2250.
点D在南偏东200,方位角1600.
(1)方向角:指北或指南方向线与目标方向线所成的小于90°
的水平角叫方向角。
(2)方位角:指北方向线顺时针旋转到目标方向线所成的角叫方位角。
2.方向角、方位角。
题型一 求距离问题
方法技巧
求距离问题的注意事项:
(1)选定或确定所求量所在的三角形.若其他量已知,则直接求解;
若有未知量,则把未知量放在另一三角形中求解.
(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理.
练习一:
题型二 求高度问题
例2.如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北15°的方向上,行驶5 km后到达B处,测得此山顶在西偏北25°的方向上,仰角为8°,求此山的高CD(精确到1 m).
解:在△ABC中,∠A=15°,∠C= 25°-15°=10°.
在Rt△DCB中CD=BC×tan∠DBC≈BC×tan8°≈1047(m).
答:山的高约为1047米.
(1)“空间”向“平面”的转化:
测量高度问题往往是空间中的问题,因此先要选好所求线段所在的平面,将空间问题转化为平面问题.
(2)“解直角三角形”与“解斜三角形”结合,全面分析所有三角形,仔细规划解题思路.
方法技巧 求高度问题的解题策略:
A
练习二:
题型三 测量角度问题
方法技巧
测量角度问题主要是指在海上或空中测量角度的问题,如确定目标的方位,观察某一建筑物的视角等.
解决它们的关键是根据题意和图形及有关概念,确定所求的角在哪个三角形中,该三角形中已知哪些量,需要求哪些量.通常是根据题意,从实际问题中抽象出一个或几个三角形,然后通过解这些三角形,得到所求的量,从而得到实际问题的解.
练习三:
练习三:
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
