2022年广东中考数学压轴解答题限时训练(共12张PPT)
文档属性
| 名称 | 2022年广东中考数学压轴解答题限时训练(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 534.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
限时训练
2022年广东中考压轴解答题限时训练(3)
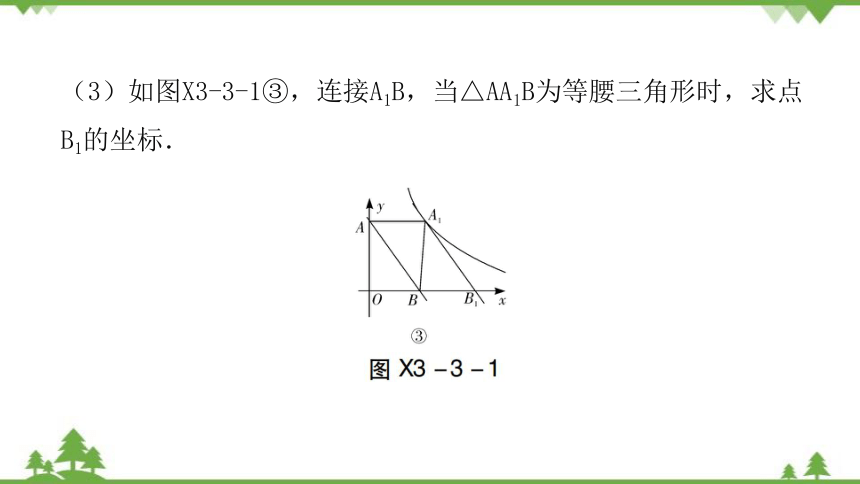
(3)如图X3-3-1③,连接A1B,当△AA1B为等腰三角形时,求点B1的坐标.
(2)∵A(0,4),B(3,0),点C为线段AB的中点,
∴
将直线AB向右平移m个单位长度,则A1(m,4),C1
且AA1∥BB1,AA1=BB1=m.∴四边形ABB1A1是平行四边形.
∵反比例函数的图象经过点C1,A1,∴4m=2×
即m=
∴四边形ABB1A1的面积为4× =6.
(3)∵A(0,4),B(3,0),∴OA=4,OB=3.
∴AB= =5.
∵四边形ABB1A1是平行四边形,
∴A1B1=AB=5,AA1=BB1=m.
①当AA1=AB时,即m=5.∴B1(8,0);
②当A1B=AA1时,即 =m.解得m=
∴B1
③当A1B=AB时,即 =5.解得m1=0(不合题意,舍去),m2=6.∴B1(9,0).
综上所述,点B1坐标为(8,0)或 或(9,0).
2. (12分)(无图题)在△ABC中,∠BAC=90°,AB=AC,点D为射线BC上一动点(点D不与点B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)画出图形,判断BC与CF的位置关系,说明理由;
(2)判断BC,CD,CF之间的数量关系,说明理由.
(2)BC,CD,CF之间的数量关系是BC=CF+CD或CF=BC+CD.理由如下:
①当点D在线段BC上时,
∵△DAB≌△FAC,∴CF=BD.
∵BC=BD+CD,∴BC=CF+CD;
②当点D在线段BC的延长线上时,
∵△ABD≌△ACF,∴CF=BD.
∵BD=BC+CD,∴CF=BC+CD.
谢 谢
限时训练
2022年广东中考压轴解答题限时训练(3)
(3)如图X3-3-1③,连接A1B,当△AA1B为等腰三角形时,求点B1的坐标.
(2)∵A(0,4),B(3,0),点C为线段AB的中点,
∴
将直线AB向右平移m个单位长度,则A1(m,4),C1
且AA1∥BB1,AA1=BB1=m.∴四边形ABB1A1是平行四边形.
∵反比例函数的图象经过点C1,A1,∴4m=2×
即m=
∴四边形ABB1A1的面积为4× =6.
(3)∵A(0,4),B(3,0),∴OA=4,OB=3.
∴AB= =5.
∵四边形ABB1A1是平行四边形,
∴A1B1=AB=5,AA1=BB1=m.
①当AA1=AB时,即m=5.∴B1(8,0);
②当A1B=AA1时,即 =m.解得m=
∴B1
③当A1B=AB时,即 =5.解得m1=0(不合题意,舍去),m2=6.∴B1(9,0).
综上所述,点B1坐标为(8,0)或 或(9,0).
2. (12分)(无图题)在△ABC中,∠BAC=90°,AB=AC,点D为射线BC上一动点(点D不与点B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)画出图形,判断BC与CF的位置关系,说明理由;
(2)判断BC,CD,CF之间的数量关系,说明理由.
(2)BC,CD,CF之间的数量关系是BC=CF+CD或CF=BC+CD.理由如下:
①当点D在线段BC上时,
∵△DAB≌△FAC,∴CF=BD.
∵BC=BD+CD,∴BC=CF+CD;
②当点D在线段BC的延长线上时,
∵△ABD≌△ACF,∴CF=BD.
∵BD=BC+CD,∴CF=BC+CD.
谢 谢
同课章节目录
