2022年高考考前20天终极冲刺攻略(二)核心考点解读—— 平面向量与复数
文档属性
| 名称 | 2022年高考考前20天终极冲刺攻略(二)核心考点解读—— 平面向量与复数 |  | |
| 格式 | doc | ||
| 文件大小 | 756.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-23 22:18:26 | ||
图片预览




文档简介
时间:5月 23 日 今日心情:
核心考点解读—— 平面向量与复数
高考预测 1.平面向量是高考考查的重点.热点.往往以选择题或填空题的形式出现.常以平面图形为载体,考查线性运算.数量积.夹角.垂直的条件等问题; 2.同三角函数.解析几何.不等式等知识相结合,考查数形结合思想.函数方程思想以及分析问题解决问题的能力.难度为中等或中等偏易.3.考查复数的概念.几何意义.复数的运算.常见题型有选择题.填空题,重点考查除法.乘法等运算,同时考查复数的模.共轭复数等概念.
应试技巧 一.平面向量1.共线向量基本定理(1)如果,则;反之,如果且,则一定存在唯一的实数,使.(2)平面向量共线的坐标表示若,,则的充要条件是,这与在本质上是没有差异的,只是形式上不同.2.平面向量基本定理:如果和是同一个平面内的两个不共线向量,那么对于该平面内的任一向量,都存在唯一的一对实数,使得,我们把不共线向量,叫做表示这一平面内所有向量的一组基底,记为.(简而言之,不共线的两个向量可以表示所有向量)3.向量数量积运算,其中为向量的夹角4.数量积运算法则:(1)交换律: (2)系数结合律:(3)分配律:5.平面向量数量积的重要性质(1);(2)非零向量,,;(3)当与同向时,;当与反向时,,,;(4);(5).8.平面向量数量积有关性质的坐标表示设向量,,则,由此得到(1)若,则或.(2)设,则A.B两点间的距离.(3)设两个非零向量,,,,则.(4)设是与的夹角,则二.复数1.基本概念(1)叫虚数单位,满足 ,当时,.(2)形如的数叫复数,记作.①复数与复平面上的点一一对应,叫z的实部,b叫z的虚部; Z点组成实轴;叫虚数;且,z叫纯虚数,纯虚数对应点组成虚轴(不包括原点)。两个实部相等,虚部互为相反数的复数互为共轭复数. ②两个复数相等(两复数对应同一点)③复数的模:复数的模,也就是向量的模,即有向线段的长度,其计算公式为,显然,.2.复数运算(1)(2)其中,叫z的模;是的共轭复数.(3).实数的全部运算律(加法和乘法的交换律.结合律.分配律及整数指数幂运算法则)都适用于复数.3.复数的几何意义(1)复数对应平面内的点;(2)复数对应平面向量;(3)复平面内实轴上的点表示实数,除原点外虚轴上的点表示虚数,各象限内的点都表示复数.(4)复数的模表示复平面内的点到原点的距离.
平面向量部分
1.(2021·浙江·高考真题)已知非零向量,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
【答案】B
【解析】
如图所示,,当时,与垂直,,所以成立,此时,
∴不是的充分条件,
当时,,∴,∴成立,
∴是的必要条件,
综上,“”是“”的必要不充分条件
故选:B.
2.(2020·山东·高考真题)已知平行四边形,点,分别是,的中点(如图所示),设,,则等于( )
A. B. C. D.
【答案】A
【解析】
连结,则为的中位线,
,
故选:A
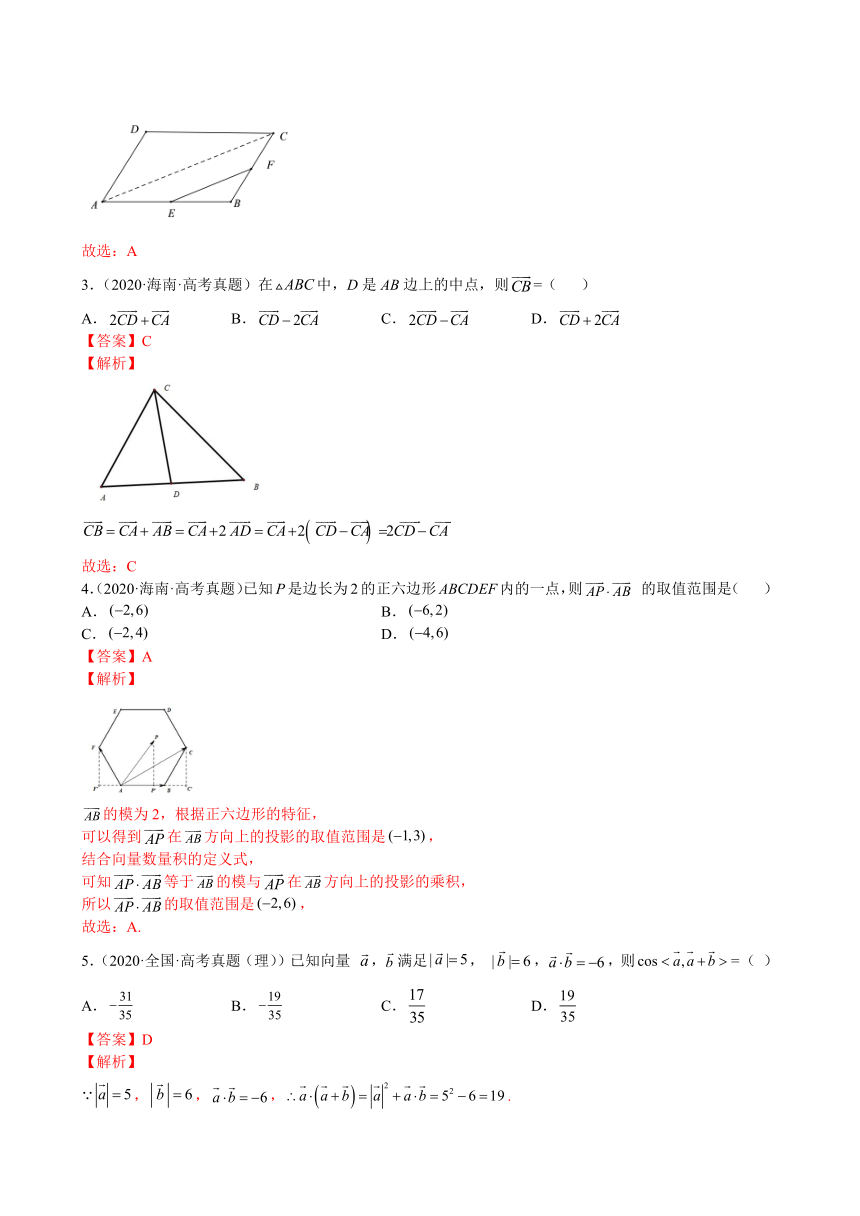
3.(2020·海南·高考真题)在中,D是AB边上的中点,则=( )
A. B. C. D.
【答案】C
【解析】
故选:C
4.(2020·海南·高考真题)已知P是边长为2的正六边形ABCDEF内的一点,则 的取值范围是( )
A. B.
C. D.
【答案】A
【解析】
的模为2,根据正六边形的特征,
可以得到在方向上的投影的取值范围是,
结合向量数量积的定义式,
可知等于的模与在方向上的投影的乘积,
所以的取值范围是,
故选:A.
5.(2020·全国·高考真题(理))已知向量 ,满足, ,,则( )
A. B. C. D.
【答案】D
【解析】
,,,.
,
因此,.
故选:D.
(多选题)6.(2021·全国·高考真题)已知为坐标原点,点,,,,则( )
A. B.
C. D.
【答案】AC
【解析】
【分析】
A.B写出,.,的坐标,利用坐标公式求模,即可判断正误;C.D根据向量的坐标,应用向量数量积的坐标表示及两角和差公式化简,即可判断正误.
【详解】
A:,,所以,,故,正确;
B:,,所以,同理,故不一定相等,错误;
C:由题意得:,,正确;
D:由题意得:,
,故一般来说故错误;
故选:AC
7.(2021·天津·高考真题)在边长为1的等边三角形ABC中,D为线段BC上的动点,且交AB于点E.且交AC于点F,则的值为____________;的最小值为____________.
【答案】 1
【解析】
设,,为边长为1的等边三角形,,
,
,为边长为的等边三角形,,
,
,
,
所以当时,的最小值为.
故答案为:1;.
8.(2020·天津·高考真题)如图,在四边形中,,,且,则实数的值为_________,若是线段上的动点,且,则的最小值为_________.
【答案】
【解析】
,,,
,
解得,
以点为坐标原点,所在直线为轴建立如下图所示的平面直角坐标系,
,
∵,∴的坐标为,
∵又∵,则,设,则(其中),
,,
,
所以,当时,取得最小值.
9.(2020·北京·高考真题)已知正方形的边长为2,点P满足,则_________;_________.
【答案】
【解析】
以点为坐标原点,.所在直线分别为.轴建立如下图所示的平面直角坐标系,
则点...,
,
则点,,,
因此,,.故答案为:;.
10.(2021·湖南·高考真题)已知向量,,则___________
【答案】
【解析】
,所以.故答案为:
11.(2021·全国·高考真题)已知向量,,,_______.
【答案】
【解析】
由已知可得,
因此,.故答案为:.
12.(2021·全国·高考真题(理))已知向量,若,则__________.
【答案】
【解析】因为,所以由可得,
,解得.故答案为:.
13.(2021·全国·高考真题(文))若向量满足,则_________.
【答案】
【解析】∵,∴
∴.故答案为:.
14.(2020·全国·高考真题(理))已知单位向量,的夹角为45°,与垂直,则k=__________.
【答案】
【解析】由题意可得:,
由向量垂直的充分必要条件可得:,
即:,解得:.
故答案为:.
复数部分
1.(2021·江苏·高考真题)若复数满足,则的虚部等于( )
A.4 B.2 C.-2 D.-4
【答案】C
【解析】若复数满足,则,
所以的虚部等于.故选:C.
2.(2021·全国·高考真题)复数在复平面内对应的点所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】A
【解析】,所以该复数对应的点为,
该点在第一象限,故选:A.
3.(2021·北京·高考真题)在复平面内,复数满足,则( )
A. B. C. D.
【答案】D
【解析】由题意可得:.故选:D.
4.(2021·全国·高考真题(文))已知,则( )
A. B. C. D.
【答案】B
【解析】,.故选:B.
5.(2021·全国·高考真题(理))设,则( )
A. B. C. D.
【答案】C
【解析】设,则,则,
所以,,解得,因此,.故选:C.
6.(2021·浙江·高考真题)已知,,(i为虚数单位),则( )
A. B.1 C. D.3
【答案】C
【解析】,
利用复数相等的充分必要条件可得:.故选:C.
7.(2020·北京·高考真题)在复平面内,复数对应的点的坐标是,则( ).
A. B. C. D.
【答案】B
【解析】由题意得,.故选:B.
8.(2020·浙江·高考真题)已知a∈R,若a–1+(a–2)i(i为虚数单位)是实数,则a=( )
A.1 B.–1 C.2 D.–2
【答案】C
【解析】因为为实数,所以,故选:C
9.(2020·全国·高考真题(文))(1–i)4=( )
A.–4 B.4
C.–4i D.4i
【答案】A
【解析】
.故选:A.
10.(2021·天津·高考真题)是虚数单位,复数_____________.
【答案】
【解析】.故答案为:.
11.(2020·天津·高考真题)是虚数单位,复数_________.
【答案】
【解析】
.
故答案为:.
12.(2020·江苏·高考真题)已知是虚数单位,则复数的实部是_____.
【答案】3
【解析】
∵复数
∴
∴复数的实部为3.
13.(2020·全国·高考真题(理))设复数,满足,,则=__________.
【答案】
【解析】方法一:设,,
,
,又,所以,,
.
故答案为:.
方法二:如图所示,设复数所对应的点为,,
由已知,
∴平行四边形为菱形,且都是正三角形,∴,
∴.
核心考点解读—— 平面向量与复数
高考预测 1.平面向量是高考考查的重点.热点.往往以选择题或填空题的形式出现.常以平面图形为载体,考查线性运算.数量积.夹角.垂直的条件等问题; 2.同三角函数.解析几何.不等式等知识相结合,考查数形结合思想.函数方程思想以及分析问题解决问题的能力.难度为中等或中等偏易.3.考查复数的概念.几何意义.复数的运算.常见题型有选择题.填空题,重点考查除法.乘法等运算,同时考查复数的模.共轭复数等概念.
应试技巧 一.平面向量1.共线向量基本定理(1)如果,则;反之,如果且,则一定存在唯一的实数,使.(2)平面向量共线的坐标表示若,,则的充要条件是,这与在本质上是没有差异的,只是形式上不同.2.平面向量基本定理:如果和是同一个平面内的两个不共线向量,那么对于该平面内的任一向量,都存在唯一的一对实数,使得,我们把不共线向量,叫做表示这一平面内所有向量的一组基底,记为.(简而言之,不共线的两个向量可以表示所有向量)3.向量数量积运算,其中为向量的夹角4.数量积运算法则:(1)交换律: (2)系数结合律:(3)分配律:5.平面向量数量积的重要性质(1);(2)非零向量,,;(3)当与同向时,;当与反向时,,,;(4);(5).8.平面向量数量积有关性质的坐标表示设向量,,则,由此得到(1)若,则或.(2)设,则A.B两点间的距离.(3)设两个非零向量,,,,则.(4)设是与的夹角,则二.复数1.基本概念(1)叫虚数单位,满足 ,当时,.(2)形如的数叫复数,记作.①复数与复平面上的点一一对应,叫z的实部,b叫z的虚部; Z点组成实轴;叫虚数;且,z叫纯虚数,纯虚数对应点组成虚轴(不包括原点)。两个实部相等,虚部互为相反数的复数互为共轭复数. ②两个复数相等(两复数对应同一点)③复数的模:复数的模,也就是向量的模,即有向线段的长度,其计算公式为,显然,.2.复数运算(1)(2)其中,叫z的模;是的共轭复数.(3).实数的全部运算律(加法和乘法的交换律.结合律.分配律及整数指数幂运算法则)都适用于复数.3.复数的几何意义(1)复数对应平面内的点;(2)复数对应平面向量;(3)复平面内实轴上的点表示实数,除原点外虚轴上的点表示虚数,各象限内的点都表示复数.(4)复数的模表示复平面内的点到原点的距离.
平面向量部分
1.(2021·浙江·高考真题)已知非零向量,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
【答案】B
【解析】
如图所示,,当时,与垂直,,所以成立,此时,
∴不是的充分条件,
当时,,∴,∴成立,
∴是的必要条件,
综上,“”是“”的必要不充分条件
故选:B.
2.(2020·山东·高考真题)已知平行四边形,点,分别是,的中点(如图所示),设,,则等于( )
A. B. C. D.
【答案】A
【解析】
连结,则为的中位线,
,
故选:A
3.(2020·海南·高考真题)在中,D是AB边上的中点,则=( )
A. B. C. D.
【答案】C
【解析】
故选:C
4.(2020·海南·高考真题)已知P是边长为2的正六边形ABCDEF内的一点,则 的取值范围是( )
A. B.
C. D.
【答案】A
【解析】
的模为2,根据正六边形的特征,
可以得到在方向上的投影的取值范围是,
结合向量数量积的定义式,
可知等于的模与在方向上的投影的乘积,
所以的取值范围是,
故选:A.
5.(2020·全国·高考真题(理))已知向量 ,满足, ,,则( )
A. B. C. D.
【答案】D
【解析】
,,,.
,
因此,.
故选:D.
(多选题)6.(2021·全国·高考真题)已知为坐标原点,点,,,,则( )
A. B.
C. D.
【答案】AC
【解析】
【分析】
A.B写出,.,的坐标,利用坐标公式求模,即可判断正误;C.D根据向量的坐标,应用向量数量积的坐标表示及两角和差公式化简,即可判断正误.
【详解】
A:,,所以,,故,正确;
B:,,所以,同理,故不一定相等,错误;
C:由题意得:,,正确;
D:由题意得:,
,故一般来说故错误;
故选:AC
7.(2021·天津·高考真题)在边长为1的等边三角形ABC中,D为线段BC上的动点,且交AB于点E.且交AC于点F,则的值为____________;的最小值为____________.
【答案】 1
【解析】
设,,为边长为1的等边三角形,,
,
,为边长为的等边三角形,,
,
,
,
所以当时,的最小值为.
故答案为:1;.
8.(2020·天津·高考真题)如图,在四边形中,,,且,则实数的值为_________,若是线段上的动点,且,则的最小值为_________.
【答案】
【解析】
,,,
,
解得,
以点为坐标原点,所在直线为轴建立如下图所示的平面直角坐标系,
,
∵,∴的坐标为,
∵又∵,则,设,则(其中),
,,
,
所以,当时,取得最小值.
9.(2020·北京·高考真题)已知正方形的边长为2,点P满足,则_________;_________.
【答案】
【解析】
以点为坐标原点,.所在直线分别为.轴建立如下图所示的平面直角坐标系,
则点...,
,
则点,,,
因此,,.故答案为:;.
10.(2021·湖南·高考真题)已知向量,,则___________
【答案】
【解析】
,所以.故答案为:
11.(2021·全国·高考真题)已知向量,,,_______.
【答案】
【解析】
由已知可得,
因此,.故答案为:.
12.(2021·全国·高考真题(理))已知向量,若,则__________.
【答案】
【解析】因为,所以由可得,
,解得.故答案为:.
13.(2021·全国·高考真题(文))若向量满足,则_________.
【答案】
【解析】∵,∴
∴.故答案为:.
14.(2020·全国·高考真题(理))已知单位向量,的夹角为45°,与垂直,则k=__________.
【答案】
【解析】由题意可得:,
由向量垂直的充分必要条件可得:,
即:,解得:.
故答案为:.
复数部分
1.(2021·江苏·高考真题)若复数满足,则的虚部等于( )
A.4 B.2 C.-2 D.-4
【答案】C
【解析】若复数满足,则,
所以的虚部等于.故选:C.
2.(2021·全国·高考真题)复数在复平面内对应的点所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】A
【解析】,所以该复数对应的点为,
该点在第一象限,故选:A.
3.(2021·北京·高考真题)在复平面内,复数满足,则( )
A. B. C. D.
【答案】D
【解析】由题意可得:.故选:D.
4.(2021·全国·高考真题(文))已知,则( )
A. B. C. D.
【答案】B
【解析】,.故选:B.
5.(2021·全国·高考真题(理))设,则( )
A. B. C. D.
【答案】C
【解析】设,则,则,
所以,,解得,因此,.故选:C.
6.(2021·浙江·高考真题)已知,,(i为虚数单位),则( )
A. B.1 C. D.3
【答案】C
【解析】,
利用复数相等的充分必要条件可得:.故选:C.
7.(2020·北京·高考真题)在复平面内,复数对应的点的坐标是,则( ).
A. B. C. D.
【答案】B
【解析】由题意得,.故选:B.
8.(2020·浙江·高考真题)已知a∈R,若a–1+(a–2)i(i为虚数单位)是实数,则a=( )
A.1 B.–1 C.2 D.–2
【答案】C
【解析】因为为实数,所以,故选:C
9.(2020·全国·高考真题(文))(1–i)4=( )
A.–4 B.4
C.–4i D.4i
【答案】A
【解析】
.故选:A.
10.(2021·天津·高考真题)是虚数单位,复数_____________.
【答案】
【解析】.故答案为:.
11.(2020·天津·高考真题)是虚数单位,复数_________.
【答案】
【解析】
.
故答案为:.
12.(2020·江苏·高考真题)已知是虚数单位,则复数的实部是_____.
【答案】3
【解析】
∵复数
∴
∴复数的实部为3.
13.(2020·全国·高考真题(理))设复数,满足,,则=__________.
【答案】
【解析】方法一:设,,
,
,又,所以,,
.
故答案为:.
方法二:如图所示,设复数所对应的点为,,
由已知,
∴平行四边形为菱形,且都是正三角形,∴,
∴.
同课章节目录
