1.1 集合的概念 课件(共32张PPT)
文档属性
| 名称 | 1.1 集合的概念 课件(共32张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 850.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-23 22:38:36 | ||
图片预览






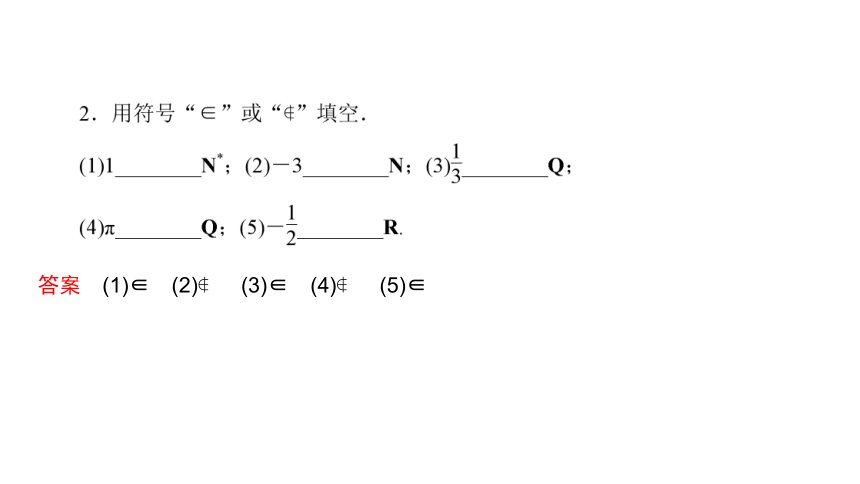




文档简介
(共32张PPT)
集合与常用逻辑用语
第一章
1.1 集合的概念
课程标准 学科素养
1.通过实例,了解集合的含义,理解元素与集合的属于关系.
2.针对具体问题,能在自然语言和图形语言的基础上,用符号语言刻画集合. 通过对集合概念的学习,提升“数学抽象”、“逻辑推理”的核心素养.
栏目索引
课前自主预习
课堂互动探究
随堂本课小结
课前自主预习
(1)元素:一般地,把______________统称为元素,常用小写的拉丁字母__________________表示.
(2)集合:把一些__________组成的总体叫做集合,简称________,常用大写拉丁字母__________________表示.
(3)集合相等:构成两个集合的元素是__________的.
(4)集合中元素的特性:____________、____________和无序性.
研究对象
知识点1 集合相关概念
a,b,c…
元素
集
A,B,C…
一样
确定性
互异性
[微思考]
(1)本班所有的“帅哥”能否构成一个集合?
(2)一个集合中可以有相同的元素吗?
提示:(1)某班所有的“帅哥”不能构成集合,因为“帅哥”没有明确的标准.
(2)根据集合元素的互异性可知,集合中不能有相同的元素.
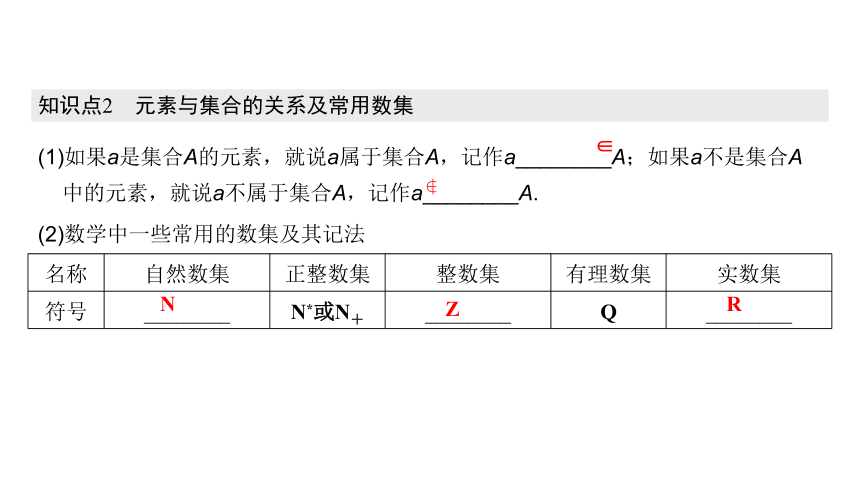
(1)如果a是集合A的元素,就说a属于集合A,记作a________A;如果a不是集合A中的元素,就说a不属于集合A,记作a________A.
(2)数学中一些常用的数集及其记法
知识点2 元素与集合的关系及常用数集
∈
名称 自然数集 正整数集 整数集 有理数集 实数集
符号 ________ N*或N+ ________ Q ________
N
Z
R
[微体验]
1.设集合A只含有一个元素a,则下列各式正确的是( )
A.0∈A B.a A
C.a∈A D.a=A
答案 C
答案 (1)∈ (2) (3)∈ (4) (5)∈
(1)把集合的所有元素______________出来,并用____________________括起来表示集合的方法叫做____________.
(2)一般地,设A是一个集合,我们把集合A中所有具有共同特征P(x)的元素x所组成的集合表示为{x∈A|P(x)},这种表示集合的方法称为____________.
知识点3 集合的表示方法
一一列举
花括号“{}”
列举法
描述法
[微体验]
1.思考辨析
(1)由1,1,2,3组成的集合可用列举法表示为{1,1,2,3}.( )
(2)集合{(1,2)}中的元素是1和2.( )
(3)集合A={x|x-1=0}与集合B={1}表示同一个集合.( )
答案 (1)× (2)× (3)√
2.方程x2=4的解集用列举法表示为( )
A.{(-2,2)} B.{-2,2}
C.{-2} D.{2}
答案 B
解析 由x2=4得x=±2,故用列举法可表示为{-2,2}.
3.集合A={x∈Z|-2<x<3}的元素个数为( )
A.1 B.2
C.3 D.4
答案 D
解析 因为A={x∈Z|-2<x<3},所以x的取值为-1,0,1,2,共4个.
考察下列每组对象,能构成集合的是( )
①中国各地最美的乡村;
②直角坐标系中横、纵坐标相等的点;
③不小于3的自然数;
④2020年第32届奥运会所设比赛项目.
A.③④ B.②③④
C.②③ D.②④
课堂互动探究
探究一 集合的基本概念
答案 B
解析 ①中“最美”标准不明确,不符合确定性,②③④中的元素标准明确,均可构成集合.
[方法总结]
判断一组对象能否组成集合的标准及其关注点
(1)标准:判断一组对象能否组成集合,关键看该组对象是否满足确定性.如果该组对象满足确定性,就可以组成集合;否则,不能组成集合.
(2)关注点:利用集合的含义判断一组对象能否组成一个集合,应注意集合中元素的特性,即确定性、互异性和无序性.
答案 B
解析 根据各数集的意义可知,①②正确,③④错误.
探究二 元素与集合之间的关系
(2)已知集合A含有三个元素2,4,6,且当a∈A,有6-a∈A,那么a为( )
A.2 B.2或4
C.4 D.0
答案 B
解析 集合A含有三个元素2,4,6,且当a∈A,有6-a∈A,a=2∈A,6-a=4∈A,所以a=2,或者a=4∈A,6-a=2∈A,所以a=4,综上所述,a=2或4.故选B.
[方法总结]
判断元素和集合关系的两种方法
(1)直接法:
①使用前提:集合中的元素是直接给出的.
②判断方法:首先明确集合是由哪些元素构成,然后再判断该元素在已知集合中是否出现即可.
(2)推理法:
①使用前提:对于某些不便直接表示的集合.
②判断方法:首先明确已知集合的元素具有什么特征,然后判断该元素是否满足集合中元素所具有的特征即可.
[跟踪训练2] (1)已知集合A中元素满足2x+a>0,a∈R,若1 A,2∈A,则
( )
A.a>-4 B.a≤-2
C.-4<a<-2 D.-4<a≤-2
答案 D
(2)设集合D是满足方程y=x2的有序数对(x,y)的集合,则-1____D,(-1,1)____D.
解析 因为集合D中的元素是有序数对(x,y),而-1是数,所以-1 D,(-1,1)∈D.
答案 ∈
用列举法表示下列给定的集合.
(1)不大于10的非负偶数组成的集合A;
(2)小于8的质数组成的集合B;
(3)方程2x2-x-3=0的实数根组成的集合C;
(4)一次函数y=x+3与y=-2x+6的图象的交点组成的集合D.
探究三 列举法表示集合
[方法总结]
列举法表示集合的步骤
(1)分清元素:列举法表示集合,要分清是数集还是点集.
(2)书写集合:列元素时要做到不重复、不遗漏.
提醒:二元方程组的解集,函数的图象上的点形成的集合都是点的集合,一定要写成实数对的形式,元素与元素之间用“,”隔开,如{(2,3),(5,-1)}.
[跟踪训练3] 用列举法表示下列集合.
(1)由book中的字母组成的集合;
(2)方程(x-2)2+|y+1|=0的解集.
用描述法表示下列集合.
(1)所有正偶数组成的集合;
(2)不等式3x-2>4的解集;
(3)在平面直角坐标系中,第一、三象限内点的集合.
解 (1)正偶数都能被2整除,所以正偶数可以表示为x=2n,(n∈N*)的形式.
于是这个集合可以表示为{x|x=2n,n∈N*}.
(2)由3x-2>4,得x>2,故不等式的解集为{x|x>2}.
(3)第一、三象限中的点(x,y)满足xy>0,于是这个集合可以表示为{(x,y)|xy>0}.
探究四 描述法表示集合
[变式探究] 若将本例(3)改为“坐标平面内坐标轴上的点组成的集合”,如何用描述法表示?
解 坐标平面内,x轴上的点纵坐标为0,横坐标为任意实数;y轴上的点横坐标为0,纵坐标为任意实数.故坐标轴上的点满足xy=0.用集合表示为{(x,y)|xy=0}.
[方法技巧]
描述法表示集合的步骤
(1)确定集合中元素的特征.
(2)给出其满足的性质.
(3)根据描述法的形式写出其满足的集合.
解 (1)列举法:{6,7,8}.
(2)描述法:{x|x≤2,且x≠0,x∈R}.
(3)列举法:{(0,0),(2,0)}.
(4)描述法:{(x,y)|y=x,x≠0}.
1.集合中元素的三个特性
(1)确定性:指的是作为一个集合中的元素,必须是确定的,即一个集合一旦确定,某一个元素属不属于这个集合就确定了.这个特性通常被用来判断涉及的总体是否构成集合.
(2)互异性:集合中的元素必须是互异的,就是说,对于一个给定的集合,它的任何两个元素都是不同的.
(3)无序性:集合与其中元素的排列顺序无关,如由元素a,b,c与由元素b,a,c组成的集合是相等的集合.这个性质通常用来判断两个集合的关系.
随堂本课小结
2.元素a与集合A之间只有两种关系:a∈A,a A.
3.在用列举法表示集合时应注意
(1)元素间用分隔号“,”;(2)元素不重复;(3)元素无顺序;(4)列举法可表示有限集,也可以表示无限集.若集合中的元素个数比较少,则用列举法比较简单;若集合中的元素较多或无限,但出现一定的规律性,在不发生误解的情况下,也可以用列举法表示.
4.在用描述法表示集合时应注意
(1)弄清元素所具有的形式(即代表元素是什么),是数、还是有序实数对(点)、还是集合或其他形式;
(2)当题目中用了其他字母来描述元素所具有的属性时,要去伪存真(元素具有怎样的属性),而不能被表面的字母形式所迷惑.
集合与常用逻辑用语
第一章
1.1 集合的概念
课程标准 学科素养
1.通过实例,了解集合的含义,理解元素与集合的属于关系.
2.针对具体问题,能在自然语言和图形语言的基础上,用符号语言刻画集合. 通过对集合概念的学习,提升“数学抽象”、“逻辑推理”的核心素养.
栏目索引
课前自主预习
课堂互动探究
随堂本课小结
课前自主预习
(1)元素:一般地,把______________统称为元素,常用小写的拉丁字母__________________表示.
(2)集合:把一些__________组成的总体叫做集合,简称________,常用大写拉丁字母__________________表示.
(3)集合相等:构成两个集合的元素是__________的.
(4)集合中元素的特性:____________、____________和无序性.
研究对象
知识点1 集合相关概念
a,b,c…
元素
集
A,B,C…
一样
确定性
互异性
[微思考]
(1)本班所有的“帅哥”能否构成一个集合?
(2)一个集合中可以有相同的元素吗?
提示:(1)某班所有的“帅哥”不能构成集合,因为“帅哥”没有明确的标准.
(2)根据集合元素的互异性可知,集合中不能有相同的元素.
(1)如果a是集合A的元素,就说a属于集合A,记作a________A;如果a不是集合A中的元素,就说a不属于集合A,记作a________A.
(2)数学中一些常用的数集及其记法
知识点2 元素与集合的关系及常用数集
∈
名称 自然数集 正整数集 整数集 有理数集 实数集
符号 ________ N*或N+ ________ Q ________
N
Z
R
[微体验]
1.设集合A只含有一个元素a,则下列各式正确的是( )
A.0∈A B.a A
C.a∈A D.a=A
答案 C
答案 (1)∈ (2) (3)∈ (4) (5)∈
(1)把集合的所有元素______________出来,并用____________________括起来表示集合的方法叫做____________.
(2)一般地,设A是一个集合,我们把集合A中所有具有共同特征P(x)的元素x所组成的集合表示为{x∈A|P(x)},这种表示集合的方法称为____________.
知识点3 集合的表示方法
一一列举
花括号“{}”
列举法
描述法
[微体验]
1.思考辨析
(1)由1,1,2,3组成的集合可用列举法表示为{1,1,2,3}.( )
(2)集合{(1,2)}中的元素是1和2.( )
(3)集合A={x|x-1=0}与集合B={1}表示同一个集合.( )
答案 (1)× (2)× (3)√
2.方程x2=4的解集用列举法表示为( )
A.{(-2,2)} B.{-2,2}
C.{-2} D.{2}
答案 B
解析 由x2=4得x=±2,故用列举法可表示为{-2,2}.
3.集合A={x∈Z|-2<x<3}的元素个数为( )
A.1 B.2
C.3 D.4
答案 D
解析 因为A={x∈Z|-2<x<3},所以x的取值为-1,0,1,2,共4个.
考察下列每组对象,能构成集合的是( )
①中国各地最美的乡村;
②直角坐标系中横、纵坐标相等的点;
③不小于3的自然数;
④2020年第32届奥运会所设比赛项目.
A.③④ B.②③④
C.②③ D.②④
课堂互动探究
探究一 集合的基本概念
答案 B
解析 ①中“最美”标准不明确,不符合确定性,②③④中的元素标准明确,均可构成集合.
[方法总结]
判断一组对象能否组成集合的标准及其关注点
(1)标准:判断一组对象能否组成集合,关键看该组对象是否满足确定性.如果该组对象满足确定性,就可以组成集合;否则,不能组成集合.
(2)关注点:利用集合的含义判断一组对象能否组成一个集合,应注意集合中元素的特性,即确定性、互异性和无序性.
答案 B
解析 根据各数集的意义可知,①②正确,③④错误.
探究二 元素与集合之间的关系
(2)已知集合A含有三个元素2,4,6,且当a∈A,有6-a∈A,那么a为( )
A.2 B.2或4
C.4 D.0
答案 B
解析 集合A含有三个元素2,4,6,且当a∈A,有6-a∈A,a=2∈A,6-a=4∈A,所以a=2,或者a=4∈A,6-a=2∈A,所以a=4,综上所述,a=2或4.故选B.
[方法总结]
判断元素和集合关系的两种方法
(1)直接法:
①使用前提:集合中的元素是直接给出的.
②判断方法:首先明确集合是由哪些元素构成,然后再判断该元素在已知集合中是否出现即可.
(2)推理法:
①使用前提:对于某些不便直接表示的集合.
②判断方法:首先明确已知集合的元素具有什么特征,然后判断该元素是否满足集合中元素所具有的特征即可.
[跟踪训练2] (1)已知集合A中元素满足2x+a>0,a∈R,若1 A,2∈A,则
( )
A.a>-4 B.a≤-2
C.-4<a<-2 D.-4<a≤-2
答案 D
(2)设集合D是满足方程y=x2的有序数对(x,y)的集合,则-1____D,(-1,1)____D.
解析 因为集合D中的元素是有序数对(x,y),而-1是数,所以-1 D,(-1,1)∈D.
答案 ∈
用列举法表示下列给定的集合.
(1)不大于10的非负偶数组成的集合A;
(2)小于8的质数组成的集合B;
(3)方程2x2-x-3=0的实数根组成的集合C;
(4)一次函数y=x+3与y=-2x+6的图象的交点组成的集合D.
探究三 列举法表示集合
[方法总结]
列举法表示集合的步骤
(1)分清元素:列举法表示集合,要分清是数集还是点集.
(2)书写集合:列元素时要做到不重复、不遗漏.
提醒:二元方程组的解集,函数的图象上的点形成的集合都是点的集合,一定要写成实数对的形式,元素与元素之间用“,”隔开,如{(2,3),(5,-1)}.
[跟踪训练3] 用列举法表示下列集合.
(1)由book中的字母组成的集合;
(2)方程(x-2)2+|y+1|=0的解集.
用描述法表示下列集合.
(1)所有正偶数组成的集合;
(2)不等式3x-2>4的解集;
(3)在平面直角坐标系中,第一、三象限内点的集合.
解 (1)正偶数都能被2整除,所以正偶数可以表示为x=2n,(n∈N*)的形式.
于是这个集合可以表示为{x|x=2n,n∈N*}.
(2)由3x-2>4,得x>2,故不等式的解集为{x|x>2}.
(3)第一、三象限中的点(x,y)满足xy>0,于是这个集合可以表示为{(x,y)|xy>0}.
探究四 描述法表示集合
[变式探究] 若将本例(3)改为“坐标平面内坐标轴上的点组成的集合”,如何用描述法表示?
解 坐标平面内,x轴上的点纵坐标为0,横坐标为任意实数;y轴上的点横坐标为0,纵坐标为任意实数.故坐标轴上的点满足xy=0.用集合表示为{(x,y)|xy=0}.
[方法技巧]
描述法表示集合的步骤
(1)确定集合中元素的特征.
(2)给出其满足的性质.
(3)根据描述法的形式写出其满足的集合.
解 (1)列举法:{6,7,8}.
(2)描述法:{x|x≤2,且x≠0,x∈R}.
(3)列举法:{(0,0),(2,0)}.
(4)描述法:{(x,y)|y=x,x≠0}.
1.集合中元素的三个特性
(1)确定性:指的是作为一个集合中的元素,必须是确定的,即一个集合一旦确定,某一个元素属不属于这个集合就确定了.这个特性通常被用来判断涉及的总体是否构成集合.
(2)互异性:集合中的元素必须是互异的,就是说,对于一个给定的集合,它的任何两个元素都是不同的.
(3)无序性:集合与其中元素的排列顺序无关,如由元素a,b,c与由元素b,a,c组成的集合是相等的集合.这个性质通常用来判断两个集合的关系.
随堂本课小结
2.元素a与集合A之间只有两种关系:a∈A,a A.
3.在用列举法表示集合时应注意
(1)元素间用分隔号“,”;(2)元素不重复;(3)元素无顺序;(4)列举法可表示有限集,也可以表示无限集.若集合中的元素个数比较少,则用列举法比较简单;若集合中的元素较多或无限,但出现一定的规律性,在不发生误解的情况下,也可以用列举法表示.
4.在用描述法表示集合时应注意
(1)弄清元素所具有的形式(即代表元素是什么),是数、还是有序实数对(点)、还是集合或其他形式;
(2)当题目中用了其他字母来描述元素所具有的属性时,要去伪存真(元素具有怎样的属性),而不能被表面的字母形式所迷惑.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
