必修第一册5.1任意角和弧度制 同步练习(Word版含解析)
文档属性
| 名称 | 必修第一册5.1任意角和弧度制 同步练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 897.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 06:04:28 | ||
图片预览


文档简介
必修第一册 5.1 任意角和弧度制 同步练习
一、单选题
1.如图所示的复古时钟显示的时刻为,将时针与分针视为两条线段,则该时刻的时针与分针所夹的钝角为( )
A. B. C. D.
2.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积(弦×矢+矢),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为,弧长等于米的弧田,按照上述经验公式计算所得弧田面积是( )平方米.
A. B. C. D.
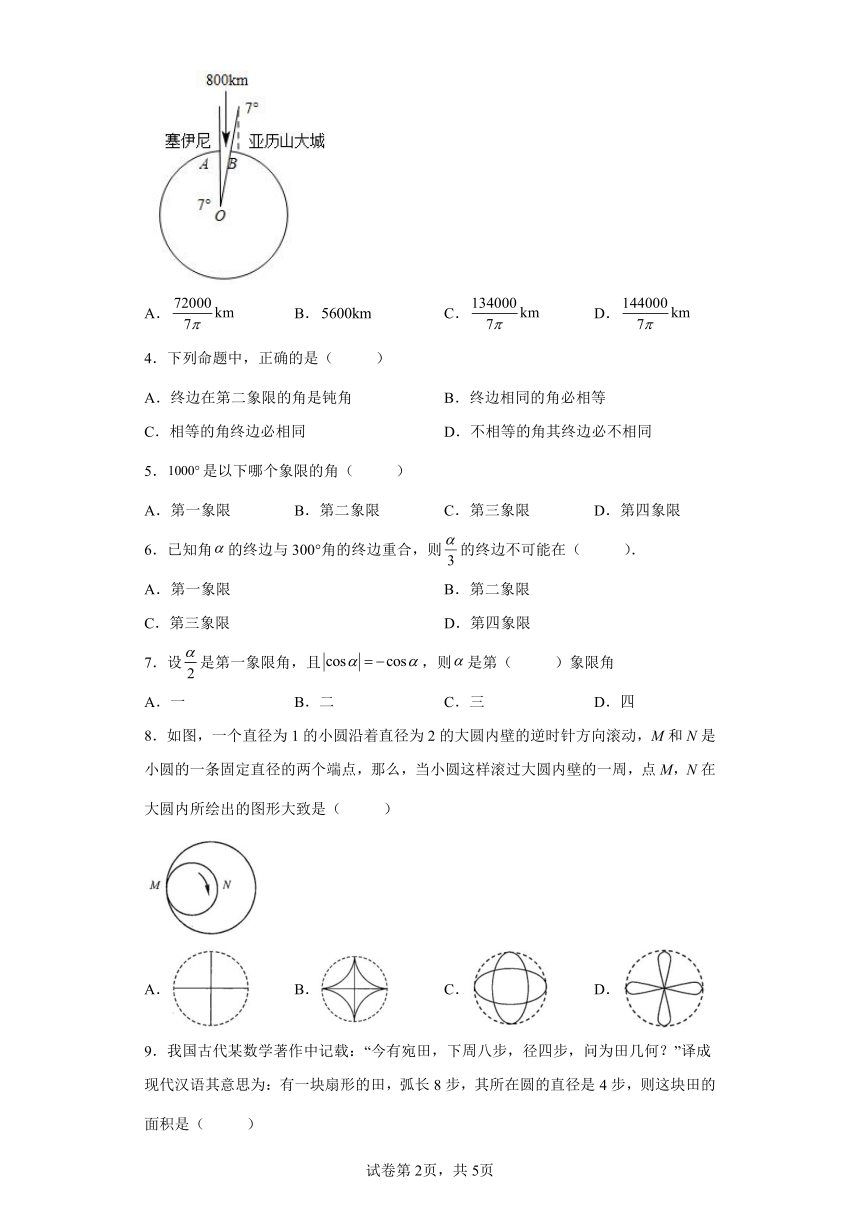
3.古希腊地理学家埃拉托色尼(Eratosthenes,前275一前193)用下面的方法估算地球的周长(即赤道周长).他从书中得知,位于尼罗河第一瀑布的塞伊尼(现在的阿斯旺,在北回归线上),夏至那天正午立杆无影;同样在夏至那天,他所在的城市——埃及北部的亚历山大城,立杆可测得日影角大约为(如图),埃拉托色尼猜想造成这个差异的原因是地球是圆的,并且因为太阳距离地球很远(现代科学观察得知,太阳光到达地球表面需要,光速),太阳光平行照射在地球上.根据平面几何知识,平行线内错角相等,因此日影角与两地对应的地心角相等,他又派人测得两地距离大约5000希腊里,约合:按照埃拉托色尼所得数据可以测算地球的半径约为( )
A. B. C. D.
4.下列命题中,正确的是( )
A.终边在第二象限的角是钝角 B.终边相同的角必相等
C.相等的角终边必相同 D.不相等的角其终边必不相同
5.是以下哪个象限的角( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知角的终边与300°角的终边重合,则的终边不可能在( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限
7.设是第一象限角,且,则是第( )象限角
A.一 B.二 C.三 D.四
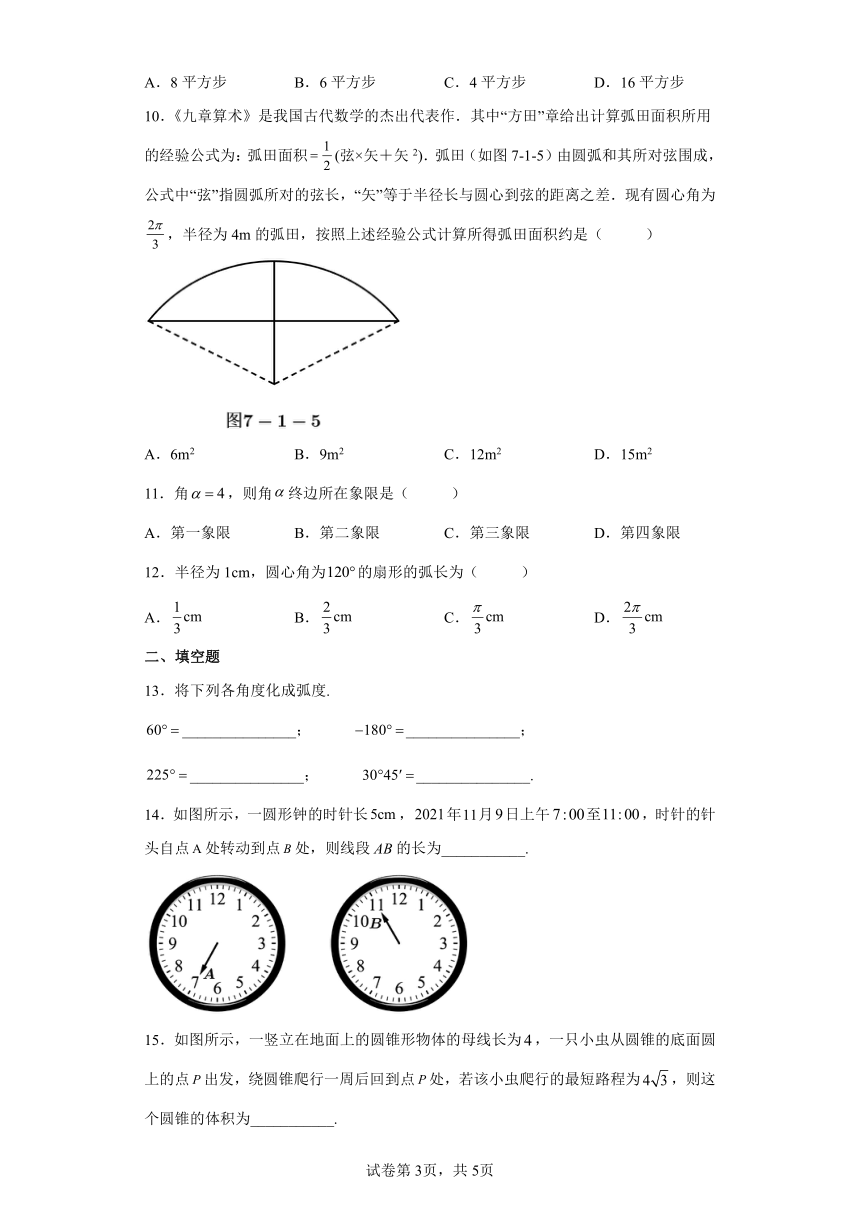
8.如图,一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方向滚动,M和N是小圆的一条固定直径的两个端点,那么,当小圆这样滚过大圆内壁的一周,点M,N在大圆内所绘出的图形大致是( )
A. B. C. D.
9.我国古代某数学著作中记载:“今有宛田,下周八步,径四步,问为田几何?”译成现代汉语其意思为:有一块扇形的田,弧长8步,其所在圆的直径是4步,则这块田的面积是( )
A.8平方步 B.6平方步 C.4平方步 D.16平方步
10.《九章算术》是我国古代数学的杰出代表作.其中“方田”章给出计算弧田面积所用的经验公式为:弧田面积(弦×矢+矢2).弧田(如图7-1-5)由圆弧和其所对弦围成,公式中“弦”指圆弧所对的弦长,“矢”等于半径长与圆心到弦的距离之差.现有圆心角为,半径为4m的弧田,按照上述经验公式计算所得弧田面积约是( )
A.6m2 B.9m2 C.12m2 D.15m2
11.角,则角终边所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.半径为1cm,圆心角为的扇形的弧长为( )
A. B. C. D.
二、填空题
13.将下列各角度化成弧度.
_______________; _______________;
_______________; _______________.
14.如图所示,一圆形钟的时针长,年月日上午至,时针的针头自点处转动到点处,则线段的长为___________.
15.如图所示,一竖立在地面上的圆锥形物体的母线长为,一只小虫从圆锥的底面圆上的点出发,绕圆锥爬行一周后回到点处,若该小虫爬行的最短路程为,则这个圆锥的体积为___________.
16.《九章算术》是我国古代内容极为丰富的数学名著,其中有这样一个问题:“今有宛田,下周三十步,径十六步.问为田几何?”其意思为:“有一块扇形的田,弧长为30步,其所在圆的直径为16步,问这块田的面积是多少平方步?”该问题的答案为___________平方步.
三、解答题
17.(1)写出与角终边相同的角的集合M;
(2)把角写成的形式,并指出其是第几象限角;
(3)若角且,求角.
18.已知角的终边在第四象限.
(1)试分别判断、是哪个象限的角;
(2)求的范围.
19.如图,已知圆O的半径r为10,弦AB的长为10.
(1)求弦AB所对的圆心角的大小;
(2)求圆心角所对应的弧长l及阴影部分的面积S.
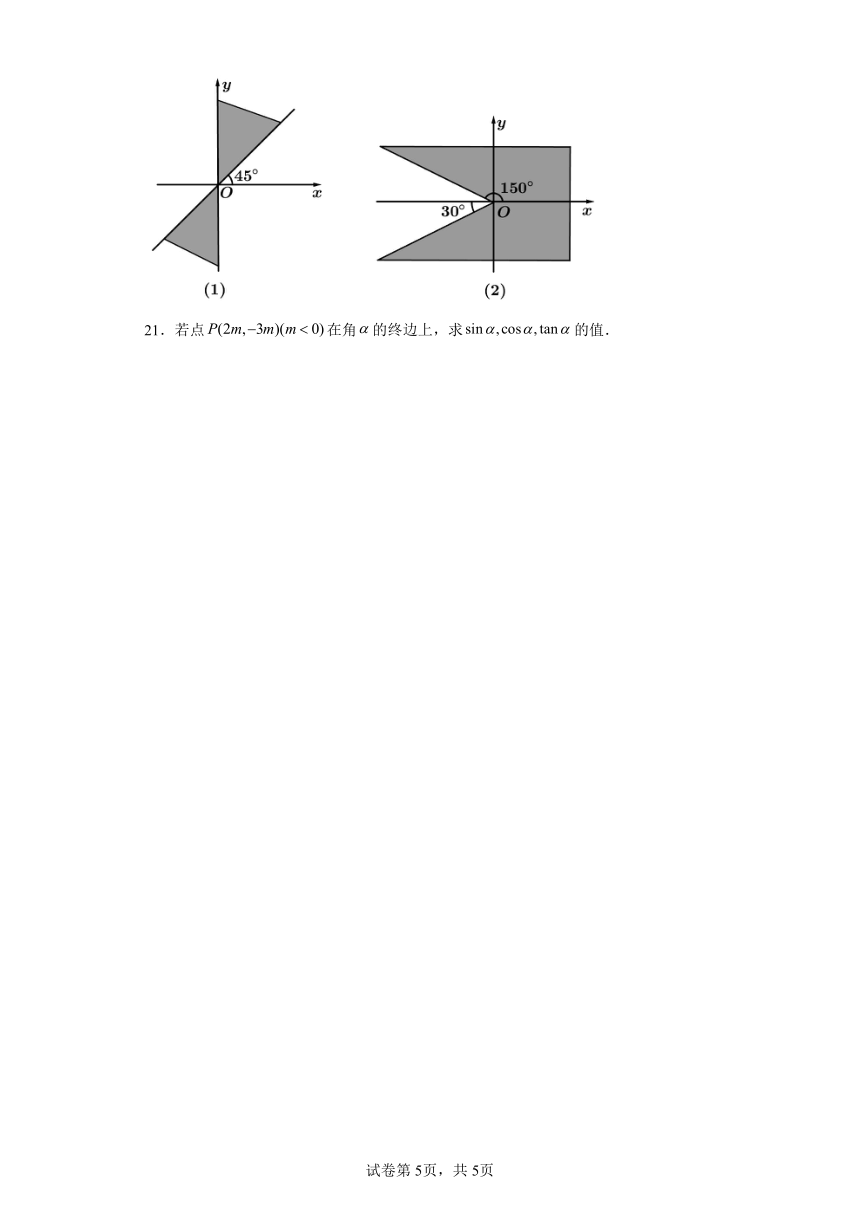
20.写出角的终边在图中阴影区域内的角的集合.(包括边界)
21.若点在角的终边上,求的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
首先确定当时针指向,分针指向时,时针与分针的夹角,减掉分针指向时,时针由向移动的弧度即可得到结果.
【详解】
表有个刻度,相邻两个刻度所对的圆心角为;
当时针指向,分针指向时,时针与分针夹角为;
但当分针指向时,时针由向移动了;
该时刻的时针与分针所夹钝角为.
故选:B.
2.D
由已知求得矢和弦长,再由公式计算.
【详解】
设半径为,则,,所以弦长为,
矢为,
所以弧田面积为.
故选:D.
3.D
根据,对应的弧长为,可求得地球的周长,代入公式,即可求得答案.
【详解】
由题意得:,对应的弧长为,
设地球的周长为C,地球半径为R,则,解得,
又,所以,解得,
所以按照埃拉托色尼所得数据可以测算地球的半径约为,
故选:D
4.C
根据终边相同的角的定义即可判断.
【详解】
-240°在第二象限但不是钝角,A错误;
60°和420°终边相同,但不相等,B错误;
由定义可知,C正确;
60°和420°不相等,但终边相同,D错误
故选:C.
5.D
首先写出终边相同的角的集合,再判断
【详解】
,角的终边在第四象限,所以角的终边也是第四象限.
故选:D
6.A
先求得的表达式,进而可得的表达式,对k赋值,分析即可得答案
【详解】
因为角的终边与300°角的终边重合,
所以,所以,
令,,终边位于第二象限;
令,,终边位于第三象限,
令,,终边位于第四象限,
令,,终边位于第二象限
所以的终边不可能在第一象限,
故选:A
7.B
计算得到,,再根据得到答案.
【详解】
∵是第一象限角,∴,,
∴,,
∴为第一象限角或第二象限角或终边在轴正半轴上的轴线角,
∵,∴,∴是第二象限角.
故选:.
本题考查了角度所在象限,意在考查学生的计算能力和转化能力.
8.A
设某时刻两圆相切于点,此时动点所处的位置为点,以切点在如图上运动为例,记直线与此时小圆的交点为,利用弧长公式计算,可知小圆的圆弧与圆弧的长相等,可得点与点重合,即动点在线段上运动,同理可知,此时点在与垂直的线段上运动,再通过观察四个选项可得答案.
【详解】
如图所示:
由题意可知,小圆总与大圆相内切,且小圆总经过大圆的圆心,
设某时刻两圆相切于点,此时动点所处的位置为点,
则大圆圆弧与小圆转过的圆弧相等,
以切点在如图上运动为例,记直线与此时小圆的交点为,
记,则,
所以,
所以大圆圆弧的长为,小圆圆弧的长为,
所以,
所以小圆的圆弧与圆弧的长相等,
所以点与点重合,即动点在线段上运动,
同理可知,此时点在与垂直的线段上运动,
点在其它位置类似可得,、的轨迹为互相垂直的线段.
观察四个选项可知,只有选项符合.
故选:A.
本题考查了弧长公式的应用,解题关键是利用弧长公式得到弧长相等.属于中档题.
9.A
根据扇形的面积公式即可求解.
【详解】
解:∵弧长8步,其所在圆的直径是4步,
∴(平方步),
故选:A.
10.B
根据题设条件计算出弦和矢,再代入弧田面积公式计算作答.
【详解】
依题意,弦(m),矢(m),
则弧田面积=(m2),
所以弧田面积约是9m2.
故选:B
11.C
根据,确定终边所在的象限.
【详解】
角
则角终边所在象限是第三象限.
故选:C
考查象限角的定义,属于基础题.
12.D
利用扇形弧长公式直接计算即可.
【详解】
圆心角化为弧度为,
则弧长为.
故选:D.
13.
根据角度制化弧度制的规则计算可得;
【详解】
解:,,,
故答案为:;;;
14.
计算出时针转过的弧度数,再结合锐角三角函数的定义可求得线段的长.
【详解】
年月日上午至,时针的针头自点处转动到点处,
则时针转过的弧度数为,故.
故答案为:.
15.
作出该圆锥的侧面展开图,该小虫爬行的最短路程为PP′,由余弦定理求出,求出底面圆的半径r,从而求出这个圆锥的高,由此能求出这个圆锥的体积.
【详解】
作出该圆锥的侧面展开图,如图所示:
该小虫爬行的最短路程为PP′,由余弦定理可得:
∴.
设底面圆的半径为r,则有,解得,
所以这个圆锥的高为,
则这个圆锥的体积为.
故答案为:.
立体几何中的翻折叠(展开)问题要注意翻折(展开)过程中的不变量.
16.120
利用扇形的面积公式求解.
【详解】
由题意得:扇形的弧长为30,半径为8,
所以扇形的面积为:,
故答案为:120
17.(1);(2),第四象限角;(3).
(1)根据,写出终边相等的角的集合即可.
(2)利用周期性,写出与终边相同的最小正角,进而判断所在的象限.
(3)由(1)所得范围,结合给定的范围写出角.
【详解】
(1)由终边相同的角的概念得:.
(2)∵,而是第四象限角,
∴是第四象限角.
(3),又且,
∴取得,.
18.(1)是第二或第四象限的角,是第三或第四象限或轴的非正半轴的角;(2)().
(1)先写出的范围,再求出和的范围,即可求解;
(2)由写出的范围,再求出的范围,再判断即可.
【详解】
是第四象限的角,
,
,
当时,
此时是第二象限;
当时,
此时是第四象限;
又
此时是第三象限或第四象限或轴的非正半轴;
(2)
19.(1)
(2);
(1)根据为等边三角形,可得,即可求解.
(2)利用扇形的弧长公式以及扇形的面积公式即可求解.
(1)
由于圆O的半径r为10,弦AB的长为10,
所以为等边三角形,,所以.
(2)
因为,所以,
.
又,
所以.
20.(1) (2)
由题意直接利用终边相同的角的集合的表示方法表示即可.
【详解】
解:(1)图中阴影区域内的角的集合为
(2)图中阴影区域内的角的集合为
21.,,.
先求出原点到点的距离,根据任意角的三角函数的定义求,,的值,然后代入式子运算.
【详解】
由题意,知点在第二象限,
且.
故,
,
.
本题考查任意角的三角函数的定义,,属于基础题.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图所示的复古时钟显示的时刻为,将时针与分针视为两条线段,则该时刻的时针与分针所夹的钝角为( )
A. B. C. D.
2.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积(弦×矢+矢),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为,弧长等于米的弧田,按照上述经验公式计算所得弧田面积是( )平方米.
A. B. C. D.
3.古希腊地理学家埃拉托色尼(Eratosthenes,前275一前193)用下面的方法估算地球的周长(即赤道周长).他从书中得知,位于尼罗河第一瀑布的塞伊尼(现在的阿斯旺,在北回归线上),夏至那天正午立杆无影;同样在夏至那天,他所在的城市——埃及北部的亚历山大城,立杆可测得日影角大约为(如图),埃拉托色尼猜想造成这个差异的原因是地球是圆的,并且因为太阳距离地球很远(现代科学观察得知,太阳光到达地球表面需要,光速),太阳光平行照射在地球上.根据平面几何知识,平行线内错角相等,因此日影角与两地对应的地心角相等,他又派人测得两地距离大约5000希腊里,约合:按照埃拉托色尼所得数据可以测算地球的半径约为( )
A. B. C. D.
4.下列命题中,正确的是( )
A.终边在第二象限的角是钝角 B.终边相同的角必相等
C.相等的角终边必相同 D.不相等的角其终边必不相同
5.是以下哪个象限的角( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知角的终边与300°角的终边重合,则的终边不可能在( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限
7.设是第一象限角,且,则是第( )象限角
A.一 B.二 C.三 D.四
8.如图,一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方向滚动,M和N是小圆的一条固定直径的两个端点,那么,当小圆这样滚过大圆内壁的一周,点M,N在大圆内所绘出的图形大致是( )
A. B. C. D.
9.我国古代某数学著作中记载:“今有宛田,下周八步,径四步,问为田几何?”译成现代汉语其意思为:有一块扇形的田,弧长8步,其所在圆的直径是4步,则这块田的面积是( )
A.8平方步 B.6平方步 C.4平方步 D.16平方步
10.《九章算术》是我国古代数学的杰出代表作.其中“方田”章给出计算弧田面积所用的经验公式为:弧田面积(弦×矢+矢2).弧田(如图7-1-5)由圆弧和其所对弦围成,公式中“弦”指圆弧所对的弦长,“矢”等于半径长与圆心到弦的距离之差.现有圆心角为,半径为4m的弧田,按照上述经验公式计算所得弧田面积约是( )
A.6m2 B.9m2 C.12m2 D.15m2
11.角,则角终边所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.半径为1cm,圆心角为的扇形的弧长为( )
A. B. C. D.
二、填空题
13.将下列各角度化成弧度.
_______________; _______________;
_______________; _______________.
14.如图所示,一圆形钟的时针长,年月日上午至,时针的针头自点处转动到点处,则线段的长为___________.
15.如图所示,一竖立在地面上的圆锥形物体的母线长为,一只小虫从圆锥的底面圆上的点出发,绕圆锥爬行一周后回到点处,若该小虫爬行的最短路程为,则这个圆锥的体积为___________.
16.《九章算术》是我国古代内容极为丰富的数学名著,其中有这样一个问题:“今有宛田,下周三十步,径十六步.问为田几何?”其意思为:“有一块扇形的田,弧长为30步,其所在圆的直径为16步,问这块田的面积是多少平方步?”该问题的答案为___________平方步.
三、解答题
17.(1)写出与角终边相同的角的集合M;
(2)把角写成的形式,并指出其是第几象限角;
(3)若角且,求角.
18.已知角的终边在第四象限.
(1)试分别判断、是哪个象限的角;
(2)求的范围.
19.如图,已知圆O的半径r为10,弦AB的长为10.
(1)求弦AB所对的圆心角的大小;
(2)求圆心角所对应的弧长l及阴影部分的面积S.
20.写出角的终边在图中阴影区域内的角的集合.(包括边界)
21.若点在角的终边上,求的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
首先确定当时针指向,分针指向时,时针与分针的夹角,减掉分针指向时,时针由向移动的弧度即可得到结果.
【详解】
表有个刻度,相邻两个刻度所对的圆心角为;
当时针指向,分针指向时,时针与分针夹角为;
但当分针指向时,时针由向移动了;
该时刻的时针与分针所夹钝角为.
故选:B.
2.D
由已知求得矢和弦长,再由公式计算.
【详解】
设半径为,则,,所以弦长为,
矢为,
所以弧田面积为.
故选:D.
3.D
根据,对应的弧长为,可求得地球的周长,代入公式,即可求得答案.
【详解】
由题意得:,对应的弧长为,
设地球的周长为C,地球半径为R,则,解得,
又,所以,解得,
所以按照埃拉托色尼所得数据可以测算地球的半径约为,
故选:D
4.C
根据终边相同的角的定义即可判断.
【详解】
-240°在第二象限但不是钝角,A错误;
60°和420°终边相同,但不相等,B错误;
由定义可知,C正确;
60°和420°不相等,但终边相同,D错误
故选:C.
5.D
首先写出终边相同的角的集合,再判断
【详解】
,角的终边在第四象限,所以角的终边也是第四象限.
故选:D
6.A
先求得的表达式,进而可得的表达式,对k赋值,分析即可得答案
【详解】
因为角的终边与300°角的终边重合,
所以,所以,
令,,终边位于第二象限;
令,,终边位于第三象限,
令,,终边位于第四象限,
令,,终边位于第二象限
所以的终边不可能在第一象限,
故选:A
7.B
计算得到,,再根据得到答案.
【详解】
∵是第一象限角,∴,,
∴,,
∴为第一象限角或第二象限角或终边在轴正半轴上的轴线角,
∵,∴,∴是第二象限角.
故选:.
本题考查了角度所在象限,意在考查学生的计算能力和转化能力.
8.A
设某时刻两圆相切于点,此时动点所处的位置为点,以切点在如图上运动为例,记直线与此时小圆的交点为,利用弧长公式计算,可知小圆的圆弧与圆弧的长相等,可得点与点重合,即动点在线段上运动,同理可知,此时点在与垂直的线段上运动,再通过观察四个选项可得答案.
【详解】
如图所示:
由题意可知,小圆总与大圆相内切,且小圆总经过大圆的圆心,
设某时刻两圆相切于点,此时动点所处的位置为点,
则大圆圆弧与小圆转过的圆弧相等,
以切点在如图上运动为例,记直线与此时小圆的交点为,
记,则,
所以,
所以大圆圆弧的长为,小圆圆弧的长为,
所以,
所以小圆的圆弧与圆弧的长相等,
所以点与点重合,即动点在线段上运动,
同理可知,此时点在与垂直的线段上运动,
点在其它位置类似可得,、的轨迹为互相垂直的线段.
观察四个选项可知,只有选项符合.
故选:A.
本题考查了弧长公式的应用,解题关键是利用弧长公式得到弧长相等.属于中档题.
9.A
根据扇形的面积公式即可求解.
【详解】
解:∵弧长8步,其所在圆的直径是4步,
∴(平方步),
故选:A.
10.B
根据题设条件计算出弦和矢,再代入弧田面积公式计算作答.
【详解】
依题意,弦(m),矢(m),
则弧田面积=(m2),
所以弧田面积约是9m2.
故选:B
11.C
根据,确定终边所在的象限.
【详解】
角
则角终边所在象限是第三象限.
故选:C
考查象限角的定义,属于基础题.
12.D
利用扇形弧长公式直接计算即可.
【详解】
圆心角化为弧度为,
则弧长为.
故选:D.
13.
根据角度制化弧度制的规则计算可得;
【详解】
解:,,,
故答案为:;;;
14.
计算出时针转过的弧度数,再结合锐角三角函数的定义可求得线段的长.
【详解】
年月日上午至,时针的针头自点处转动到点处,
则时针转过的弧度数为,故.
故答案为:.
15.
作出该圆锥的侧面展开图,该小虫爬行的最短路程为PP′,由余弦定理求出,求出底面圆的半径r,从而求出这个圆锥的高,由此能求出这个圆锥的体积.
【详解】
作出该圆锥的侧面展开图,如图所示:
该小虫爬行的最短路程为PP′,由余弦定理可得:
∴.
设底面圆的半径为r,则有,解得,
所以这个圆锥的高为,
则这个圆锥的体积为.
故答案为:.
立体几何中的翻折叠(展开)问题要注意翻折(展开)过程中的不变量.
16.120
利用扇形的面积公式求解.
【详解】
由题意得:扇形的弧长为30,半径为8,
所以扇形的面积为:,
故答案为:120
17.(1);(2),第四象限角;(3).
(1)根据,写出终边相等的角的集合即可.
(2)利用周期性,写出与终边相同的最小正角,进而判断所在的象限.
(3)由(1)所得范围,结合给定的范围写出角.
【详解】
(1)由终边相同的角的概念得:.
(2)∵,而是第四象限角,
∴是第四象限角.
(3),又且,
∴取得,.
18.(1)是第二或第四象限的角,是第三或第四象限或轴的非正半轴的角;(2)().
(1)先写出的范围,再求出和的范围,即可求解;
(2)由写出的范围,再求出的范围,再判断即可.
【详解】
是第四象限的角,
,
,
当时,
此时是第二象限;
当时,
此时是第四象限;
又
此时是第三象限或第四象限或轴的非正半轴;
(2)
19.(1)
(2);
(1)根据为等边三角形,可得,即可求解.
(2)利用扇形的弧长公式以及扇形的面积公式即可求解.
(1)
由于圆O的半径r为10,弦AB的长为10,
所以为等边三角形,,所以.
(2)
因为,所以,
.
又,
所以.
20.(1) (2)
由题意直接利用终边相同的角的集合的表示方法表示即可.
【详解】
解:(1)图中阴影区域内的角的集合为
(2)图中阴影区域内的角的集合为
21.,,.
先求出原点到点的距离,根据任意角的三角函数的定义求,,的值,然后代入式子运算.
【详解】
由题意,知点在第二象限,
且.
故,
,
.
本题考查任意角的三角函数的定义,,属于基础题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
