华师大版八下数学 17.4.1反比例函数 复习 教案
文档属性
| 名称 | 华师大版八下数学 17.4.1反比例函数 复习 教案 |

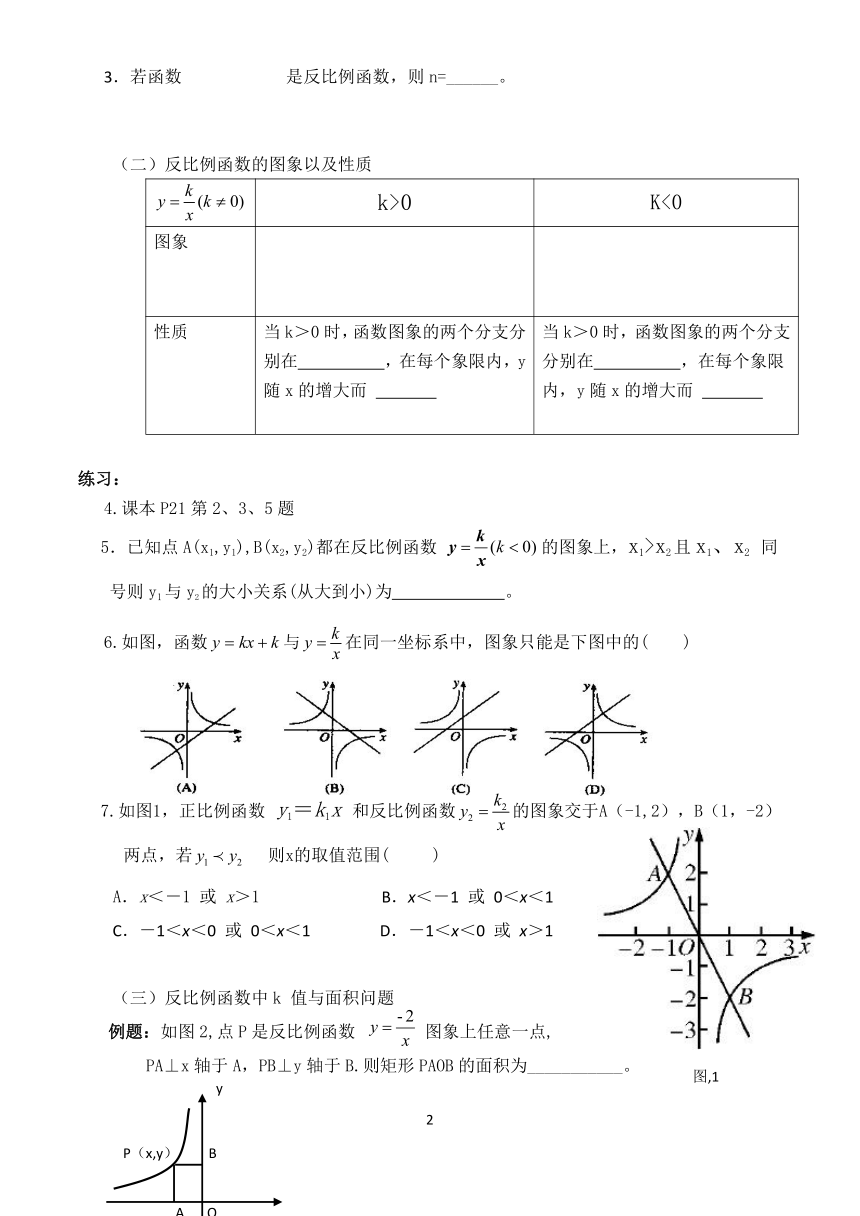
|
|
| 格式 | doc | ||
| 文件大小 | 316.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 17:58:27 | ||
图片预览

文档简介
反比例函数单元复习
教学目的:
知识与技能
1. 让学生回顾整章的内容,系统把握整章的的知识要点和基本技能,
2. 能运用反比例函数图像以及一次函数的图像,解决一次函数和反比例函数结合的问题。
过程与方法
通过对知识的归纳,以及练习题中对图像的分析,向学生渗透数形结合的思想方法,并通过 图像的直观加强学生认识反比例图像的特征.
情感态度和价值观
1.让学生体会事物是由规律地变化着的观点
2.通过问题的分析和探究,培养学生分析问题,解决问题的能力,使学生感受到生活中处处有数学,增加学生对数学的兴趣。
学情分析:通过前期作业的批改以及跟学生的交谈,了解到部分学生对于反比例函数的图像以及性质掌握不清,以致无法运用反比例函数图象来解决实际问题。但大部分学生对于反比例图象都有较浓厚的兴趣,喜欢探究。
教学重点:反比例函数的定义以及性质的掌握和运用。
教学难点:反比例函数与一次函数的综合运用。
教学过程:
1、 由反比例函数的知识网络引入
二、知识点回顾与应用练习
(一)反比例函数的定义和解析式
一般地,形如 ______________( )的函数称为反比例函数。(其中,自变量x的取值范围为____________)。
练习:
1.下列哪些是反比例函数
1 ② ③
④ ⑤ ⑥ 中,y是x的反比例函数的有 (填序号)
2.已知点A(3,-4)是反比例函数上的点,则反比例函数的解析式为
3.若函数 是反比例函数,则n=______。
(二)反比例函数的图象以及性质
k>0 K<0
图象
性质 当k>0时,函数图象的两个分支分别在 ,在每个象限内,y随x的增大而 当k>0时,函数图象的两个分支分别在 ,在每个象限内,y随x的增大而
练习:
4.课本P21第2、3、5题
5.已知点A(x1,y1),B(x2,y2)都在反比例函数 的图象上,x1>x2且x1、x2 同号则y1与y2的大小关系(从大到小)为 。
6.如图,函数与在同一坐标系中,图象只能是下图中的( )
7.如图1,正比例函数 y1=k1x 和反比例函数的图象交于A(-1,2),B(1,-2)两点,若 则x的取值范围( )
A.x<-1 或 x>1 B.x<-1 或 0<x<1
C.-1<x<0 或 0<x<1 D.-1<x<0 或 x>1
(三)反比例函数中k 值与面积问题
例题:如图2,点P是反比例函数 图象上任意一点,
PA⊥x轴于A,PB⊥y轴于B.则矩形PAOB的面积为___________。
练习:
8.如图3,点A在双曲线上,AB⊥x轴于B,且△ABC的面积为2,则K= 。
9.如图4,点A、B在双曲线上的点,分别过A、B两点作X轴,y轴作垂线段,若,则 。
(四)反比例函数的实际应用
病人按规定的剂量服用某种药物,测得服药后 2小时,每毫升血液中的含药量达到最大值为 4 毫克。已知服药后,2 小时前每毫升血液中的含药量 y(单位:毫克)与时间 x(单位:小时)成正比例;2 小时后 y 与 x 成反比例(如图5)。根据以上信息解答下列问题
(1)求当 0 ≤ x ≤ 2 时,y 与 x 的函数关系式;
(2)求当 x > 2 时,y 与 x 的函数关系式
(3)若每毫升血液中的含药量不低于 2 毫克时治疗有效,则服药一次,治疗疾病有效时间是多长?
三、反比例函数与一次函数综合应用
如图5,已知反比例函数的图象经过点,直线经过该反比例函数图象上的点Q(4,m)。
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与 x 轴、y 轴分别相交于 A、B 两点,与反比例函数图象的另一个交点为 P,连接 OP,OQ,求△OPQ 的面积?
4、 课堂小结
1、反比例函数的一般形式
2、求反比例函数解析式的方法
3、反比例函数的图象与性质
五、课后作业
1.如图6:一次函数 的图象与反比例函数 的图象交于M(2,m)、
N(-1,-4)两点。
(1)求反比例函数和一次函数的解析式;
(2)当x为何值时,反比例函数的函数值大于一次函数的函数值?
图,1
y
A O
P(x,y) B
x
y
-1 0 2
N(-1,-4)
M(2,m)
图2
图3
图4
反比例函数
定义和解析式
图象与性质
实际应用
图5
图5
图6
4
教学目的:
知识与技能
1. 让学生回顾整章的内容,系统把握整章的的知识要点和基本技能,
2. 能运用反比例函数图像以及一次函数的图像,解决一次函数和反比例函数结合的问题。
过程与方法
通过对知识的归纳,以及练习题中对图像的分析,向学生渗透数形结合的思想方法,并通过 图像的直观加强学生认识反比例图像的特征.
情感态度和价值观
1.让学生体会事物是由规律地变化着的观点
2.通过问题的分析和探究,培养学生分析问题,解决问题的能力,使学生感受到生活中处处有数学,增加学生对数学的兴趣。
学情分析:通过前期作业的批改以及跟学生的交谈,了解到部分学生对于反比例函数的图像以及性质掌握不清,以致无法运用反比例函数图象来解决实际问题。但大部分学生对于反比例图象都有较浓厚的兴趣,喜欢探究。
教学重点:反比例函数的定义以及性质的掌握和运用。
教学难点:反比例函数与一次函数的综合运用。
教学过程:
1、 由反比例函数的知识网络引入
二、知识点回顾与应用练习
(一)反比例函数的定义和解析式
一般地,形如 ______________( )的函数称为反比例函数。(其中,自变量x的取值范围为____________)。
练习:
1.下列哪些是反比例函数
1 ② ③
④ ⑤ ⑥ 中,y是x的反比例函数的有 (填序号)
2.已知点A(3,-4)是反比例函数上的点,则反比例函数的解析式为
3.若函数 是反比例函数,则n=______。
(二)反比例函数的图象以及性质
k>0 K<0
图象
性质 当k>0时,函数图象的两个分支分别在 ,在每个象限内,y随x的增大而 当k>0时,函数图象的两个分支分别在 ,在每个象限内,y随x的增大而
练习:
4.课本P21第2、3、5题
5.已知点A(x1,y1),B(x2,y2)都在反比例函数 的图象上,x1>x2且x1、x2 同号则y1与y2的大小关系(从大到小)为 。
6.如图,函数与在同一坐标系中,图象只能是下图中的( )
7.如图1,正比例函数 y1=k1x 和反比例函数的图象交于A(-1,2),B(1,-2)两点,若 则x的取值范围( )
A.x<-1 或 x>1 B.x<-1 或 0<x<1
C.-1<x<0 或 0<x<1 D.-1<x<0 或 x>1
(三)反比例函数中k 值与面积问题
例题:如图2,点P是反比例函数 图象上任意一点,
PA⊥x轴于A,PB⊥y轴于B.则矩形PAOB的面积为___________。
练习:
8.如图3,点A在双曲线上,AB⊥x轴于B,且△ABC的面积为2,则K= 。
9.如图4,点A、B在双曲线上的点,分别过A、B两点作X轴,y轴作垂线段,若,则 。
(四)反比例函数的实际应用
病人按规定的剂量服用某种药物,测得服药后 2小时,每毫升血液中的含药量达到最大值为 4 毫克。已知服药后,2 小时前每毫升血液中的含药量 y(单位:毫克)与时间 x(单位:小时)成正比例;2 小时后 y 与 x 成反比例(如图5)。根据以上信息解答下列问题
(1)求当 0 ≤ x ≤ 2 时,y 与 x 的函数关系式;
(2)求当 x > 2 时,y 与 x 的函数关系式
(3)若每毫升血液中的含药量不低于 2 毫克时治疗有效,则服药一次,治疗疾病有效时间是多长?
三、反比例函数与一次函数综合应用
如图5,已知反比例函数的图象经过点,直线经过该反比例函数图象上的点Q(4,m)。
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与 x 轴、y 轴分别相交于 A、B 两点,与反比例函数图象的另一个交点为 P,连接 OP,OQ,求△OPQ 的面积?
4、 课堂小结
1、反比例函数的一般形式
2、求反比例函数解析式的方法
3、反比例函数的图象与性质
五、课后作业
1.如图6:一次函数 的图象与反比例函数 的图象交于M(2,m)、
N(-1,-4)两点。
(1)求反比例函数和一次函数的解析式;
(2)当x为何值时,反比例函数的函数值大于一次函数的函数值?
图,1
y
A O
P(x,y) B
x
y
-1 0 2
N(-1,-4)
M(2,m)
图2
图3
图4
反比例函数
定义和解析式
图象与性质
实际应用
图5
图5
图6
4
