第九章 统计 基础卷(Word版含解析)
文档属性
| 名称 | 第九章 统计 基础卷(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 384.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 00:00:00 | ||
图片预览




文档简介
必修二第九章统计(基础卷)
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 12 小题 ,每题 5 分 ,共计60分 , )
1. 为了了解全校名高一学生的身高情况,从中抽取名学生进行测量.下列说法正确的是( )
A.总体是名 B.个体是每一个学生
C.样本是名学生 D.样本容量是
2. 在“世界读书日”前夕,为了了解某地名居民某天的阅读时间,从中抽取了名居民的阅读时间进行统计分析,在这个问题中,名居民的阅读时间的全体是( )
A.总体 B.个体
C.样本的容量 D.从总体中抽取的一个样本
3. 已知一个样本中的数据为,,,,,则这样的样本标准差为
A. B. C. D.
4. 某中学初中部共有名教师,高中部共有名教师,其性别比例如图所示,则该校女教师的人数为( )
A. B. C. D.
5. 总体由编号为,,…,,的个个体组成.利用下面的随机数表选取个个体,选取方法从随机数表第行的第列和第列数字开始由左到右依次选取两个数字,则选出来的第个个体的编号为( )
A. B. C. D.
6. 某公司在甲、乙、丙、丁四个地区分别有 个、个、 个、 个销售点,公司为了调查产品的销售情况,需从这个销售点中抽取一个容量为的样本,记这项调查为①;在丙地区有个特大型销售点,要从中抽取个销售点调查其销售收入和售后服务等情况,记这项调查为②,则完成①②这两项调查宜采用的抽样方法依次为
A.分层抽样法,系统抽样法
B.分层抽样法,简单随机抽样法
C.系统抽样法,分层抽样法
D.简单随机抽样法,分层抽样法
7. 从某批零件中抽取个,然后再从个中抽出个进行合格检查,发现合格品有个,则该批产品的合格率为( )
A. B. C. D.
8. 一个社会调查机构就某地居民的月收入调查了人,并根据所得数据画了样本的频率分布直方图(如图),为了分析居民的收入与年龄、学历、职业等方面的关系,要从这人中再用分层抽样方法抽出人作进一步调查,则在(元)月收入段应抽出的人数为( )
A. B. C. D.
9. 总体由编号为,,,,的个个体组成,利用下面的随机数表选取个个体,选取方法是从随机数表第行的第列和第列数字开始由左到右依次选取两个数字,则选出来的第个个体的编号为( )
A. B. C. D.
10. 一个总体的个个体的编号分别为,,,,,现需从中抽取一个容量为的样本,请从随机数表的倒数第行(表中为随机数表的最后行)第列开始向右读取,直到取足样本,则抽取的最后一个个体的号码是( )
A. B. C. D.
11. 某学校在校学生人,为了迎接年亚运会,学校举行了亚运会跑步和爬山比赛活动,每人都参加而且只参加其中一项比赛,各年级参与比赛人数情况如下表:
高一级 高二级 高三级
跑步
爬山
其中,全校参与爬山的人数占总人数的.为了了解学生对本次活动的满意程度,从中抽取一个人的样本进行调查,则高三参与跑步的学生中应抽取( )
A.人 B.人 C.人 D.人
12. 从个篮球中任取一个,检查其质量,用随机数法抽取样本,则应编号为
A.,,,,,,,,,
B.,,,,,,,,,
C.,,,,,,,,,
D.,,,,,,,,,
二、 填空题 (本题共计 4 小题 ,每题 5 分 ,共计20分 , )
13. 年初,我国黑龙江省县发现多起新冠肺炎病例.某医院决定派出一支医疗队前往县支援抗疫工作,该医院职工踊跃报名,其中报名的医生人,护士人,医技人,该医院决定采用分层抽样的方法,从中抽取人组成抗疫医疗队,若医生和护士共抽取了人,则________.
14. 某高校招生计划一直在按﹕﹕录取一本、二本、三本新生.若年计划录取的三本人数为人,那么,年录取的二本人数比一本人数多录取的人数为________.
15. 某市有大型超市家、中型超市家、小型超市家.为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为的样本,应抽取中型超市________家.
16. 我国西部一个地区的年降水量在下列区间内的概率如表所示
年降水量
概 率
则年降水量在范围内的概率是________.
三、 解答题 (本题共计 6 小题 ,共计70分 , )
17.(10分) 名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
(1)求频率分布直方图中的值;
(2)估计总体中成绩落在中的学生人数;
(3)根据频率分布直方图估计名学生数学考试成绩的众数,中位数.
18.(12分) 指出下列抽样采用的是哪一种抽样方法?
(1)为险测产品质量,从流水线上每隔一小时抽取一件产品进行检验;
(2)某班分到张电影票,通过抽签的方法确定看电影的同学;
(3)某小学为了解学生的近视情况,从到年级中按年级学生比例共抽取名学生测量他们的视力;
(4)某校在初一招生中,因报名人数超过录取人数,采用摇号的方法产生录取名单.
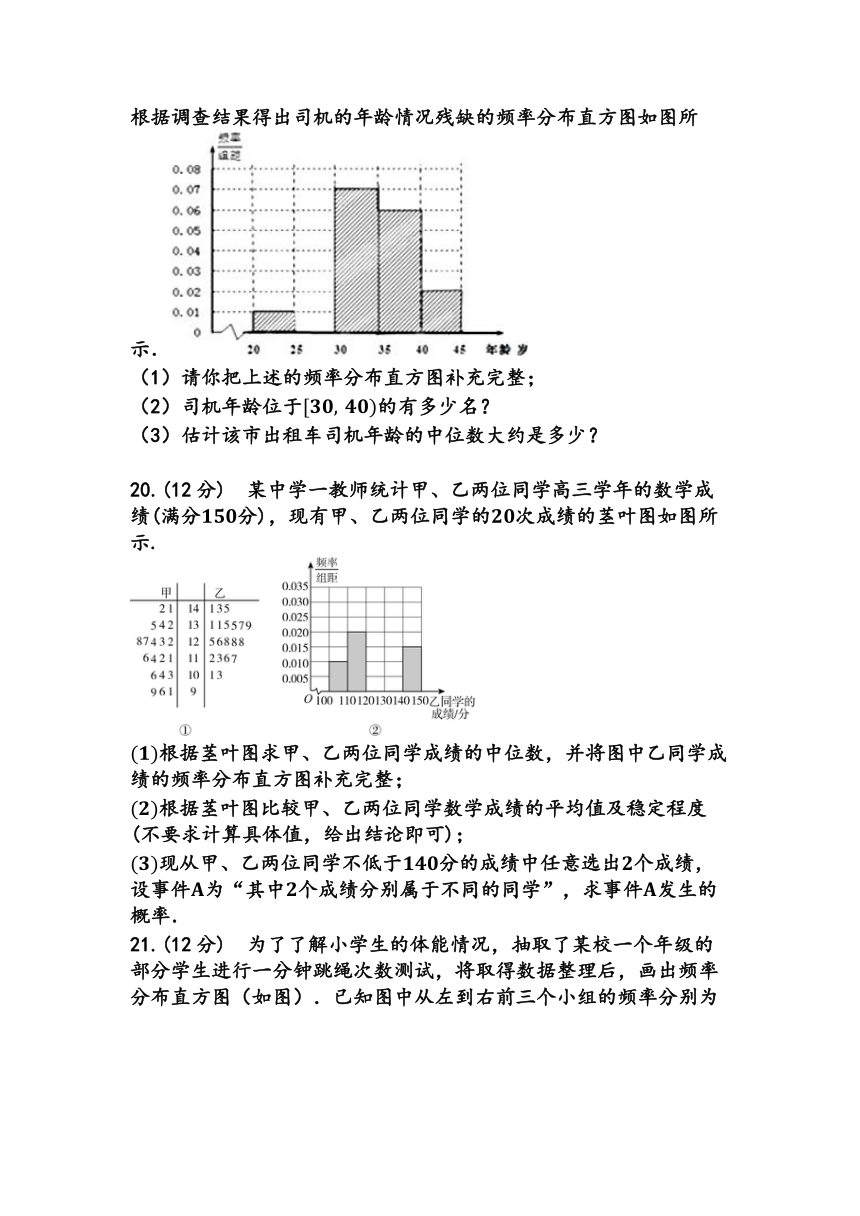
19.(12分) 某市要对多名出租车司机的年龄进行调查,现从中随机抽出名司机,已知抽到的司机年龄都在岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示.
(1)请你把上述的频率分布直方图补充完整;
(2)司机年龄位于的有多少名?
(3)估计该市出租车司机年龄的中位数大约是多少?
20.(12分) 某中学一教师统计甲、乙两位同学高三学年的数学成绩(满分分),现有甲、乙两位同学的次成绩的茎叶图如图所示.
根据茎叶图求甲、乙两位同学成绩的中位数,并将图中乙同学成绩的频率分布直方图补充完整;
根据茎叶图比较甲、乙两位同学数学成绩的平均值及稳定程度(不要求计算具体值,给出结论即可);
现从甲、乙两位同学不低于分的成绩中任意选出个成绩,设事件为“其中个成绩分别属于不同的同学”,求事件发生的概率.
21.(12分) 为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将取得数据整理后,画出频率分布直方图(如图).已知图中从左到右前三个小组的频率分别为,,,第一小组的频数为.
求第四小组的频率;
参加这次测试的学生有多少人;
若次数在次以上(含次)为达标,试估计该年级学生跳绳测试的达标率是多少.
22.(12分) 某家水果店的店长为了解本店苹果的日销售情况,记录了近期连续天苹果的日销售量(单位:),并绘制频率分布直方图如下:
请根据频率分布直方图估计该水果店苹果日销售量的众数和平均数;(同一组中的数据以这组数据所在区间中点的值作代表)
一次进货太多,水果会变得不新鲜;进货太少,又不能满足顾客的需求.店长希望每天的苹果尽量新鲜,又能地满足顾客的需求(在天中,大约有天可以满足顾客的需求),请问每天应该进多少千克苹果?(精确到整数位)
参考答案与试题解析
必修二第九章统计(基础卷)
一、 选择题 (本题共计 12 小题 ,每题 5 分 ,共计60分 )
1.
【答案】
D
【解答】
解:A.总体是名学生的身高,故 A错; B.个体是每一个学生的身高,故B错;
C.样本是,故C错; D.样本容量是,正确。
2.
【答案】
A
【解答】
解:根据题意,结合总体、个体、样本、样本容量的定义可得,
名居民的阅读时间的全体是总体,
故选.
3.
【答案】
B
【解答】
解:样本的平均数为,
方差为,
所以,样本的标准差为.
故选:.
4.
【答案】
C
【解答】
初中部女教师的人数为=;高中部女教师的人数为=,
∴ 该校女教师的人数为=,
5.
【答案】
D
【解答】
解:从随机数表第行的第列和第列数字开始由左到右依次选取两个数字开始向右读,
第一个数为,不符合条件,第二个数为,不符合条件,
第三个数为,符合条件,
以下符合条件依次为:,,,,,
故第个数为.
故选.
6.
【答案】
B
【解答】
解:依据题意,第①项调查中,总体中的个体差异较大,应采用分层抽样法;
第②项调查中,总体中个体较少,应采用简单随机抽样法.
故选.
7.
【答案】
C
【解答】
解:抽出个进行合格检查,发现合格品有个,
则该批产品的合格率为:
.
故选.
8.
【答案】
A
【解答】
解:∵ 在(元)月收入段的频率,
∴ 抽出的人数为:,
选.
9.
【答案】
A
【解答】
解:从随机数表第行的第列和第列数字开始由左到右依次选取两个数字,
分别为:,,,,,,,,,,,,,,
则选出来的前个个体的编号分别为, , ,,,
因此选出来的第个个体的编号为.
故选.
10.
【答案】
C
【解答】
解:从随机数表的倒数第行(表中为随机数表的最后行)第列开始向右读取,
抽取的样本的号码分别是,,,,,,
则抽取的最后一个个体的号码是.
故选.
11.
【答案】
D
【解答】
解:因为学校在校学生人,并且全校参与爬山的人数占总人数的,
所以全校参与爬山的人数为,
所以全校参与跑步的人数为,即.
又因为,
所以.
又因为从中抽取一个人的样本进行调查,
所以高三参与跑步的学生中应抽取的人数为:人.
故选.
12.
【答案】
D
【解答】
解:∵ 用随机数法抽样时,编号的位数应相同,并且不能有负数.
∴ 选项,,均不符合要求,符合要求.
故选.
二、 填空题 (本题共计 4 小题 ,每题 5 分 ,共计20分 )
13.
【答案】
【解答】
解:该医院医生、护士、医技人数之比为,
若医生和护士共抽取了人,
则医生抽取了人,护士抽取了人,医技抽取了人,
所以.
故答案为:.
14.
【答案】
【解答】
解:设录取一本人数为,二本人数为,
由题意可得,
∴ ,,
∴ ,
故答案为:.
15.
【答案】
【解答】
解:∵ 大型超市家、中型超市家、小型超市家,
∴ 共有超市,
∵ 按分层抽样方法抽取一个容量为的样本,
∴ 每个个体被抽到的概率是,
∴ 中型超市要抽取家,
故答案为:.
16.
【答案】
【解答】
观察图表年降水量在范围内有两部分
一部分在,另一部分在
年降水量在范围内应该是,与两部分的概率和
所以年降水量在范围内的概率==
三、 解答题 (本题共计 6 小题 ,共计70分 )
17.
【答案】
由频率分布直方图得:=,解得=.
由频率分布直方图得成绩落在中的频率为=,∴ 估计总体中成绩落在中的学生人数为:=人.
根据频率分布直方图估计名学生数学考试成绩的众位数为:,
设中位数为,则=,则.
【解答】
由频率分布直方图得:=,解得=.
由频率分布直方图得成绩落在中的频率为=,∴ 估计总体中成绩落在中的学生人数为:=人.
根据频率分布直方图估计名学生数学考试成绩的众位数为:,
设中位数为,则=,则.
18.
【答案】
解:(1)为险测产品质量,从流水线上每隔一小时抽取一件产品进行检验,属于系统抽样,
(2)某班分到张电影票,通过抽签的方法确定看电影的同学;属于简单随机抽样,
(3)某小学为了解学生的近视情况,从到年级中按年级学生比例共抽取名学生测量他们的视力,属于分层抽样,
(4)某校在初一招生中,因报名人数超过录取人数,采用摇号的方法产生录取名单,属于随机抽样,
【解答】
解:(1)为险测产品质量,从流水线上每隔一小时抽取一件产品进行检验,属于系统抽样,
(2)某班分到张电影票,通过抽签的方法确定看电影的同学;属于简单随机抽样,
(3)某小学为了解学生的近视情况,从到年级中按年级学生比例共抽取名学生测量他们的视力,属于分层抽样,
(4)某校在初一招生中,因报名人数超过录取人数,采用摇号的方法产生录取名单,属于随机抽样,
19.
【答案】
解:(1)根据频率分布直方图得,年龄在的概率是
,
∴ 年龄在的小矩形图的高是,
把频率分布直方图补充完整即可;
(2)司机年龄位于的频率是,
∴ 对应的司机人数是;
(3)∵ ,
,
设,令,
解得,
∴ 估计该市出租车司机年龄的中位数大约是.
【解答】
解:(1)根据频率分布直方图得,年龄在的概率是
,
∴ 年龄在的小矩形图的高是,
把频率分布直方图补充完整即可;
(2)司机年龄位于的频率是,
∴ 对应的司机人数是;
(3)∵ ,
,
设,令,
解得,
∴ 估计该市出租车司机年龄的中位数大约是.
20.
【答案】
解:由茎叶图知,甲同学成绩的中位数是,
乙同学成绩的中位数是,
乙同学成绩的频率分布直方图如图所示.
从茎叶图可以看出,乙同学成绩的平均值比甲同学成绩的平均值高,乙同学的成绩比甲同学的成绩更稳定.
甲同学不低于分的成绩有个,分别设为,,
乙同学不低于分的成绩有个,分别设为,,,
现从甲、乙两位同学不低于分的成绩中任意选出个成绩,
可能出现的情况有,,,,
,,,,,,共种结果,
其中个成绩分属不同的同学的情况有
,,,,,,共种.
所以事件发生的概率为.
【解答】
解:由茎叶图知,甲同学成绩的中位数是,
乙同学成绩的中位数是,
乙同学成绩的频率分布直方图如图所示.
从茎叶图可以看出,乙同学成绩的平均值比甲同学成绩的平均值高,乙同学的成绩比甲同学的成绩更稳定.
甲同学不低于分的成绩有个,分别设为,,
乙同学不低于分的成绩有个,分别设为,,,
现从甲、乙两位同学不低于分的成绩中任意选出个成绩,
可能出现的情况有,,,,
,,,,,,共种结果,
其中个成绩分属不同的同学的情况有
,,,,,,共种.
所以事件发生的概率为.
21.
【答案】
解:由频率累加和为知,第四小组的频率为:
.
设参加这次测试的学生有人,
则,解得,
即参加这次测试的学生有人.
次数在次以上(含次)的频率为
,
∴ 达标率为.
【解答】
解:由频率累加和为知,第四小组的频率为:
.
设参加这次测试的学生有人,
则,解得,
即参加这次测试的学生有人.
次数在次以上(含次)的频率为
,
∴ 达标率为.
22.
【答案】
解:众数为,
平均数为:
.
日销售量的频率为,
日销量的频率为,
故所求的量位于.
由,
得,
故每天应该进千克苹果.
【解答】
解:众数为,
平均数为:
.
日销售量的频率为,
日销量的频率为,
故所求的量位于.
由,
得,
故每天应该进千克苹果.
试卷第4页,总9页
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 12 小题 ,每题 5 分 ,共计60分 , )
1. 为了了解全校名高一学生的身高情况,从中抽取名学生进行测量.下列说法正确的是( )
A.总体是名 B.个体是每一个学生
C.样本是名学生 D.样本容量是
2. 在“世界读书日”前夕,为了了解某地名居民某天的阅读时间,从中抽取了名居民的阅读时间进行统计分析,在这个问题中,名居民的阅读时间的全体是( )
A.总体 B.个体
C.样本的容量 D.从总体中抽取的一个样本
3. 已知一个样本中的数据为,,,,,则这样的样本标准差为
A. B. C. D.
4. 某中学初中部共有名教师,高中部共有名教师,其性别比例如图所示,则该校女教师的人数为( )
A. B. C. D.
5. 总体由编号为,,…,,的个个体组成.利用下面的随机数表选取个个体,选取方法从随机数表第行的第列和第列数字开始由左到右依次选取两个数字,则选出来的第个个体的编号为( )
A. B. C. D.
6. 某公司在甲、乙、丙、丁四个地区分别有 个、个、 个、 个销售点,公司为了调查产品的销售情况,需从这个销售点中抽取一个容量为的样本,记这项调查为①;在丙地区有个特大型销售点,要从中抽取个销售点调查其销售收入和售后服务等情况,记这项调查为②,则完成①②这两项调查宜采用的抽样方法依次为
A.分层抽样法,系统抽样法
B.分层抽样法,简单随机抽样法
C.系统抽样法,分层抽样法
D.简单随机抽样法,分层抽样法
7. 从某批零件中抽取个,然后再从个中抽出个进行合格检查,发现合格品有个,则该批产品的合格率为( )
A. B. C. D.
8. 一个社会调查机构就某地居民的月收入调查了人,并根据所得数据画了样本的频率分布直方图(如图),为了分析居民的收入与年龄、学历、职业等方面的关系,要从这人中再用分层抽样方法抽出人作进一步调查,则在(元)月收入段应抽出的人数为( )
A. B. C. D.
9. 总体由编号为,,,,的个个体组成,利用下面的随机数表选取个个体,选取方法是从随机数表第行的第列和第列数字开始由左到右依次选取两个数字,则选出来的第个个体的编号为( )
A. B. C. D.
10. 一个总体的个个体的编号分别为,,,,,现需从中抽取一个容量为的样本,请从随机数表的倒数第行(表中为随机数表的最后行)第列开始向右读取,直到取足样本,则抽取的最后一个个体的号码是( )
A. B. C. D.
11. 某学校在校学生人,为了迎接年亚运会,学校举行了亚运会跑步和爬山比赛活动,每人都参加而且只参加其中一项比赛,各年级参与比赛人数情况如下表:
高一级 高二级 高三级
跑步
爬山
其中,全校参与爬山的人数占总人数的.为了了解学生对本次活动的满意程度,从中抽取一个人的样本进行调查,则高三参与跑步的学生中应抽取( )
A.人 B.人 C.人 D.人
12. 从个篮球中任取一个,检查其质量,用随机数法抽取样本,则应编号为
A.,,,,,,,,,
B.,,,,,,,,,
C.,,,,,,,,,
D.,,,,,,,,,
二、 填空题 (本题共计 4 小题 ,每题 5 分 ,共计20分 , )
13. 年初,我国黑龙江省县发现多起新冠肺炎病例.某医院决定派出一支医疗队前往县支援抗疫工作,该医院职工踊跃报名,其中报名的医生人,护士人,医技人,该医院决定采用分层抽样的方法,从中抽取人组成抗疫医疗队,若医生和护士共抽取了人,则________.
14. 某高校招生计划一直在按﹕﹕录取一本、二本、三本新生.若年计划录取的三本人数为人,那么,年录取的二本人数比一本人数多录取的人数为________.
15. 某市有大型超市家、中型超市家、小型超市家.为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为的样本,应抽取中型超市________家.
16. 我国西部一个地区的年降水量在下列区间内的概率如表所示
年降水量
概 率
则年降水量在范围内的概率是________.
三、 解答题 (本题共计 6 小题 ,共计70分 , )
17.(10分) 名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
(1)求频率分布直方图中的值;
(2)估计总体中成绩落在中的学生人数;
(3)根据频率分布直方图估计名学生数学考试成绩的众数,中位数.
18.(12分) 指出下列抽样采用的是哪一种抽样方法?
(1)为险测产品质量,从流水线上每隔一小时抽取一件产品进行检验;
(2)某班分到张电影票,通过抽签的方法确定看电影的同学;
(3)某小学为了解学生的近视情况,从到年级中按年级学生比例共抽取名学生测量他们的视力;
(4)某校在初一招生中,因报名人数超过录取人数,采用摇号的方法产生录取名单.
19.(12分) 某市要对多名出租车司机的年龄进行调查,现从中随机抽出名司机,已知抽到的司机年龄都在岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示.
(1)请你把上述的频率分布直方图补充完整;
(2)司机年龄位于的有多少名?
(3)估计该市出租车司机年龄的中位数大约是多少?
20.(12分) 某中学一教师统计甲、乙两位同学高三学年的数学成绩(满分分),现有甲、乙两位同学的次成绩的茎叶图如图所示.
根据茎叶图求甲、乙两位同学成绩的中位数,并将图中乙同学成绩的频率分布直方图补充完整;
根据茎叶图比较甲、乙两位同学数学成绩的平均值及稳定程度(不要求计算具体值,给出结论即可);
现从甲、乙两位同学不低于分的成绩中任意选出个成绩,设事件为“其中个成绩分别属于不同的同学”,求事件发生的概率.
21.(12分) 为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将取得数据整理后,画出频率分布直方图(如图).已知图中从左到右前三个小组的频率分别为,,,第一小组的频数为.
求第四小组的频率;
参加这次测试的学生有多少人;
若次数在次以上(含次)为达标,试估计该年级学生跳绳测试的达标率是多少.
22.(12分) 某家水果店的店长为了解本店苹果的日销售情况,记录了近期连续天苹果的日销售量(单位:),并绘制频率分布直方图如下:
请根据频率分布直方图估计该水果店苹果日销售量的众数和平均数;(同一组中的数据以这组数据所在区间中点的值作代表)
一次进货太多,水果会变得不新鲜;进货太少,又不能满足顾客的需求.店长希望每天的苹果尽量新鲜,又能地满足顾客的需求(在天中,大约有天可以满足顾客的需求),请问每天应该进多少千克苹果?(精确到整数位)
参考答案与试题解析
必修二第九章统计(基础卷)
一、 选择题 (本题共计 12 小题 ,每题 5 分 ,共计60分 )
1.
【答案】
D
【解答】
解:A.总体是名学生的身高,故 A错; B.个体是每一个学生的身高,故B错;
C.样本是,故C错; D.样本容量是,正确。
2.
【答案】
A
【解答】
解:根据题意,结合总体、个体、样本、样本容量的定义可得,
名居民的阅读时间的全体是总体,
故选.
3.
【答案】
B
【解答】
解:样本的平均数为,
方差为,
所以,样本的标准差为.
故选:.
4.
【答案】
C
【解答】
初中部女教师的人数为=;高中部女教师的人数为=,
∴ 该校女教师的人数为=,
5.
【答案】
D
【解答】
解:从随机数表第行的第列和第列数字开始由左到右依次选取两个数字开始向右读,
第一个数为,不符合条件,第二个数为,不符合条件,
第三个数为,符合条件,
以下符合条件依次为:,,,,,
故第个数为.
故选.
6.
【答案】
B
【解答】
解:依据题意,第①项调查中,总体中的个体差异较大,应采用分层抽样法;
第②项调查中,总体中个体较少,应采用简单随机抽样法.
故选.
7.
【答案】
C
【解答】
解:抽出个进行合格检查,发现合格品有个,
则该批产品的合格率为:
.
故选.
8.
【答案】
A
【解答】
解:∵ 在(元)月收入段的频率,
∴ 抽出的人数为:,
选.
9.
【答案】
A
【解答】
解:从随机数表第行的第列和第列数字开始由左到右依次选取两个数字,
分别为:,,,,,,,,,,,,,,
则选出来的前个个体的编号分别为, , ,,,
因此选出来的第个个体的编号为.
故选.
10.
【答案】
C
【解答】
解:从随机数表的倒数第行(表中为随机数表的最后行)第列开始向右读取,
抽取的样本的号码分别是,,,,,,
则抽取的最后一个个体的号码是.
故选.
11.
【答案】
D
【解答】
解:因为学校在校学生人,并且全校参与爬山的人数占总人数的,
所以全校参与爬山的人数为,
所以全校参与跑步的人数为,即.
又因为,
所以.
又因为从中抽取一个人的样本进行调查,
所以高三参与跑步的学生中应抽取的人数为:人.
故选.
12.
【答案】
D
【解答】
解:∵ 用随机数法抽样时,编号的位数应相同,并且不能有负数.
∴ 选项,,均不符合要求,符合要求.
故选.
二、 填空题 (本题共计 4 小题 ,每题 5 分 ,共计20分 )
13.
【答案】
【解答】
解:该医院医生、护士、医技人数之比为,
若医生和护士共抽取了人,
则医生抽取了人,护士抽取了人,医技抽取了人,
所以.
故答案为:.
14.
【答案】
【解答】
解:设录取一本人数为,二本人数为,
由题意可得,
∴ ,,
∴ ,
故答案为:.
15.
【答案】
【解答】
解:∵ 大型超市家、中型超市家、小型超市家,
∴ 共有超市,
∵ 按分层抽样方法抽取一个容量为的样本,
∴ 每个个体被抽到的概率是,
∴ 中型超市要抽取家,
故答案为:.
16.
【答案】
【解答】
观察图表年降水量在范围内有两部分
一部分在,另一部分在
年降水量在范围内应该是,与两部分的概率和
所以年降水量在范围内的概率==
三、 解答题 (本题共计 6 小题 ,共计70分 )
17.
【答案】
由频率分布直方图得:=,解得=.
由频率分布直方图得成绩落在中的频率为=,∴ 估计总体中成绩落在中的学生人数为:=人.
根据频率分布直方图估计名学生数学考试成绩的众位数为:,
设中位数为,则=,则.
【解答】
由频率分布直方图得:=,解得=.
由频率分布直方图得成绩落在中的频率为=,∴ 估计总体中成绩落在中的学生人数为:=人.
根据频率分布直方图估计名学生数学考试成绩的众位数为:,
设中位数为,则=,则.
18.
【答案】
解:(1)为险测产品质量,从流水线上每隔一小时抽取一件产品进行检验,属于系统抽样,
(2)某班分到张电影票,通过抽签的方法确定看电影的同学;属于简单随机抽样,
(3)某小学为了解学生的近视情况,从到年级中按年级学生比例共抽取名学生测量他们的视力,属于分层抽样,
(4)某校在初一招生中,因报名人数超过录取人数,采用摇号的方法产生录取名单,属于随机抽样,
【解答】
解:(1)为险测产品质量,从流水线上每隔一小时抽取一件产品进行检验,属于系统抽样,
(2)某班分到张电影票,通过抽签的方法确定看电影的同学;属于简单随机抽样,
(3)某小学为了解学生的近视情况,从到年级中按年级学生比例共抽取名学生测量他们的视力,属于分层抽样,
(4)某校在初一招生中,因报名人数超过录取人数,采用摇号的方法产生录取名单,属于随机抽样,
19.
【答案】
解:(1)根据频率分布直方图得,年龄在的概率是
,
∴ 年龄在的小矩形图的高是,
把频率分布直方图补充完整即可;
(2)司机年龄位于的频率是,
∴ 对应的司机人数是;
(3)∵ ,
,
设,令,
解得,
∴ 估计该市出租车司机年龄的中位数大约是.
【解答】
解:(1)根据频率分布直方图得,年龄在的概率是
,
∴ 年龄在的小矩形图的高是,
把频率分布直方图补充完整即可;
(2)司机年龄位于的频率是,
∴ 对应的司机人数是;
(3)∵ ,
,
设,令,
解得,
∴ 估计该市出租车司机年龄的中位数大约是.
20.
【答案】
解:由茎叶图知,甲同学成绩的中位数是,
乙同学成绩的中位数是,
乙同学成绩的频率分布直方图如图所示.
从茎叶图可以看出,乙同学成绩的平均值比甲同学成绩的平均值高,乙同学的成绩比甲同学的成绩更稳定.
甲同学不低于分的成绩有个,分别设为,,
乙同学不低于分的成绩有个,分别设为,,,
现从甲、乙两位同学不低于分的成绩中任意选出个成绩,
可能出现的情况有,,,,
,,,,,,共种结果,
其中个成绩分属不同的同学的情况有
,,,,,,共种.
所以事件发生的概率为.
【解答】
解:由茎叶图知,甲同学成绩的中位数是,
乙同学成绩的中位数是,
乙同学成绩的频率分布直方图如图所示.
从茎叶图可以看出,乙同学成绩的平均值比甲同学成绩的平均值高,乙同学的成绩比甲同学的成绩更稳定.
甲同学不低于分的成绩有个,分别设为,,
乙同学不低于分的成绩有个,分别设为,,,
现从甲、乙两位同学不低于分的成绩中任意选出个成绩,
可能出现的情况有,,,,
,,,,,,共种结果,
其中个成绩分属不同的同学的情况有
,,,,,,共种.
所以事件发生的概率为.
21.
【答案】
解:由频率累加和为知,第四小组的频率为:
.
设参加这次测试的学生有人,
则,解得,
即参加这次测试的学生有人.
次数在次以上(含次)的频率为
,
∴ 达标率为.
【解答】
解:由频率累加和为知,第四小组的频率为:
.
设参加这次测试的学生有人,
则,解得,
即参加这次测试的学生有人.
次数在次以上(含次)的频率为
,
∴ 达标率为.
22.
【答案】
解:众数为,
平均数为:
.
日销售量的频率为,
日销量的频率为,
故所求的量位于.
由,
得,
故每天应该进千克苹果.
【解答】
解:众数为,
平均数为:
.
日销售量的频率为,
日销量的频率为,
故所求的量位于.
由,
得,
故每天应该进千克苹果.
试卷第4页,总9页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
