选择性必修第三册6.1分类加法计数原理与分步乘法计数原理(Word版含解析)
文档属性
| 名称 | 选择性必修第三册6.1分类加法计数原理与分步乘法计数原理(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 09:23:37 | ||
图片预览




文档简介
选择性必修第三册 6.1分类加法计数原理与分步乘法计数原理
一、单选题
1.数学中有回文数,如343,12521等.两位数的回文数有11,22,33,…,99,共9个,则在三位数的回文数中偶数的个数是( )
A.40 B.30 C.20 D.10
2.用黑白两种颜色随机地染如图所示表格中6个格子,每个格子染一种颜色,并且从左到右数,不管数到哪个格子,总有黑色格子不少于白色格 的染色方法种数为( )
A.15 B.16 C.18 D.20
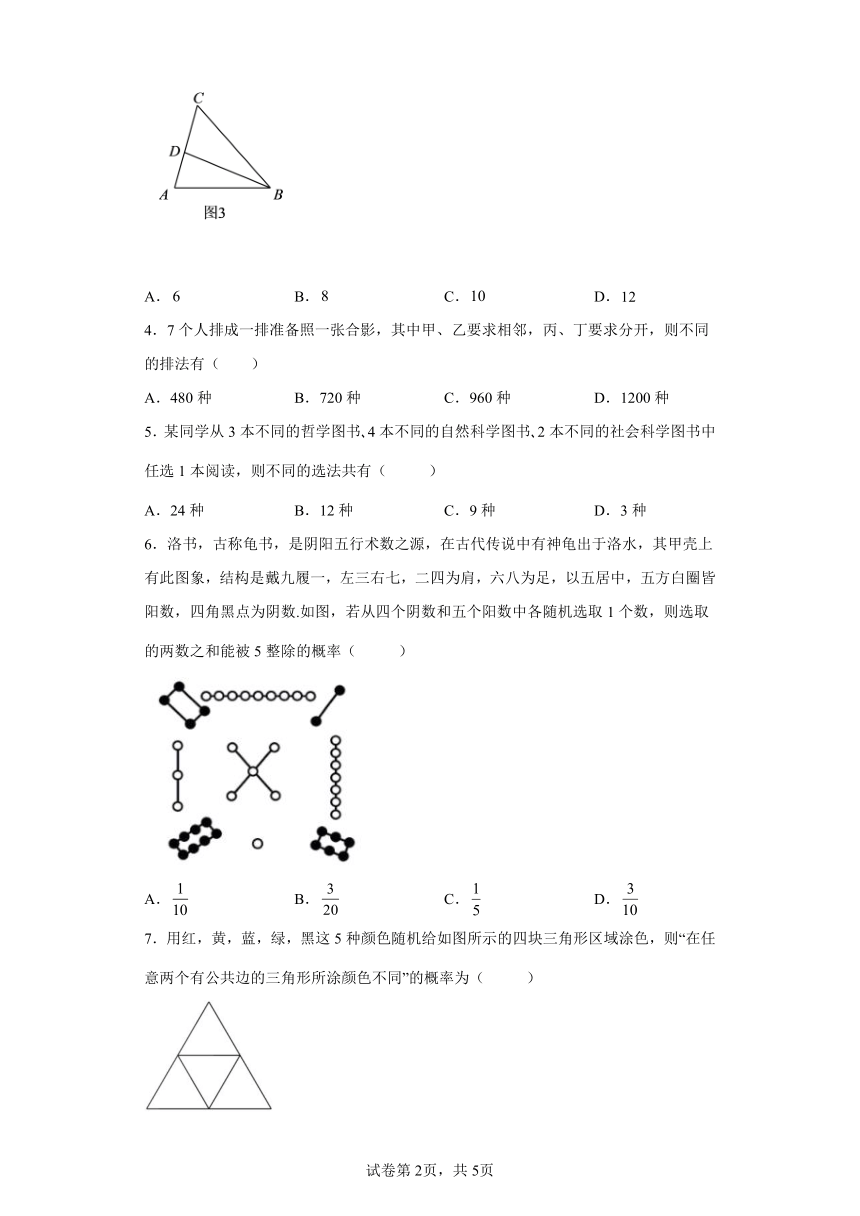
3.十八世纪初普鲁士的哥尼斯堡,有一条河穿过,河上有两个小岛,有七座桥把两个岛与河岸连接起来.有人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完这七座桥,最后回到出发点.这就是著名的哥尼斯堡七桥问题(下简称七桥问题),很多人尝试解决这个问题,但绞尽脑汁,就是无法找到答案.直到1736年,29岁的欧拉以拉丁文正式发表了论文《关于位置几何问题的解法》,文中详细讨论了七桥问题并作了一些推广,该论文被认为是图论、拓扑学和网络科学的发端.图1是欧拉当年解决七桥问题的手绘图,图2是该问题相应的示意图,其中,,,四个点代表陆地,连接这些点的边就是桥.欧拉将七桥问题转化成一个几何问题——笔画问题.一笔画问题中,要求不遗漏地依次走完每一条边,允许重复走过某些结点,可以不回到出发点,但不允许重复走过任何一条边.在图3中,根据以上一笔画问题的规则,不同的走法总数为( )
A. B. C. D.
4.7个人排成一排准备照一张合影,其中甲、乙要求相邻,丙、丁要求分开,则不同的排法有( )
A.480种 B.720种 C.960种 D.1200种
5.某同学从3本不同的哲学图书 4本不同的自然科学图书 2本不同的社会科学图书中任选1本阅读,则不同的选法共有( )
A.24种 B.12种 C.9种 D.3种
6.洛书,古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有此图象,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四角黑点为阴数.如图,若从四个阴数和五个阳数中各随机选取1个数,则选取的两数之和能被5整除的概率( )
A. B. C. D.
7.用红,黄,蓝,绿,黑这5种颜色随机给如图所示的四块三角形区域涂色,则“在任意两个有公共边的三角形所涂颜色不同”的概率为( )
A. B. C. D.
8.中国代表团在2022年北京冬奥会获得九枚金牌,其中雪上项目金牌为5枚,冰上项目金牌为4枚.现有6名同学要报名参加冰雪兴趣小组,要求雪上项目和冰上项目都至少有2人参加,则不同的报名方案有( )
A.35 B.50 C.70 D.100
9.第七届世界军运会于2019年10月18日至27日在中国武汉举行.某电视台在19日至24日六天中共有7场直播(如下表所示),张三打算选取其中的三场观看.则观看的任意两场直播中间至少间隔一天(如第一场19日观看直播则20日不能观看直播)的概率是( )
日期 19日 20日 21日 22日 23日 24日
时间 全天 全天 上午 下午 全天 全天 全天
内容 飞行比赛 击剑 射击 游泳 篮球 定向越野 障碍跑
A. B. C. D.
10.某夜市的一排摊位上共有9个铺位,现有6家小吃类店铺,3家饮料类店铺打算入驻,若要排出一个摊位规划,要求饮料类店铺不能相邻,则可以排出的摊位规划总个数为( )
A. B. C. D.
11.作家马伯庸的小说《长安十二时辰》中,靖安司通过长安城内的望楼传递信息.如图所示是望楼传递信息的一种方式,在九宫格中,每个小方格可以在白色和紫色(此处以阴影代表紫色)之间变换,从而一共可以有512种不同的颜色组合,即代表512种不同的信息.现要求每一行、每一列上有且只有1个紫色小方格(如图所示即满足要求),则一共可以传递的不同信息种数是( )
A.14 B.12 C.9 D.6
12.如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供6种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色、相邻颜色不同,则区域不同涂色的方法种数为( )
A.420 B.960 C.1440 D.1560
二、填空题
13.楼道里有12盏灯,为了节约用电,需关掉3盏不相邻的灯,则关灯方案有______种.
14.5名同学去听同时举行的3个课外知识讲座,每名同学可自由选择听其中的1个讲座,不同选择的种数是________;
15.将摆放在编号为五个位置上的件不同商品重新摆放,则恰有一件商品的位置不变的摆放方法数为_________.(用数字作答)
16.今有2只红球、3只黄球,同色球不加以区分,将这5只球排成一列,有______种不同的方法(用数字作答).
17.如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供4种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻颜色不同,则不同的涂色方法种数为____________.
三、解答题
18.有6张分别标有数字1,2,3,4,5,6的卡片,将其排成3行2列,要求每一行的两张卡片上的数字之和均不等于7,求不同的排法种数.
19.某电视台连续播放6个广告,其中有3个商业广告、2个宣传广告和1个公益广告,要求最后播放的不能是商业广告,宣传广告与公益广告不能连续播放,2个宣传广告也不能连续播放,则有多少种不同的播放方式?
20.已知集合,表示平面上的点,问:
(1)P可表示平面上多少个第二象限的点?
(2)P可表示多少个不在直线上的点?
21.已知某种新产品的编号由1个英文字母和1个数字组合而成,且英文字母在前.其中英文字母可以是A,B,C,D,E,F这6个字母中的1个,数字可以是1,2,…,9这9个数字中的1个.问:共有多少种不同的编号?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
首先安排末(首)位,再考虑中间位置,按照分步乘法计数原理计算可得;
【详解】
解:由题意,若三位数的回文数是偶数,则末(首)位可能为2,4,6,8.如果末(首)位为2,中间一位数有10种可能,同理可得,如果末(首)位为4或6或8,中间一位数均有10种可能,所以在三位数的回文数总偶数的个数是.
故选:A
2.D
根据题意,分情况讨论,求出每种情况对应的染色方法种数,即可得出结果.
【详解】
依题意,第一个格子必须为黑色,设格子从左到右的编号分别为1~6.
故①当1,3,5号格子为黑色时:有23=8种;
②当1,3号为黑色且5号为白色时:若2号为黑色则有22=4种,若2号为白色,则4号为黑色有2种,故此时共有4+2=6种;
③当1号为黑色,3号为白色时:2号必为黑色,若4号为白色,则有1×1×1×1×1×2=2种,若4号为黑色,则有1×1×1×1×2×2=4种,故此时共有2+4=6种;
综上,共有8+6+6=20种.
故选:D.
本题主要考查排列组合,意在考查考生的化归与转化能力、运算求解能力、逻辑推理能力,考查的核心素养是数学运算、逻辑推理.本题解题的关键在于对1,3,5号格子的颜色进行讨论求解.
3.D
根据欧拉找到的“一笔画”规律:凡是只有两个奇点的连通图(其余都为偶点)一定可以一笔画成.画时必须把一个奇点为起点,另一个奇点为终点.
【详解】
图中,和是偶点,和是奇点,根据欧拉找到的“一笔画”规律:凡是只有两个奇点的连通图(其余都为偶点)一定可以一笔画成.画时必须把一个奇点为起点,另一个奇点为终点.
以为起点时,有、、、、、六种画法
以为起点时,所有路线与以上情况相反即可,也有六种,故共有种画法
故选:D
4.C
甲、乙要求相邻,则把甲和乙看成一个元素,与除去丙和丁以外的共4个元素进行全排列,其中甲和乙之间还有一个排列,根据丙和丁不相邻,把形成的五个空选两个排列丙和丁.得到结果.
【详解】
解:由题意知,
甲、乙要求相邻,则把甲和乙看成一个元素,
与除去丙和丁以外的共4个元素进行全排列,其中甲和乙之间还有一个排列,
把形成的五个空选两个排列丙和丁,
根据分步计数原理知共有A44A22A52=960种.
故选:C.
5.C
利用分类加法计数原理直接求出答案即可.
【详解】
解:由分类加法计数原理知,不同的选法种数为.
故选:C.
6.C
由题意可知,阴数为2,4,6,8,阳数为1,3,5,7,9. 各选一个数,求出所有的选法,求出其和能被5整除的选法种数,根据古典概型的概率计算公式,即得答案.
【详解】
由题意可知,阴数为2,4,6,8,阳数为1,3,5,7,9.
各选一个数,共有种选法.
其和能被5整除的分别为:2,3;4,1;6,9;8,7,共4种选法,
选取的两数之和能被5整除的概率.
故选:C.
本题考查古典概型和计数原理,属于基础题.
7.A
求出所有涂色方法数为,再求出在任意两个有公共边的三角形所涂颜色不同的方法数,可先从中间一个三角形涂色,然后再涂其他三个三角形.
【详解】
5种颜色随机给如图所示的四块三角形区域涂色方法数为,
有公共边的三角形为同色,先考虑中间一块涂色有5种方法,其他三个三角形在剩下的4色中任意涂色均可,方法为,
所以所求概率为.
故选:A.
8.B
根据要求雪上项目和冰上项目都至少有2人参加,可将6名同学分为和两类,通过分步乘法计数原理,分别求出每一类组合有多少种,再由分类加法计数原理可得答案.
【详解】
由题干可知,要求雪上项目和冰上项目都至少有2人参加,则组合为:和两类,
(1)若为“”组合,将6名同学分为两组,一组2人,另一组4人,有种分组方式;将分好的2组在雪上项目和冰上项目进行全排列有种,由分步乘法计数原理,则该组合有种;
(2)若为“”组合将6名同学分为两组,一组3人,另一组也为3人,有种分组方式,将分好的2组在雪上项目和冰上项目进行全排列有种,由分步乘法计数原理,则该组合有种;
由分类加法计数原理,则不同的报名方式有种;
故选:B.
9.B
先求出场直播中任意选取三场的种数,再计算选取的三场任意两场直播中间至少间隔一天的种数,利用概率除法公式即可求解.
【详解】
从场直播中任意选取三场有种,
三场任意两场直播中间至少间隔一天有四类:
选取日,有种,
选取日,有种,
选取日,有1种,
选取日,有1种,
所以选取的三场任意两场直播中间至少间隔一天的有种,
所以概率为,
故选:B
关键点点睛:本体的关键是准确求出场直播中任意选取三场的种数,以及选取的三场任意两场直播中间至少间隔一天的种数,理解分类加法与分步乘法的区别.
10.D
不相邻问题用插空法,先排好小吃类店铺,然后将饮料类店铺进行插空即可.
【详解】
先将6个小吃类店铺进行全排列,有种排法,再从这6个小吃类店铺形成的7个空中选3个进行排列,有种排法,故排出的摊位规划总个数为.
故选:D
11.D
由分步乘法原理求传递的不同信息种数.
【详解】
根据每行中紫色小方格的位置,可分三步:第一步,在第一行中,有且只有1个紫色小方格,有3种情况;第二步,在第二行的3个方格中,要求每列有且只有1个紫色小方格,则第二行有2种情况;第三步,在第三行,只有1种情况,则一共可以传递的信息种数是,
故选:D.
12.D
根据题意,分4步依次分析区域、、、、的涂色方法数目,由分步计数原理计算答案.
【详解】
解:分4步进行分析:
①,对于区域,有6种颜色可选;
②,对于区域,与区域相邻,有5种颜色可选;
③,对于区域,与、区域相邻,有4种颜色可选;
④,对于区域、,若与颜色相同,区域有4种颜色可选,
若与颜色不相同,区域有3种颜色可选,区域有3种颜色可选,
则区域、有种选择,
则不同的涂色方案有种;
故选:D
13.210
分3个中任意2个都不相邻,由9盏亮灯的10个空隙中插入3个,有两个相邻时,把2个相邻的捆绑在一起,由9盏亮灯的10个空隙中插入2个,然后利用分类计数原理求解.
【详解】
当3个中任意2个都不相邻时,把此问题当作一个排队模型在9盏亮灯的10个空隙中插入3个不亮的灯有=120种.
当有两个相邻时,把2个相邻的捆绑在一起,和上面的做法一样,9盏亮灯的10个空隙中插入2个有,
共有120+90=210种.
故答案为:210
14.243
根据题意,分析出每位同学有3种选择,进而由分步乘法计数原理可得答案.
【详解】
根据题意,每名同学可自由选择听3个讲座中的任意一个,所以每位同学有3种选择方法,
所以5名同学共有种选择方法.
故答案为:.
15.45
先选出件,放回原来的位置,有5种,再将剩下的四件都不在原来位置.
【详解】
根据题意,分步进行分析:
(1)将件不同商品中选出件,放回原来的位置,有种情况,假设编号为的位置不变,
(2)剩下四件都不在原来位置,即编号为的四件商品都不在原来位置,
编号为的商品有种放法,假设其放在了号商品原来的位置,则号商品有种放法,
剩下编号为3,4的两件商品只有种放法,
则其余四件商品的放法有种,
故恰有一件商品的位置不变的摆放方法有种,
故答案为:45.
16.10
由分步计数原理可分两步完成,第一步:在5个不同位置中选2个位置排红球, 第二步:在剩下的3个不同位置排黄球,再运算即可得解.
【详解】
分两步完成,
第一步:在5个不同位置中选2个位置排红球,共种排法,
第二步:在剩下的3个不同位置排黄球,共种排法,
故将这5只球排成一列,有种不同的方法,
故答案为:10.
17.72
根据题意,分4步依次分析区域、、、、的涂色方法数目,由分步计数原理计算答案.
【详解】
分4步进行分析:
①,对于区域,有4种颜色可选;
②,对于区域,与区域相邻,有3种颜色可选;
③,对于区域,与、区域相邻,有2种颜色可选;
④,对于区域、,若与颜色相同,区域有2种颜色可选,
若与颜色不相同,区域有1种颜色可选,区域有1种颜色可选,
则区域、有种选择,
则不同的涂色方案有种;
故答案为:72
18.384(种)
等于7的数字可分成三组:,,,第一行的排法种数为种,第二行的排法种数为种,第三行有2种排法,由分步乘法计数原理即得解
【详解】
将1,2,3,4,5,6中数字之和等于7的两个数字分成一组,
记,,.
第一步,排第一行的两个数字,先从,,三组中选取两组,有3种选法,再从这两组中各选取一个数,有种选法,最后将这两个数排在第一行,有2种排法,故第一行的排法种数为.
第二步,排第二行的两个数字,先从,,中第一步未选到的那一组中选取一个数,有2种选法,再从第一步选取的两组中剩余的两个数中选取一个数,有2种选法,最后将这两个数排在第二行,有2种排法,故第二行的排法种数为.
第三步,将余下的两个数排在第三行,有2种排法.
由分步乘法计数原理,知不同的排法共有(种).
19.108种
结合分类加法、分步乘法计数原理计算出正确答案.
【详解】
用1,2,3,4,5,6表示广告的播放顺序,则完成这件事有3类方法.
第1类,宣传广告与公益广告的播放顺序是2,4,6.分6步完成这件事,共有种不同的播放方式;
第2类,宣传广告与公益广告的播放顺序是1,4,6.分6步完成这件事,共有种不同的播放方式;
第3类,宣传广告与公益广告的播放顺序是1,3,6.同样分6步完成这件事,共有种不同的播放方式,
由分类加法计数原理,得6个广告不同的播放方式共有种.
20.(1)6(个);(2)30(个).
(1)由分步乘法原理求第二象限的点的个数,(2)依次确定横坐标和纵坐标的可能取法,由分步乘法原理求不在直线上的点的个数.
【详解】
(1)因为P表示平面上第二象限的点,故可分两步:
第一步,确定a,a必须小于0,则有3种不同的情况;
第二步,确定b,b必须大于0,则有2种不同的情况;
根据分步乘法计数原理,第二象限的点共有(个).
(2)因为P表示不在直线上的点,故可分两步:
第一步,确定a,有6种不同的情况;
第二步,确定b,有5种不同的情况.
根据分步乘法计数原理,不在直线上的点共有(个).
21.54
利用分步相乘计数原理即可得解.
【详解】
根据题意,完成编号分两步完成:
第1步,从6个英文字母中选1个,有6种方法;
第2步,从9个数字中选1个,有9种方法;
根据分步乘法计数原理,不同取法的种数为.
所以共有54种不同的编号.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.数学中有回文数,如343,12521等.两位数的回文数有11,22,33,…,99,共9个,则在三位数的回文数中偶数的个数是( )
A.40 B.30 C.20 D.10
2.用黑白两种颜色随机地染如图所示表格中6个格子,每个格子染一种颜色,并且从左到右数,不管数到哪个格子,总有黑色格子不少于白色格 的染色方法种数为( )
A.15 B.16 C.18 D.20
3.十八世纪初普鲁士的哥尼斯堡,有一条河穿过,河上有两个小岛,有七座桥把两个岛与河岸连接起来.有人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完这七座桥,最后回到出发点.这就是著名的哥尼斯堡七桥问题(下简称七桥问题),很多人尝试解决这个问题,但绞尽脑汁,就是无法找到答案.直到1736年,29岁的欧拉以拉丁文正式发表了论文《关于位置几何问题的解法》,文中详细讨论了七桥问题并作了一些推广,该论文被认为是图论、拓扑学和网络科学的发端.图1是欧拉当年解决七桥问题的手绘图,图2是该问题相应的示意图,其中,,,四个点代表陆地,连接这些点的边就是桥.欧拉将七桥问题转化成一个几何问题——笔画问题.一笔画问题中,要求不遗漏地依次走完每一条边,允许重复走过某些结点,可以不回到出发点,但不允许重复走过任何一条边.在图3中,根据以上一笔画问题的规则,不同的走法总数为( )
A. B. C. D.
4.7个人排成一排准备照一张合影,其中甲、乙要求相邻,丙、丁要求分开,则不同的排法有( )
A.480种 B.720种 C.960种 D.1200种
5.某同学从3本不同的哲学图书 4本不同的自然科学图书 2本不同的社会科学图书中任选1本阅读,则不同的选法共有( )
A.24种 B.12种 C.9种 D.3种
6.洛书,古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有此图象,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四角黑点为阴数.如图,若从四个阴数和五个阳数中各随机选取1个数,则选取的两数之和能被5整除的概率( )
A. B. C. D.
7.用红,黄,蓝,绿,黑这5种颜色随机给如图所示的四块三角形区域涂色,则“在任意两个有公共边的三角形所涂颜色不同”的概率为( )
A. B. C. D.
8.中国代表团在2022年北京冬奥会获得九枚金牌,其中雪上项目金牌为5枚,冰上项目金牌为4枚.现有6名同学要报名参加冰雪兴趣小组,要求雪上项目和冰上项目都至少有2人参加,则不同的报名方案有( )
A.35 B.50 C.70 D.100
9.第七届世界军运会于2019年10月18日至27日在中国武汉举行.某电视台在19日至24日六天中共有7场直播(如下表所示),张三打算选取其中的三场观看.则观看的任意两场直播中间至少间隔一天(如第一场19日观看直播则20日不能观看直播)的概率是( )
日期 19日 20日 21日 22日 23日 24日
时间 全天 全天 上午 下午 全天 全天 全天
内容 飞行比赛 击剑 射击 游泳 篮球 定向越野 障碍跑
A. B. C. D.
10.某夜市的一排摊位上共有9个铺位,现有6家小吃类店铺,3家饮料类店铺打算入驻,若要排出一个摊位规划,要求饮料类店铺不能相邻,则可以排出的摊位规划总个数为( )
A. B. C. D.
11.作家马伯庸的小说《长安十二时辰》中,靖安司通过长安城内的望楼传递信息.如图所示是望楼传递信息的一种方式,在九宫格中,每个小方格可以在白色和紫色(此处以阴影代表紫色)之间变换,从而一共可以有512种不同的颜色组合,即代表512种不同的信息.现要求每一行、每一列上有且只有1个紫色小方格(如图所示即满足要求),则一共可以传递的不同信息种数是( )
A.14 B.12 C.9 D.6
12.如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供6种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色、相邻颜色不同,则区域不同涂色的方法种数为( )
A.420 B.960 C.1440 D.1560
二、填空题
13.楼道里有12盏灯,为了节约用电,需关掉3盏不相邻的灯,则关灯方案有______种.
14.5名同学去听同时举行的3个课外知识讲座,每名同学可自由选择听其中的1个讲座,不同选择的种数是________;
15.将摆放在编号为五个位置上的件不同商品重新摆放,则恰有一件商品的位置不变的摆放方法数为_________.(用数字作答)
16.今有2只红球、3只黄球,同色球不加以区分,将这5只球排成一列,有______种不同的方法(用数字作答).
17.如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供4种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻颜色不同,则不同的涂色方法种数为____________.
三、解答题
18.有6张分别标有数字1,2,3,4,5,6的卡片,将其排成3行2列,要求每一行的两张卡片上的数字之和均不等于7,求不同的排法种数.
19.某电视台连续播放6个广告,其中有3个商业广告、2个宣传广告和1个公益广告,要求最后播放的不能是商业广告,宣传广告与公益广告不能连续播放,2个宣传广告也不能连续播放,则有多少种不同的播放方式?
20.已知集合,表示平面上的点,问:
(1)P可表示平面上多少个第二象限的点?
(2)P可表示多少个不在直线上的点?
21.已知某种新产品的编号由1个英文字母和1个数字组合而成,且英文字母在前.其中英文字母可以是A,B,C,D,E,F这6个字母中的1个,数字可以是1,2,…,9这9个数字中的1个.问:共有多少种不同的编号?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
首先安排末(首)位,再考虑中间位置,按照分步乘法计数原理计算可得;
【详解】
解:由题意,若三位数的回文数是偶数,则末(首)位可能为2,4,6,8.如果末(首)位为2,中间一位数有10种可能,同理可得,如果末(首)位为4或6或8,中间一位数均有10种可能,所以在三位数的回文数总偶数的个数是.
故选:A
2.D
根据题意,分情况讨论,求出每种情况对应的染色方法种数,即可得出结果.
【详解】
依题意,第一个格子必须为黑色,设格子从左到右的编号分别为1~6.
故①当1,3,5号格子为黑色时:有23=8种;
②当1,3号为黑色且5号为白色时:若2号为黑色则有22=4种,若2号为白色,则4号为黑色有2种,故此时共有4+2=6种;
③当1号为黑色,3号为白色时:2号必为黑色,若4号为白色,则有1×1×1×1×1×2=2种,若4号为黑色,则有1×1×1×1×2×2=4种,故此时共有2+4=6种;
综上,共有8+6+6=20种.
故选:D.
本题主要考查排列组合,意在考查考生的化归与转化能力、运算求解能力、逻辑推理能力,考查的核心素养是数学运算、逻辑推理.本题解题的关键在于对1,3,5号格子的颜色进行讨论求解.
3.D
根据欧拉找到的“一笔画”规律:凡是只有两个奇点的连通图(其余都为偶点)一定可以一笔画成.画时必须把一个奇点为起点,另一个奇点为终点.
【详解】
图中,和是偶点,和是奇点,根据欧拉找到的“一笔画”规律:凡是只有两个奇点的连通图(其余都为偶点)一定可以一笔画成.画时必须把一个奇点为起点,另一个奇点为终点.
以为起点时,有、、、、、六种画法
以为起点时,所有路线与以上情况相反即可,也有六种,故共有种画法
故选:D
4.C
甲、乙要求相邻,则把甲和乙看成一个元素,与除去丙和丁以外的共4个元素进行全排列,其中甲和乙之间还有一个排列,根据丙和丁不相邻,把形成的五个空选两个排列丙和丁.得到结果.
【详解】
解:由题意知,
甲、乙要求相邻,则把甲和乙看成一个元素,
与除去丙和丁以外的共4个元素进行全排列,其中甲和乙之间还有一个排列,
把形成的五个空选两个排列丙和丁,
根据分步计数原理知共有A44A22A52=960种.
故选:C.
5.C
利用分类加法计数原理直接求出答案即可.
【详解】
解:由分类加法计数原理知,不同的选法种数为.
故选:C.
6.C
由题意可知,阴数为2,4,6,8,阳数为1,3,5,7,9. 各选一个数,求出所有的选法,求出其和能被5整除的选法种数,根据古典概型的概率计算公式,即得答案.
【详解】
由题意可知,阴数为2,4,6,8,阳数为1,3,5,7,9.
各选一个数,共有种选法.
其和能被5整除的分别为:2,3;4,1;6,9;8,7,共4种选法,
选取的两数之和能被5整除的概率.
故选:C.
本题考查古典概型和计数原理,属于基础题.
7.A
求出所有涂色方法数为,再求出在任意两个有公共边的三角形所涂颜色不同的方法数,可先从中间一个三角形涂色,然后再涂其他三个三角形.
【详解】
5种颜色随机给如图所示的四块三角形区域涂色方法数为,
有公共边的三角形为同色,先考虑中间一块涂色有5种方法,其他三个三角形在剩下的4色中任意涂色均可,方法为,
所以所求概率为.
故选:A.
8.B
根据要求雪上项目和冰上项目都至少有2人参加,可将6名同学分为和两类,通过分步乘法计数原理,分别求出每一类组合有多少种,再由分类加法计数原理可得答案.
【详解】
由题干可知,要求雪上项目和冰上项目都至少有2人参加,则组合为:和两类,
(1)若为“”组合,将6名同学分为两组,一组2人,另一组4人,有种分组方式;将分好的2组在雪上项目和冰上项目进行全排列有种,由分步乘法计数原理,则该组合有种;
(2)若为“”组合将6名同学分为两组,一组3人,另一组也为3人,有种分组方式,将分好的2组在雪上项目和冰上项目进行全排列有种,由分步乘法计数原理,则该组合有种;
由分类加法计数原理,则不同的报名方式有种;
故选:B.
9.B
先求出场直播中任意选取三场的种数,再计算选取的三场任意两场直播中间至少间隔一天的种数,利用概率除法公式即可求解.
【详解】
从场直播中任意选取三场有种,
三场任意两场直播中间至少间隔一天有四类:
选取日,有种,
选取日,有种,
选取日,有1种,
选取日,有1种,
所以选取的三场任意两场直播中间至少间隔一天的有种,
所以概率为,
故选:B
关键点点睛:本体的关键是准确求出场直播中任意选取三场的种数,以及选取的三场任意两场直播中间至少间隔一天的种数,理解分类加法与分步乘法的区别.
10.D
不相邻问题用插空法,先排好小吃类店铺,然后将饮料类店铺进行插空即可.
【详解】
先将6个小吃类店铺进行全排列,有种排法,再从这6个小吃类店铺形成的7个空中选3个进行排列,有种排法,故排出的摊位规划总个数为.
故选:D
11.D
由分步乘法原理求传递的不同信息种数.
【详解】
根据每行中紫色小方格的位置,可分三步:第一步,在第一行中,有且只有1个紫色小方格,有3种情况;第二步,在第二行的3个方格中,要求每列有且只有1个紫色小方格,则第二行有2种情况;第三步,在第三行,只有1种情况,则一共可以传递的信息种数是,
故选:D.
12.D
根据题意,分4步依次分析区域、、、、的涂色方法数目,由分步计数原理计算答案.
【详解】
解:分4步进行分析:
①,对于区域,有6种颜色可选;
②,对于区域,与区域相邻,有5种颜色可选;
③,对于区域,与、区域相邻,有4种颜色可选;
④,对于区域、,若与颜色相同,区域有4种颜色可选,
若与颜色不相同,区域有3种颜色可选,区域有3种颜色可选,
则区域、有种选择,
则不同的涂色方案有种;
故选:D
13.210
分3个中任意2个都不相邻,由9盏亮灯的10个空隙中插入3个,有两个相邻时,把2个相邻的捆绑在一起,由9盏亮灯的10个空隙中插入2个,然后利用分类计数原理求解.
【详解】
当3个中任意2个都不相邻时,把此问题当作一个排队模型在9盏亮灯的10个空隙中插入3个不亮的灯有=120种.
当有两个相邻时,把2个相邻的捆绑在一起,和上面的做法一样,9盏亮灯的10个空隙中插入2个有,
共有120+90=210种.
故答案为:210
14.243
根据题意,分析出每位同学有3种选择,进而由分步乘法计数原理可得答案.
【详解】
根据题意,每名同学可自由选择听3个讲座中的任意一个,所以每位同学有3种选择方法,
所以5名同学共有种选择方法.
故答案为:.
15.45
先选出件,放回原来的位置,有5种,再将剩下的四件都不在原来位置.
【详解】
根据题意,分步进行分析:
(1)将件不同商品中选出件,放回原来的位置,有种情况,假设编号为的位置不变,
(2)剩下四件都不在原来位置,即编号为的四件商品都不在原来位置,
编号为的商品有种放法,假设其放在了号商品原来的位置,则号商品有种放法,
剩下编号为3,4的两件商品只有种放法,
则其余四件商品的放法有种,
故恰有一件商品的位置不变的摆放方法有种,
故答案为:45.
16.10
由分步计数原理可分两步完成,第一步:在5个不同位置中选2个位置排红球, 第二步:在剩下的3个不同位置排黄球,再运算即可得解.
【详解】
分两步完成,
第一步:在5个不同位置中选2个位置排红球,共种排法,
第二步:在剩下的3个不同位置排黄球,共种排法,
故将这5只球排成一列,有种不同的方法,
故答案为:10.
17.72
根据题意,分4步依次分析区域、、、、的涂色方法数目,由分步计数原理计算答案.
【详解】
分4步进行分析:
①,对于区域,有4种颜色可选;
②,对于区域,与区域相邻,有3种颜色可选;
③,对于区域,与、区域相邻,有2种颜色可选;
④,对于区域、,若与颜色相同,区域有2种颜色可选,
若与颜色不相同,区域有1种颜色可选,区域有1种颜色可选,
则区域、有种选择,
则不同的涂色方案有种;
故答案为:72
18.384(种)
等于7的数字可分成三组:,,,第一行的排法种数为种,第二行的排法种数为种,第三行有2种排法,由分步乘法计数原理即得解
【详解】
将1,2,3,4,5,6中数字之和等于7的两个数字分成一组,
记,,.
第一步,排第一行的两个数字,先从,,三组中选取两组,有3种选法,再从这两组中各选取一个数,有种选法,最后将这两个数排在第一行,有2种排法,故第一行的排法种数为.
第二步,排第二行的两个数字,先从,,中第一步未选到的那一组中选取一个数,有2种选法,再从第一步选取的两组中剩余的两个数中选取一个数,有2种选法,最后将这两个数排在第二行,有2种排法,故第二行的排法种数为.
第三步,将余下的两个数排在第三行,有2种排法.
由分步乘法计数原理,知不同的排法共有(种).
19.108种
结合分类加法、分步乘法计数原理计算出正确答案.
【详解】
用1,2,3,4,5,6表示广告的播放顺序,则完成这件事有3类方法.
第1类,宣传广告与公益广告的播放顺序是2,4,6.分6步完成这件事,共有种不同的播放方式;
第2类,宣传广告与公益广告的播放顺序是1,4,6.分6步完成这件事,共有种不同的播放方式;
第3类,宣传广告与公益广告的播放顺序是1,3,6.同样分6步完成这件事,共有种不同的播放方式,
由分类加法计数原理,得6个广告不同的播放方式共有种.
20.(1)6(个);(2)30(个).
(1)由分步乘法原理求第二象限的点的个数,(2)依次确定横坐标和纵坐标的可能取法,由分步乘法原理求不在直线上的点的个数.
【详解】
(1)因为P表示平面上第二象限的点,故可分两步:
第一步,确定a,a必须小于0,则有3种不同的情况;
第二步,确定b,b必须大于0,则有2种不同的情况;
根据分步乘法计数原理,第二象限的点共有(个).
(2)因为P表示不在直线上的点,故可分两步:
第一步,确定a,有6种不同的情况;
第二步,确定b,有5种不同的情况.
根据分步乘法计数原理,不在直线上的点共有(个).
21.54
利用分步相乘计数原理即可得解.
【详解】
根据题意,完成编号分两步完成:
第1步,从6个英文字母中选1个,有6种方法;
第2步,从9个数字中选1个,有9种方法;
根据分步乘法计数原理,不同取法的种数为.
所以共有54种不同的编号.
答案第1页,共2页
答案第1页,共2页
