北京版八年级数学上册12.5 全等三角形的实际应用 教学设计(表格式)
文档属性
| 名称 | 北京版八年级数学上册12.5 全等三角形的实际应用 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 487.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-25 04:43:29 | ||
图片预览


文档简介
任课教师 授课年级 初二 授课日期
教学课题 全等三角形的实际应用
教学目标 1.让学生进一步巩固判定三角形全等的方法,培养学生的理性思考和逻辑推理能力; 2.让学生经历构造全等三角形解决实际问题的过程,培养学生的数学建模能力和语言表达能力; 3.让学生感受数学与实际的广泛、密切联系,体会数学说理的严谨、数学应用的价值,激发学生学习的兴趣和信心.
教学方法 小组合作学习
教学重点 已知一个三角形利用中点,平行线构建一个与其全等的三角形
教学难点 从实际问题中抽象出几何模形(三角形),进而构建全等三角形
教学过程 作业展示——小组探究——小组展示——我的收获
教 学 内 容 学生活动 教学意图
一、独立完成 1.如图1所示,AC和BD相较于点O,且OA=OC 请你添加一个条件使△ABO≌△CDO,并说明理由. 已知条件:OA=OC 隐含条件:∠AOB=∠COD(对顶角) 回答问题 回忆三角形全等的判定定理—可用于间接测量长度、距离的SAS、ASA (AAS),
学科 第 课时
教 学 内 容 学生活动 教学意图
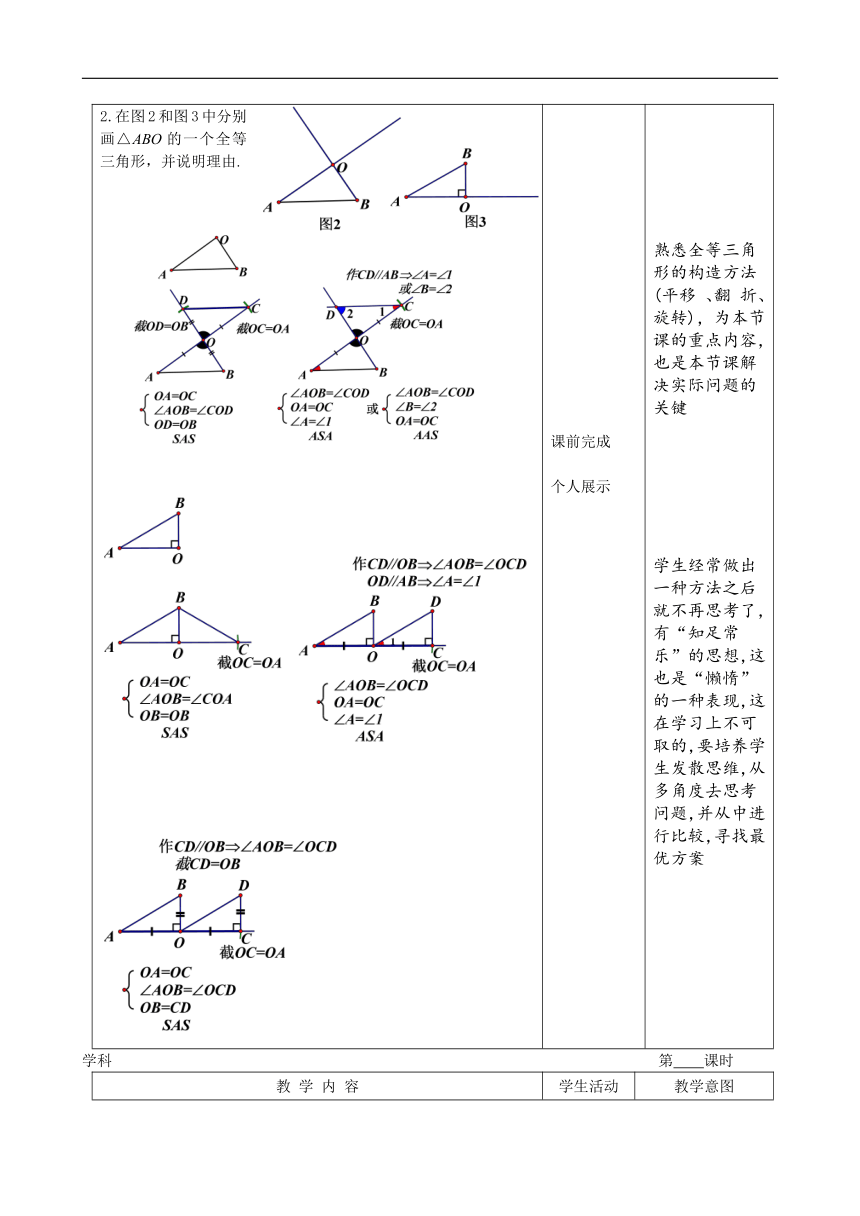
2.在图2和图3中分别画△ABO的一个全等三角形,并说明理由. 课前完成 个人展示 熟悉全等三角形的构造方法(平移 、翻 折、旋转),为本节课的重点内容,也是本节课解决实际问题的关键 学生经常做出一种方法之后就不再思考了,有“知足常乐”的思想,这也是“懒惰”的一种表现,这在学习上不可取的,要培养学生发散思维,从多角度去思考问题,并从中进行比较,寻找最优方案
学科 第 课时
教 学 内 容 学生活动 教学意图
二、小组探究 1.解决“炮楼距离”问题 在“砥砺奋进的五年”大型成就展中有一个展区是实现强军目标,建设世界一流军队,和平年代军队的作用至关重要,在民族解放的战争年代,军队更是做出了重大贡献,这是一个发生在抗日战争期间的故事:为了炸毁与我军阵地隔河相望的敌人炮楼,需要测量我军阵地到敌人炮楼的距离;由于没有任何测量工具,八路军战士为此绞尽脑汁;一位聪明的战士想出了一个巧妙的办法,成功地测出了距离而炸毁了碉堡。他是这样做的:先利用军帽使自己的视线正好落在敌人炮楼的位置;再转过身,保持刚才的视线,看目光落在什么位置;然后步测出这段距离,就是我军阵地与敌人炮楼的距离,(1)你能用全等三角形知识来解释吗? (2)你还有其他的方式吗?有几种解法? 2. 解决“池塘宽度”问题 上周末,小明和朋友们游览风景区,看到了一个美丽的池塘。他们想知道池边两点A、B之间的距离,但是只有测角仪和尺子,没有船。他们应该怎么办呢?你有几种方法? 课上完成 组内交流 小组展示 由于学生没有实际经验,他们的知识大多停留在书本上,所以通过设计给出战士的具体做法,让学生站在战士的角度,将实际问题自己抽象出几何模型,进而解决问题,同时也是给他们一个解决问题的思路,从而可以思考还可以怎样解决问题,给学生一个台阶,从而引发他们的思考 这个问题更接近学生实际,在上一个问题的基础上,可以很容易得到解决,但同时这两个问题也有不同的地方,需要学生自己去发现,进而会得到不一样的解决方案,但学生很容易局限在第一个问题当中,所以要培养学生的发散思维
学科 第 课时
教 学 内 容 学生活动 教学意图
三、小组展示 1.解决“炮楼距离”问题 思考 写出解答过程 讲解思路 展示 细心的同学会发现,战士的做法恰恰利用了我们刚才的构建全等三角形的方法,但前提是先自己找到一个三角形,也就是在实际问题中抽象出一个三角形,不共线三点即可构成三角形,首先明确要测量的对象,即可确定两个点,再确定一个点,进而通过构建全等三角形,将不可测量的对象转化为可测量的对象,从而解决问题,锻炼表达能力,树立将所遇到的问题转化为所学知识上,学有所用,同时深化对所学知识的理解 学生再结合我们开始让他们自己构建全等三角形的方法,会想到其他的三种方案
学科 第 课时
教 学 内 容 学生活动 教学意图
三、小组展示 2. 解决“池塘宽度”问题 讲解思路 展示 首先检查学生对上一问题的理解,他们能不能用上一个问题的解决思路来设计 其次学生在描述自己的方案时,他们更多的还是停留在纸面,没有考虑实际操作 再次,正是因为有第一个问题,很多学生都会局限在此,方案1——方案4都是基于这种思路进行设计的,用的都是ASA(AAS) 方案5体现了这两个问题的不同,就是第一个 问题构建三角形是只能测量一个边,用ASA(AAS)而第二个问题可以测量一个三角形中的两个边长,还可以用 SAS来解决,主要培养学生的发散思维
学科 第 课时
教 学 内 容 学生活动 教学意图
四、我的收获 1.已知三角形如何利用中点、平行线构建全等三角形 2.所学知识要用的解决实际问题,转化思想 3.知识的发展需要我们这一代的努力 五、课后作业 1.公园里有一条Z字 型道路ABCD,其中AB//CD,在AB和BC段的路边各有小石凳E和M,M恰为 BC的中点,在 AB 道路上停放着一排小汽车,从而无法直接测量 B ,E 之间的距离,你能想出解决的方法吗 请说明其中的道理. 2.一个学生要测量小口瓶下半部的内径 ,他用两根长度相 等的钢条AA‘’ 、BB‘’在中点连在一起,可活动A、B两点。使A‘、B’卡在瓶的内壁上。然后量出AB间的长度,就可测量出小口瓶下半部的内径,请说明为什么 3.如图,要测量AB的长,因为无法过河接近点A,可以在AB线外任取一点D,在A B的延长线上任取一点E。连结ED和BD,并且延长BD到G.使DG=BD;延长ED到F,A使DF=ED.连结FG.并延长FG到,使H、D、A在一直线上,则H G=AB.试证明这种测量方法的原理是正确的. 总结发言 课后完成 对所学内容进行总结,一 要养成习惯,二加深对所学内容的认识升华,三锻炼表达能力 巩固所学 加深理解
课后反思:通过这两个问题的探究学习,学生了解了全等三角形知识的实际应用,进一步理解了三角形全等的判定方法,掌握全等三角形的构造方法;同时,在思考、推理、建模、表达和转换的过程中,学生也体会到了数学说理的严谨、数学应用的价值。而从学生的反馈中也可以看到,本节课中新鲜的材料、丰富的方案激活、拓宽了学生的思维,使学生在不知不觉中感受到数学与实际的广泛、密切联系,激发出学习的兴趣和信心。 但同时我也可以看到学生在思维的发散性上,表达能力上还存在不足,在后续的教学中注意这些方面的训练。
教学课题 全等三角形的实际应用
教学目标 1.让学生进一步巩固判定三角形全等的方法,培养学生的理性思考和逻辑推理能力; 2.让学生经历构造全等三角形解决实际问题的过程,培养学生的数学建模能力和语言表达能力; 3.让学生感受数学与实际的广泛、密切联系,体会数学说理的严谨、数学应用的价值,激发学生学习的兴趣和信心.
教学方法 小组合作学习
教学重点 已知一个三角形利用中点,平行线构建一个与其全等的三角形
教学难点 从实际问题中抽象出几何模形(三角形),进而构建全等三角形
教学过程 作业展示——小组探究——小组展示——我的收获
教 学 内 容 学生活动 教学意图
一、独立完成 1.如图1所示,AC和BD相较于点O,且OA=OC 请你添加一个条件使△ABO≌△CDO,并说明理由. 已知条件:OA=OC 隐含条件:∠AOB=∠COD(对顶角) 回答问题 回忆三角形全等的判定定理—可用于间接测量长度、距离的SAS、ASA (AAS),
学科 第 课时
教 学 内 容 学生活动 教学意图
2.在图2和图3中分别画△ABO的一个全等三角形,并说明理由. 课前完成 个人展示 熟悉全等三角形的构造方法(平移 、翻 折、旋转),为本节课的重点内容,也是本节课解决实际问题的关键 学生经常做出一种方法之后就不再思考了,有“知足常乐”的思想,这也是“懒惰”的一种表现,这在学习上不可取的,要培养学生发散思维,从多角度去思考问题,并从中进行比较,寻找最优方案
学科 第 课时
教 学 内 容 学生活动 教学意图
二、小组探究 1.解决“炮楼距离”问题 在“砥砺奋进的五年”大型成就展中有一个展区是实现强军目标,建设世界一流军队,和平年代军队的作用至关重要,在民族解放的战争年代,军队更是做出了重大贡献,这是一个发生在抗日战争期间的故事:为了炸毁与我军阵地隔河相望的敌人炮楼,需要测量我军阵地到敌人炮楼的距离;由于没有任何测量工具,八路军战士为此绞尽脑汁;一位聪明的战士想出了一个巧妙的办法,成功地测出了距离而炸毁了碉堡。他是这样做的:先利用军帽使自己的视线正好落在敌人炮楼的位置;再转过身,保持刚才的视线,看目光落在什么位置;然后步测出这段距离,就是我军阵地与敌人炮楼的距离,(1)你能用全等三角形知识来解释吗? (2)你还有其他的方式吗?有几种解法? 2. 解决“池塘宽度”问题 上周末,小明和朋友们游览风景区,看到了一个美丽的池塘。他们想知道池边两点A、B之间的距离,但是只有测角仪和尺子,没有船。他们应该怎么办呢?你有几种方法? 课上完成 组内交流 小组展示 由于学生没有实际经验,他们的知识大多停留在书本上,所以通过设计给出战士的具体做法,让学生站在战士的角度,将实际问题自己抽象出几何模型,进而解决问题,同时也是给他们一个解决问题的思路,从而可以思考还可以怎样解决问题,给学生一个台阶,从而引发他们的思考 这个问题更接近学生实际,在上一个问题的基础上,可以很容易得到解决,但同时这两个问题也有不同的地方,需要学生自己去发现,进而会得到不一样的解决方案,但学生很容易局限在第一个问题当中,所以要培养学生的发散思维
学科 第 课时
教 学 内 容 学生活动 教学意图
三、小组展示 1.解决“炮楼距离”问题 思考 写出解答过程 讲解思路 展示 细心的同学会发现,战士的做法恰恰利用了我们刚才的构建全等三角形的方法,但前提是先自己找到一个三角形,也就是在实际问题中抽象出一个三角形,不共线三点即可构成三角形,首先明确要测量的对象,即可确定两个点,再确定一个点,进而通过构建全等三角形,将不可测量的对象转化为可测量的对象,从而解决问题,锻炼表达能力,树立将所遇到的问题转化为所学知识上,学有所用,同时深化对所学知识的理解 学生再结合我们开始让他们自己构建全等三角形的方法,会想到其他的三种方案
学科 第 课时
教 学 内 容 学生活动 教学意图
三、小组展示 2. 解决“池塘宽度”问题 讲解思路 展示 首先检查学生对上一问题的理解,他们能不能用上一个问题的解决思路来设计 其次学生在描述自己的方案时,他们更多的还是停留在纸面,没有考虑实际操作 再次,正是因为有第一个问题,很多学生都会局限在此,方案1——方案4都是基于这种思路进行设计的,用的都是ASA(AAS) 方案5体现了这两个问题的不同,就是第一个 问题构建三角形是只能测量一个边,用ASA(AAS)而第二个问题可以测量一个三角形中的两个边长,还可以用 SAS来解决,主要培养学生的发散思维
学科 第 课时
教 学 内 容 学生活动 教学意图
四、我的收获 1.已知三角形如何利用中点、平行线构建全等三角形 2.所学知识要用的解决实际问题,转化思想 3.知识的发展需要我们这一代的努力 五、课后作业 1.公园里有一条Z字 型道路ABCD,其中AB//CD,在AB和BC段的路边各有小石凳E和M,M恰为 BC的中点,在 AB 道路上停放着一排小汽车,从而无法直接测量 B ,E 之间的距离,你能想出解决的方法吗 请说明其中的道理. 2.一个学生要测量小口瓶下半部的内径 ,他用两根长度相 等的钢条AA‘’ 、BB‘’在中点连在一起,可活动A、B两点。使A‘、B’卡在瓶的内壁上。然后量出AB间的长度,就可测量出小口瓶下半部的内径,请说明为什么 3.如图,要测量AB的长,因为无法过河接近点A,可以在AB线外任取一点D,在A B的延长线上任取一点E。连结ED和BD,并且延长BD到G.使DG=BD;延长ED到F,A使DF=ED.连结FG.并延长FG到,使H、D、A在一直线上,则H G=AB.试证明这种测量方法的原理是正确的. 总结发言 课后完成 对所学内容进行总结,一 要养成习惯,二加深对所学内容的认识升华,三锻炼表达能力 巩固所学 加深理解
课后反思:通过这两个问题的探究学习,学生了解了全等三角形知识的实际应用,进一步理解了三角形全等的判定方法,掌握全等三角形的构造方法;同时,在思考、推理、建模、表达和转换的过程中,学生也体会到了数学说理的严谨、数学应用的价值。而从学生的反馈中也可以看到,本节课中新鲜的材料、丰富的方案激活、拓宽了学生的思维,使学生在不知不觉中感受到数学与实际的广泛、密切联系,激发出学习的兴趣和信心。 但同时我也可以看到学生在思维的发散性上,表达能力上还存在不足,在后续的教学中注意这些方面的训练。
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
