5.1.2 垂线 课件(共24张PPT)
图片预览






文档简介
(共24张PPT)
人教版 七年级下
5.1.2 垂线
一类特殊的相交关系—垂直
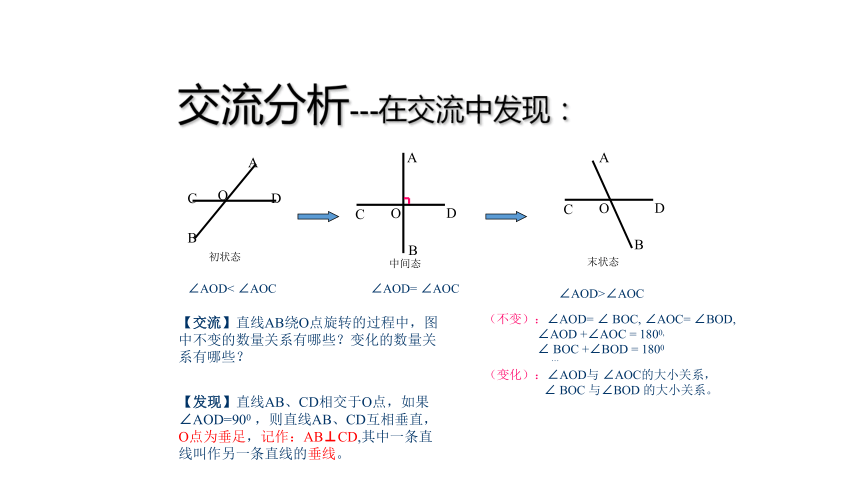
交流分析---在交流中发现:
A
B
C
D
O
中间态
A
B
C
D
O
初状态
A
B
C
D
O
末状态
【交流】直线AB绕O点旋转的过程中,图中不变的数量关系有哪些?变化的数量关系有哪些?
(不变):∠AOD= ∠ BOC, ∠AOC= ∠BOD,
∠AOD +∠AOC = 1800,
∠ BOC +∠BOD = 1800
…
(变化):∠AOD与 ∠AOC的大小关系,
∠ BOC 与∠BOD 的大小关系。
∠AOD< ∠AOC
∠AOD= ∠AOC
∠AOD>∠AOC
【发现】直线AB、CD相交于O点,如果∠AOD=900 ,则直线AB、CD互相垂直,
O点为垂足,记作:AB⊥CD,其中一条直
线叫作另一条直线的垂线。
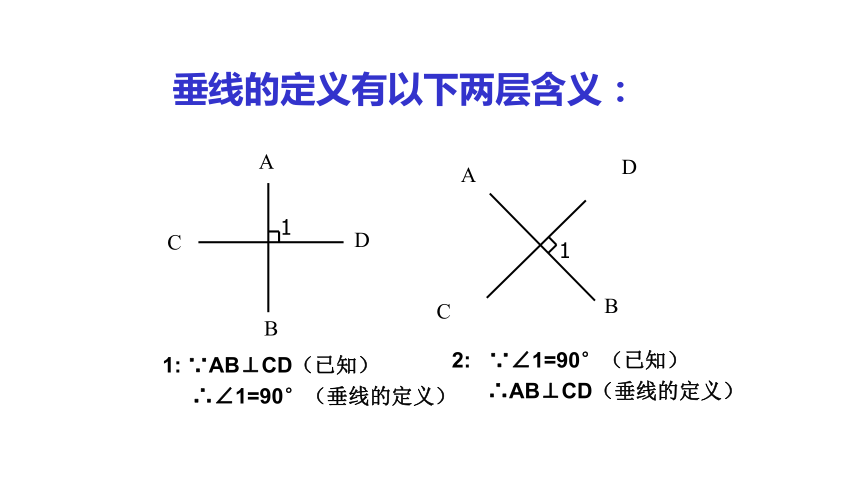
垂线的定义有以下两层含义:
A
B
C
D
1
A
B
C
D
1
1: ∵AB⊥CD(已知)
∴∠1=90°(垂线的定义)
2: ∵∠1=90°(已知)
∴AB⊥CD(垂线的定义)
生活中的垂直
活动探究---在实践中收获:
【思考】如何过一点画已知直线的垂线?
o
收获1:过直线外一点有且只有一条直线与已知直线垂直。
讨论:点与直线的位置关系。
【操作1】过直线外一点画已知
直线的垂线? 如右图
动手画一画:
活动探究---在实践中收获:
o
【操作2】过直线上一点画已知
直线的垂线? 如右图
收获2:过直线上一点有且只有一条直线与已知直线垂直。
【总结】过一点(已知直线上或已知直线外)有且只有一条直线与已知直线垂直。
你能通过折纸解决以上问题吗?
例题解读---在应用中提升:
解:
∵∠1=35°,∠2=55°(已知)
垂直( OE⊥AB )
∴ ∠AOE=180°-∠1-∠2
= 180°-35°-55°
=90°
∴OE⊥AB (垂直的定义)
例1:如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35° ∠2=55°,则OE与AB的位置关系是________________
C
D
A
B
O
E
1
2
例题解读---在应用中提升:
例2:如图 ,已知AB. CD相交于O, OE⊥CD
于O,∠AOC=36°,则∠BOE= 。
(A)36°
(B) 64°
(C)144°
(D) 54°
A
B
O
C
D
E
54°
探究:
①用三角尺或量角器画已知直线l 的垂线,这样的垂线能画出几条?
②经过直线l上一点A画 l 的垂线,这样的垂线能画出几条?
③经过直线l 外一点B画 l 的垂线,这样的垂线能画出几条?
垂线的画法
垂线的画法:
l
A
如图,已知直线 l 和l外的一点A ,作l的垂线.
B
4画线:沿着三角板的另一直角边画出垂线.
1放:放直尺,直尺的一边要与已知直线重合;
3移:移动三角板到已知点;
2靠:靠三角板,把三角板的一直角边靠在直尺上;
则所画直线AB是经过点A的直线l的垂线.
结论:过直线外一点有且只有一条直线与已知直线垂直.
垂线的性质1:
过一点有且只有一条直线与已知直线垂直.
能作一条,而且只能作一条.
问题:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条
注意:
过一点画已知线段(或射线)的垂线,
就是画这条线段(或射线)所在直线的垂线.
C
D
E
l
1.线段AB, AC, AD , AE谁最短?
2.你能概括一下这个结论吗?
如图,从A点向已知直线 l 画一条垂直的线段和几条不垂直的线段。
B
A
点到直线的距离
连接直线外一点与直线上各点的所有线段中,垂线段最短。
垂线段最短
P
A
B
C
m
D
简单说成:垂线段最短.
直线外一点到这条直线的线段的垂长度,叫做点到直线的距离。
拓 展 应 用
如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。
C
∟
垂线段最短
1 .两条直线相交所成的四个角中,下列条件中能判
定两条直线垂直的是( )
(A) 有两个角相等 ( B)有两对角相等
(C) 有三个角相等 ( D) 有四对邻补角
C
课堂练习:
2.如图, AC⊥BC, ∠C=900 ,线段AC、BC、CD中最短的是( )
(A) AC (B) BC (C) CD (D) 不能确定
D
A
B
C
C
3.过点P 向线段AB 所在直线引垂线,正确的是( ).
A B C D
C
4.如图,已知直线AB,CD都经过O点,OE为射线,若∠1=35°,∠2=55°,则OE与AB的位置关系是 .
C
A
B
O
E
1
2
OE⊥AB
垂线
概念
基本事实
点到直线的距离
直线AB与CD相交于点O,若∠AOC=90°,则AB⊥CD,点O为垂足。
经过直线上或直线外的一点,有且只有一条直线与已知直线垂直。
直线外的一点与直线上各点连接的所有线段中,垂线段最短。
垂线段CO的长度叫做点C到直线AB的距离。
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教版 七年级下
5.1.2 垂线
一类特殊的相交关系—垂直
交流分析---在交流中发现:
A
B
C
D
O
中间态
A
B
C
D
O
初状态
A
B
C
D
O
末状态
【交流】直线AB绕O点旋转的过程中,图中不变的数量关系有哪些?变化的数量关系有哪些?
(不变):∠AOD= ∠ BOC, ∠AOC= ∠BOD,
∠AOD +∠AOC = 1800,
∠ BOC +∠BOD = 1800
…
(变化):∠AOD与 ∠AOC的大小关系,
∠ BOC 与∠BOD 的大小关系。
∠AOD< ∠AOC
∠AOD= ∠AOC
∠AOD>∠AOC
【发现】直线AB、CD相交于O点,如果∠AOD=900 ,则直线AB、CD互相垂直,
O点为垂足,记作:AB⊥CD,其中一条直
线叫作另一条直线的垂线。
垂线的定义有以下两层含义:
A
B
C
D
1
A
B
C
D
1
1: ∵AB⊥CD(已知)
∴∠1=90°(垂线的定义)
2: ∵∠1=90°(已知)
∴AB⊥CD(垂线的定义)
生活中的垂直
活动探究---在实践中收获:
【思考】如何过一点画已知直线的垂线?
o
收获1:过直线外一点有且只有一条直线与已知直线垂直。
讨论:点与直线的位置关系。
【操作1】过直线外一点画已知
直线的垂线? 如右图
动手画一画:
活动探究---在实践中收获:
o
【操作2】过直线上一点画已知
直线的垂线? 如右图
收获2:过直线上一点有且只有一条直线与已知直线垂直。
【总结】过一点(已知直线上或已知直线外)有且只有一条直线与已知直线垂直。
你能通过折纸解决以上问题吗?
例题解读---在应用中提升:
解:
∵∠1=35°,∠2=55°(已知)
垂直( OE⊥AB )
∴ ∠AOE=180°-∠1-∠2
= 180°-35°-55°
=90°
∴OE⊥AB (垂直的定义)
例1:如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35° ∠2=55°,则OE与AB的位置关系是________________
C
D
A
B
O
E
1
2
例题解读---在应用中提升:
例2:如图 ,已知AB. CD相交于O, OE⊥CD
于O,∠AOC=36°,则∠BOE= 。
(A)36°
(B) 64°
(C)144°
(D) 54°
A
B
O
C
D
E
54°
探究:
①用三角尺或量角器画已知直线l 的垂线,这样的垂线能画出几条?
②经过直线l上一点A画 l 的垂线,这样的垂线能画出几条?
③经过直线l 外一点B画 l 的垂线,这样的垂线能画出几条?
垂线的画法
垂线的画法:
l
A
如图,已知直线 l 和l外的一点A ,作l的垂线.
B
4画线:沿着三角板的另一直角边画出垂线.
1放:放直尺,直尺的一边要与已知直线重合;
3移:移动三角板到已知点;
2靠:靠三角板,把三角板的一直角边靠在直尺上;
则所画直线AB是经过点A的直线l的垂线.
结论:过直线外一点有且只有一条直线与已知直线垂直.
垂线的性质1:
过一点有且只有一条直线与已知直线垂直.
能作一条,而且只能作一条.
问题:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条
注意:
过一点画已知线段(或射线)的垂线,
就是画这条线段(或射线)所在直线的垂线.
C
D
E
l
1.线段AB, AC, AD , AE谁最短?
2.你能概括一下这个结论吗?
如图,从A点向已知直线 l 画一条垂直的线段和几条不垂直的线段。
B
A
点到直线的距离
连接直线外一点与直线上各点的所有线段中,垂线段最短。
垂线段最短
P
A
B
C
m
D
简单说成:垂线段最短.
直线外一点到这条直线的线段的垂长度,叫做点到直线的距离。
拓 展 应 用
如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。
C
∟
垂线段最短
1 .两条直线相交所成的四个角中,下列条件中能判
定两条直线垂直的是( )
(A) 有两个角相等 ( B)有两对角相等
(C) 有三个角相等 ( D) 有四对邻补角
C
课堂练习:
2.如图, AC⊥BC, ∠C=900 ,线段AC、BC、CD中最短的是( )
(A) AC (B) BC (C) CD (D) 不能确定
D
A
B
C
C
3.过点P 向线段AB 所在直线引垂线,正确的是( ).
A B C D
C
4.如图,已知直线AB,CD都经过O点,OE为射线,若∠1=35°,∠2=55°,则OE与AB的位置关系是 .
C
A
B
O
E
1
2
OE⊥AB
垂线
概念
基本事实
点到直线的距离
直线AB与CD相交于点O,若∠AOC=90°,则AB⊥CD,点O为垂足。
经过直线上或直线外的一点,有且只有一条直线与已知直线垂直。
直线外的一点与直线上各点连接的所有线段中,垂线段最短。
垂线段CO的长度叫做点C到直线AB的距离。
课堂小结
https://www.21cnjy.com/help/help_extract.php
