沪科版数学七年级下册 第6章 6.1平方根、立方根课件(共21张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 第6章 6.1平方根、立方根课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 595.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 17:18:11 | ||
图片预览




文档简介
(共22张PPT)
6.1平方根
教学目的:
1、使学生理解数的平方根的概念,能运用根号表示一个数的平方;
2、掌握用平方根运算求某些数的平方根的方法。
教学重点:平方根的概念及求某些数的平方根的方法
教学难点:平方根的概念
勇攀高峰
(1)已知正方形面积是4㎝2,那么它的边长是多少?
从问题中产生新的课题:
S=4㎝2
2㎝
2㎝
2㎝
2㎝
(2)已知正方形面积是2㎝2,那么它的边长是多少?
从问题中产生新的课题:
S=2㎝2
?!
?!
?!
?!
(3)已知正方形面积是a㎝2,那么它的边长是多少?
从问题中产生新的课题:
S= a ㎝2
?!
?!
?!
?!
数的开方
新的运算:
---------乘方的逆运算
复习平方、乘方及幂:
(2)42= ,(-4)2= ;
(3) , ;
(4)(0.8)2= , (-0.8)2= 。
(1)什么叫乘方?什么叫幂?
答:求相同因数的积的运算叫做乘方;乘方的运算结果叫做幂。
16
16
0.64
0.64
显然乘方是已知底数和指数,求幂。
如: 42已知底数4及指数2,求幂16。
反过来:如果已知一个数平方等于16,怎样求这个数?即知已指数2及幂16,求底数???
解:
设这个数为x
则 x 2 =16
∵4 2 = 16,(-4)2 = 16
∴ x = 4 或 -4
因为4 、-4的平方都等于16,我们把4及-4叫做16的平方根。
同理: 的平方等于 。那么 叫 的平方根。
0.8、- 0.8的平方等于0.64。那么 叫
的平方根。
0.8、- 0.8
0.64
什么叫数的平方根???
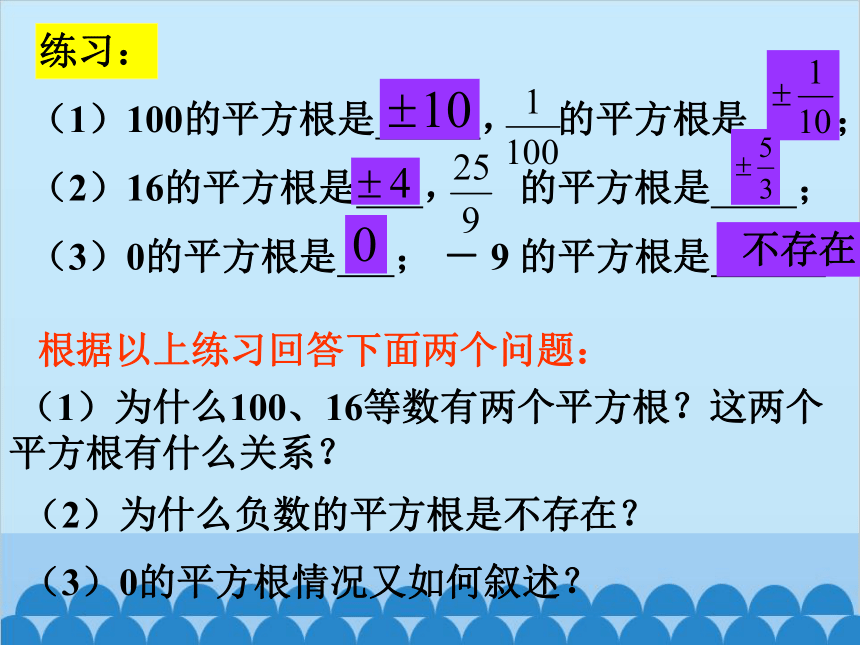
(1)100的平方根是 , 的平方根是 ;
(2)16的平方根是 , 的平方根是 ;
(3)0的平方根是 ; - 9 的平方根是 。
练习:
不存在
(1)为什么100、16等数有两个平方根?这两个平方根有什么关系?
(2)为什么负数的平方根是不存在?
根据以上练习回答下面两个问题:
(3)0的平方根情况又如何叙述?
(2)已知正方形面积是2㎝2,那么它的边长是多少?
(3)已知正方形面积是a㎝2,那么它的边长是多少?
S= a ㎝2
S=2㎝2
前面的两个问题解决了吗
一个正数a的表示方法:
(1)当a > 0时, a的正的平方根用符号“ ”表示。
根指数
被开方数
a负平方根用符号表示 “ ”
总之:正数a的平方根是 。
读作:二次根号
读作:二次根号a
读作:正负二次根号a
0;
(2)当a = 0时,
0;
一个非负数a的表示方法:
当a ≥ 0时, a的正的平方根用符号“ ”表示。
根指数
被开方数
a负平方根用符号表示 “ ”
总之:非负数a的平方根是 。
读作:二次根号
读作:二次根号a
读作:正负二次根号a
一个非负数a的表示方法:
当a ≥ 0时, a的正的平方根用符号“ ”表示。
被开方数
a负平方根用符号表示 “ ”
总之:非负数a的平方根是 。
读作:根号
读作:根号a
读作:正负根号a
如果x2=a,那么a的平方根表示为x=
例如:2的平方根记作 ,读作:
正负根号2
未解决的问题:
(1)平方根是怎样产生的?
(2)平方根的本质是什么?是一种运算方法?是一个数?。。。。。
求一个数的平方根的运算叫开平方。
开平方与平方是互为逆运算
正数与零
任何数
幂
平方根
开方
平方
运算符号
适用范围
运算结果名称
性质
正数有 个平方根,它们是 ,零的平方根是 , 负数 .
正数的平方是 数; 零的平方是 ; 负数的平方根是 数.
正
正
0
2
互为相反数
0
没有平方根
例1 求下列各数的平方根:
(1) 81 (2) (3) (4)0.49 (5)169
分析 问:解题思想方法是?
答:根据平方根的定义,把求平方根转化为求平方。即求出平方等于81的所有数。
解:
(1)∵
即
∴81的平方根是
(2)
∵
∴ 的平方根是
即
例2 下列各数有平方根吗?如果有,求出它的平方根;如果没有,请说明理由。
(1)-64 (2)0 (3)(-4)2
解:(1)因为-64是负数,所以-64没有平方根
(2)0有一个平方根,它是0;
(3)因为(-4)2=16
所以(-4)2的平方根就是16的平方根
因此的(-4)2平方根是
(1)因为 ,所以 是 的平方根;
(2) 时 , 0 ; 0 。
一、概念理解填空题:
(3)0的平方根可以理解成: ;
。
所以概括为 。
0
0
0
巩固练习:
二、选择题:
1、在0、-9、2、(-2)2 中,有平方根的是( )
A、1个 B、2个 C、3个 D、4个
2、数16的平方根是( )
A、4 B、 C、 -4 D、4或-4
3、数0.25的平方根是( )
A、0.5 B、0.05 C、-0.5 D、0.5或-0.5
4、数(-6)2的平方根是( )
A、-6 B、6 C、6或-6 D、无平方根
C
D
D
C
三、判断题:
(1)114的平方根是-12与12;
(2)256的平方根是14;
(3)256的平方根是-14;
(4)5是25的一个平方根;
(5)-5是25的一个平方根;
(6)1的平方根是1;
(7)-1的平方根是-1;
(8)-1是1的平方根;
(9)(-1)2的平方根-1。
√
×
√
√
√
×
×
×
×
小结
1、如果 ,那么 就叫做 的平方根,用 来
表示。当 时,有两个平方根,即 , 表
示 的正平方根, 表示负平方根。
2、开平方与平方
6.1平方根
教学目的:
1、使学生理解数的平方根的概念,能运用根号表示一个数的平方;
2、掌握用平方根运算求某些数的平方根的方法。
教学重点:平方根的概念及求某些数的平方根的方法
教学难点:平方根的概念
勇攀高峰
(1)已知正方形面积是4㎝2,那么它的边长是多少?
从问题中产生新的课题:
S=4㎝2
2㎝
2㎝
2㎝
2㎝
(2)已知正方形面积是2㎝2,那么它的边长是多少?
从问题中产生新的课题:
S=2㎝2
?!
?!
?!
?!
(3)已知正方形面积是a㎝2,那么它的边长是多少?
从问题中产生新的课题:
S= a ㎝2
?!
?!
?!
?!
数的开方
新的运算:
---------乘方的逆运算
复习平方、乘方及幂:
(2)42= ,(-4)2= ;
(3) , ;
(4)(0.8)2= , (-0.8)2= 。
(1)什么叫乘方?什么叫幂?
答:求相同因数的积的运算叫做乘方;乘方的运算结果叫做幂。
16
16
0.64
0.64
显然乘方是已知底数和指数,求幂。
如: 42已知底数4及指数2,求幂16。
反过来:如果已知一个数平方等于16,怎样求这个数?即知已指数2及幂16,求底数???
解:
设这个数为x
则 x 2 =16
∵4 2 = 16,(-4)2 = 16
∴ x = 4 或 -4
因为4 、-4的平方都等于16,我们把4及-4叫做16的平方根。
同理: 的平方等于 。那么 叫 的平方根。
0.8、- 0.8的平方等于0.64。那么 叫
的平方根。
0.8、- 0.8
0.64
什么叫数的平方根???
(1)100的平方根是 , 的平方根是 ;
(2)16的平方根是 , 的平方根是 ;
(3)0的平方根是 ; - 9 的平方根是 。
练习:
不存在
(1)为什么100、16等数有两个平方根?这两个平方根有什么关系?
(2)为什么负数的平方根是不存在?
根据以上练习回答下面两个问题:
(3)0的平方根情况又如何叙述?
(2)已知正方形面积是2㎝2,那么它的边长是多少?
(3)已知正方形面积是a㎝2,那么它的边长是多少?
S= a ㎝2
S=2㎝2
前面的两个问题解决了吗
一个正数a的表示方法:
(1)当a > 0时, a的正的平方根用符号“ ”表示。
根指数
被开方数
a负平方根用符号表示 “ ”
总之:正数a的平方根是 。
读作:二次根号
读作:二次根号a
读作:正负二次根号a
0;
(2)当a = 0时,
0;
一个非负数a的表示方法:
当a ≥ 0时, a的正的平方根用符号“ ”表示。
根指数
被开方数
a负平方根用符号表示 “ ”
总之:非负数a的平方根是 。
读作:二次根号
读作:二次根号a
读作:正负二次根号a
一个非负数a的表示方法:
当a ≥ 0时, a的正的平方根用符号“ ”表示。
被开方数
a负平方根用符号表示 “ ”
总之:非负数a的平方根是 。
读作:根号
读作:根号a
读作:正负根号a
如果x2=a,那么a的平方根表示为x=
例如:2的平方根记作 ,读作:
正负根号2
未解决的问题:
(1)平方根是怎样产生的?
(2)平方根的本质是什么?是一种运算方法?是一个数?。。。。。
求一个数的平方根的运算叫开平方。
开平方与平方是互为逆运算
正数与零
任何数
幂
平方根
开方
平方
运算符号
适用范围
运算结果名称
性质
正数有 个平方根,它们是 ,零的平方根是 , 负数 .
正数的平方是 数; 零的平方是 ; 负数的平方根是 数.
正
正
0
2
互为相反数
0
没有平方根
例1 求下列各数的平方根:
(1) 81 (2) (3) (4)0.49 (5)169
分析 问:解题思想方法是?
答:根据平方根的定义,把求平方根转化为求平方。即求出平方等于81的所有数。
解:
(1)∵
即
∴81的平方根是
(2)
∵
∴ 的平方根是
即
例2 下列各数有平方根吗?如果有,求出它的平方根;如果没有,请说明理由。
(1)-64 (2)0 (3)(-4)2
解:(1)因为-64是负数,所以-64没有平方根
(2)0有一个平方根,它是0;
(3)因为(-4)2=16
所以(-4)2的平方根就是16的平方根
因此的(-4)2平方根是
(1)因为 ,所以 是 的平方根;
(2) 时 , 0 ; 0 。
一、概念理解填空题:
(3)0的平方根可以理解成: ;
。
所以概括为 。
0
0
0
巩固练习:
二、选择题:
1、在0、-9、2、(-2)2 中,有平方根的是( )
A、1个 B、2个 C、3个 D、4个
2、数16的平方根是( )
A、4 B、 C、 -4 D、4或-4
3、数0.25的平方根是( )
A、0.5 B、0.05 C、-0.5 D、0.5或-0.5
4、数(-6)2的平方根是( )
A、-6 B、6 C、6或-6 D、无平方根
C
D
D
C
三、判断题:
(1)114的平方根是-12与12;
(2)256的平方根是14;
(3)256的平方根是-14;
(4)5是25的一个平方根;
(5)-5是25的一个平方根;
(6)1的平方根是1;
(7)-1的平方根是-1;
(8)-1是1的平方根;
(9)(-1)2的平方根-1。
√
×
√
√
√
×
×
×
×
小结
1、如果 ,那么 就叫做 的平方根,用 来
表示。当 时,有两个平方根,即 , 表
示 的正平方根, 表示负平方根。
2、开平方与平方
