人教版数学六年级下册 6.3 统计与概率 课件(23张PPT)
文档属性
| 名称 | 人教版数学六年级下册 6.3 统计与概率 课件(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 10:29:11 | ||
图片预览







文档简介
(共24张PPT)
六、整理与复习
统计与概率
学习目标
有关“平均数”在表示数据特征方面的特点和作用。
弄清各种统计图在描述数据方面的特点及作用,体会要根据相关数据的特点恰当地选择统计图和统计表。
探索新知
1、在小学阶段,我们学过哪些统计知识?为什么要做统计工作?
学过统计表,
还有平均数
学过条形统计图,折线统计图,扇形统计图.
日常生活和生产实践中,经常需要对一些数据进行分析、比较,这样就需要进行统计。在进行统计时,又经常要用统计表、统计图,并且常常进行平均数的计算。
1、在小学阶段,我们学过哪些统计知识?为什么要做统计工作?
探索新知
统计表:
把收集到的数据经过分类、整理后,填在一定格式的表格内,用来反映情况,说明问题,这种表格叫做统计表。
统计表一般分为单式统计表和复式统计表。
探索新知
2. 各种统计图有什么特点?适合什么情况下使用?
某小学各年级男生人数统计表
年级 合计 一年级 二年级 三年级 四年级 五年级 六年级
人数
61
33
72
95
56
58
375
某小学各年级女生人数统计表
年级 合计 一年级 二年级 三年级 四年级 五年级 六年级
人数
34
33
46
63
69
60
305
单式统计表
探索新知
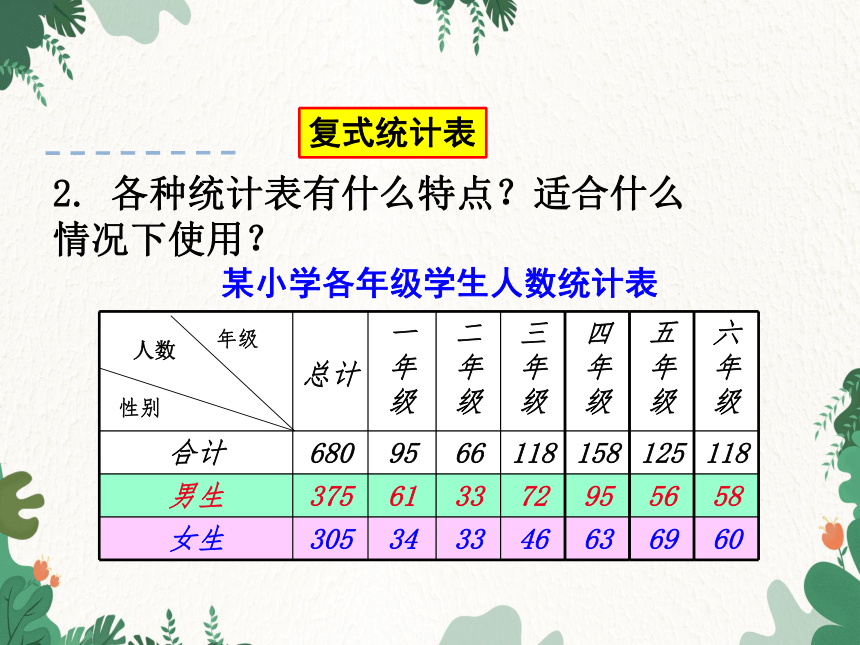
2. 各种统计表有什么特点?适合什么情况下使用?
总计 一年级 二年级 三年级
合计 680 95 66 118
男生 375 61 33 72
女生 305 34 33 46
年级
人数
性别
四年级
158
95
63
五年级
125
56
69
六年级
118
58
60
某小学各年级学生人数统计表
复式统计表
探索新知
2. 各种统计表有什么特点?适合什么情况下使用?
数据的收集和整理:
在收集数据时,通常采用画“正”字的方法比较简便。这样得到的数据叫做原始数据。
探索新知
2. 各种统计表有什么特点?适合什么情况下使用?
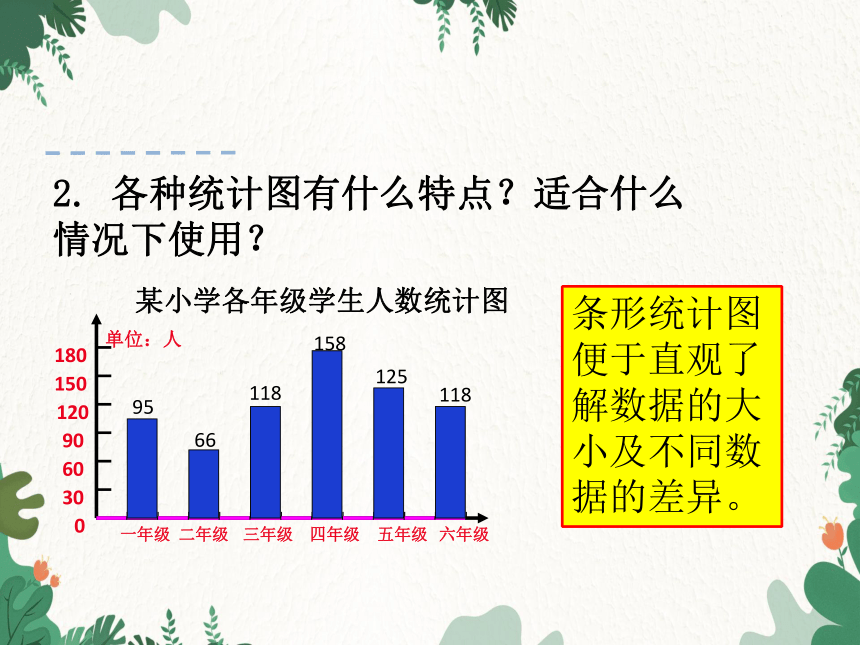
条形统计图便于直观了解数据的大小及不同数据的差异。
某小学各年级学生人数统计图
一年级
二年级
三年级
四年级
五年级
六年级
30
60
90
120
150
180
单位:人
95
66
118
158
125
118
0
探索新知
2. 各种统计图有什么特点?适合什么情况下使用?
月份
600
月产量(万元)
某陶瓷厂2004年第三、四季度各月产值统计图
7
8
9
200
400
600
800
720
540
12
11
10
470
300
350
·
·
·
·
·
·
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化的情况。
探索新知
2. 各种统计图有什么特点?适合什么情况下使用?
扇形统计图可以直观地表示出部分占整体的百分比。
其他
30%
歌曲
25%
小品
20%
杂技
15%
相声
10%
学生最喜欢的文艺节目统计图.
探索新知
2. 各种统计图有什么特点?适合什么情况下使用?
条形统计图(清楚地表示各种数量多少)
折线统计图(清楚地表示数量的变化情况)
扇形统计图(清楚地表示各种数量的占有率)
特点:
探索新知
2. 各种统计图有什么特点?适合什么情况下使用?
典题精讲
3. 数据的收集、整理和分析的步骤和方法是什
么?你能设计一张调查表,了解六年级学生的个人情况吗?
典题精讲
(1)以小组为单位,按照调查表设计的
内容分工合作,进行调查统计。
(2)想一想,除了问卷调查收集数据外,还可以通过什么手段收集数据?
实地调查、问卷调查、查阅资料、实验活动等……
①确定调查的主题及需要调查的数据;
②设计调查表或统计表;
③确定调查的方法;
④进行调查,予以记录;
⑤整理和描述数据;
⑥根据统计图表分析数据,作出判断和决策。
3.做一项调查统计工作的主要步骤:
探索新知
典题精讲
问题:1.说说你们选择这样的统计图的理由。
六(1)班男、女生人数统计表
六(1)班男 、女生人数统计图
六(1)班同学最喜欢的运动项目统计图
六(1)班同学的几项数据用统计表和统计图表示如下
根据以上统计图表,你得到哪些信息?
(1)从统计表中可以看出六(一)班男女人数及全班人数。
(2)从扇形统计图中可以知道六(一)班男女生人数各占全班人数的百分比。
(3)条形统计图表示六(一)班男生和女生最喜欢的运动项目,其中喜欢足球的男生比女生多,喜欢跳绳的女生比男生多,喜欢乒乓球的男生和女生同样多……
典题精讲
(4)折线统计图表示六(一)班同学对自己各年级时的综合表现满意人数随着年级的变化情况,其中六年级时,对自己的综合表现最满意的同学最多。
(5)从统计表中可知男生比女生多4人,从条形统计图中可知这是一个横向条形统计图,喜欢足球的男生比女生多9人,喜欢跳绳的女生是男生的3倍……
典题精讲
(1). 你看懂这个统计表中的数据了吗?请你说一说。
2. 六(1)班同学身高、体重情况如下表。
学以致用
学以致用
身高平均数:
(1.4+1.43×3+1.46×5+1.49×10+1.52×12+1.55×6+1.58×3) ÷40
=60.17 ÷40
=1.50425(m)
若干个数相加的和,除以这组数的个数所得的结果是这些数的平均数
体重平均数:
(30×2+33×4+36×5+39×12+42×10+45×4+48×3) ÷40
=1584 ÷40
=39.6(kg)
(2): 上面两组数据的平均数各是多少?说说你是怎么得到的。
学以致用
(3). 小组讨论,什么数据能代表全班同学的身高和体重?
4.如果把全班同学编号,随意抽取一名学生,该生体重在36kg及以下的可能性大?还是在39kg及以上的可能性大?为什么?
1.52能代表全班同学的身高;39KG能代表全班同学的体重
39KG以上的可能性大,因为39KG以上的人数比39KG以下的人数多。
课堂小结
统计
数据的收集和整理
统计表
统计图
单式统计表
复式统计表
条形统计图(单式和复式)
折线统计图(单式和复式)
扇形统计图
统计量
平均数
课堂小结
条形统计图:能够清楚地看出各部分数量的多少。
折线统计图:不仅能看出各部分数量的多少,还能看出数量的变化发展趋势。
扇形统计图:能够清楚地看出和部分数量同总数之间的关系。
六、整理与复习
统计与概率
学习目标
有关“平均数”在表示数据特征方面的特点和作用。
弄清各种统计图在描述数据方面的特点及作用,体会要根据相关数据的特点恰当地选择统计图和统计表。
探索新知
1、在小学阶段,我们学过哪些统计知识?为什么要做统计工作?
学过统计表,
还有平均数
学过条形统计图,折线统计图,扇形统计图.
日常生活和生产实践中,经常需要对一些数据进行分析、比较,这样就需要进行统计。在进行统计时,又经常要用统计表、统计图,并且常常进行平均数的计算。
1、在小学阶段,我们学过哪些统计知识?为什么要做统计工作?
探索新知
统计表:
把收集到的数据经过分类、整理后,填在一定格式的表格内,用来反映情况,说明问题,这种表格叫做统计表。
统计表一般分为单式统计表和复式统计表。
探索新知
2. 各种统计图有什么特点?适合什么情况下使用?
某小学各年级男生人数统计表
年级 合计 一年级 二年级 三年级 四年级 五年级 六年级
人数
61
33
72
95
56
58
375
某小学各年级女生人数统计表
年级 合计 一年级 二年级 三年级 四年级 五年级 六年级
人数
34
33
46
63
69
60
305
单式统计表
探索新知
2. 各种统计表有什么特点?适合什么情况下使用?
总计 一年级 二年级 三年级
合计 680 95 66 118
男生 375 61 33 72
女生 305 34 33 46
年级
人数
性别
四年级
158
95
63
五年级
125
56
69
六年级
118
58
60
某小学各年级学生人数统计表
复式统计表
探索新知
2. 各种统计表有什么特点?适合什么情况下使用?
数据的收集和整理:
在收集数据时,通常采用画“正”字的方法比较简便。这样得到的数据叫做原始数据。
探索新知
2. 各种统计表有什么特点?适合什么情况下使用?
条形统计图便于直观了解数据的大小及不同数据的差异。
某小学各年级学生人数统计图
一年级
二年级
三年级
四年级
五年级
六年级
30
60
90
120
150
180
单位:人
95
66
118
158
125
118
0
探索新知
2. 各种统计图有什么特点?适合什么情况下使用?
月份
600
月产量(万元)
某陶瓷厂2004年第三、四季度各月产值统计图
7
8
9
200
400
600
800
720
540
12
11
10
470
300
350
·
·
·
·
·
·
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化的情况。
探索新知
2. 各种统计图有什么特点?适合什么情况下使用?
扇形统计图可以直观地表示出部分占整体的百分比。
其他
30%
歌曲
25%
小品
20%
杂技
15%
相声
10%
学生最喜欢的文艺节目统计图.
探索新知
2. 各种统计图有什么特点?适合什么情况下使用?
条形统计图(清楚地表示各种数量多少)
折线统计图(清楚地表示数量的变化情况)
扇形统计图(清楚地表示各种数量的占有率)
特点:
探索新知
2. 各种统计图有什么特点?适合什么情况下使用?
典题精讲
3. 数据的收集、整理和分析的步骤和方法是什
么?你能设计一张调查表,了解六年级学生的个人情况吗?
典题精讲
(1)以小组为单位,按照调查表设计的
内容分工合作,进行调查统计。
(2)想一想,除了问卷调查收集数据外,还可以通过什么手段收集数据?
实地调查、问卷调查、查阅资料、实验活动等……
①确定调查的主题及需要调查的数据;
②设计调查表或统计表;
③确定调查的方法;
④进行调查,予以记录;
⑤整理和描述数据;
⑥根据统计图表分析数据,作出判断和决策。
3.做一项调查统计工作的主要步骤:
探索新知
典题精讲
问题:1.说说你们选择这样的统计图的理由。
六(1)班男、女生人数统计表
六(1)班男 、女生人数统计图
六(1)班同学最喜欢的运动项目统计图
六(1)班同学的几项数据用统计表和统计图表示如下
根据以上统计图表,你得到哪些信息?
(1)从统计表中可以看出六(一)班男女人数及全班人数。
(2)从扇形统计图中可以知道六(一)班男女生人数各占全班人数的百分比。
(3)条形统计图表示六(一)班男生和女生最喜欢的运动项目,其中喜欢足球的男生比女生多,喜欢跳绳的女生比男生多,喜欢乒乓球的男生和女生同样多……
典题精讲
(4)折线统计图表示六(一)班同学对自己各年级时的综合表现满意人数随着年级的变化情况,其中六年级时,对自己的综合表现最满意的同学最多。
(5)从统计表中可知男生比女生多4人,从条形统计图中可知这是一个横向条形统计图,喜欢足球的男生比女生多9人,喜欢跳绳的女生是男生的3倍……
典题精讲
(1). 你看懂这个统计表中的数据了吗?请你说一说。
2. 六(1)班同学身高、体重情况如下表。
学以致用
学以致用
身高平均数:
(1.4+1.43×3+1.46×5+1.49×10+1.52×12+1.55×6+1.58×3) ÷40
=60.17 ÷40
=1.50425(m)
若干个数相加的和,除以这组数的个数所得的结果是这些数的平均数
体重平均数:
(30×2+33×4+36×5+39×12+42×10+45×4+48×3) ÷40
=1584 ÷40
=39.6(kg)
(2): 上面两组数据的平均数各是多少?说说你是怎么得到的。
学以致用
(3). 小组讨论,什么数据能代表全班同学的身高和体重?
4.如果把全班同学编号,随意抽取一名学生,该生体重在36kg及以下的可能性大?还是在39kg及以上的可能性大?为什么?
1.52能代表全班同学的身高;39KG能代表全班同学的体重
39KG以上的可能性大,因为39KG以上的人数比39KG以下的人数多。
课堂小结
统计
数据的收集和整理
统计表
统计图
单式统计表
复式统计表
条形统计图(单式和复式)
折线统计图(单式和复式)
扇形统计图
统计量
平均数
课堂小结
条形统计图:能够清楚地看出各部分数量的多少。
折线统计图:不仅能看出各部分数量的多少,还能看出数量的变化发展趋势。
扇形统计图:能够清楚地看出和部分数量同总数之间的关系。
