海南省海口嘉积高级中学2021-2022学年高二下学期期中考试数学试题(Word版含答案)
文档属性
| 名称 | 海南省海口嘉积高级中学2021-2022学年高二下学期期中考试数学试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 00:00:00 | ||
图片预览



文档简介
海口嘉积高级中学2021-2022学年高二下学期期中考试
数学(B卷)
时量:120分钟 满分:150分
一、单选题(每小题5分,共8小题)
1.已知集合,则的真子集个数( )
A. B. C. D.
2.设复数满足 (为虚数的单位),在复平面内对应的点为,则( )
A. B. C. D.
3.的展开式中只有第六项的二项式系数最大,则展开式的第三项为( )
A.180 B.-180 C.180 D. -180
4.已知,则( )
A. B. C. D.
5.疫情期间,上海某医院安排5名专家到3个不同的区级医院支援,每名专家只去一个区级医院,每个区级医院至少安排一名专家,则不同的安排方法共有( )
A.60种 B.90种 C.150种 D.240种
6.已知实数,,,则的最小值是( )
A. B. C. D.
7.已知四边形中,,,,点在四边形上运动,则的最小值是
A.3 B. C. D.
8.已知函数,满足,且函数无零点,则( )
A.不等式有解 B.方程有解
C.方程有解 D.不等式有解
二、多选题(每小题5分,共4小题,漏选得2分,错选或不选得0分)
9.函数,在一个周期内的图象如图所示,则
A.函数的解析式为
B.函数的一条对称轴方程是
C.函数的对称中心是,,
D.函数是偶函数
10.等差数列的前项和为,若,公差,则( )
A.若,则 B.若,则是中最大的项
C.若, 则 D.若,则.
11.甲袋中装有4个白球,2个红球和2个黑球,乙袋中装有3个白球,3个红球和2个黑球,先从甲袋中随机取出一球放入乙袋,再从乙袋中随机取出一球,用分别表示甲袋取出的球是白球、红球和黑球,用B表示乙袋取出的球是白球,则( )
A.两两互斥 B.
C.与B是互相独立事件 D.
12.已知函数,下述结论正确的是( )
A.存在唯一极值点,且; B.存在实数,使得;
C.方程有且仅有两个实数根,且两根互为倒数
D.当时,函数与的图象有两个交点
三、填空题(每小题5分,共4小题)
13.命题的否定形式为___________.
14.若双曲线的离心率为,则实数=_________.
15.2022年北京冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”,有着可爱的外表和丰富的寓意,深受各国人民的喜爱.某商店有4个不同造型的“冰墩墩”吉祥物和3个不同造型的“雪容融”吉祥物展示在柜台上,要求“冰墩墩”和“雪容融”彼此间隔排列,则不同的排列方法种数为__________.
16.已知正三棱锥,Q为BC中点,,,则正三棱锥的外接球的半径为________;过Q的平面截三棱锥的外接球所得截面的面积范围为________.
四、解答题:(6个小题,共70份.解答应写出文字说明、证明过程或演算步骤.)
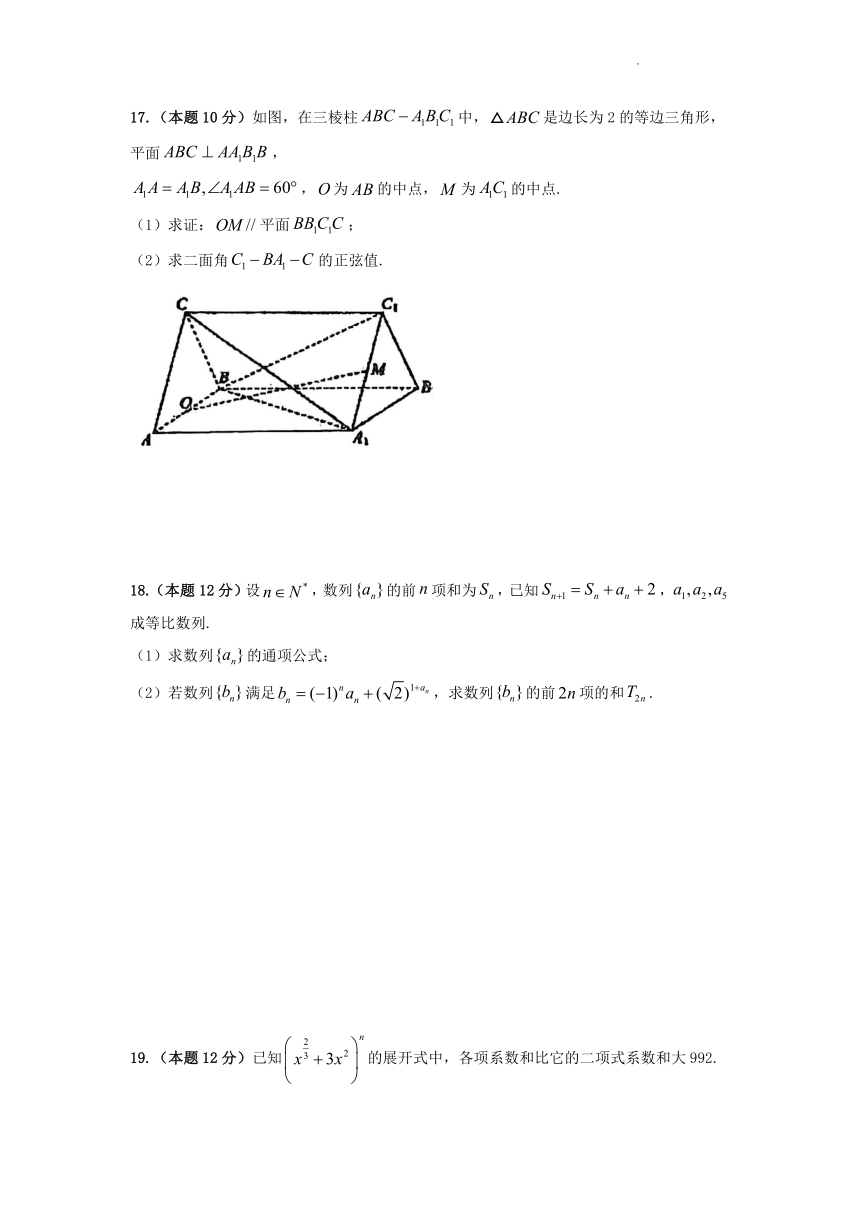
17.(本题10分)如图,在三棱柱中,是边长为2的等边三角形,平面,
,为的中点,为的中点.
(1)求证:平面;
(2)求二面角的正弦值.
18.(本题12分)设,数列的前项和为,已知,成等比数列.
(1)求数列的通项公式;
(2)若数列满足,求数列的前项的和.
19.(本题12分)已知的展开式中,各项系数和比它的二项式系数和大992.
(1)求展开式中二项式系数最大的项;
(2)求展开式中系数最大的项.
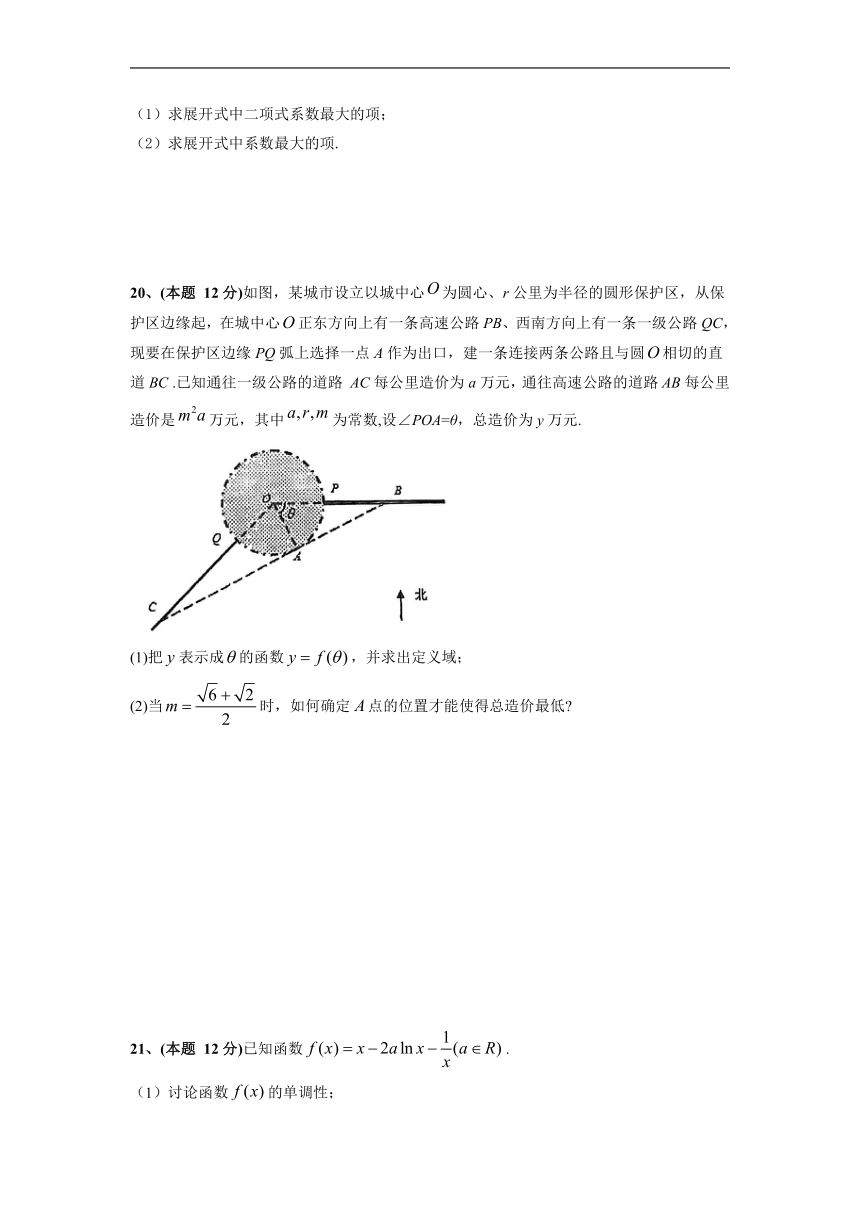
20、(本题 12分)如图,某城市设立以城中心为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆相切的直道BC .已知通往一级公路的道路 AC每公里造价为a万元,通往高速公路的道路AB每公里造价是万元,其中为常数,设∠POA=θ,总造价为y万元.
(1)把表示成的函数,并求出定义域;
(2)当时,如何确定点的位置才能使得总造价最低
21、(本题 12分)已知函数.
(1)讨论函数的单调性;
(2)若为函数的两个极值点,证明:.
22、(本题 12分)已知椭圆 的离心率为,椭圆E上的点与其右焦点F的最短距离为.
(1)求椭圆E的标准方程;
(2)若A, B, C为椭圆E上的3个动点,且△ABC的重心是,求证:△ABC的面积为定值,并求这个
定值.
海口嘉积高级中学2021-2022学年高二下学期期中考试
数学(B卷)参考答案
1.A
则的真子集为
2.B
因为.
A
的展开式中只有第六项的二项式系数最大,则最大,即.展开式的第三项为
4.D
已知,则
5、C
5名专家到3个不同的区级医院,分为1,2,2和1,1,3两种情况;
分为1,2,2时安排有;分为1,1,3时安排有
所以一共有.故选:C
6.B
∵,,
∴
当且仅当,即,时取等号.故选B
7、C
解:由题意可知,四边形是关于直线对称的图形,
故点在四边形的四条边上运动时,仅需考虑点在边,上的运动情况,
易知,所以,
①当点在边上运动时,
设则,
,
当时,取得最小值.
②当点在边上运动时,
设,则,
,
当时,取得最小值.
综上:的最小值是.故选:.
8、A
函数无零点,,
即恒成立
A. 不等式有解.恒成立,正确
B. 方程有解.恒成立,错误
C. 方程有解.设这与无零点矛盾,错误
D. 不等式有解.即,由题意:恒成立,错误
二、多选题(每小题5分,共4小题,漏选得2分,错选或不选得0分)
9.BD
解:由函数的图象知,,所以;
即,解得,所以,
由五点对应法,得,解得,所以,选项错误.
当时,,所以的一条对称轴方程是,选项正确.
令,,解得,,
所以的对称中心是,,,选项错误.
,
是定义域上的偶函数,所以选项正确.
故选:
10.BC
A错:;B对:对称轴为7;
C对:,又,;
D错:,但不能得出是否为负,因此不一定有.
故选:BC.
11.AB
对于A,由题意知不能同时发生,则两两互斥,故A正确;
对于B,由题意知,故B对;
对于C,
与B不是互相独立事件,则C错误;
对于D,由C选项可知D错误.故选:AB.
12. ACD
对进行求导可得:,显然为减函数,
,故存在,使得,
并且,,为增函数, , ,为减函数,故为极大值点,所以A正确;所以,
可得:,因为,所以,故B错
若是的一解,即,
则,
故和都是的解,故C正确,
由,可得,令,,
令 ,因为,所以,
故为减函数,而,
所以当,,即,为增函数
,,即,为减函数,
所以,故当,有两个解,故D正确.
故选:ACD
三、填空题(每小题5分,共4小题)
13、
14、2
15、根据题意,“冰墩墩”和“雪容融”彼此间隔排列,先排3个不同造型的“雪容融”,再将4个不同造型的“冰墩墩”依次安排在雪容融的空位中,有种排法,故答案为144.
16、
在正三棱锥中,取底面三角形ABC的外接圆的圆心E,则底面外接圆半径为r=AE=.
连接PE可得PE垂直面ABC,如图所示:棱锥高PE=,设外接圆O的半径为R,则,解得R=.由外接圆的半径可得球心在四棱锥的外部,过Q的平面截三棱锥P-ABC的外接球所得截面的面积最大值为过球心的大圆,所以截面面积的最大值为,最小值为过Q且与QO垂直的截面,即以BC为直径的圆,面积为.
20.
20、
21.
21、
22.
22、
数学(B卷)
时量:120分钟 满分:150分
一、单选题(每小题5分,共8小题)
1.已知集合,则的真子集个数( )
A. B. C. D.
2.设复数满足 (为虚数的单位),在复平面内对应的点为,则( )
A. B. C. D.
3.的展开式中只有第六项的二项式系数最大,则展开式的第三项为( )
A.180 B.-180 C.180 D. -180
4.已知,则( )
A. B. C. D.
5.疫情期间,上海某医院安排5名专家到3个不同的区级医院支援,每名专家只去一个区级医院,每个区级医院至少安排一名专家,则不同的安排方法共有( )
A.60种 B.90种 C.150种 D.240种
6.已知实数,,,则的最小值是( )
A. B. C. D.
7.已知四边形中,,,,点在四边形上运动,则的最小值是
A.3 B. C. D.
8.已知函数,满足,且函数无零点,则( )
A.不等式有解 B.方程有解
C.方程有解 D.不等式有解
二、多选题(每小题5分,共4小题,漏选得2分,错选或不选得0分)
9.函数,在一个周期内的图象如图所示,则
A.函数的解析式为
B.函数的一条对称轴方程是
C.函数的对称中心是,,
D.函数是偶函数
10.等差数列的前项和为,若,公差,则( )
A.若,则 B.若,则是中最大的项
C.若, 则 D.若,则.
11.甲袋中装有4个白球,2个红球和2个黑球,乙袋中装有3个白球,3个红球和2个黑球,先从甲袋中随机取出一球放入乙袋,再从乙袋中随机取出一球,用分别表示甲袋取出的球是白球、红球和黑球,用B表示乙袋取出的球是白球,则( )
A.两两互斥 B.
C.与B是互相独立事件 D.
12.已知函数,下述结论正确的是( )
A.存在唯一极值点,且; B.存在实数,使得;
C.方程有且仅有两个实数根,且两根互为倒数
D.当时,函数与的图象有两个交点
三、填空题(每小题5分,共4小题)
13.命题的否定形式为___________.
14.若双曲线的离心率为,则实数=_________.
15.2022年北京冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”,有着可爱的外表和丰富的寓意,深受各国人民的喜爱.某商店有4个不同造型的“冰墩墩”吉祥物和3个不同造型的“雪容融”吉祥物展示在柜台上,要求“冰墩墩”和“雪容融”彼此间隔排列,则不同的排列方法种数为__________.
16.已知正三棱锥,Q为BC中点,,,则正三棱锥的外接球的半径为________;过Q的平面截三棱锥的外接球所得截面的面积范围为________.
四、解答题:(6个小题,共70份.解答应写出文字说明、证明过程或演算步骤.)
17.(本题10分)如图,在三棱柱中,是边长为2的等边三角形,平面,
,为的中点,为的中点.
(1)求证:平面;
(2)求二面角的正弦值.
18.(本题12分)设,数列的前项和为,已知,成等比数列.
(1)求数列的通项公式;
(2)若数列满足,求数列的前项的和.
19.(本题12分)已知的展开式中,各项系数和比它的二项式系数和大992.
(1)求展开式中二项式系数最大的项;
(2)求展开式中系数最大的项.
20、(本题 12分)如图,某城市设立以城中心为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆相切的直道BC .已知通往一级公路的道路 AC每公里造价为a万元,通往高速公路的道路AB每公里造价是万元,其中为常数,设∠POA=θ,总造价为y万元.
(1)把表示成的函数,并求出定义域;
(2)当时,如何确定点的位置才能使得总造价最低
21、(本题 12分)已知函数.
(1)讨论函数的单调性;
(2)若为函数的两个极值点,证明:.
22、(本题 12分)已知椭圆 的离心率为,椭圆E上的点与其右焦点F的最短距离为.
(1)求椭圆E的标准方程;
(2)若A, B, C为椭圆E上的3个动点,且△ABC的重心是,求证:△ABC的面积为定值,并求这个
定值.
海口嘉积高级中学2021-2022学年高二下学期期中考试
数学(B卷)参考答案
1.A
则的真子集为
2.B
因为.
A
的展开式中只有第六项的二项式系数最大,则最大,即.展开式的第三项为
4.D
已知,则
5、C
5名专家到3个不同的区级医院,分为1,2,2和1,1,3两种情况;
分为1,2,2时安排有;分为1,1,3时安排有
所以一共有.故选:C
6.B
∵,,
∴
当且仅当,即,时取等号.故选B
7、C
解:由题意可知,四边形是关于直线对称的图形,
故点在四边形的四条边上运动时,仅需考虑点在边,上的运动情况,
易知,所以,
①当点在边上运动时,
设则,
,
当时,取得最小值.
②当点在边上运动时,
设,则,
,
当时,取得最小值.
综上:的最小值是.故选:.
8、A
函数无零点,,
即恒成立
A. 不等式有解.恒成立,正确
B. 方程有解.恒成立,错误
C. 方程有解.设这与无零点矛盾,错误
D. 不等式有解.即,由题意:恒成立,错误
二、多选题(每小题5分,共4小题,漏选得2分,错选或不选得0分)
9.BD
解:由函数的图象知,,所以;
即,解得,所以,
由五点对应法,得,解得,所以,选项错误.
当时,,所以的一条对称轴方程是,选项正确.
令,,解得,,
所以的对称中心是,,,选项错误.
,
是定义域上的偶函数,所以选项正确.
故选:
10.BC
A错:;B对:对称轴为7;
C对:,又,;
D错:,但不能得出是否为负,因此不一定有.
故选:BC.
11.AB
对于A,由题意知不能同时发生,则两两互斥,故A正确;
对于B,由题意知,故B对;
对于C,
与B不是互相独立事件,则C错误;
对于D,由C选项可知D错误.故选:AB.
12. ACD
对进行求导可得:,显然为减函数,
,故存在,使得,
并且,,为增函数, , ,为减函数,故为极大值点,所以A正确;所以,
可得:,因为,所以,故B错
若是的一解,即,
则,
故和都是的解,故C正确,
由,可得,令,,
令 ,因为,所以,
故为减函数,而,
所以当,,即,为增函数
,,即,为减函数,
所以,故当,有两个解,故D正确.
故选:ACD
三、填空题(每小题5分,共4小题)
13、
14、2
15、根据题意,“冰墩墩”和“雪容融”彼此间隔排列,先排3个不同造型的“雪容融”,再将4个不同造型的“冰墩墩”依次安排在雪容融的空位中,有种排法,故答案为144.
16、
在正三棱锥中,取底面三角形ABC的外接圆的圆心E,则底面外接圆半径为r=AE=.
连接PE可得PE垂直面ABC,如图所示:棱锥高PE=,设外接圆O的半径为R,则,解得R=.由外接圆的半径可得球心在四棱锥的外部,过Q的平面截三棱锥P-ABC的外接球所得截面的面积最大值为过球心的大圆,所以截面面积的最大值为,最小值为过Q且与QO垂直的截面,即以BC为直径的圆,面积为.
20.
20、
21.
21、
22.
22、
同课章节目录
