5.4 平移 课件 课件(共23张PPT)
文档属性
| 名称 | 5.4 平移 课件 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-24 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
人教版 七年级下
5.4 平移
如:铝合金窗户的移动,工厂里传输带上的物品,电梯上的人等。
生活中的平移现象
情景导入
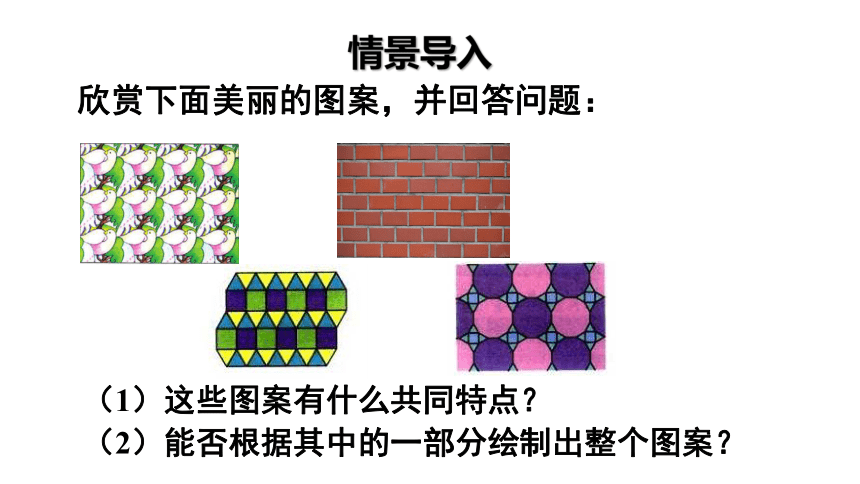
欣赏下面美丽的图案,并回答问题:
(1)这些图案有什么共同特点?
(2)能否根据其中的一部分绘制出整个图案?
知识点1
平移的概念和特征
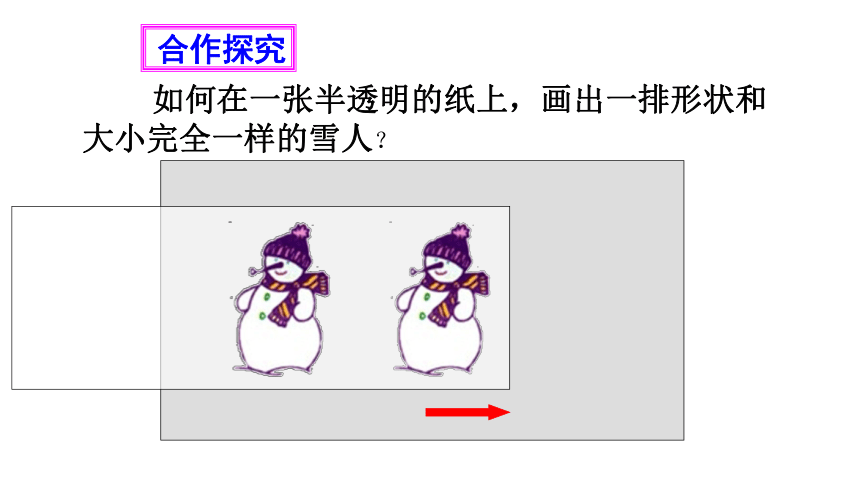
如何在一张半透明的纸上,画出一排形状和大小完全一样的雪人?
探究新知
合作探究
合作探究
如何在一张半透明的纸上,画出一排形状和大小完全一样的雪人?
荡秋千是平移吗?
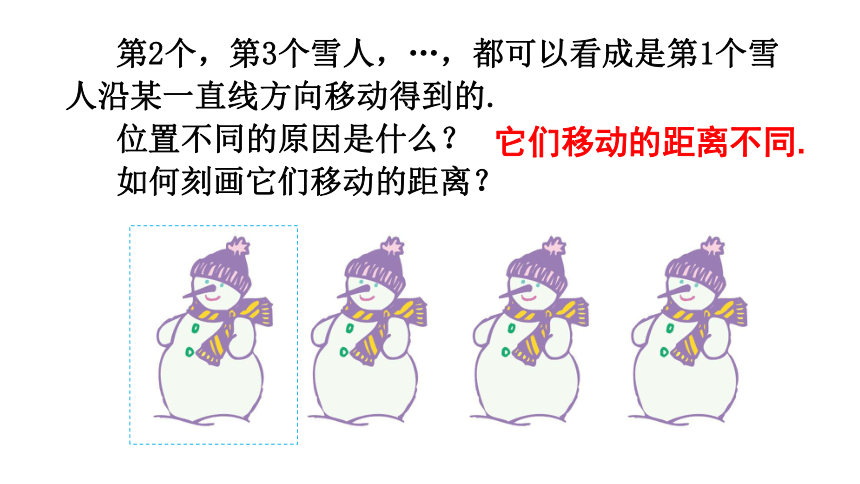
第2个,第3个雪人,…,都可以看成是第1个雪人沿某一直线方向移动得到的.
位置不同的原因是什么?
如何刻画它们移动的距离?
它们移动的距离不同.
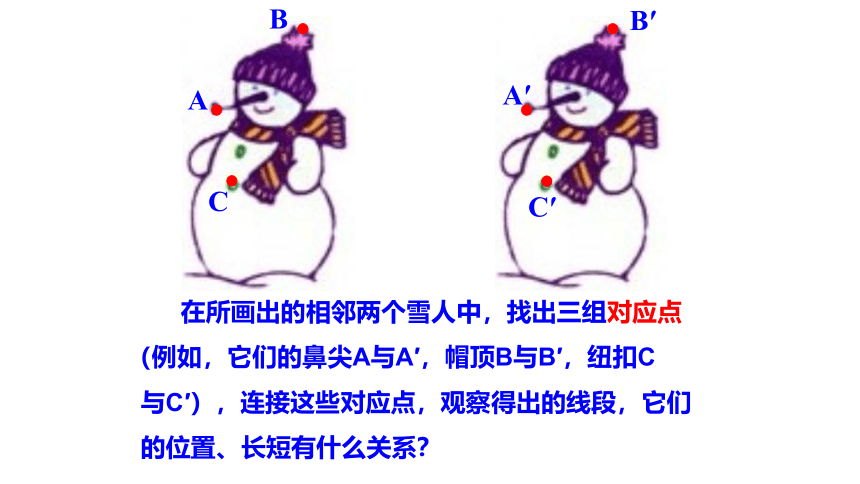
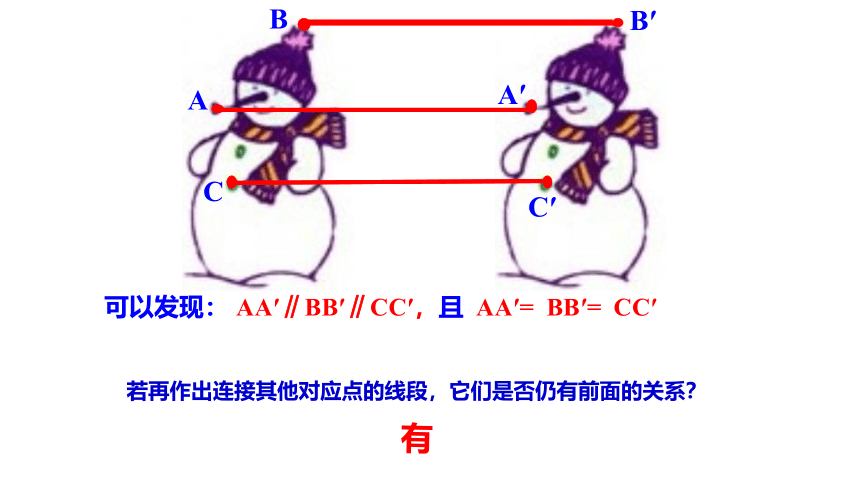
在所画出的相邻两个雪人中,找出三组对应点
(例如,它们的鼻尖A与A′,帽顶B与B′,纽扣C
与C′),连接这些对应点,观察得出的线段,它们
的位置、长短有什么关系?
B
A
C
A′
B′
C′
可以发现: AA′∥BB′∥CC′,且 AA′= BB′= CC′
若再作出连接其他对应点的线段,它们是否仍有前面的关系?
有
B
A
C
A′
B′
C′
图形平移的方向不一定是水平的;
图形平移的位置由平移的方向和距离决定.
平移作图
例1 如图,平移△ABC,使点A移动到点A',画出平移后的△A'B'C'.
B'
l
C'
解:如图,连接AA' ,过点B作的平行线l,在l 上截取BB' =AA' ,则点B'就是点B的对应点.
类似地,作出点C的对应点 C' ,得到平移后的△A'B'C'.
例2. 请在图示的方格纸上将小船向右平移4格.
错 解
如图:
正 解
如图:
练移三角形ABC,使得点A移到点A′,画出平移后的三角形A′B′C′
A
B
C
A′
B′
C′
三角形 A’B’C’ 就是三角形ABC平移后的图形.
1、如图,△ABC平移到△ DEF的位置,则:
(1)对应点:点A和______点、
点B和___点、点C和___点;
(2)对应角:∠A和____、∠B
和_______、∠ACB和_____;
(3)对应线段:线段AB和____、线段BC和____、
线段CA和____;
(4)平移方向:沿 方向平移.
(5)平移距离:线段 的长.
D
E
F
∠D
∠DEF
∠F
DE
EF
FD
射线BC
BE(CF)
A
B
E
C
F
D
随堂演练
2.如图,在一块长为a m,宽为b m的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1 m就是它的右边线,求这块草地的绿地面积.
解:绿地面积为(a-1)b=(ab-b)m2.
3、怎样用平移的方法说明平行四边形
的面积 S=ah?
a
h
平移的性质
(1)把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
(2)新图形中的每一个点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行(或在同一条直线上)且相等.
平移要注意:
平移的方向
平移的距离
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教版 七年级下
5.4 平移
如:铝合金窗户的移动,工厂里传输带上的物品,电梯上的人等。
生活中的平移现象
情景导入
欣赏下面美丽的图案,并回答问题:
(1)这些图案有什么共同特点?
(2)能否根据其中的一部分绘制出整个图案?
知识点1
平移的概念和特征
如何在一张半透明的纸上,画出一排形状和大小完全一样的雪人?
探究新知
合作探究
合作探究
如何在一张半透明的纸上,画出一排形状和大小完全一样的雪人?
荡秋千是平移吗?
第2个,第3个雪人,…,都可以看成是第1个雪人沿某一直线方向移动得到的.
位置不同的原因是什么?
如何刻画它们移动的距离?
它们移动的距离不同.
在所画出的相邻两个雪人中,找出三组对应点
(例如,它们的鼻尖A与A′,帽顶B与B′,纽扣C
与C′),连接这些对应点,观察得出的线段,它们
的位置、长短有什么关系?
B
A
C
A′
B′
C′
可以发现: AA′∥BB′∥CC′,且 AA′= BB′= CC′
若再作出连接其他对应点的线段,它们是否仍有前面的关系?
有
B
A
C
A′
B′
C′
图形平移的方向不一定是水平的;
图形平移的位置由平移的方向和距离决定.
平移作图
例1 如图,平移△ABC,使点A移动到点A',画出平移后的△A'B'C'.
B'
l
C'
解:如图,连接AA' ,过点B作的平行线l,在l 上截取BB' =AA' ,则点B'就是点B的对应点.
类似地,作出点C的对应点 C' ,得到平移后的△A'B'C'.
例2. 请在图示的方格纸上将小船向右平移4格.
错 解
如图:
正 解
如图:
练移三角形ABC,使得点A移到点A′,画出平移后的三角形A′B′C′
A
B
C
A′
B′
C′
三角形 A’B’C’ 就是三角形ABC平移后的图形.
1、如图,△ABC平移到△ DEF的位置,则:
(1)对应点:点A和______点、
点B和___点、点C和___点;
(2)对应角:∠A和____、∠B
和_______、∠ACB和_____;
(3)对应线段:线段AB和____、线段BC和____、
线段CA和____;
(4)平移方向:沿 方向平移.
(5)平移距离:线段 的长.
D
E
F
∠D
∠DEF
∠F
DE
EF
FD
射线BC
BE(CF)
A
B
E
C
F
D
随堂演练
2.如图,在一块长为a m,宽为b m的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1 m就是它的右边线,求这块草地的绿地面积.
解:绿地面积为(a-1)b=(ab-b)m2.
3、怎样用平移的方法说明平行四边形
的面积 S=ah?
a
h
平移的性质
(1)把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
(2)新图形中的每一个点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行(或在同一条直线上)且相等.
平移要注意:
平移的方向
平移的距离
课堂小结
https://www.21cnjy.com/help/help_extract.php
